‘S’型加减速曲线在机器人轨迹插补算法中的应用研究

刘鹏飞，杨孟兴，宋 科，段晓妮

（中国航天科技集团 第16研究所，西安 710100）

0 引言

工业机器人在一些应用领域如焊接和喷涂等需要对末端执行器运动的轨迹进行严格控制，这种控制称CP控制(Continuous Path Control)[1]，需要在笛卡尔空间内进行轨迹插补。用示教或离线编程的方式告诉机器人路径中的若干点，以及各点之间所走的路径是直线和圆弧等，控制器根据插补算法自动生成路径上的中间点，机器人运行后自动重复上述的路径。

轨迹插补不仅是对位置的插补，也是对速度和加速度的插补[2]。不但要求插补点的位置严格在规定路径上，而且要求末端执行器的速度连续变化，在精度速度要求更高的场合要求加速度也是连续变化的。

1 笛卡尔空间插补概念

1.1 位姿描述

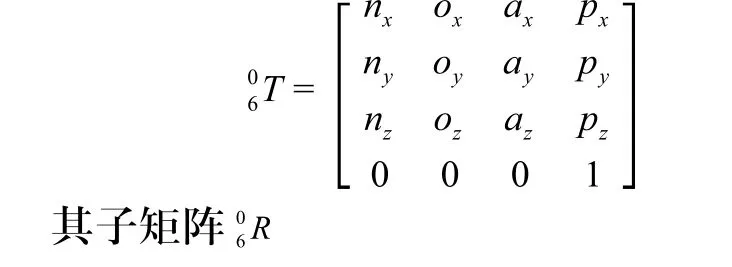
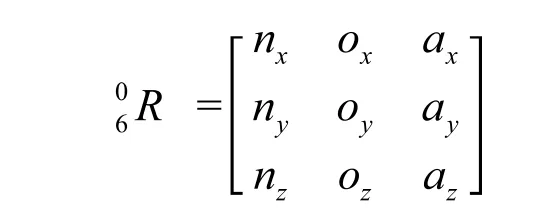
通常，用姿态角（回转、俯仰、偏转）[2]、欧拉角、等效旋转矢量和四元素这四种方式描述姿态，这四种表示方法是等效的，它们和姿态旋转矩阵之间转换方法参考文献[2]。本文用位置矢量和姿态四元数的组合描述位姿：

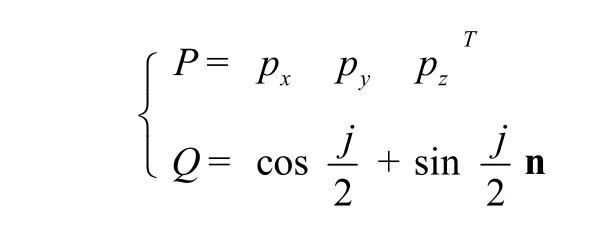
为了避免与机器人机械产生共振，插补周期应控制1-5ms以内[4]。在每个插补周期内计算机需完成一次插补运算和一次运动学逆解，计算机的计算速度有限，应尽量减少插补运算的计算量。

1.2 笛卡尔空间插补标准算法

笛卡尔空间插补算法的思路较简单，文献[3]给出了标准算法并将其应用于直线插补。

Dt是插补周期；F(t)是位姿关于时间的函数；j(t)是机器人关节坐标，由F(t)逆解得到。

计算位姿函数F(t)和逆解得到j(t)是每个插补周期内的主要工作，插补算法讨论如何获得位姿函数F(t)。机器人末端执行器在时间T内从位姿F0运动到位姿F1，其中位置从P0运动到P1，姿态旋转矩阵从R0运动到R1，选择归一化时间算子[1,3,5]l(t)=实现直线均匀插补步骤如下：

1）将姿态旋转矩阵R0和R1转换为四元数Q0和Q1表示姿态；

2）计算位置函数，P(t)=P0+l(t)×(P1P0)；

3）计算姿态四元数函数，采用两四元数的‘球形线性插补法’(spherical linear interpolation)[6]:

式中 ，q=arccos(Q1×Q2)，Q1×Q2是两个四元数的点积；

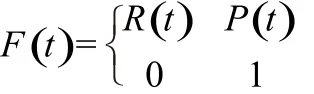
均匀插补生成的位置函数是有缺陷的：在端点P(0)处，速度由零突变为稳定值，P(T )处又由突变为零，也就是在两端点处加速度出现脉冲。这样的轨迹显然是不可取的，一方面，在机器人的启动和停止时刻会产生巨大的惯性力、向心力和哥氏力，关节上的电机无法补偿如此大的力，导致电机电流过载；另一方面，机械上会产生震动和噪声，磨损加剧影响机器人的工作寿命。

本文提出用‘S’型加减速曲线保证末端执行器的速度光滑和加速度连续。

2 ‘S’型加减速曲线

2.1 归一化时间算子分析

首先对归一化时间算子l(t)进行简要分析。l(t)有如下要求：l(0)=0，l(T )=1，t[0,T]则l(t)[0,1]且单调递增。它在插补运算中起到了调整步长的作用：若在时间T内从P0运动到P1，等时间插入N-1个中间位置，则步长为：

从上式可以看出l(t)的变化规律决定插补步长。位置函数的n阶导数为：

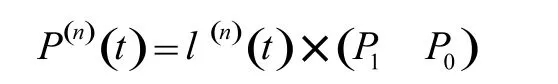
可见l(t)决定了P(t)的变化趋势。例如上文选择了一次函数作为归一化时间算子，则P(t)也以一次线性规律变化，导致加速度在直线端点是脉冲。于是考虑寻求更平滑的归一化时间算子以满足速度光滑的要求。文献[4]中提出了用抛物线拟合方法归一化时间算子，避免了加速度在起始和终止是脉冲的情况，但速度仍然是不平滑的，加速度仍然有突变。文献[7]用一段一次函数、两段一次函数与正弦函数的线性组合做归一化时间算子，解决的速度光滑的要求。本文提出用S型加减速曲线构造归一化时间算子l(t)也能满足上述要求，与文献[7]所提方法相比，减少了两个正弦函数的计算量。

2.2 S型加减速曲线

S型曲线加减速的称法是由系统在加减速阶段的速度曲线形状呈S型而来的[8,9]，广泛应用于高精度、高效率的柔性加工系统，如CNC系统。S型曲线加减速控制是指在加减速时，使其加加速度J(Jerk)为常数，通过对J持续时间长短的控制来产生平滑变化曲线，以减小对机械的冲击。整个运动分为七段：加加速段(T1)、匀加速段(T2)、减加速段(T3)、匀速段(T4)、加减速段(T5)、匀减速段(T6)、减减速段(T7)，如图1所示。

图1 S型加减速曲线

下面对其各阶段解析表达式进行分析，设：ti(i=0,1,7)为各阶段的局部时间坐标，Ti(i=0,1,7)为各阶段的运行时间如图1所示。对每段加加速度积分可以得到加速度：

上式中J为加加速度，其大小为常值； A为最大加速度；D为最大减速度。对每个阶段的加速度积分得到速度：

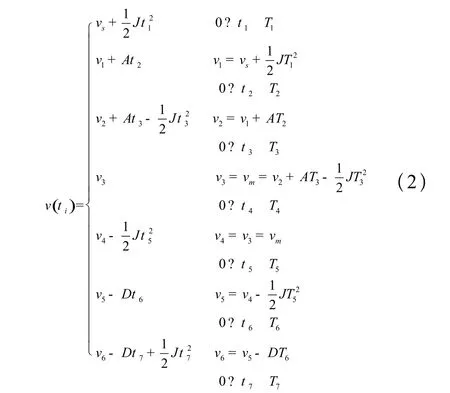
上式中vs为起始速度，vm为匀加速阶段的速度，ve为终止时的速度。对每个阶段的速度积分得到位移：

式中，si(i=0,1,2,6)为阶段i到达的总位移，s0是初始时刻的位移，通常为0。

2.3 S型加减速曲线的初始化及归一化

在插补程序执行前要定义初始位置P0、终止位置P1、初始速度vs、终止速度ve、中间速度vm、最大加速度A、最大减速度D、运行时间T。

应用初始值求解各阶段的运行时间Ti(i=0,1,7)和加速度J。加速度从0达到最大值和从最大值降到0时间相等则有：

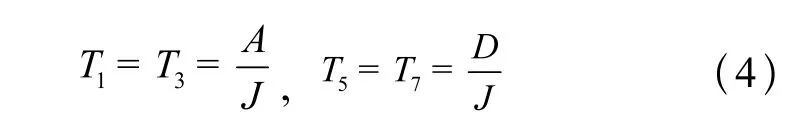
第三个阶段（减加速阶段T3）结束时达到中间速度vm，则：

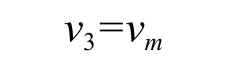
将T1和T3表达式带入式(2)并结合上式化简得：

同理有v7=ve，将T5和T7表达式带入式(2)并结合前式化简得：

运行总时间为T，解得T4：

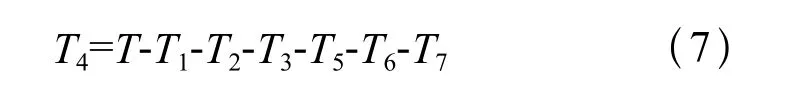
机器人末端走过的路径长度为：

根据位移公式(3)有：

将 L、vs、vm、ve、A、D 和 T1～T7表达式带入式 (7)可解得加加速度J并化简得：

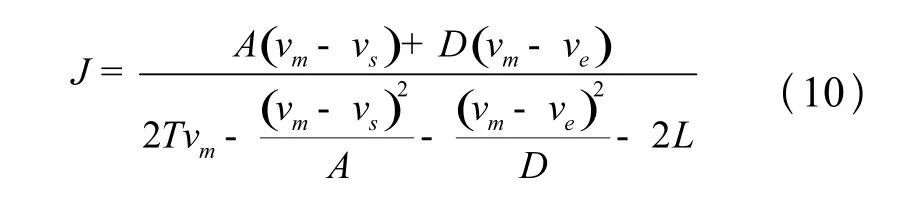
将J带入式(4)～式(7)即可求得T1～T7。

至此，将J和T1～T7带入式(1)～(3)便得到S型速度曲线的加速度a(t)、速度v(t)和位置s(t)的解析式。

把S型加减速曲线应用于笛卡尔空间轨迹插补前还需要进行归一化处理，使之满足“ l(0)=0，l(T )=1，[0,T]则l(t)[0,1]且单调递增”这三点要求。

定义归一化时间算子：

其中，s(t)为式(3)中的位置在全局时间坐标下的函数，L为式(8)或(9)中机器人末端经过的距离。

3 空间直线插补和圆弧插补

3.1 空间直线插补

直线插补是已知直线始末两点的位置和姿态，求轨迹中间点（插补点）的位置和姿态[5]。机器人末端执行器在时间T内从位姿F0运动到位姿F1，其中位置从P0运动到P1，姿态旋转矩阵从R0运动到R1。采用等时插补[10]，即在插补时间T内均匀插入N-1个点将T均匀分为N段，插补周期用式(8)计算直线两点间距离L并带入式(11)中的S型加减速曲线构造的归一化时间算子，应用1.2节所述插补算法实现空间直线插补，不在赘述。

3.2 空间圆弧插补

已知空间三点位姿F1、F2、F3，位置分别为P1、P2、P3，姿态分别为 R1、R2、R3。若 P1、P2、P3这三点不共线，则存在经过这三点的圆弧。

圆弧插补的位置插补和姿态插补需分开讨论，首先讨论位置插补。根据文献[11,12]中算法求得圆心P0的坐标、圆弧半径r和圆心角q1；在P1、P2、P3所在平面M上建立以P0为原点的新坐标系{O0}如图2所示，方向为X0轴，平面法线方向为Z0轴方向，右手定则确定Y0轴方向，文献给出了由坐标系{O0}到基坐标系{O}的齐次变换矩阵T。

图2 圆弧插补空间坐标关系示意图

圆弧位置插补步骤如下：

1）根据文献计算圆心P0、半径r、齐次变换阵T、圆心角q1；

2）以弧长rq1作为式(10)中的位移L，计算归一化函数l(t)；

4）将Pt(t)从坐标系{O0}映射到基坐标系{O}内：

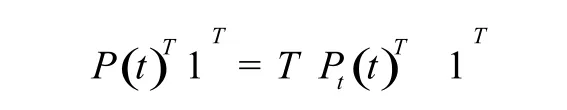
其中，T是坐标系{O0}到基坐标系{O}的齐次变换矩阵。

下面讨论姿态插补。圆弧插补对姿态的要求较弱，一般采用线性插值方式，即把末端执行器在曲线上的终点和起点的之间的姿态均匀的分配到每个插补点上[13]。为了避免在端点处仍存在的加速度突变的问题，本文仍用S型加减速曲线构造归一化时间算子l(t)将姿态平滑插补。

已知F0、F2的姿态分别为R0、R2，则姿态插补步骤如下：

1）将姿态旋转矩阵R0、R2转换为四元数Q0、Q2描述姿态；

式中，q=arccos(Q0×Q2)，Q0×Q2是两个四元数的点积；

3）将四元数Q(t)变换为姿态旋转矩阵R(t)；

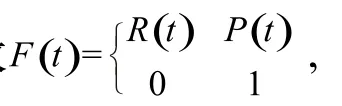
4 仿真结果与分析

4.1 直线插补仿真

直线两端点位姿为：

初始化参数如下：起点速度和终点速度都为0，中间速度为160mm/s，最大加速度和最大减速度都为58mm/s2，插补时间12s，插补周期2ms。仿真得到轨迹如图3所示，第一行为机器人末端在笛卡尔空间内经过的路径，第二行为机器人末端的位置坐标随时间的变化规律，第三行为机器人末端的速度坐标随时间的变化规律。从图中看出三个速度分量都以S型加减速规律变化，证明了算法的可行性。这个速度向量的模具有物理含义——沿着示教直线方向速度的大小，该速度也必然呈现‘S’型加减速变化规律。

图3 直线插补的轨迹位置及速度

F0和F1两点的姿态用四元数表示分别为：

Q0=(0 i 0j 0k)、Q1=(0.46837-0.85542i-0.21829j-0.3524k)为了更直观的显示由Q0到Q1的姿态插补轨迹，将四元数转换为方位角（绕X-Y-Z固定角坐标系的旋转角）表示如图4所示，图中g、b、a分别是绕X、Y、Z是转角，从图中可以看出姿态的变化也是连续平滑的。

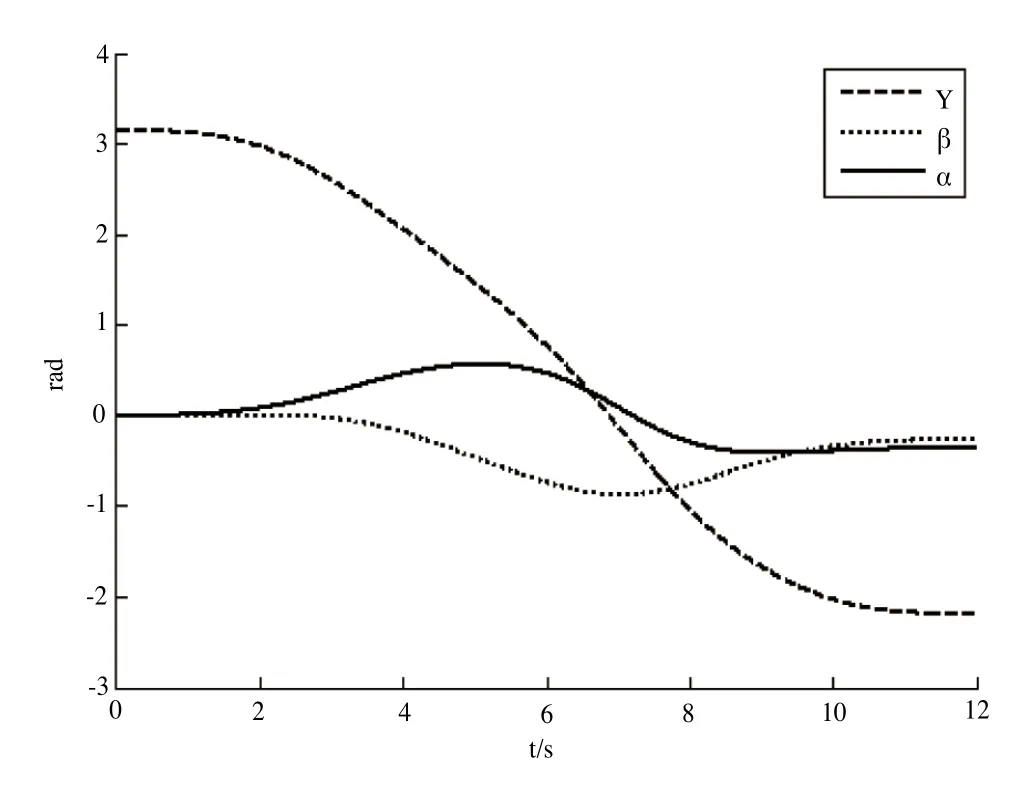
图4 直线插补的姿态

4.2 圆弧插补仿真

同理进行圆弧插补仿真，空间不共线的三点位姿为：

初始化参数如下：起点速度和终点速度都为0，中间速度为220mm/s，最大加速度和最大减速度都为58mm/s2，插补时间12s，插补周期2ms。

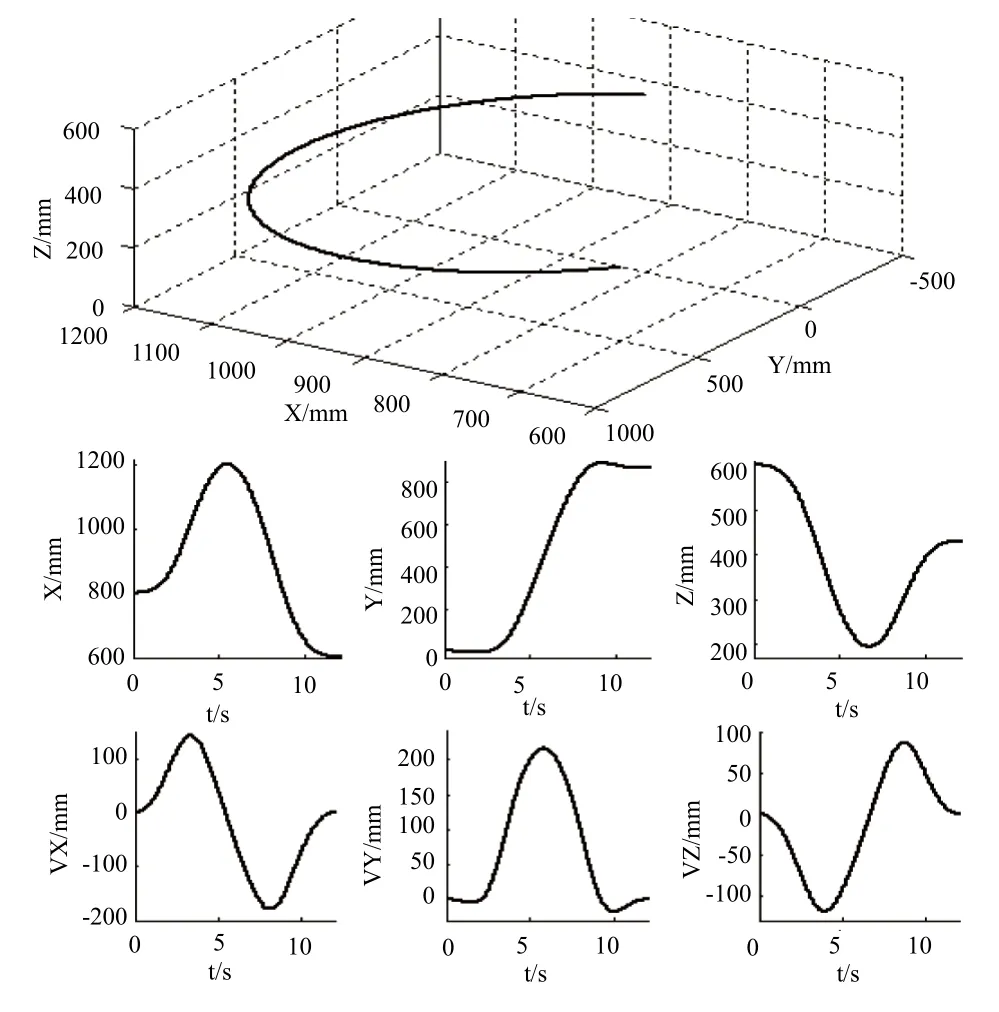
图5 圆弧插补的轨迹位置及速度

仿真得到轨迹如图5所示，第一行为机器人末端在笛卡尔空间内经过的路径，第二行为机器人末端的位置坐标随时间的变化规律，第三行为机器人末端的速度坐标随时间的变化规律。速度向量的模是沿着圆弧切线方向速度的大小，其轨迹如图6所示。从图中可以看出切线方向速度也是呈‘S’型加减速规律变化，起始速度和终点速度都为0，中间速度为220mm/s，与初始化的速度值一致，验证了算法的正确性。图7为圆弧插补的姿态曲线，图中g、b、a分别是绕X、Y、Z是转角。从图5和图7中可以看出位置及姿态的变化是连续平滑。

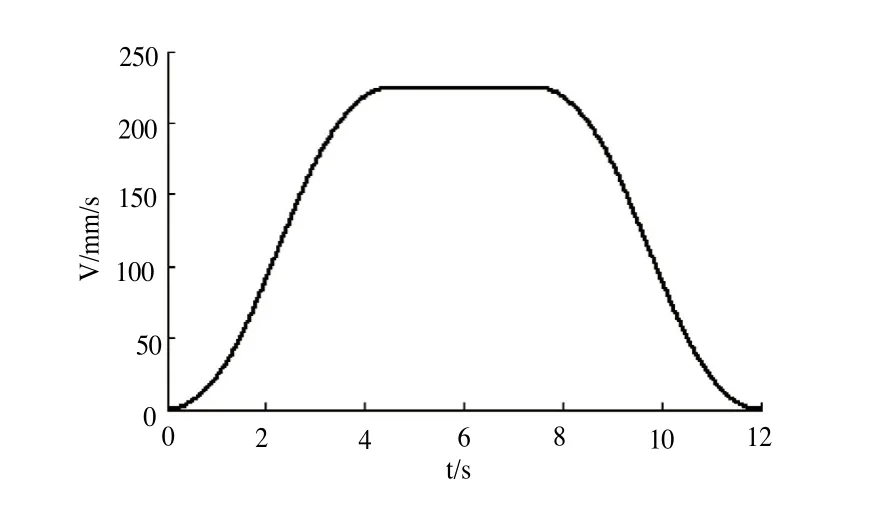
图6 圆弧切线方向速度

图7 圆弧插补的姿态

5 结束语

本文创新点在于将高速、高精度柔性加工系统中常用的‘S’型加减速曲线应用在了机器人笛卡尔空间插补算法中，对位置和姿态都进行了插补，使机器人的运动连续平滑，该方法能有效的减少系统在启动及停止时对电机和机械结构的冲击，能提高伺服精度，具有一定的实用价值。

不足之处：1）圆弧的姿态插补只通过了起始姿态R0和终止姿态R2，没有通过中间姿态R1；2）两段示教轨迹的平滑衔接需要做进一步深入研究。

[1]蔡自兴.机器人学[M].第三版.北京: 清华大学出版社,2009.

[2]John J.Craig.Introduction to Robotics-Mechanics and Control (Third Edition) [M].Upper Saddle River, New Jersey: Pearson Education, Inc., 2005.

[3]R.Taylor.Planning and Execution of Straight Line Manipulator Trajectories [J].Robot Motion, Brady et al.Editors, MIT Press, Cambridge, MA, 1983: 424-436.

[4]日本机器人学会编, 宗光华等译.机器人技术手册[M].北京: 科学出版社, 1996: 499-501.

[5]陈伟华, 张铁.六自由度喷涂机器人插补算法研究[J].微计算机信息, 2009年第25卷3-2期: 251-252

[6]K.Shoemake.Animating rotation with quaternion curves[J].Process dings of ACM SIGGRAPH, (San Francisco),the Singer Company, Link Flight Simulator Division,1985: 245-254.

[7]TAN Guanzheng, WANG Yuechao.Theoretical and experiment and research on time-optional trajectory Planning and control of industrial robots [J].Chinese Journals of Control & Application.2003.20(2): 1138-1142.

[8]黄艳, 李家雯, 于东, 等.CNC系统S型曲线加减速算法设计与实现[J].制造技术与机床, 2005, 3: 55-59.

[9]石川, 赵彤, 叶佩青, 等.数控系统S曲线加减速规划研究[J].中国机械工程, 2007, 18(12): 1421-1425.

[10]刘极峰, 易际明.机器人技术基础[M].北京: 高等教育出版社, 2006.

[11]陈国良, 黄心汉, 王敏.机械手圆周运动的轨迹规划与实现[J].华中科技大学学报(自然科学版), 33(11): 63-66.

[12]吴剑波.多轴运动控制器的PCI驱动研究及其在工业机器人中的应用[D].杭州: 浙江大学, 2010.

[13]卓扬娃, 白晓灿, 陈永明.机器人的三种规则曲线插补算法[J].装备制造技术, 2009, 11: 27-29.