基于信息融合和卡尔曼滤波的移动机器人定位技术

张国丽

（河北软件职业技术学院，保定 071000）

0 引言

近年来移动机器人的研究及相关技术应用得到了前所未有的发展。世界各地投入相当可观的财力和人力，研究各种不同的功能及应用领域的机器人。国外机器人的研究起步较早，相关技术较为成熟，所研发出来的机器人，也被应用在不同领域上，包括日常生活中的机器狗，以及用于太空的环境探测机器人。虽然国内机器人的研究成果不如国外丰硕，但许多产、学界也正努力的研发许多不同功能的机器人，取得了相当可观的成绩。

避障、导航和路径规划是移动机器人领域的三个研究热点。在移动机器人自动导航中，对未知环境中特别是一些动态环境下的环境辨识和自身的地位是当前亟待解决的一个问题。定位技术能够获得在任何时刻移动机器人的相对位置，因此是实现导航和保证机器人自主导航的关键，充分体现了机器人的自主智能能力[1]。

基于航位推算的位置估计方法是一种传统的简单定位方法。里程计信息记录了机器人的运动信息，可以通过航位推算来估计机器人的位置。但是因为移动机器人的轮子存在随机滑动，里程计存在漂移误差，移动机器人的真实运动模型不理想等原因，关于机器人的位置估计存在很大的误差。随着时间的增加，这种误差也会累计到很大。目前已经发展出来很多定位算法，如基于环境模型的定位方法、位姿跟踪方法、三角定位和概率定位方法等。其中，概率定位方法是目前定位方法中比较系统和流行的方法，它在贝叶斯规则下，通过不断更新姿态空间与位置空间的概率分布实现定位。卡尔曼滤波是一种典型的概率定位方法。

尽管卡尔曼滤波是移动机器人自主定位的首选方法之一，它主要是以线性状态模块和测量模块为基础，但实际中许多的物理系统常常是用非线性系统方程式来描述。为了提高这种情况下的定位精度。为了提高这种情况下的定位精度，本论文提出一种基于多平台下传感器融合的移动机器人精确定位技术。将多个传感器得到的距离参数，借助于卡尔曼滤波来进行定位。既可以采用多个状态变量的融合策略，又可以采用观测变量融合的策略。数值模拟结果显示，相比融合前，该方法能够获得更加精确的定位。

1 卡尔曼滤波定位

自从R.E.Kalman 在1960年提出卡尔曼滤波(Kalman Filter, KF)以来，卡尔曼滤波器已经成功的应用在许多工程问题上，例如：信号处理和目标追踪等问题。卡尔曼滤波器之所以能被应用在工程问题上，主要是因为其他运动估测方法必须储存观测系统的运算和滤波器的系数，这样将增加系统运算的复杂性。然而，卡尔曼滤波器采取的是递归的计算方式，并且使用状态空间表示法可以获得目标在不同时间的系统状态，使得计算更为简单有效。因此卡尔曼滤波定位在移动机器人自主定位中得到成功的应用[2～4]。

移动机器人的定位问题本质上是一个随机统计系统中的状态估计问题。如果该系统中的观测噪声满足高斯白噪声分布，卡尔曼滤波能够对融合的数据给出最大似然意义上的最佳估计。令X(t)=[x(k), y(k), θ(k)]表示机器人的站姿，其中θ(k)表示第k个时刻全局坐标系x轴方向与移动机器人的x轴方向之间的夹角，x(k), y(k)表示全局坐标系中第k个时刻移动机器人的坐标位置。假设k时刻机器人的位置可以利用下面的线性模型来表示：

其中，Φ(k k-1)为状态转移矩阵，U(k)为输入的控制向量，W(k)为影响U(k)的噪声向量。接下来将机器人的位置作为观测变量，建立卡尔曼滤波算法中的测量方程：其中，H(k)是观测矩阵，V(k)是观测噪声。一个基本的卡尔曼滤波过程包括如下步骤。

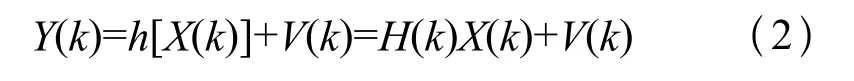
步骤1：首先按照式(3)执行系统状态的一步预测估计：

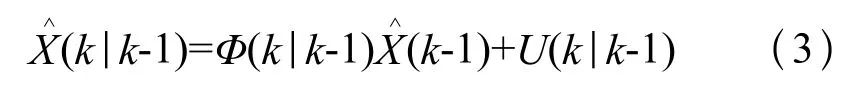
步骤2：系统状态估计：

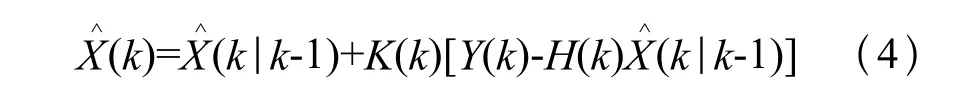
Q(k)为系统噪声协方差阵。一步预测均方误差阵P(k k-1)是从估计均方误差阵P(k-1)转移过来的，并加上了系统噪声方差的影响。步骤4：滤波增益方程：

2 多传感器平台数据融合

由上述分析可知，卡尔曼滤波采用的是一个最佳回归数据处理准则，具有以下两个特点。1）优化：利用所有的测量数据去求出最佳的状态估测。2）回归：不需保存过去测量数据，只处理当时的测量的最新数据。然而，卡尔曼滤波主要是以线性状态模块和测量模块为基础，但实际中许多的物理系统常常是用非线性系统方程式来描述，所以必须将修正卡尔曼滤波来作非线性系统方程式。在这种情况下，可以采用多传感器信息融合(Multisensor Information Fusion)来克服。

多传感器信息融合技术首先是从军事领域发展起来的技术，主要优点是在于观测信息的重复性和互补性上可提供更好的性能，而且在工程上也广泛地应用在机器人学（robotics）、监视系统（surveillance）和自动化制造技术（manufacturing automation）上。一般来说，多传感器信息融合技术在测试应用上会分为两种不同的情况：同种类型传感器信息融合和不同种类型传感器融合。在本文的研究中采用的同类型的传感器信息融合。

在本系统中，采用等间隔分布的5个声纳来测定机器人周围障碍物的距离和合作机器人的距离。超声波测距的原理是利用控制电路发出一个脉波驱动超声波，使发射器发射一小段时间的超声波信号，直到信号遇到障碍物反射回来后，通过接收器将反射回来的超声波接收。因此只要计算发射到接收超声波讯号的时间，即可算出超声波模块与障碍物的距离。用户可以根据多传感器的数据建立机器人的导航图谱，进行多传感器融合。

将上述卡尔曼滤波定位技术与多传感器平台相结合，提出两种融合方案：1）状态变量融合。该方法主要是针对个别传感器分别用卡尔曼滤波器的定位估计技术而得到的状态向量值，这些值再经由数据融合技术而得到最佳的状态向量。2）观测向量融合。该方法主要是针对个别传感器直接经由数据融合技术而得到一个权重值，再利用卡尔曼滤波器的估计技术来获得最佳的状态向量估计值。如图1(a)、(b)所示。本文采用的是第二种方案，权值采用相同值0.2。

图1 基于信息融合和卡尔曼滤波的移动机器人定位

3 仿真实验

首先用如图2所示的运动轨迹方程生成一组全局坐标系下真实的移动机器人坐标值。比较卡尔曼滤波器算法和本文所提出的多传感器融合卡尔曼滤波算法，从结果可以看出，多传感器融合卡尔曼滤波算法与真实的轨迹基本一致，得到的定位结果非常准确。

图2 定位估计结果对比

4 结束语

尔曼滤波是移动机器人进行自主定位的首选方法之一，然而，它主要是以线性状态模块和测量模块为基础，但实际中许多的物理系统常常是用非线性系统方程式来描述。为了提高这种情况下的定位精度。为了提高这种情况下的定位精度，本论文提出一种基于多平台下传感器融合的移动机器人精确定位技术。将多个传感器得到的距离参数，借助于卡尔曼滤波来进行定位。既可以采用多个状态变量的融合策略，又可以采用观测变量融合的策略。数值模拟结果显示，相比融合前，该方法能够获得更加精确的定位。

[1]R.Simmons, S.Koening, Probabilistic navigation in partially observable environments[C], in: Proceedings of the International Joint Conference on Artifi cial Intelligence,Montreal, Que., Vol.2, 1995, pp.1660-1667.

[2]Mohinder S.Grewal, Angus P.Andrews, Kalman Filtering:Theory and Application[M], John Wiley& Sons, Inc.Canada 2001.

[3]R.G.Brown and P.Y.C Hwang, Introduction to Random Signals and Applied Kalman Filter[M], Second Edition,Wiley, New york, 1992.

[4]Grewal, Mohinder S., Andrews, Angus P., Kalman Filtering: Theory and Practice Using MATLAB Second Edition[M], John Wiley&Sns Inc., January 2001.