基于改进ReliefF算法的特征加权FCM
张 鸿
(船舶重工集团公司723所,扬州225001)
0 引 言
聚类分析是多元统计分析的方法之一,是统计模式识别中非监督模式分类的一个重要分支[1]。分类模式识别常采用基于欧式距离的最近邻分类器来实现。在一般欧式距离中,样本在个体特征上的差异对总距离的贡献是相同的,对样本分类所起的作用也是相同的。但是对象间的距离表示对象的相近程度,而相似不仅依赖于对象间的相似程度,还依赖于对象内的性质,即对象中每个变量的重要性是不同的,对样本分类所起的作用也有所不同。原则上,对每个模式知道的信息越多,聚类的效果应该越好。然而在实践中并非如此。有些特征可能是噪音数据,这些噪音数据对聚类结果没有贡献甚至可能降低聚类效果。
模糊C均值聚类(FCM)分析就是一种有效的聚类分析方法,在非监督模式识别、模糊控制等领域有着极为广泛的应用[2]。原始的FCM假定待分析样本的各维特征对分类的贡献均匀,不考虑各个特征对分类的不同作用。
利用特征权值对分类器的距离计算进行加权,对样本分类越有利的特征权值越大,样本在该特征维上即使出现微小的差异也会因较大的加权对欧式距离的计算产生较大的影响。因此,采用特征加权的欧式距离进行最近邻分类可以取得更好的分类效果[3]。所以本文比较了基于不同的特征权值计算方法的加权FCM的聚类效果,并最终提出了一种改进的ReliefF算法加权FCM聚类算法。
1 特征权重计算方法
1.1 基于信息增益的特征权重计算方法
信息增益(IG)特征权重计算方法是最简单的特征评价方法[3]。
令W为样本实例的第n个特征,M为该样本实例的类变量。在观察到W前后,类变量M的墒为:

式中:a=1,2,…,n;c=1,2,…,C,C 为数据集所分成的类别。
在观察到W 后,类变量M的墒的减少量反映了特征W 所承载的关于W 的信息量,即为信息增益[3]:

1.2 原始ReliefF算法
对于任意一个样本实例xi,基本的ReliefF算法可以表示为:
首先找出k个与xi同类的最近邻的样本实例集合H。设diff_hit(A,x,H)是n×1矩阵,表示对象xi与H内各对象在样本属性特征A上的差异量化表示:

式中:j=1,2,3,…,k。
其次找出与xi不同类的样本实例中k个最近邻的样本集合 M(c)。设 diff_miss[A,xi,M(c)]是n×1矩阵,为xi在与M(c)内各对象在样本属性特征A上的差异量化表示:

设输入:训练样本集X,最近邻样本个数k,重复累积次数m;输出:样本特征权重值矩阵W。由上述描述可以得到基本的ReliefF算法基本步骤如下:
(1)设置所有的属性权重值;(2)for i:=1to m;
(3)随机选择一个样本实例;
(4)找到与样本同类的k个最近邻样本集合H;
(5)for each class c≠class(xi);
(6)找到与样本xi不同类的k个最近邻样本集合M(c);
(7)for A:=1to n;
(8)W[A]:= W[A]-diff_hit(A,xi,H)/(k·m)+diff_miss[A,xi,M(c)]/(k·m);
(9)end。
在上述伪代码中,H表示与对象同类的k个最近邻的对象集合,M(c)表示与对象不同类的k个最近邻对象集合,diff_hit(A,xi,H)为对象xi与H内各对象在特征A 上的差异量化表示,diff_miss(A,xi,M)表示对象xi与M(c)内各对象在特征A上的差异量化表示,上述两公式的计算方式见公式(4)、(5)。
1.3 改进的ReliefF算法
要对样本属性权重值做出最有效的评估,必须使选取的累积样本尽量均匀地覆盖于每个样本类别的整个样本数据集中。如果ReliefF算法不能确保选取的样本均匀地覆盖于每个样本类别的整个样本数据集中,必然会造成下列的一些问题:
首先基本ReliefF算法重复了m次从训练样本集中随机挑选样本xi的操作,m一般要远小于样本总数量。如果原始数据集的样本集中在某几个类别中,按照基本的ReliefF算法随机选择样本数,必然会造成以下的缺点:属性权重值向样本数量多的类别倾斜。包含样本数较多的类别其样本点被随机选中的概率较大,与该类别相关的属性权重值累积就会较高。反之,一些样本数较少的类别由于其样本点被选中的几率小,即使有对分类起明显作用的属性权重值也会因为累积少而被掩盖[2]。
其次由于F次迭代使用的样本都是随机选择的,即使是同一组训练样本集,每运行一次该算法,算法随机选中的样本点都不可能完全相同,这样造成的累积的属性权重值也有波动。
由于基本的ReliefF算法存在上述缺点,通过上述算法计算出来的属性特征权值必然存在一定的偏差,所以本文提出了改进的ReliefF算法(IReliefF)。由于基本ReliefF算法的不足之处主要体现在样本点的选择上,本文采取下列措施来对样本点选择方法进行改进:为保证每类样本均可参与权值计算,在选择样本时,从每类目标样本分别各抽取m个样本点用于属性特征权重值的累积。改进的样本点选择步骤如下:
(1)计算每一类样本的样本中心点Xd;
(2)计算该类中样本点与该样本中心点的欧式距离;
(3)根据Xd大小,把该类样本分成f组,每组间隔欧式距离大小为 Δd,Δd= [max(Xd)-min(Xd)]/f ;
(4)在分出的F组的每一组,取中间的样本做ReliefF分析。
结合基本的ReliefF算法和上述样本点选择办法,得到了IReliefF算法的基本步骤如下:
(1)设置所有的属性权重值;
(2)for each class,ci,i=1,2,…,T;
(3)计算该类中样本点与该样本中心点的欧式距离dij;
(4)根据dij大小,计算每组间隔欧式距离Δd;
(5)选择距离组内的中间样本xj;
(6)for each xj,j=1,2,3,…,f;
(7)找到与样本xi同类的k个最近邻样本集合H;
(8)for each class c≠class(xi)do;
(9)找到与样本xi不同类的k个最近邻样本集合 M(c);
(10)for A:= 1to n do,W[A]:=W[A]-diff_hit(A,xi,H)/(f·k·T)+diff_miss[A,xi,M(c)]/(f·k·T);
(11)end。
IReliefF算法可以计算样本属性权重值矩阵W。权重值的取值范围在[-1,1]区间,值越高的特征对分类越有利,值为负的特征则不利于分类,并且可以得到稳定的W。
2 加权的模糊C均值聚类算法
原则上,对每个模式知道的信息越多,聚类的效果应该越好。然而在实践中并非如此。有些特征可能是噪音数据,这些噪音数据对聚类结果没有贡献甚至可能降低聚类效果。参考文献[3]提到学习属性权值可以普遍提高聚类质量,学习属性权值使无关属性的影响尽量减小,甚至权值可以为零。所以本文提出用基于IG和改进的ReliefF算法来计算数据特征的权重值,提出加权的FCM(WFCM)来提高聚类质量,尽量减少噪音数据的影响。
在Dunn提出的C-MEANS距离算法的基础上,Bezedk加以推广[7],提出了模糊 C-均值聚类算法。FCM是一个典型的基于距离的聚类算法。该算法具有简单、高效的特点,并能收敛于局部最优解。
FCM的目标是使价值函数J值达到最小,价值函数J的定义为:

式中:m∈[1,+∞],为一个加权指数,随着m的增大,聚类的模糊性增大;N为样本数据集的个数;μij为第j个样本点隶属于第i类的概率值。
加权的欧式距离为:

加权的FCM(WFCM)算法的目标函数为:
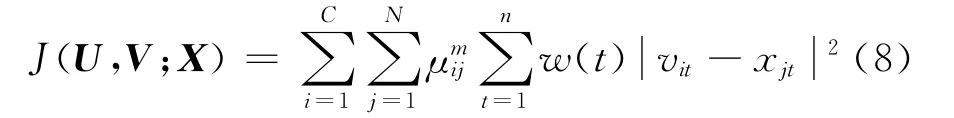
式中:w(t)为各个属性的权重值。
WFCM算法实现基本步骤如下:
(1)设置隶属度矩阵U 到[0,1];
(2)for i:=1to c do;
(3)找到聚类中心vi;
(4)end;
(5)for j:=1to maxiter;
(6)计算目标函数值J;
(7)如果2次循环的目标函数值差值小于设定值;
(8)break;
(9)更新隶属度矩阵U;
(10)end。
3 实验与分析
3.1 实验数据
实际试验数据选用UCI机器学习数据库,该数据库是由加州大学提供,从中选择Iris、Disbetes等2个数据集,如表1所示。

表1 实验数据集
3.2 实验分析
本实验从分类正确率和分类标准差指标方面,在本实验数据集上对 ReliefF-WFCM、IReliefFWFCM、IG-WFCM以及原始FCM等4种聚类方法的性能进行比较。
ReliefF-WFCM表示使用原始的ReliefF算法进行加权的FCM,IReliefF-WFCM表示使用改进的ReliefF算法进行加权的FCM,IG-WFCM表示利用信息增益算法进行进行加权的FCM,FCM表示使用原始的模糊C均值聚类。
对于基本的ReliefF算法,本实验选择从训练样本集合中随机抽取的用于特征累积的样本数量m占到样本数据集总样本数的20%,样本最近邻数k=10,基本的ReliefF算法每次的结果不同,本实验选取10次结果的平均值作为最终的平均值。对于IReliefF算法,每类抽取的样本点数为m/c,从而保证2种算法的抽取样本点数一致。样本最近邻数k=10,m为基本ReliefF算法抽取的样本点数,c为样本数据集的类别数。
为了使实验结果更加可靠,本实验采取5折交叉验证的方式。n折交叉验证原理:n就是要拆成几组。对于k个子集,每个子集均做一次测试集,其余的作为训练集。交叉验证重复k次,每次选择一个子集作为测试集,并将k次的平均交叉验证正确率作为结果。
由表2、表3可得,IG-WFCM、ReliefF-WFCM和IReliefF-WFCM最终得到的误分率指标和标准差指标都要优于原始的FCM聚类算法,从而可验证学习属性权值确实可以普遍提高聚类质量。

表2 数据集Iris聚类结果分析

表3 数据集Disbetes聚类结果分析
通过对IG-WFCM、ReliefF-WFCM、IReliefFWFCM聚类结果的比较可以看出:在误分率指标方面,ReliefF-WFCM、IReliefF-WFCM 聚类效果要比IG-WFCM的聚类效果好;但是在标准差指标方面,IG-WFCM的聚类效果要优于ReliefF-WFCM,仍然劣于IReliefF-WFCM的聚类效果。从而验证了基本ReliefF算法的缺点:得到的属性权重值不稳定,从而造成加权FCM结果不稳定。
聚类结果无论是在误分率指标还是在标准差指标上,IReliefF-WFCM算法的误分率和标准差都比较小,数值变化幅度也比较小,从而说明该算法的性能比较稳定。IReliefF-WFCM验证了较高的聚类精度。基于改进ReliefF算法的加权FCM的聚类效果要优于基于基本ReliefF算法的加权FCM。
4 结束语
本文提出了一种基于改进的ReliefF算法的加权FCM(IReliefF-WFCM)聚类方法,对基本 ReliefF算法样本选择方法实现了改进。实验结果表明,该算法减少了基本FCM聚类结果的误分率和标准差,提高了FCM聚类结果的精度和稳定性,为以后该算法用于实际数据处理打下了坚实基础。
[1]何清.模糊聚类分析理论与应用研究进展[J].模糊系统与数学,1998,12(2):89-94.
[2]李洁,高新波,焦李成.基于特征加权的模糊聚类新算法[J].电子学报,2006,34(1):89-92.
[3]高滢,刘大有,徐益.一种特征加权的聚类算法框架[J].计算机科学,2008,35(10):152-154.
[4]Liu Chengjun.Gabor-based kernel PCA with fractional power polynomial models for face regcognition[J].IEEE Transaction on Pattern Analysis and Machine Intelligence,2004(5):572-581.
[5]Kononenko I.Estimating attributes:analysis and extensions of ReliefF[A].The Proceedings of The European Conference on Machine Learning on Machine Learning[C].Italy,Catania:Springer-Verlag New York,Inc.,1994:171-182.
[6]Kira K,Rendell L A.A practical approach to feature selection[A].The Proceedings of The Ninth International Workshop on Machine Learning[C].United Kingdom,Aberdeen,Scotland:Morgan Kaufmann Publishers Inc.,1992:249-256.
[7]Bezdek J C,Ehrlich R,Full W.FCM:the fuzzy c-means clustering algorithms[J].Computers & Geosciences,1984,10(2):191-203.

