升阻互补型垂直轴风轮的结构动态分析

顾圣东 ，葛海明 ，王小龙

(1.河海大学港口海岸与近海工程学院，江苏 南京 210098;2.中国人民解放军92301部队，北京 100841;3.江苏省电力设计院，江苏 南京 211102)

垂直轴风力发电机的发展虽然比水平轴风力发电机晚，但是随着科学技术水平和人类认识水平的提高，关于垂直轴风力发电机的研究越来越多，垂直轴风力发电机将最终满足家用中小型风力发电的发展趋势[1-2].升阻互补型垂直轴风力发电机的研制思路就是把升力型和阻力型2种垂直轴风力发电机互相耦合并充分发挥各自的性能优点，使功率系数最大化.具有设计简单、容易起动、运行安静、抗风能力强、发电功率上升平缓、安装与维修的周期与成本低，以及在最大限度利用风能资源的同时，获得更大的发电量等优势[3].

风力发电机的风轮长期承受旋转产生的周期性荷载以及风力荷载[2]，因此作为风力发电机组中最重要的组成部分之一，风轮结构设计是否合理，直接影响着机组的性能[4]，关系到风能的转化效率、叶片的使用寿命、材料使用的经济性，以及制造工艺的可行性等[2].

本文以10kW升阻互补型垂直轴风力发电机的风轮为例，计算并分析了叶片支撑和升力型叶片的结构特性.

1 风轮结构与材料

本文分析的10kW升阻互补型垂直轴风力发电机的设计风速为10m/s;叶片尖速比为0.55;叶片密实度取0.2.风轮由三叶片H型风轮与三叶片直筒式阻力型风轮组成，升力型叶片翼型为NACA0018，旋转半径为3m，高8m;阻力型叶片为直筒式翼型，高4m，旋转半径是升力型叶片的1/5，如图1所示.

升力型叶片和阻力型叶片通过横梁、横梁基座、阻力叶片座、法兰组装于风力发电机的风轮上.横梁需要能够承受叶片自身的重力和受力以及运行时产生的交变荷载，因此其强度设计和动力性设计尤为重要.上、下横梁均在一根长为2840mm的无缝钢管上加工，上横梁的外径为102mm，壁厚10mm，下横梁的外径为152mm，壁厚10mm.钢管借助于一个特制的法兰，与横梁基座相连接.上、下横梁基座同样在2根无缝钢管上加工，并且绕钢管焊接了3个法兰盘，与横梁连接.

阻力型叶片通过Z形阻力叶片座与U形板固定在横梁上.升力型叶片采用空腹加筋结构，用玻璃钢作肋骨架和蒙皮.蒙皮具有翼型的曲面和叶片的扭转形状.铆钉和环氧树脂黏结剂将蒙皮、肋骨架装配黏结在一起.蒙皮和肋骨架均厚6mm，叶片内部用泡沫材料填充.

叶片支撑用材为45号型钢，计算时的杨氏模量按210GPa计，泊松比约为0.3，密度约为7850kg/m3，许用强度取237MPa，许用抗拉强度不小于300MPa[5].玻璃钢中玻璃纤维含量(设定)为55%.机械力学性能为:拉伸强度220MPa，拉伸模量12GPa，弯曲强度240MPa，弯曲模量12TPa，压缩强度160GPa，冲击强度65kJ/m2，巴克尔硬度40，表面平整光滑.

图1 风轮结构组装Fig.1 Structure of wind wheel

2 结构动态计算

2.1 模态计算

对于仅受重力作用时风轮的动态特性问题，需要分析其振动模态，从而确定风力发电机在额定转速下的各阶固有频率及振型.在模态计算中，假设风力发电机塔架的变形均为小变形且所使用材料为弹性体，由此有结构振动系统的运动方程为

式中:M——塔架质量矩阵;C——塔架阻尼矩阵;K ——塔架刚度矩阵;F——塔架外载荷列阵;¨q，q——节点的加速度、速度和位移的列阵.

结构系统在无阻尼情况下自由振动，即C=0且F=0时，则有结构振动的运动方程:

设方程的初始条件为

则式(2)的通解为

将式(3)代入初始条件可得

将式(4)代入式(2)，有系统无阻尼状态下的角频率特征方程为

因此，结构系统第j阶振动频率为

结构系统为受迫振动，即F≠0.则系统的运动方程为

式(7)的解可以分为通解(8)与特解(9):

将式(9)代入式(7)可得

所以，结构系统受迫振动方程为

可见，当 ωij趋向ω时，结构系统的振幅将趋向于无穷，这就是共振现象[6-7].固有频率取决于系统本身的物理参数，自由度为n的无阻尼自由振动是由n个以固有频率作简谐振动的系统线性组合[8].

2.2 简谐响应分析

简谐响应分析是确定结构在已知频率的简谐荷载作用下结构响应的技术，其输入通常为已知大小和频率的简谐波荷载，或者同一频率的多种荷载.输出为每一个自由度上的简谐位移、应力与应变等.

风轮对塔架的激励就是一个周期性变化的动荷载，可简化为和转速具有相同周期的简谐载荷:

式中:Fa——平均载荷;Fp——脉动载荷幅值;b——叶片数;ω——角频率.结构响应位移为

式中:Aij——第 j阶振型第i点的振幅比;mi——第i点的集中质量.

简谐响应分析用于确定线性结构在承受(简谐)规律变化载荷时的稳态响应.分析的目的是计算出结构在几种频率下的响应并得到响应值对频率的曲线.从这些曲线上可以找到峰值响应，并进一步观察峰值频率对应的应力.简谐响应分析使设计人员能预测结构的持续动力特性，从而使设计人员能够验证其设计能否成功地克服共振、疲劳，及其他受迫振动引起损害的效果[8].

3 计算结果及分析

3.1 风轮结构动态计算分析

由于风轮是质量和弹性均匀分布的连续体，所以自由度为无穷，可以提取的特征模态也比较多.在实际情况下，外界激振力的频率一般都不高，只有前几阶结构固有频率与激振力的频率相接近，值得重点关注[9].笔者提取了风轮的前6阶低阶振型、频率以及垂直轴风力发电机塔柱的谐响应曲线，阶次用MODE-i(i=1，2，3 ，4，5，6)表示，进行分析比较，见表 1和图 2、图 3.

从计算结果可以得出:风轮的前6阶模态分为2个阶段，前3阶模态为第1个阶段，模态表现为升力型叶片的弯曲变形，后3阶模态为第2个阶段，表现为6根阻力型叶片加强筋的弯曲变形.根据公式f=可知，在系统正常工作时，即以160r/min的转速运行，风轮旋转产生的频率为2.6667Hz，接近风轮的第一阶固有频率，容易导致结构的自振.风轮从0r/min加速到160r/min需要跨过风轮的前2阶固有频率.自然风通常是不稳定的，当其速度比较小，风轮转速不能达到额定转速时，风轮旋转频率容易游走于风轮第1，2阶固有频率之间，造成升力型叶片使用寿命的缩短.

表1 垂直轴风力发电机前6阶固有频率Table 1 First six-order natural frequencies of vertical axis wind turbine

图3表示风轮在以额定转速运行时的响应曲线.由图3可以看出风力发电机在2.7Hz附近会产生共振.由此可见，当风轮以设计额定转速160r/min运行时，其产生的简谐荷载将对风力发电机具有十分严重的破坏性.而风轮的前3阶模态主要表现为升力型叶片的变形，因此还应该重点计算升力型叶片.

3.2 升力型叶片受力分析

研究升力型叶片的流体诱导振动，主要是研究不稳定流动条件下叶片表现出来的振动特性，并建立流动特征与振动特性之间的联系.

为了封闭流场求解的方程，引入基于 Shear Stress Transparent(SST)近壁区方程的k-ω湍流模型，该模型能够精确地预测近壁区的流动现象[10].

图2 风轮的前6阶模态Fig.2 First six-order modal characteristics of wind wheel

升力型叶片受到重力、离心力和风载作用.风载为运动来风和自然来风的合成，如图4所示.计算时，自然来风取额定风速10m/s和设计最大风速45m/s，荷载采用分角度计算.

在运行时，叶片主要受到拉应力的作用，蒙皮上的纤维采用对称铺设，其中±45°纤维各2层，0°纤维 8层，厚6mm.对铺设好的叶片施加荷载，并借助Tsai-Hill失效准则对叶片进行分析，分析得叶片上最大失效值为0.0207，远小于1，因此叶片在荷载作用下是安全的.

图3 钢塔柱频率响应曲线Fig.3 Frequency response curve of steel tower pillar

3.3 结果分析

从风轮结构模态的计算可以看出，风轮结构的安全性存在巨大的隐患.经计算，在荷载作用下，叶片支撑的最大等效应力值为156.54MPa，第一主应力最大值为277.24MPa，接近45号型钢的许用强度，并都位于支撑的钢管横梁上.

提高风轮的固有频率可以有效降低结构自振现象产生的几率.固有频率通常取决于结构自身的质量和刚度，自身质量越轻，用材的刚度越大，结构的固有频率就越高.根据风轮结构的静态计算结果，其不适合单纯通过改变钢管横梁规格的方式达到叶片支撑优化的目的，因此建议更换横梁的材料.本文以碳纤维为例，将叶片支撑的横梁换成大口径碳纤维管，材料纵向杨氏模量为180.4GPa，横向杨氏模量为10.3GPa，泊松比0.3，密度1600kg/m3，纵向许用抗拉应力1700MPa.在约束不变的情况下，提取风轮的前6阶频率，结果如表2所示.

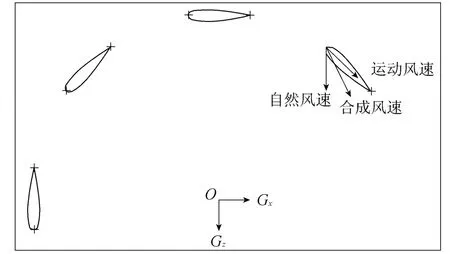
图4 叶片计算攻角示意图Fig.4 Sketch map of attack angle of blade

因此风轮从0r/min加速到160r/min时，不再需要跨过结构的前2阶固有频率;也不再需要考虑风轮转速较低时，其旋转频率游走于第1，2阶固有频率之间而造成的结构疲劳损坏，提高了整体结构的安全性.

表2 优化后的风轮前6阶固有频率Table 2 First six-order natural frequencies of wind wheel after optimization

4 结 语

本文基于有限元计算，对10 kW升阻互补型垂直轴风轮的结构动态进行计算，得到了升力型叶片的受力情况.分析了结构固有频率对额定转速的影响，揭示了固有频率随结构变化的规律，为风力发电机风轮的结构优化提供了依据.

[1]贺德馨.风工程与工业空气动力学[M].北京:国防工业出版社，2006:56-57.

[2]李俊峰，王景丽，施鹏飞.风力在中国[M].北京:化学工业出版社，2005:68-70.

[3]蒋超奇，严强.水平轴与垂直轴风力发电机的比较分析[J].上海电力，2007(2):163-165.(JIANG Chao-qi，YAN Qiang.Comparative Study on the horizontal axis and vertical axis wind turbine[J].Shanghai Electric Power，2007(2):163-165.(in Chinese))

[4]JACOB A.Another record year for wind energy[J].Reinforced Plastics，2006(4):26-27.

[5]AETAL M.Structural damagedetection by asensitivity and statistical-based method[J].Journal of Sound and Vibration ，2004 ，216(5):791-818.

[6]MOAVENI S.Finite element analysis theory and application with ANSYS)[M].2nd edition.北京:电子工业出版社，2005:406-460.

[7]张宪，何洋，钟江，等.疲劳振动试验台的模态与谐响应分析[J].机械设计与制造，2008，4(4):12-14.(ZHANG Xian，HE Yang，ZHONG Jiang，et al.Modal and harmonic analysis of fatigue vibration test-bed[J].Machinery Design&Manufacture，2008，4(4):12-14.

[8]孙彦锋.基于ANSYS的龙门起重机结构系统谐响应分析[J].现代机械，2009，32(3):32-33.(SUN Yan-feng.The structural system of gantry based on ansys responds analyzing humorously[J].Modern Machinery，2009 ，32(3):32-33.(in Chinese))

[9]马昊星.水平轴风力发电机桨叶的计算模态分析[J].太阳能学报，2002，23(3):361-365.(MA Hao-xin.Rotor blade modelling for the hawt[J].Journal of Solar Energy Machinery，2002，23(3):361-365.(in Chinese))

[10]付磊，黄彦华，朱培模.水轮机转轮叶片流固耦合水力振动分析[J].水利水电科技进展，2010，30(1):24-26.(FU Lei，HUANG Yan-hua，ZHU Pei-mo.Fluid-structure coupling hydraulic vibration of hydraulic turbines[J].Advances in Water Science and Technology，2010，30(1):24-26.(in Chinese))

[11]徐小韵，郑源，赵振宙，等.基于计算流体动力学的S型风力发电机性能分析[J].河海大学学报:自然科学版，2010，38(3):332-336.((XU Xiao-yun，ZHENGYuan，ZHAOZhen-zhou，et al.Evaluation of performance of Savonius rotors based on computational fluid dynamics[J].Journal of Hohai University:Natural Sciences，2010，38(3):332-336.(in Chinese))

[12]马宏忠，徐树峰，鞠平，等.基于直流发电机的风力发电系统及其控制策略[J].河海大学学报:自然科学版，2007，35(3):334-337.(MA Hong-zhong，XU Shu-feng，JU Ping，et al.Research on wind power generation system based on DC generator and its control strategy[J].Journal of Hohai University:Natural Sciences，2007，35(3):334-337.(in Chinese))