若干非线性偏微分方程的守恒律
白玉梅
(内蒙古民族大学 数学学院,内蒙古 通辽 028043)
0 引言
构造微分系统的守恒律是数学物理研究的重要课题.守恒律反映物理量不随时间而改变的现象,在研究微分系统,尤其是可积系统和孤立子理论中发挥重要作用[1].如利用守恒律获得微分系统的精确解、分析解的各种特性和构造Hamilton系统等.一般情况下,如果一个微分系统有孤立子解,则其存在无穷多个守恒律,拥有无穷多个守恒律的非线性微分系统可积;然而,没有无穷多个守恒律的微分系统仍可能可积,如Burgers方程.除此之外,守恒律被广泛应用于一些数值方法的发展上,如有限元法和非连续Galerkin方法.由此可见,寻找物理背景明确的非线性系统的守恒律十分必要.
以(1+1)维非线性弹性波动方程、Brusselator方程组和(2+1)维广义CBS方程作为研究对象,以符号计算软件Maple为工具,采用第一同伦公式法,分别构造这3个方程(组)的守恒律.
1 守恒律构造方法
构造微分系统守恒律的方法包括直接法[4]、标量公式法、第一同伦公式法[2-3]、第二同伦公式法、利用对称和共轭方程(组)法[5-7]、Lax对方法、迹恒等式法和Bäcklund变换法[8]等,文中采用第一同伦公式法.
设自变量x=(x1,x2,…,xn),因变量u=(u1,u2,…,um).
步骤1 计算系统相应的n维欧拉算子

步骤2 计算n维拓扑算子
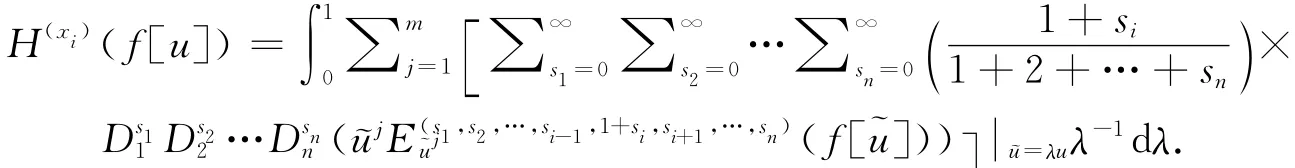
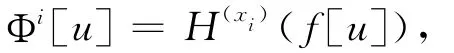
步骤3 由步骤2所得结果,得到通量进而通过全导数算子作用,得到形如的微分系统的守恒律.
2 构造非线性偏微分方程的守恒律
2.1 弹性波动方程
非线性弹性波动方程为

式中:γ为任意常数.文献[9]应用Lie对称法,在不同对称的恒等条件下,变换方程(1)为常微分方程,进而获得若干不变解.
首先,假设其特征
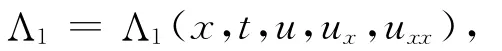
得到关于特征Λ1的化简后的确定方程组,即
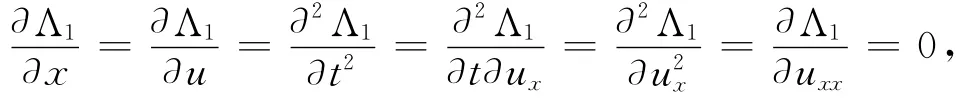
经计算,有特征
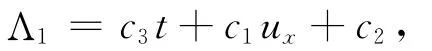
式中:c1,c2,c3为参数.
选取参数并利用第一同伦公式计算通量,得出3种情形:
情形1 c1=1,c2=c3=0,特征Λ1=ux,通量
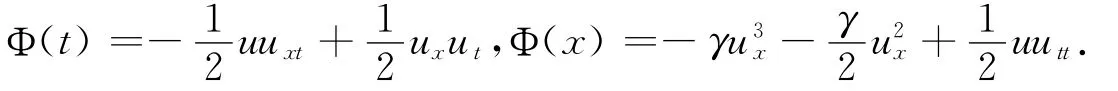
情形2 c2=1,c1=c3=0,特征Λ1=1,通量
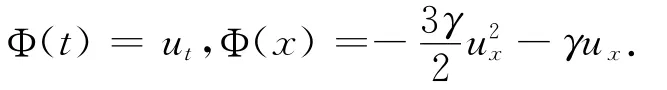
情形3 c3=1,c1=c2=0,特征Λ1=t,通量
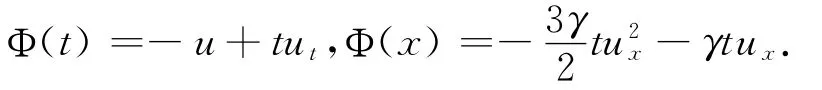
可得方程(1)的守恒律,即
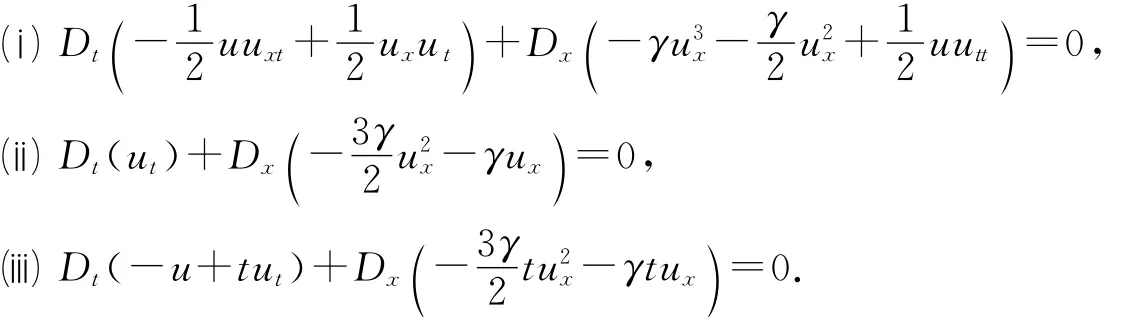
2.2 Brusselator方程组
Brusselator方程组为
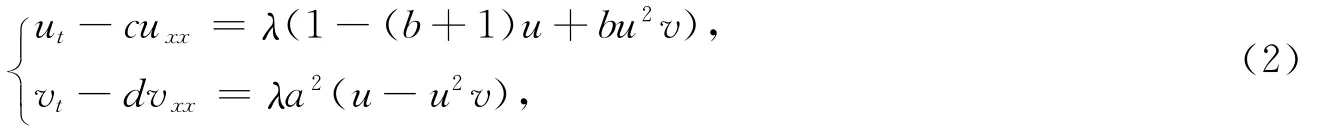
式中:c,d为扩散系数;a,b为其他反应物的固定浓度;λ为衡量容器大小的参数.首先计算方程组(2)的特征,设a,b,c,d,λ均不为0,且c-d≠0,令
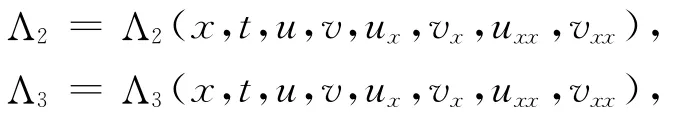
求解化简的确定方程组,得
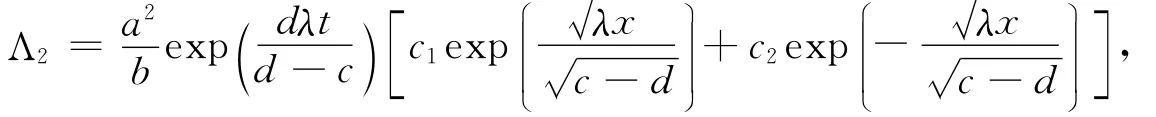
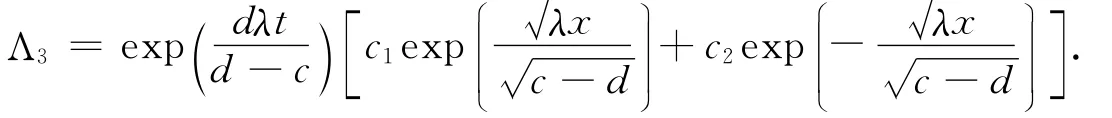
选取参数,并利用第一同伦公式计算通量,得出2种情形:
情形1 当c1=1,c2=0时,特征
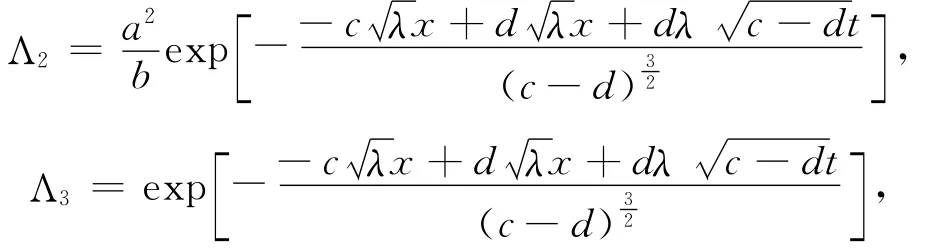
通量
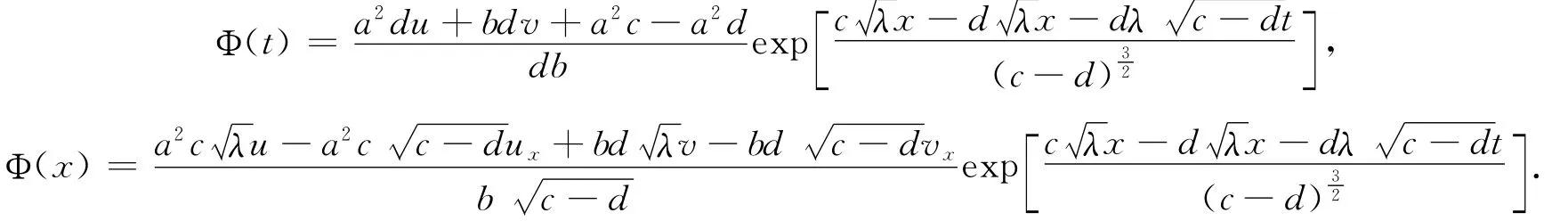
情形2 当c2=1,c1=0时,特征
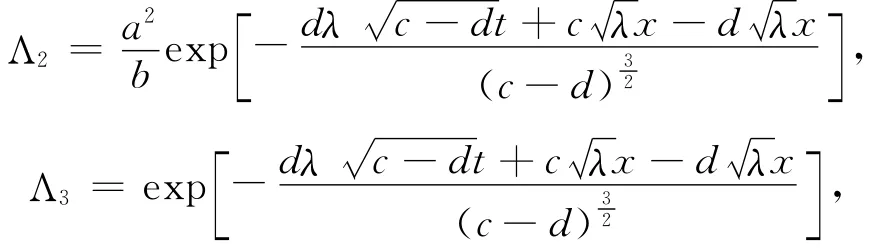
通量
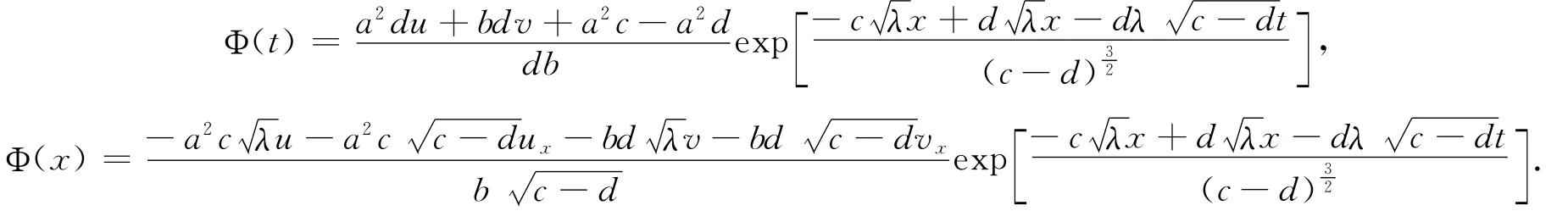
可得方程组(2)的守恒律,即
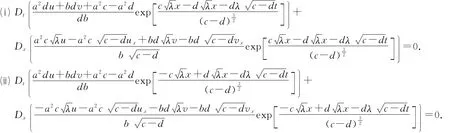
2.3 广义CBS方程
广义CBS方程为
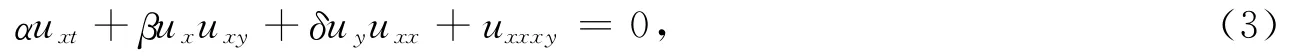
式中:α,β,δ为任意常数,α≠1,β≠0,δ≠0.
Zhang Huan Ping等通过Painlevé检验,得到方程(3)可积的条件,给出无穷多对称并对其进行对称约化[10].设特征
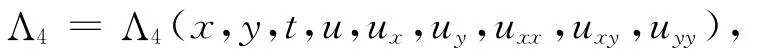
计算关于Λ4的确定方程组
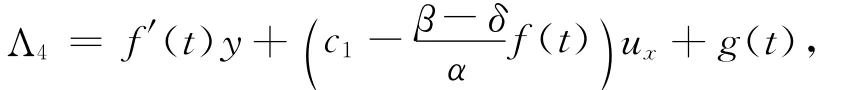
式中:α,β,δ,c1为任意常数,α≠0,δ≠β;f(t),g(t)为可微的任意函数.
选取参数并利用第一同伦公式计算通量,得出3种情形:
情形1 设c1=1,f(t)=0,g(t)=0时,特征 Λ4=ux通量

情形2 设c1=0,f(t)为任意函数,g(t)=0时,特征
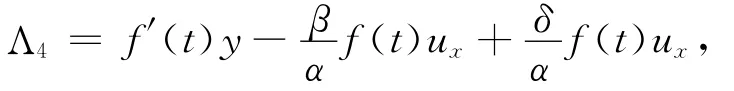
通量
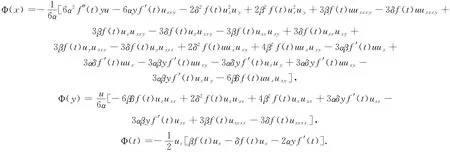
情形3 设c1=0,f(t)=0,g(t)为任意函数时,特征 Λ4=g(t)通量
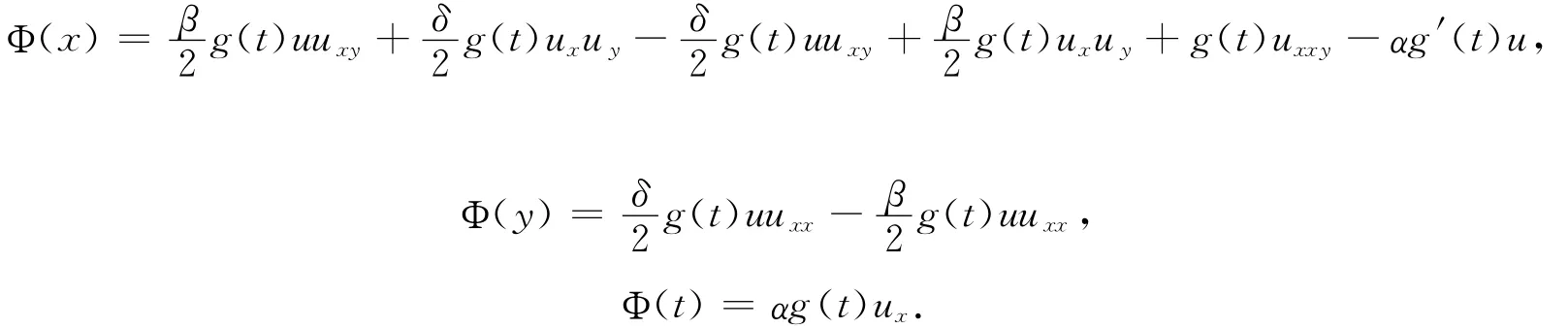
可得方程(3)的守恒律,即
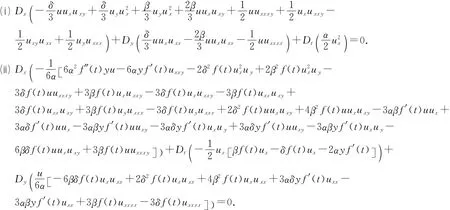
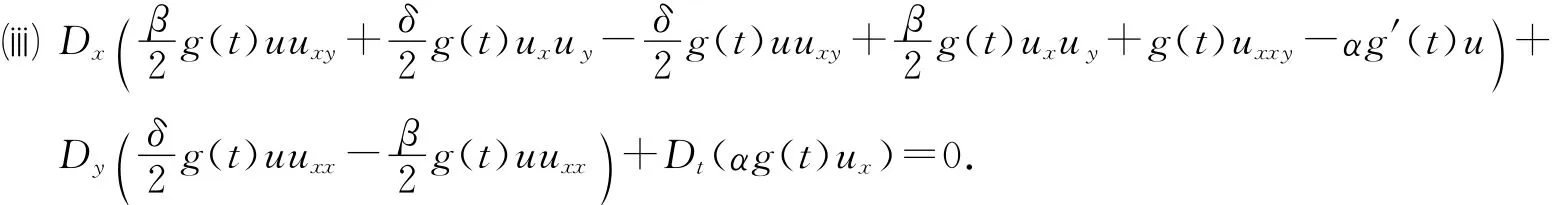
3 结束语
将第一同伦公式法应用到物理背景明确的(1+1)维非线性弹性波动方程、Brusselator方程组和(2+1)维广义CBS方程守恒律的构造中,在求得结果的同时,进一步说明该方法的有效性.该方法还可以用于获得其他非线性偏微分方程的守恒律.
[1]Olver P J.Applications of Lie groups to differential equations[M].New York:Springer-Verlag,1993.
[2]Cheviakov A F.Computation of fluxes of conservation laws[J].Journal of Engineering Mathematics,2010,66:153-173.
[3]Wolf T.A comparison of four approaches to the calculation of conservation laws[J].Europ.J.Appl.Math,2002,13(2):129-152.
[4]Mei Jian qin,Zhang Jing jing,Zhang Hong qing.Direct algorithms for constructing high-order conservation laws of nonlinear partial differential equations[J].Journal of Dalian University of Technology,2011,51(2):304-308.
[5]许斌,刘希强,刘玉堂.耦合 KdV方程组的对称,精确解和守恒律[J].应用数学学报,2010,33(1):118-123.
[6]王婷婷,刘希强,于金倩.Caudrey-Dodd-Gibbon-Kotera-Sawada方程的对称、精确解和守恒律[J].量子电子学报,2011,28(4):385-390.
[7]许斌,刘希强.Landau-Lifshitz方程的群不变解和守恒律[J].量子电子学报,2011,40(5):575-579.
[8]张大军,宁同科.可积系统的守恒律[J].上海大学学报:自然科学版,2006,12(1):19-30.
[9]Tahir Mustafa M,Khalid Masood.Symmetry solutions of a nonlinear elastic wave equation with third-order anharmonic corrections[J].Applied Mathematics and Mechanics:English Edition,2009,30(8):1017-1026.
[10]Zhang Huanping,Chen Yong,Li Biao.Infinitely many symmetries and symmetry reduction of(2+1)-dimensional generalized Calogero-Bogoyavlenskii-Schiff equation[J].Acta Phys.Sin.,2009,58(11):7393-7396.

