某型飞机仪表板振动分析

李善勋

（洪都航空工业集团，江西 南昌 330024）

0 引言

在工程中，经常需要求解结构强迫运动的问题，典型的情况如求桥梁、建筑物在地震时的响应，以及飞机在空中飞行时设备、附件的响应等，这类问题的一个共同特点是人们无法直接获得结构所承受的载荷，而只能得到结构所承受基础施加的加速度、速度或位移随时间和频率的变化信息，利用上述信息，用“大质量法”或拉格朗日乘子法可以解决结构的瞬态或频率响应分析问题。

某型飞机的仪表板是材料为LY12的机加件，飞机的各仪表、显示器都安装在该仪表板上，仪表板通过减震垫及其支持结构安装在飞机的口框梁上。该型飞机在颤振试飞中，仪表板出现了振动情况，据飞行员反映，仪表板的振动频率大约在15 Hz左右，仪表板的振动严重影响了飞行员对飞机的操控，颤振试飞任务也由于仪表板的振动问题而进度减缓。为了解决仪表板的振动问题，分析飞机仪表板随频率变化的加速度响应，本文采用大质量法对飞机仪表板进行了频率响应分析。

1 理论简介

用“大质量法”建立强迫运动模型（图1）。

图1 大质量法模型

在图中，假设M0比m大许多，u··为大质量运动的加速度，“大质量”M0与感兴趣结构之间连接为刚性。假定大质量M0对于感兴趣的结构的激励输入及m的响应均为正弦函数，即输入

为使系统获得加速度u··，需施加的载荷为P=(M0+m)u··，在m远小于M0的情况下，P≈M0u··，用M0代替（M0+m），载荷输入误差为m/（M0+m），这样系统的运动方程为：

式（1）中[M]为质量矩阵，[B]为阻尼矩阵，[K]为刚度矩阵。

假设

其中[φ]为系统的模态变形矩阵，则可把变量从物理坐标系{u(x)}转换为模态坐标系{ξ（ω）}。

把（2）式带入（1）式，两边同除eiwt得

两边同时乘以模态变形矩阵的转置矩阵[φ]T，得

若阻尼矩阵可以被正交，则根据模态正交性（4）式变为：

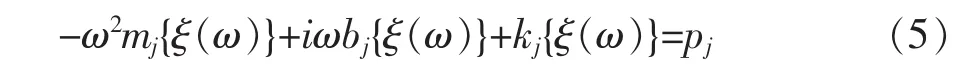
其中，mj＝j阶模态质量，bj＝j阶模态阻尼，kj＝j阶模态刚度，pj＝j阶模态力，（5）式中每阶模态的响应为

再由（2）式可计算出系统在物理坐标下的响应。

2 计算模型建立

2.1 仪表板结构简介

某型飞机原状态仪表板结构三维图如图2所示，仪表板为材料LY12的机加件，厚度为4 mm，边缘厚度为5 mm，仪表板通过上、下4个减震垫与机体结构连接。改进后的仪表板结构如图3所示，仪表板由仪表板主面板和仪表板加强件两部分组成。仪表板主面板为材料LY12的机加件，面板厚度为4 mm，边缘厚度为8 mm，仪表板加强件为材料LY12的机加件，厚度为4 mm至5 mm，仪表板主面板和仪表板加强件用螺栓连接，仪表板加强件通过螺栓与机体结构连接。

图2 某型飞机原状态仪表板三维图

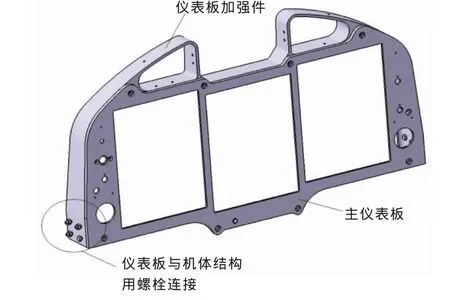
图3 某型飞机仪表板改进方案三维图

2.2 仪表板有限元模型介绍

仪表板有限元模型用体元（Tet10）、点单元、梁元及MPC元建立。仪表板面板、加强件用体元建立，在各显示器及质量较大的仪表重心处创建集中质量点，在集中质量点上施加惯性载荷，通过MPC单元将集中质量点与仪表板骨架相连。原方案与改进方案的仪表板有限元模型如图4、图5所示。

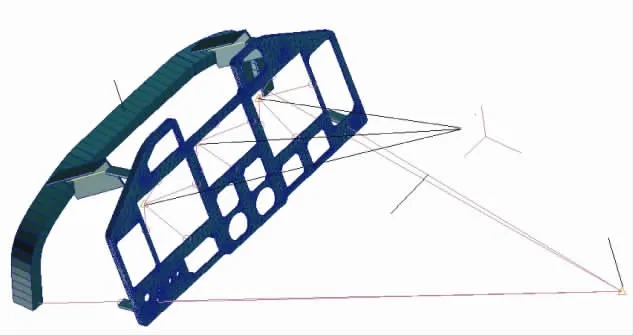
图4 仪表板原方案有限元模型

2.3 大质量的选取及施加

在距飞机仪表板1 000 mm处创建大质量单元，仪表板通过螺栓连接在飞机口框梁上，飞机的质量约为7×103kg，原方案仪表板系统的实际质量为26 kg，根据参考文献，大质量通常取分析模型质量的103～108倍。在实际计算中，一般取分析质量的106倍，所以大质量值取为2.6×107kg，这样处理的结果计算载荷输入误差小于10-6数量级，满足工程要求。大质量在模型中的处理通常有两种方法，一种是在结构的每个约束点上分别施加一个大质量，这种方法会给计算带来误差，另一种方法是把各个约束点用刚性单元连接起来，然后在一个约束点上施加一个大质量。根据以上讨论，计算模型最后确定为把一个2.6×107kg的大质量施加于一用刚性单元连接起来的约束点上，仪表板的有限元模型如图4所示，在大质量上施加一个随频率变化的单位力，根据地面共振试验数据，某型飞机的振动频率范围为0 Hz～80 Hz。用同样的方法选取改进方案的大质量。在计算中采用的载荷曲线如图6所示。

图5 仪表板改进方案有限元模型

图6 载荷随频率变化关系图

2.4 计算方法及参数确定

求解方程（1）可用直接法或模态法，考虑到仪表板有限元模型规模较大，且我们关心的响应频率范围较小（为0 Hz～80 Hz），最后选用模态法。根据模态提取的最高频率至少应大于所关注频率的2倍的原则，在计算中用兰瑟士（Lanczos）法提取了0 Hz～240 Hz范围内的所有模态，飞机仪表板材料为LY12,根据金属材料的特性，选取阻尼系数为0.002。

在以上边界条件下，对原方案和改进方案两种方案进行比较计算（原方案如图2所示，改进方案如图3所示）。

3 计算结果

原方案仪表板的振动加速度随频率变化的曲线如图7所示，从曲线可以看出，在频率为15 Hz左右时，仪表板的振动加速度最大。改进仪表板方案后，仪表板的振动加速度随频率变化曲线如图8所示，从曲线可以看出，在频率为55 Hz左右时，仪表板的振动加速度最大。从计算结果可以看出，两种方案的计算结果差别较大。

图7 原方案仪表板加速度—频率响应曲线

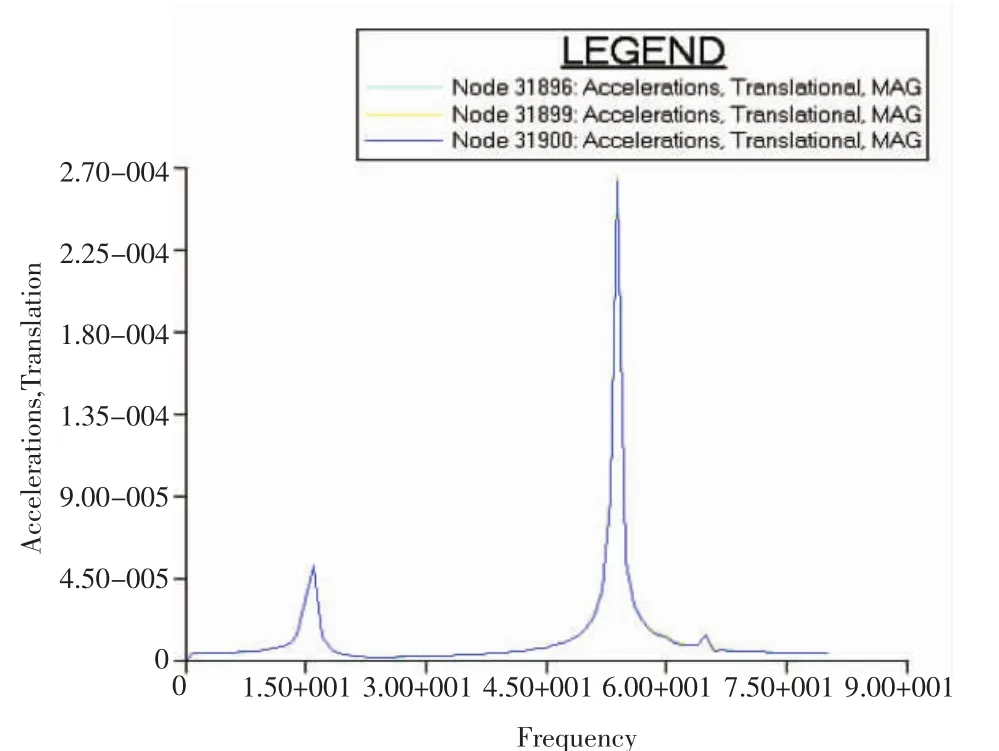
图8 改进方案仪表板加速度—频率响应曲线

4 计算结果分析

从原方案的振动频率响应曲线可以看出，在频率约为15 Hz左右，仪表板的振动加速度最大。由某型飞机的地面共振试验可知，机身垂直一弯、二弯的频率分别为17.59 Hz和29.60 Hz，机身水平一弯的频率为17.77 Hz。仪表板的振动频率很接近机身垂直一弯和水平一弯的频率，由此可以推测，某型飞机在颤振试飞中仪表板发生振动的原因是仪表板的振动频率没有避开飞机机身的振动频率，仪表板的振动是由飞机机体的振动引起的。改进后仪表板的振动频率约为55 Hz左右，避开了飞机机体的振动频率，虽然在15 Hz左右仍有一个峰值，但其对应的振动量级很小，仪表板按改进方案进行改进后，其减振效果很明显。

5 结语

1）原方案仪表板的振动频率与飞机机身的振动频率相接近，同为15 Hz左右。二者频率接近是造成仪表板振动的主要原因；

2）仪表板方案改进后的计算结果显示，仪表板的第一阶峰值频率已转移至55 Hz左右，高于飞机机身的振动频率，与原方案相比，在频率为15 Hz左右时仪表板的振动量级有了明显的减小；

3）解决飞机上各成、附件的振动，有两种办法。一是改变其支持结构的振动频率，二是减小其振动量级，用大质量法计算振动频率对于解决工程上同类振动问题有一定的借鉴意义；

4）由于激励载荷的曲线假设为直线，与实际情况略有出入。如果激励载荷采用试验数据，用大质量法可以得到更准确的计算结果。

[1]张阿舟主编.实用振动工程（第一册）.北京：航空工业出版社，1996.

[2]Blakely Ken.Basic Dynamic Analysis，MSC/NASTRAN User's Guide Version 68.The MacNeal-Schwendler Corpora-tion，1993.

[3]李增纲.Nastran快速入门与实例.北京：国防工业出版社，2007.