一种基于 EMD和神经网络的超声缺陷信号分类方法✳

杨 录,樊建平,张艳花

(中北大学电子测试技术国家重点实验室,山西太原 030051)

缺陷特征提取是缺陷诊断的关键环节.在信号的时域图中,信号的幅值大小可以表征缺陷的存在.但是,只有信号时域幅值作为缺陷特征参数,它无法获得缺陷信号更多的真实信息,如缺陷的类型、大小等.因此,在超声无损检测领域,超声频谱分析法由于在频域中可以求得比时域更多的特征参数,如最大幅值、中心频率、带宽等,为提高检测结果的客观性和可靠性提供了可能[1-3].但是,当工件存在缺陷或其工作环境异常时,其相应的超声回波信号或振动信号一般呈非平稳特性.以傅里叶变换(Fourier Transform,FT)为核心的传统频谱方法虽然在平稳信号的特征提取中发挥了重要作用,但对于非平稳信号,FT只能分别给出信号在时域或频域的统计平均结果,却无法同时兼顾信号在时域和频域的全貌和局部化特征.因此,对于非平稳信号而言,希望能把非平稳信号分解,使非平稳信号平稳化,并能够得到比常规分析方法更多的缺陷特征参数,来最终达到识别缺陷类型的目的.下面将要介绍的经验模态分解(Empirical Mode Decomposition,EMD)[1,4]方法就可以很好地解决这个问题.

经验模态分解方法是基于信号的局部特征时间尺度,能把复杂信号函数分解为有限的固有模态函数 (Intrinsic Mode Function,IMF)之和,由于 EMD方法是依据信号本身的信息进行的分解,得到的 IMF通常是有限个数的,而且表现信号内含的真实物理信息[5],因此 EMD方法是自适应的信号处理方法,非常适合非线性和非平稳过程.

神经网络由基本神经元相互连接,能模拟人脑的神经处理信息方式,进行信息并行处理和非线性转换.神经网络是一种自适应的模式识别技术,并不需要预先给出有关模式的经验知识和判别函数,它通过自身的学习机制自动形成所要求的决策区域.它可以充分利用状态信息,对来自不同状态的信息逐一进行训练而获得某种映射关系.这种技术的出现,为故障诊断问题提供了一种新的解决途径.

本文将 EMD方法以及人工神经网络技术应用到超声缺陷信号的识别分类中[6],利用 EMD方法对超声回波信号进行分解,得到若干个 IM F,然后对包含故障信息的 IMF作时域与频域分析,构造特征向量,最后通过 BP神经网络作为诊断决策分类器来分类信号的缺陷类型.

1 EMD方法的基本原理

Hilbert-Huang变换方法由黄锷于1998年提出,EMD(经验模态分解)为其重要的组成部分.黄锷提出的 EMD方法可以很好地处理非平稳、非线性信号.这个方法不同于一些传统的方法,它是直观、直接、基于经验和自适应的.IMF是平稳的窄带信号,是原始信号在不同时间尺度上的信息,与原始信号相比 IM F分量相对简单得多,实际的时间序列往往信息成分比较复杂,弱信号往往被强信号成分或背景噪声所淹没,而这些小幅度信号可以在 IMF分量中较明显地表现出来.因此,对 IMF进行分析可以更准确有效地把握原始数据的特征信息.

经验模式分解的结果是一组 IMF,IMF满足两个条件:①在任意一点,函数极大值构成的上包络与极小值构成的下包络均值为零;②在整个数据段上,极值点(包括极大值和极小值)的数目与过零点的数目相等或至多相差 1.

经验模式分解算法的步骤包括:①求取信号x的所有极值点和过零点;②将所有极大值点用一条曲线连接起来,得到信号的上包络;用同样方法可以得到信号极小值点构成的下包络;③计算上包络和下包络的平均值,记为平均包络 m;④ 将信号减去平均包络 m,得到残余信号 r;⑤将 r作为信号重复以上过程,直到 r满足固有模态函数的条件为止,记为 IM F 1;⑥重复以上过程将信号分解为一组固有模态函数和一个残余信号之和.

2 基于 EMD的分析步骤

2.1 标准超声缺陷信号采集

这里采用有机玻璃作为标准试件,玻璃厚度为 6 mm,探头频率为 5 MHz,检测模式为爬波.作为标准的有机玻璃缺陷类型为上表面裂纹、下底面裂纹和板中央孔,如图1所示.这 3种缺陷的超声回波信号如图2所示.

2.2 标准缺陷信号的 EMD分解

首先针对下底面裂纹信号进行分析,对其它两种信号的分析采用同样的分析方法.用 EMD方法对下底面裂纹超声信号进行处理,得到一系列 IMF分量,如图3所示.IMF是平稳的窄带信号,是原始信号在不同时间尺度上的信息,每一个 IMF分量都是代表一组特征尺度的数据序列,具有实际的意义.

图1 缺陷实物图Fig.1 Standard flaw indications of Perspex

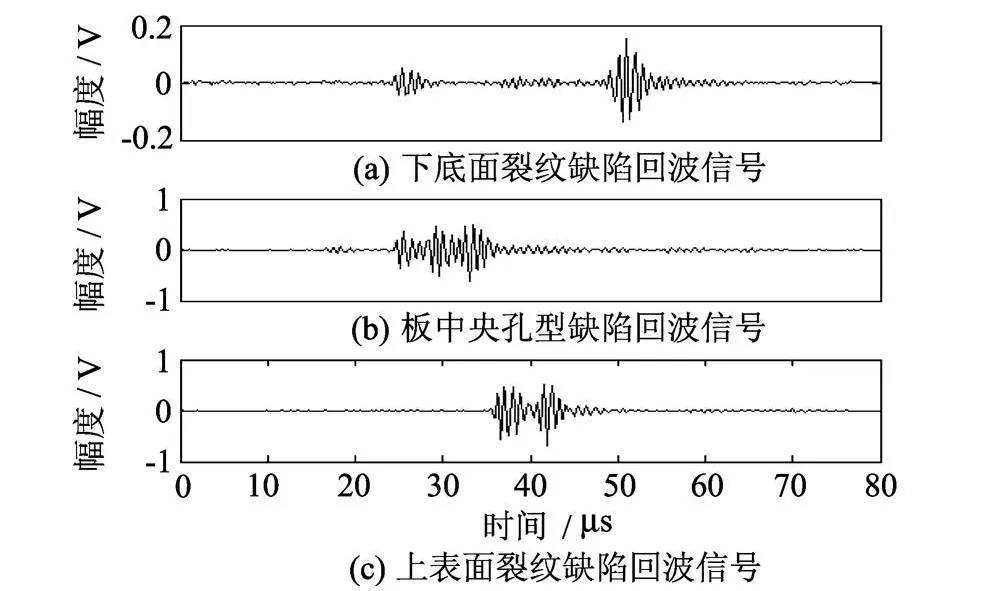
图2 3种标准缺陷超声回波信号Fig.2 Three kinds of ultrasound echo signals from standard flaw indications

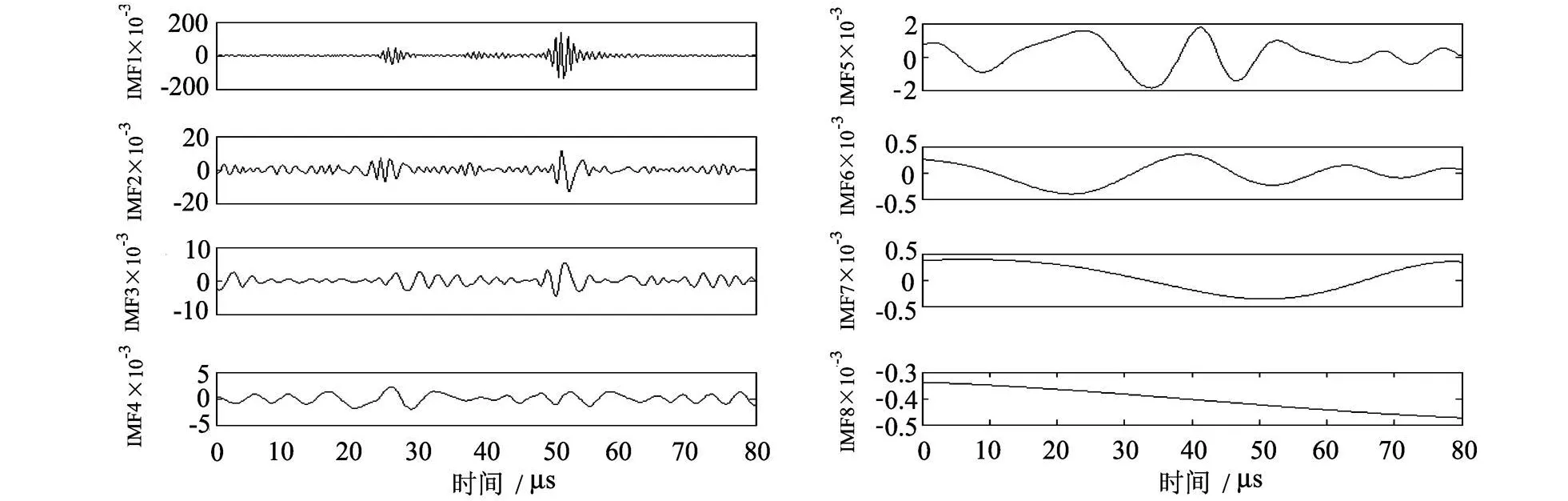
图3 下底面裂纹超声信号的 IMF分量Fig.3 Intrinsic modes IM F1～IMF8 of bottom surface flaw

2.3 IMF分量的分析

2.3.1 IMF的时域分析

对 IMF进行时域分析,采用过零点、信号面积、最大幅值这 3个特征参数作为 IMF曲线的时域特征[7].分别对每个 IMF分量求出曲线过零点、信号面积、最大幅值.对下底面裂纹信号的时域分析结果如表1所示(为便于分析,信号面积与最大幅值均放大若干倍数).

2.3.2 IM F的频域分析

对信号的各个 IMF分量进行傅立叶变换,得到如图4所示的幅频图.采用最大幅值、中心频率、信号能量这 3个特征参数作为 IMF的频域特征[7].分别对每个 IMF分量求出最大幅值、中心频率、信号能量.对下底面裂纹信号的频域分析结果如表2所示(为便于分析,最大幅值放大若干倍数).

表1 IMF时域特征参数计算结果Tab.1 IMFcharacterstic parameters in time domain

表2 IMF频域特征参数计算结果Tab.2 IM Fcharacteristic parameters in frequency domain

图4 各个 IMF幅频图Fig.4 Frequency spectrograms of IMFs

3 BP神经网络的基本原理及其输入向量的选取

3.1 BP神经网络基本原理

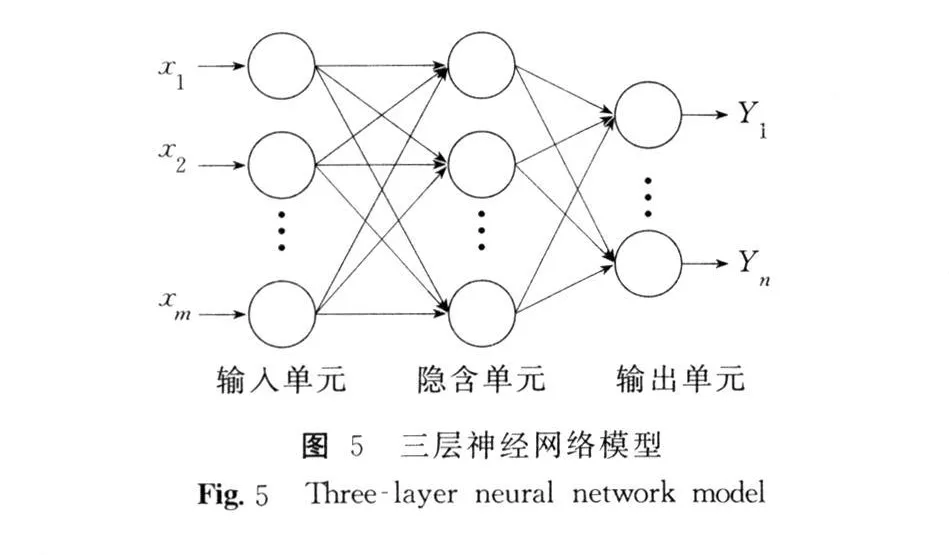
BP算法[8]的学习过程由信息正向传播过程和误差反向传播过程组成,在正向传播过程中,输入信息从输入层经隐含层单元逐层处理,并传向输出层,每一层神经元的状况只影响下一层神经元的状况.如果输出层不能得到期望的输出,则转入反向传播,将误差信号沿原来的连接通路返回,通过修改各层神经元的权值,最终使误差函数达到给定的数值.三层神经网络模型如图5所示.

3.2 BP神经网络输入向量的选取与处理

通过上述 IMF时域与频域的分析,每一个IMF分量可以得到过零点、信号面积、最大幅值(时域)、最大幅值(频域 )、中心频率、信号能量,共6个特征参数.把这些特征参数作为一个特征数组.下底面裂纹信号取前 5个 IMF分量,把 5个IM F分量的特征数组组合,就可以得到一个向量.这个向量即是信号的特征向量,把它作为神经网络的输入向量.

4 超声缺陷信号分类分析

针对标准的 3种缺陷信号进行采样,每种信号采集 30个样本,每个样本的数据长度为 400.试验时,对样本数据进行 N=5阶经验模态分解,利用本文分析得出的特征向量,每种样本取 6组特征向量,得到 18组数据,用这些数据作为训练样本输入网络进行训练.另外取 3种类型的信号各一个样本来作为测试样本,以检测所设计的缺陷分类器是否合理.

BP神经网络的具体结构[9]为:输入层神经元个数为 24,隐含层神经元个数近似为30,输出层神经元个数为 3.隐含层的传递函数采用双曲正切 S型传递函数 tansig,输出向量为故障编码 0,1,因此输出层的传递函数采用 S型的对数函数logsig,该函数将输出量的值域限制在 [0,1]之间.网络训练函数采用 Levenberg-Marquardt BP训练函数,性能指标为 mse,训练目标为 0.01.缺陷类别编码设计如表3所示.经归一化后的部分训练样本如表4所示.

网络的训练误差曲线如图6所示.从图6可以看出,经过此训练后达到了梯度最小值,此时的训练误差已经非常小.为了验证网络的准确性,用测试样本共9组数据对网络模型进行了测试,测试结果如表5所示.

从表5可以看出,网络的实际输出与期望输出非常吻合,诊断准确率为 100%,证明该神经网络模型可靠,能准确地对超声信号的缺陷类型进行识别与分类.

表3 缺陷类别编码设计Tab.3 Flaw type cod e design

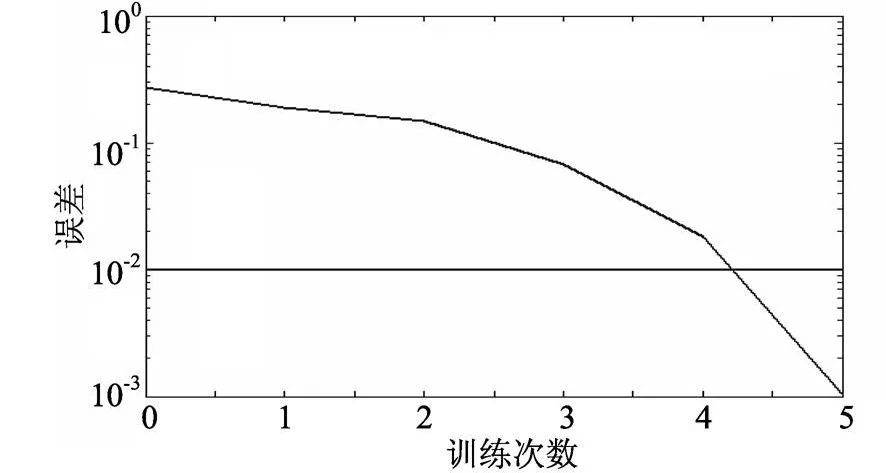
图6 训练误差曲线图Fig.6 Training error curve

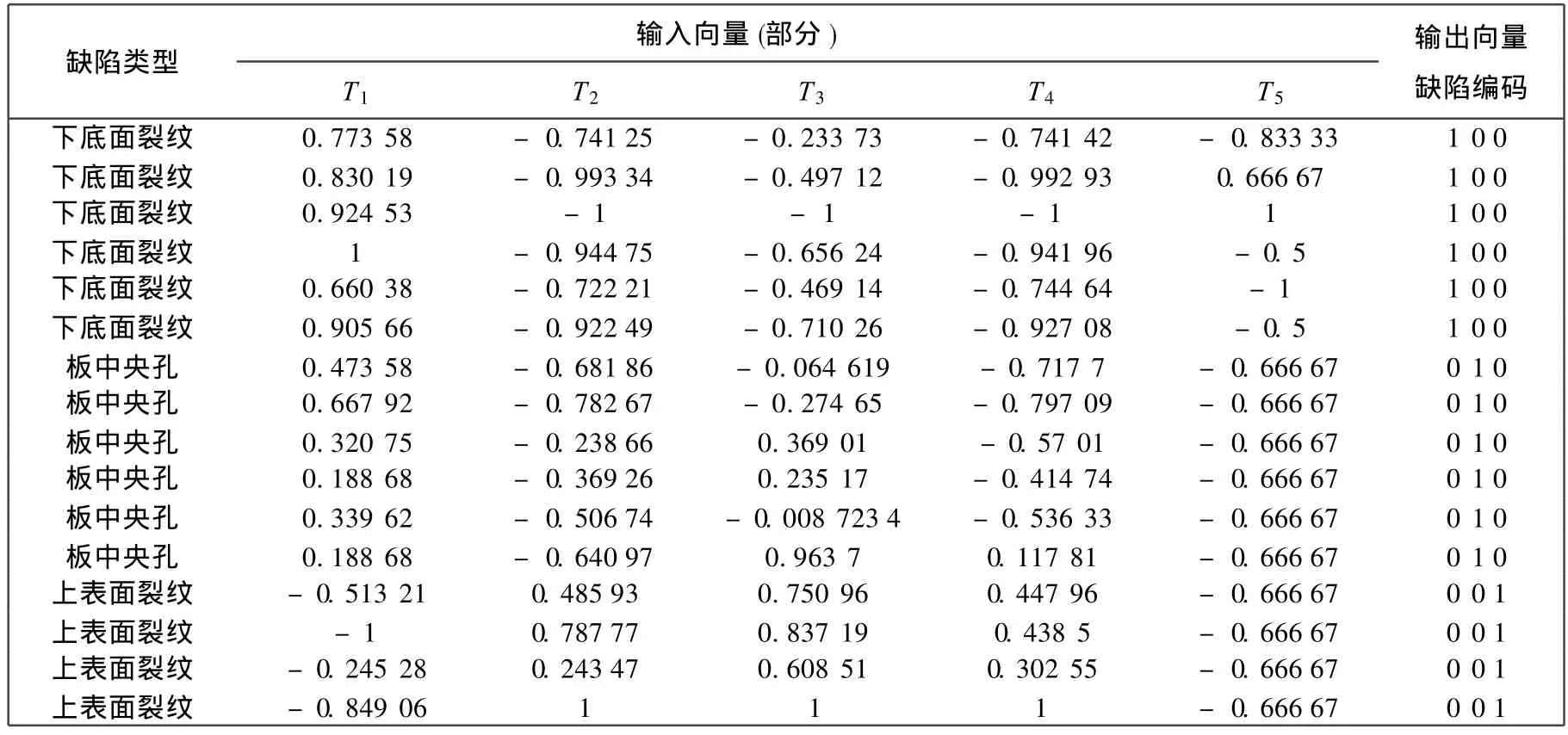
表4 归一化后部分训练样本Tab.4 Part training sample after normalization

表5 样本测试结果Tab.5 Sample test result

5 结束语

综上所述,基于对本征模函数时域与频域的分析[10],构造特征向量,利用神经网络分类信号缺陷类型是一种新的缺陷类型分类方法,其创新之处在于在分析本征模函数(IMF)时域与频域的基础上,构造特征向量,利用神经网络技术分类信号的缺陷.这种识别缺陷分类的方法识别率较高,可望具有较好的适用性.由于本文作为标准缺陷信号的缺陷类型较少,由此形成的特征向量能检测出的缺陷类型较少,因此,进一步应用需要大量的实验样本和数据分析.

[1]Huang N E.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[C].Lond: Proceedings of the Royal Society,1998,454:903-995.

[2]Bennett M,Michael S.Empirical mode decomposition and tissue harmonic imaging[J]. Ultrasound in Medicine&Biololgy,2005,31(8):1051-1061.

[3]Flandrin P,Rilling G,Goncalves P.Empirical mode decomposition as a filter bank [J]. IEEE Signal Processing Letters,2004,11(2):112-114.

[4]Deering R,Kaiser J.The use of a masking signal to improve empirical mode decomposition[J]. IEEE ICASSP,2005,9:485-488.

[5]于凤芹.利用 Hilbert-Huang变换的自适应带通滤波特性提取共振峰[J].声学技术,2008,27(2):266.Yu Fengqin.Finding speech formant by using the character of Hilbert-Huang transform as an adaptive band-filter[J].Technical Acoustics,2008,27(2):266.(in Chinese)

[6]张小蓟.基于 IMF能量熵的目标特征提取与分类方法[J].计算机工程与应用,2008,44(4):68-69.Zhang Xiaoji. Feature extraction and classification experiment based on energy entropy of IMF’s[J].Computer Engineering and Applications,2008,44(4):68-69.(in Chinese)

[7]孟宗,戴桂平.基于 EM D时频分析方法的性能研究[J].传感技术学报,2008,19(4):1029-1032.Meng Zong,Dai Guiping.Characteristics study on time-frequency anlysis method based on empirical mode decomposition[J].Chinese Journal of Sensors and Actuators,2008,19(4):1029-1032.(in Chinese)

[8]王宪保.基于仿生模式识别的构造型神经网络分类方法[J].计算机学报,2007,30(12):2109-2114.Wang Xianbao. Constructive neuron networks classification algorithm basedon biomimetic pattern recognition[J].Chinese Journal of Computers,2007,30(12):2109-2114.(in Chinese)

[9]夏战国,王珂.基于网络复杂性的 BP算法 [J].计算机工程与设计,2008,29(15):3867-3869.Xia Zhanguo,Wang Ke. BP algorithm based on network complexity[J].Computer Engineering and Design,2008,29(15):3861-3869.(in Chinese)

[10]钟佑明.希尔伯特-黄变换的统一理论依据研究[J].振动与冲击,2006,25(3):40-44.Zhong Youming.Uniform theory gist research of Hilbert-Huang transform[J].Journal of V bration and Shork,2006,25(3):40-44.(in Chinese)