开关磁阻电机线性模型的建模与仿真研究

俞枭辰，王家军

(杭州电子科技大学自动化学院，浙江杭州310018)

0 引言

开关磁阻电机综合了交流变频调速系统和直流调速系统的优良特性，被视为电气传动系统发展过程中的一个里程碑［1］。近年来，国外对开关磁阻电机的研究已从论证优点、开发应用阶段进入设计理论、优化设计阶段［2］，国内对开关磁阻电机的研究工作也正从摸索合理的设计方法发展为如何加速优化以进行开关磁阻电机的设计［3］。虽然开关磁阻电机的研究在国内外都取得了很大的发展，但作为一种新型调速系统，准确的仿真分析十分必要［4］。设计仿真的前提是将物理模型转化为数学模型，其中最简单的一种模型就是线性模型［5］，只要得到任意位置的电感值，就可以计算出磁链、转矩等。本文采用当前最常用的仿真软件MATLAB/Simulink搭建了开关磁阻电机的线性模型，并对其进行了仿真研究。

1 开关磁阻电机的线性模型

开关磁阻电机简称SRM，其运行机理与任何电磁式机电装置没有本质区别，都可以视为一对电端口和一对机械端口的二端口装置。对于任意相的开关磁阻电机，系统的微分方程描述可以由电路方程、机械方程、机电联系方程3部分组成。

在线性模型中，假设电机转速与电源电压恒定，不计磁路饱和影响，即绕组电感与电流大小无关，只和转子位置角有关，根据电路原理可以简化SRM第k相的电压平衡方程为:

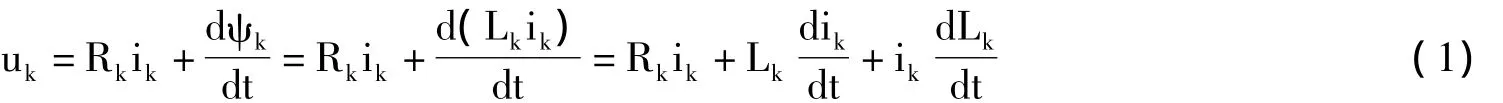
式中，uk，Rk，ik，(k和Lk分别为第k相的绕组电压、电阻、电流、磁链和电感，θ为转子位置角，ω为转子角速度。同时根据力学定律可以写出电机转子的机械运动方程为:

式中，Te为电磁转矩，TL为负载转矩，ω为转子角速度，F为阻尼系数，J为转动惯量。

SRM作为一种二端口装置，其电端口与机械端口是通过电磁转矩耦合在一起的，因此电磁转矩方程就表达了它的机电联系。在线性模型中，根据线性假设，单相电磁转矩方程可以简化为:

由式1、3可知在开关磁阻电机线性模型建模的过程中，最为关键的就是研究绕组电感L(θ)和转子位置角θ之间的关系。因为在SRM的线性模型中，只要得到任意位置的电感值，就可以根据uk、ik等可控变量和J、F结构参数等计算出SRM在任意时刻的转速、转矩等所有物理量。

开关磁阻电机的定子和转子都是凸极结构，如图1所示，其中βs，βr分别表示定子磁极极弧与转子磁极极弧。为简化计算，假设转子极弧等于定子极弧且小于转子槽宽，转子与定子磁极相对位置的变化会改变磁场分布，从而改变电感值。当转子凹槽中心与定子磁极轴线重合时相电感为最小值Lmin，当转子与定子磁极轴线重合时相电感为最大值Lmax。相电感的变化是周期性的，其周期为一个转子极距，即一个转子极弧加一个转子凹槽。在线性模型中，随着转子的转动，转子位置角θ不断变化，绕组电感就在最大值与最小值之间线性增减，如图2所示。

图1 三相6/4级开关磁阻电机

图2 线性模型中相电感L(θ)与转子位置角θ的关系曲线

在一个电感变化周期内，区间(θ1，θ2)内定子凸极一直与转子凹槽相对，相电感保持最小值;在转过θ2之后，定子凸极逐渐与转子凸极相对，相电感升高并且在θ3达到最大值;而在(θ3，θ4)内定子凸极逐渐与转子凸极相离，相电感降低并在θ4回到最低值，如此循环。所以相电感与转子位置角的关系为:

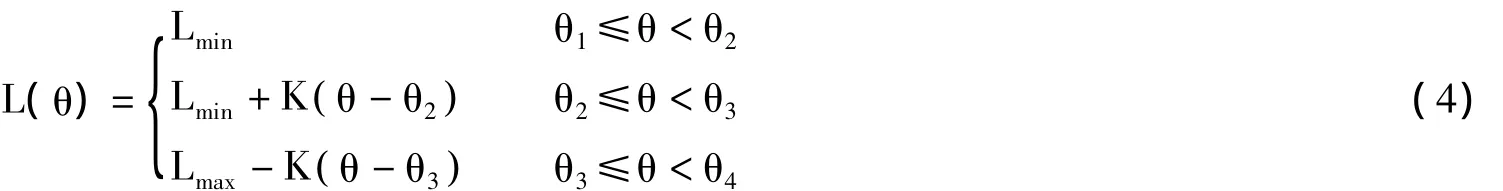
开关磁阻电机的激励控制策略有3种，分别为电流斩波控制、电压斩波控制和角度位置控制。本文的仿真模型采用电流斩波控制方式，因为该控制方式具有简单直接、可控性好等优点，避免了角度位置控制不适用于低速运动的问题也较电压斩波控制具有较小的开关损耗，是最为常见的控制方式。

电流斩波波形如图3所示，θon为开通角，是定子绕组接通电源瞬间定子和转子磁极的相对位置角，θoff为关断角，是定子绕组断开电源瞬间定子与转子磁极的相对位置角，Imax和Imin分别为电流斩波上限与下限。电流斩波控制通过对相电流与电流斩波上下限进行比较来达到对激励的控制，当θ处于电流导通区间(θon，θoff)内时，若 ik＜Imin，则主开关导通，ik逐渐上升至 Imax;反之若 ik＞Imax，则主开关关断，ik逐渐回落至Imin;如此反复，使得相电流始终在斩波限内波动。电流斩波控制适用于低速和制动运行下的SRM，可使电机获得恒转矩的机械特性，同时对限制SRM启动时的峰值电流有着显著的效果。

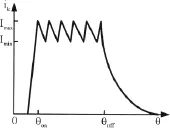
图3 电流斩波控制下的电流波形

2 基于Simulink的SRM线性模型建模

三相6/4级开关磁阻电机的线性模型在Simulink环境下的整体仿真结构如图4所示，Iref为给定的参考电流，Phase A、Phase B、Phase C为单相电路子模块，作用为通过参考电流Iref和转子位置角θ计算出三相的相电流，电感和转矩。将三相转矩合成即为电机的电磁转矩，根据式2求出转子角速度ω，ω经过积分环节后得到转子位置角θ作为3个单相电路子模块的输入。最后将A、B、C三相的电流和电感合成，并将角速度从rad/s转换为标准单位r/min后分别连接到相应示波器进行观察。

A相电路Phase A子模块的结构如图5所示，输入为参考电流与转子位置角，输出为相电流、电感和转矩。其中Modulo、Switch、Inductance和Torque这4个模块由MATLAB Function编写相应函数，其余功能都只需通过Simulink中的基本模块实现。

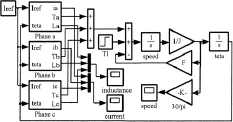
图4 线性模型整体仿真图

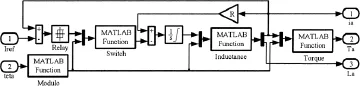
图5 A相电路Phase A子模块仿真图

滞环比较模块用以实现电流斩波控制，设滞环宽度为±ΔI，则电流斩波上下限分别为Imax=Iref+ΔI和Imax=Iref－ΔI，输出为电源电压Us，设置适当的滞环宽度即可对相电流ik进行精确的闭环控制。Modulo模块实现位置角归算功能，将输入的转子位置角与 /2求余，得到位置角在一个周期内对应参考零位置的值。Switch模块实现逻辑换相与功率变换功能，输入转子位置角与电源电压，根据电机三相的逻辑换相关系输出相电压uk。带饱和作用的积分模块用于计算磁链ψk，根据式1将相电压uk与相绕组电阻压降Rkik求差后积分即可求出磁链，积分环节的饱和作用是为了对输出的磁链值进行限幅，将其限定在要求的范围内。Inductance模块为相电流、电感计算模块，根据式4通过转子位置角计算当前相电感Lk，同时根据式1可知相电流ik=(k/Lk，所以由相电感和磁链可以很容易求得相电流。Torque模块为相转矩计算模块，根据式3通过转子位置角与相电流计算相转矩Tek。

3 SRM的PI控制仿真与分析

在基于Simulink的SRM线性模型建模的基础上加入PI控制器对转速进行闭环控制就得到了三相6/4级开关磁阻电机线性模型的PI控制仿真模型，如图6所示，其中PI控制器的输入为速度偏差，输出为电流参考值。仿真前先要对电机参数进行初始化赋值，如定、转子极弧，相绕组阻值，转动惯量，阻尼系数等，如表1所示。

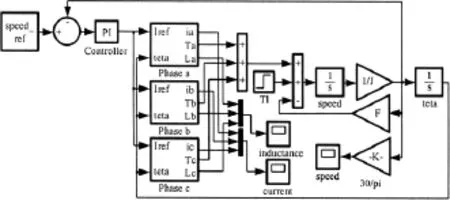
图6 三相6/4级开关磁阻电机线性模型PI控制仿真模型

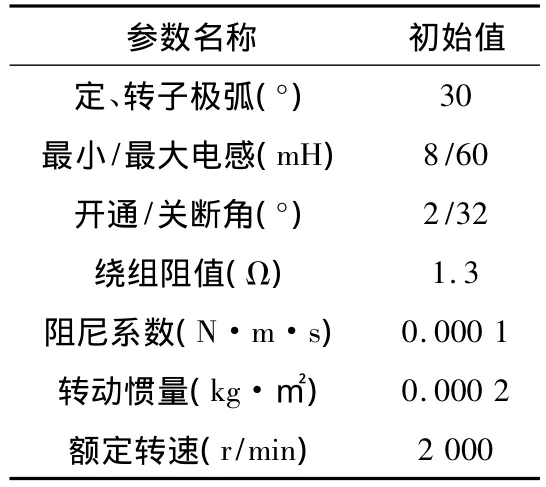
表1 初始化参数赋值

仿真结果如图7所示，将其与SRM线性模型理论进行比较可以发现，仿真结果与理论分析基本吻合，证明本仿真系统在PI控制策略下可以对SRM运行时的各种性能进行动态仿真。同时，本系统电感曲线完全线性化，速度响应准确，电流波形稳定则证明了本系统在电流斩波控制的滞环作用下性能良好，有一定的精度。

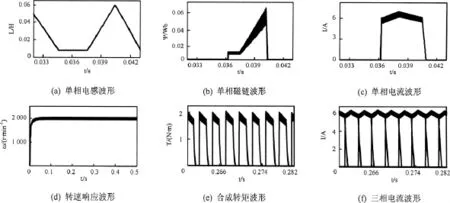
图7 PI控制下的仿真波形

4 结束语

本文给出了SRM的一种简单实用的建模方法，在MATLAB/Simulink环境下使用基本模块搭建了开关磁阻电机的线性模型仿真系统，利用本仿真系统可以对SRM的电流、转矩、转速等进行仿真，其结果可以为SRM控制系统的优化设计、优化控制、系统调试等提供参考，而MATLAB/Simulink这样高效、便捷的仿真工具无疑将使SRM的研究更加高效。

［1］孙建忠，白凤仙.特种电机及其控制［M］.北京:中国水利水电出版社，2005:86－89.

［2］Sorares F，Costa Branco P J.Simulation of a 6/4 Switched Reluctance Motor Based on Matlab/Simulink Environment［D］.Lisbon:Instituto Superior Tecnico，2001:5－12.

［3］吴建华.开关磁阻电机设计与应用［M］.北京:机械工业出版社，2000:7－11.

［4］Xiaoyan Wang.Modeling And Implementation Of Controller For Switched Reluctance Motor With Ac Small Signal Model［D］.Virginia state:Virginia Polytechnic Institute and State University，2011:15－20.

［5］吴红星.开关磁阻电机系统理论与控制技术［M］.北京:中国电力出版社，2010:110－112.