GRIDLESSMETHOD FOR UNSTEADY VISCOUSFLOWS
Pu Saihu,Chen Hongquan
(College of Aerospace Engineering,Nanjing University of Aeronautics and Astronautics,Nanjing,210016,P.R.China)
INTRODUCTION
Gridless method using clouds of points without requirement for a grid has become one of the hottest research areas in computational fluid dynamics.This new kind of numerical method provides another choice to solve partial differential equations besides mesh methods.It has also been used for simulating steady flows over complex boundaries[1-4].
Unsteady flows,such as deployment of high lift devices,deflection of control surfaces,and flutter of the wing,are very common in aeronautical area as well as steady flows.In recent years,many researches have focused on gridless method for unsteady flows simulation.Kirshman,et al[5]combined a Cartesian mesh and gridless boundary conditions with application to flutter prediction.Wang,et al[6]developed a gridless method for unsteady inviscid flow simulation.Wang,et al[7]introduced a new dynamic cloud method based on Delaunay graph mapping strategy.These previous studies were mainly concerned on unsteady invicsid flows.
However,for many aeronautical applications,the unsteady flows should not beviewed as invicsid because the computing results can not agree with the experimental data.On the contrary,they areviscous.Based on this knowledge,a novel gridless method is developed to solve unsteady viscous flows with moving boundaries.The present work includes three main aspects:(1)How to generate the point distribution for viscous flows simulation,(2)How to get the point distribution at each time-step since the boundary is moving,(3)How to discretize the spatial derivatives and temporal derivatives of the Navier-Stokes(NS)equations on the obtained points.To answer the first question,a hybrid point distribution strategy is proposed by considering the features of viscous flows.A fast moving technique of clouds of points at every time step is presented based on the attenuation law of disturbed motion aiming at the moving boundaries.The spatial derivatives of flow quantities are evaluated at each point with a weighted least-square curve fit method in its cloud of points.A 2-D unsteady compressible NScode is developed by incorporating all the aboveideas with the dual time stepping procedure.The code is validated by simulating the viscous flows passing a NLR7301 airfoil with an oscillating flap and a pitching NACA0012 airfoil.The numerical results are also presented.
1 GOVERNING EQUATIONS
The governing equations of the study are the compressible NS equations in Cartesian coordinates.The equations are written in the non-dimensional form[8]as

The NSequations arenon-dimensionalized by free stream density d∞ ,free stream pressure p∞ ,reference length L,and viscosity_∞ (Re∞ /(Ma∞ )) where Re∞ and Ma∞ represent the Reynolds number and Mach number of free stream.In Eq.(1),W is the vector of conservative variables,E and F the convective flux terms,E V and F V the viscous flux terms.The vector of conservative variables and the convective flux terms are given

where d,p,e are the density,pressure,and total energy per unit mass,respectively,u and v the Cartesian components of velocity vector,xt=d x/d t and yt=d y/d t the moving velocity components of the point,where d x,d y are the displacements of the point during the interval of time d t,U=u-xt,V=v-yt.For a perfect gas,the total energy per unit volume is where V is the ratio of specific heats of the fluid and typically set as V=1.4 for air.

The viscous flux terms E V and F V are given

where the viscous stress are


where_Lis the laminar viscosity coefficient which is computed with the Sutherland formula and_T the turbulence viscosity coefficient which is obtained from the Spalart-Allmaras turbulence model[9]. The Euler equations are obtained by setting the viscous fluxes equal to zero.
2 POINT DISTRIBUTION AND MOVING TECHNIQUE FOR CLOUD OF POINTS
In gridless method,the spatial derivatives of the governing equations are discretized in the cloud of points.Since viscous flows are simulated,the point distribution is implemented in an isotropic or anisotropic way according to the features of viscous flows.In the area far away from the body, the traditional cloud of isotropic points[2-3](Fig.1(a))is used,while in the adjacent area, the cloud of anisotropic points(Fig.1(b))is distributed.In this way,the point spacing normal to the wall is small enough for simulating the boundary layer while the total number of points in the computational domain is controlled due to the large spacing in other tangential direction through the anisotropic way.

Fig.1 Cloud C(i)for point i

Fig.2 Point distribution around NACA0012 airfoil
Fig.2 shows the point distribution around a NACA0012 airfoil obtained in the above way.This point distribution follows specific steps as:First,the airfoil and its wake region are wrapped in an envelope of points using the advancing-layers method[10]and the four neighboring points of each point obtained in this step are defined according to the layer structure(Fig.1(b)).Second,the remaining part of the flow field is filled with points by delaunay triangulation[11]and the neighboring points of each point obtained in this step are also defined(Fig.1(a)).It is obvious that when the advancing-layers method is implemented,the spacing normal to the wall can be easily controlled.In Fig.2,the first point spacing normal to the wall is specified at 5×10-5.
In unsteady flow computation,that clouds of points can move with the body boundaries is required to simulate the relative movement of body boundaries.Hence,a fast moving technique of clouds of points is used.The technique first proposed by Lu[12]for thedynamic structured grids is based on theattenuation law of disturbed motion.Here the technique is developed for the dynamic cloud of points by some modifications.The details of the technique are described as follows by taking the incompressible potential flow round a cylinder for example.
The stream function is

where a is the radius of the cylinder,V∞the velocity of free stream.Magnify the cylinder′s radius to a+X,then the previous streamline passing point(r,θ)yields a normal displacementΔr

It is difficult to generate dynamic grids using Eq.(7)directly.By further simplification,the coordinates(represented by subscript t)of the dynamic grids are

where subscript r is the instantaneous coordinate which the static grids move to with bodies,s the boundary-fitted static grids used as initial values,g the function for the serial number of the grid line

where i,j are the serial numbers of each point."b"is the corresponding boundary points and"f"the far field points.In the method,the new coordinates of each grid point are obtained directly by Eq.(8)without iteration.It is an efficient way for grid point moving.In fact,the method was successful in generating dynamic structured grids for the control surface moving and the wing flutter[8].There is no serial number of each point in gridless method as that in structured grid,so Eq.(9)can not work in gridless method.Therefore,g is changed into where d is the distance between point i and the surface of the body,dfthe distance between point i and the far-field boundary.When the body moves,the new coordinates of each gridless point are also obtained directly by Eq.(8),and for each point,the topology of its clouds is not changed.Fig.3 shows the point distribution when the airfoil rotates 30°about 25% of the chord on the basis of Fig.2.The moving scale of the surface is very large but the point distribution mainly keeps the same quality as that of the initial point distribution adjacent to the wall,which profits the simulation of the boundary layer.

Fig.3 Point distribution around NACA0012 airfoil after rotating
3 NUMERICAL DISCRETIZATION OF GOVERNING EQUATIONS
3.1 Spatial discretization
For gridless method,the spatial derivatives of any quantities are evaluated through linear combinations of certain coefficients and the quantity of the cloud of points.For example,in the cloud of points C(i)(Fig.1),the first spatial derivatives of function f at point i are evaluated with the following linear combination forms[2]

where m is the number of neighboring points of point i in the cloud of C(i),and f ik the value at the midpoint between points i and k.The coefficients T ik and U ik are obtained with a weighted least-squares curve fit to the following linear equation[4]

The weight functions used in this study are

where rk is the relative distances defined as
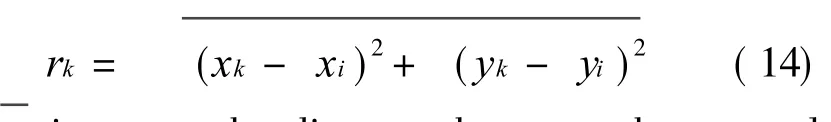
where riis set as the distance between the central point to the nearest point in its cloud of points.
Eq.(11)is applied to the convective flux of the NSequations to obtain the following expression

The numerical flux G ik at the midpoint between points i and k is obtained using Roe′s approximate Riemann solver[2].
The viscous terms of the NS equations are evaluated at each point

where the first spatial derivatives is obtained by Eq.(11)directly,while the second derivative is obtained by

The first derivative at the midpoint between points i and k is obtained as[4]

whereΔx,Δy,andΔs2are given as

After the spatial discretization,the semi-discretization form of the NSequations on point i is

3.2 Temporal discretization
Second-order backward difference method is implemented to the temporal derivatives of Eq.(20)as

whereΔt is theglobal physical time step.A timestepping methodology[13]is used to solve Eq.(21)to form the derivative term of conserved variables with respect to pseudo-time f

The unsteady residual is defined as

Eq.(22)is reformed as

Then,the four-stage Runge-Kutta algorithm is used to solve Eq.(24)with the local time-stepping and residual averaging for accelerating[13].For theviscous flows,no-slip boundary condition is imposed on the wall.In th e far field,one dimensional characteristic analysis based on Riemann invariants is used to determine the values of the flow variables on the outside of the boundaries in the computational domain.
4 NUMERICAL RESULTS
In this section,the accuracy of the presented spatial discretization is firstly evaluated by the steady flow calculation on subsonic and transonic viscous flows around a NACA0012 airfoil.Then the unsteady flows around a NLR7301 airfoil with an oscillating flap and a pitching NACA0012 airfoil are simulated respectively.
4.1 Steady viscous flow around NACA0012 airfoil
Viscous flows over a NACA0012 airfoil were experimentally studied by Thibert et al[14].To validate the present gridless method two test cases with different conditions are conducted:one is obtained at a free stream with Mach number of 0.5,an attack angle of 3.51°,and the Reynolds number of 2.93×106(Fig.4(a)),the other is obtained at a free stream with Mach number of 0.754, an attack angle of 3.02°, and the Reynolds number of 3.76×106(Fig.4(b)).The obtained pressure distributions on the airfoil surface are compared with the experimental data(Fig.4),which indicates a good agreement between the numerical results of the proposed gridless solver and the experimental data.And from the view of these two cases,the accuracy of the present spatial discretization method is satisfactory.

Fig.4 Surface pressure comparisons
4.2 Unsteady viscous flow around NLR7301 airfoil with oscillation flap
The test of the unsteady viscous flow around a NLR7301 airfoil is conducted.The part of airfoil surface before 75% of the chord stands still while the other part has an oscillation flap.The axis of the flap is located at 75% of the chord,the angle is set as W(t)=0.03°+ 0.97°sin(k t),and the reduced frequency is k=k c/2U∞=0.071,where c represents the chord length and U∞the free stream velocity.The free stream Mach number is 0.701,the attack angle of the airfoil is 3°,and the Reynolds number is 2.14×106.To observe the in fluenceof viscous effect,the NSequations and the Euler equations are solved by using the initial point distribution with the point spacing normal to the airfoil of 5×10-5(Fig.5)and 5×10-3,respectively.

Fig.5 Point distribution around NLR7301 airfoil
Fig.6 shows the stream lines when the trailing-edge flaps at the angle:W(t)=1.0°.There is a separatevortex at the upper surface of the trailing-edge.Figs.(7-9)show the obtained distribution of different parts of the unsteady pressurecoefficient. The pressure distributions obtained from the Euler equations do not agree well with the experimental data[15],while those obtained from the NS equations concerning the viscous effect are much more close to the experimental data.Therefore,the NSequations are more suitable to solve this case.In addition,if laminar NS is applied,the solver can not even converge at every time step because the Reynolds number is as large as 2.14×106.Thus the effect of turbulence should be taken into account.

Fig.6 Stream lines near trailing-edge

Fig.7 Distribution of mean part of p

Fig.8 Distribution of real part of p

Fig.9 Distribution of imaginary part of p
4.3 Dynamic stall on pitching NACA0012 airfoil
In this case,a NACA0012 airfoil is pitching at 25%of the chord with theattack angle:T(t)=6.25°+ 8.5°sin(k t),and the reduced frequency k=k c/2U∞=0.075 where c represents the chord length and U∞the free stream velocity.The free stream Mach number is 0.4,and the Reynolds number is 3.4×106.

Fig.10 Stream lines at different angles of attack
Numerical results are obtained by solving the NS equations and the initial point distribution is shown in Fig.2.Fig.10 presents the stream lines when the instantaneous attack angles are 14.75°(maximum angle)and-2.25°(minimum angle).In Fig.10,when theinstantaneous attack angleis 14.75°,there are three vortexes near the upper surface,while the stream flows along the surface smoothly when the instantaneous attack angle is-2.5°.In the whole cycle of the pitching,the flow features has a large range of change.Figs.(11-12)show the unsteady lift and moment coefficients versus the instantaneous attack angle respectively.Numerical prediction of the present gridless method are compared with the experimental data[15]and the results in Ref.[16],which achieves good agreement.

Fig.11 Lift coefficient versus angle of attack

Fig.12 Moment coefficient versus angle of attack
5 CONCLUSION
With concerning point distribution in an isotropic or anisotropic way,gridless method is successfully implemented for the NS equations.Theverified numerical results show that themoving technique of clouds of points based on the attenuation law of disturbed motion can be easily applied for two-dimensional unsteady viscous flows involving moving boundaries.To simulate the unsteady flows involving large-scale moving boundaries,some modifications including the reconstruction of the structure of some clouds are required,and the relevant research isin progress.
[1] Batina JT.A gridless Euler/Navier-Stokes solution algorithm for complex aircraft applications[R].AIAA 93-0333,1993.
[2] Chen H Q,Shu C.An efficient implicit mesh-free method to solve two-dimensioanl compressible euler equations[J]. International Journal of Modern Physics C,2005,16(3):439-454.
[3] Katz A,Jameson A.Edge-based meshless methods for compressible flow simulations[R].AIAA 2008-699,2008.
[4] Morinishi K.Gridless type solver-generalized finite difference method[J].Notes on Numerical Fluid Mechanics,2001,78:43-58.
[5] Kirshman D J,Liu F.Flutter prediction by an Euler method on non-moving Cartesian grids with gridless boundary conditions[J].Computers&Fluids,2006,35:571-586.
[6] Wang G,Sun Y,Ye Z.Gridless solution method for two-dimensional nsteady flow[J].Chinese Journal of Aeronautics,2005,18(1):8-14.
[7] Wang H,Chen H,Ma Z,et al.Gridless method for solving moving boundary problems and its dynamic cloud points[J].Journal of Nanjing University of Aeronautics& Astronautics,2009,41(3):296-231.(in Chinese)
[8] Guo T.Transonic unsteady aerodynamics and flutter computations for complex assemblies[D].Nanjing:Collegeof Aerospace Engineering,Nanjing University of Aeronautics and Astronautics, 2006. (in Chinese)
[9] Spalart P R,Allmaras S R.A one-equation turbulence model for aerodynamic flows[R].AIAA-92-0439,1992.
[10] Pirzadeh S.Three-dimensional unstructured viscous grids by the advancing-layers method[J].AIAA Journal,1996,34(1):43-49.
[11] Weatherill N P.Delaunay triangulation in computational fluid dynamics[J].Computers&Mathematics with Applications,1992,24(5):129-150.
[12] Lu Z.Generation of dynamic grids and computation of unsteady transonic flows around assemblies[J].Chinese Journal of Aeronautics,2001,14(1):1-5.
[13] Blazek J.Computational fluid dynamics:Principles and Applications[M].Amsterdam:Elsevier Science Ltd publisher,2001:171-173.
[14] Thibert J J, Granjacques M, Ohman L H.NACA0012 Airfoil[R].AGARD AR 138,1979.
[15] Lambourne N C,Landon R H,Zwaan R J,et al.Compendium of unsteady aerodynamic measurements[R].AGARD Report 702,1982.
[16] Kerho M.Adaptive airfoil dynamic stall control[R].AIAA 2005-1365,2005.
 Transactions of Nanjing University of Aeronautics and Astronautics2012年1期
Transactions of Nanjing University of Aeronautics and Astronautics2012年1期
- Transactions of Nanjing University of Aeronautics and Astronautics的其它文章
- NOVEL WEIGHTED LEAST SQUARESSUPPORT VECTOR REGRESSION FOR THRUST ESTIMATION ON PERFORMANCE DETERIORATION OF AERO-ENGINE
- APPLICATION OF HYBRID AERO-ENGINE MODEL FOR INTEGRATED FLIGHT/PROPULSION OPTIMAL CONTROL
- LINEAR ULTRASONIC MOTOR USING LONGITUDINAL VIBRATION
- VIBRATION CHARACTERISTIC INVESTIGATION OF COUNTER-ROTATING DUAL-ROTOR IN AERO-ENGINE
- CNC SYSTEM OF FLEXIBLE FIXTURE IN AIRCRAFT COMPONENT MANUFACTURING AND ASSEMBLY
- EXPERIMENTAL STUDY OF HTC FOR FILM COOLING OF PARALLEL-INLET HOLES
