NOVEL WEIGHTED LEAST SQUARESSUPPORT VECTOR REGRESSION FOR THRUST ESTIMATION ON PERFORMANCE DETERIORATION OF AERO-ENGINE
Su Weisheng,Zhao Yongping,Sun Jianguo
(1.Aviation Motor Control System Institute,Aviation Industry Corporation of China,Wuxi,214063,P.R.China;2.ZNDY of Ministerial Key Laboratory,Nanjing University of Science and Technology,Nanjing,210094,P.R.China;3.College of Energy and Power Engineering,Nanjing University of Aeronautics and Astronautics,Nanjing,210016,P.R.China)
INTRODUCTION
In the past few years,National Aeronautics and Space Administration(NASA)has made great efforts to develop advanced aero-engine control concepts,which has been confirmed in many articles[1-4].Among these advanced concepts,intelligent engine control(IEC)has drawn much attention since it was proposed by Adibhatla et al[5].Up to now,IEChas involved many contents including model-based control[6],life extending control[7],performance deterioration mitigating control (PDMC)[8-10]. PDMC shows great promise to accommodate future aero-engines with many advantages including:(1)PDMC can reduce the control dependency on human and realize autonomous operation of the propulsion system by keeping the relationship between power lever angle(PLA)and engine thrust stand still while engine performance deteriorating due to wear.(2)Compared with traditional control methodology,PDMC can achieve the direct control of engine thrust and the unmeasured variable of interest,resulting in less conservative designs which can lengthen engine life and improveoperating efficiency.(3)If all the engines on a multi-engine aircraft do not have the same throttle-to-thrust relationship,a thrust imbalance will occur,causing unwanted yaw which requires pilot intervention.PDMCcan avoid this.
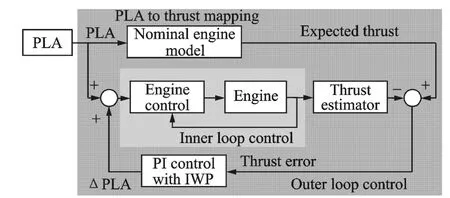
Fig.1 PDMCarchitecture
PDMC consists of two parts:the inner loop control,namely the traditional control methodology for aero-engines,and an additional part,the outer loop control(Fig.1).Because of outer loop control,PDMC always keeps the same throttleto-thrust relationship without considering the engine performance deterioration.Meanwhile,it can avoid unwanted yaw caused by thrust imbalance.To implement PDMC,more emphases are put on outer loop control because the inner loop control involves the standard engine controller like a full authority digital engine controller(FADEC).Obviously,the outer loop control is comprised of three components:nominal engine model,proportional-integral(PI)controller with integrator windup protection(IWP),and thrust estimator.Nominal engine model only plays a role in PLA for thrust mapping to obtain the expected thrust as a reference signal.PI controller produces the incremental value of PLA(ΔPLA)via the thrust error to modify the input of PLA command implicitly. The third component,thrust estimator,is used to estimate the current thrust of enginein time.Unlike PIcontroller,the design of thrust estimator seems more difficult.By now,th rust estimator can be realized in two ways.One is the implementation using the conventional numerical methods,i.e.Kalman filter[11].Since machine learning theory emerged,thrust estimators based on it like neural networks and support vector machine(SVM)have attracted great attention recently[12-14].But the study is still on the inchoate stage.Most of the machinelearning-based thrust estimators only focused on thrust estimation without concerning performance deterioration.In this study,research on thrust estimator of performance deterioration on the basis of machine learning theory,least squares support vector regression(LSSVR),is conducted to meet the need of PDMC.
SVM[15-16]has prevailed in many fields since it was proposed.Unlike artificial neural network(ANN)which easily fits in local solution,SVM owns a unique global optimization solution with unacceptable training cost for large scale problems,because the training complexity rises geometrically with theincrease of the size of training samples.To lessen the training burden,LSSVR was proposed by Suykens,et al[17]to cope with quadratic programming problem in SVM by a linear equation as a surrogate.However,the lack of sparseness and robustness[18]was brought out while using the equality constraints instead of inequality ones and replacing the X-insensitive loss function by the squared loss function.To overcome those disadvantages,the pruning strategy[19]was proposed by reducing the number of support vectors to shorten the prediction time and enhance the real-time performance.Meantime,the weighting strategy was proposed to enhance the robustness of LSSVR[18],butit did not satisfy all the settings. For example,the weighting strategy in thrust estimator reduced the estimation effectiveness because of its unsuitability.That is to say,the weighting strategy should be adopted appropriately according to the actual settings.Therefore a novel weighting strategy is proposed to improve the robustness of LSSVR while reserving good performance of thrust estimation on the basis of exhaustive analysis of the mentioned references.Finally,the experiments on a nonlinear component level model of dualspool turbofan engine with mixing exhaust validate the effectiveness and feasibility of the proposed weighting strategy.
1 WEIGHTED LEAST SQUARES SUPPORT VECTOR REGRESSION
Before the introduction of weighted least squares support vector regression(WLSSVR),the normal LSSV Ris firstly described.A training data set{(xi,di)}Ni=1 with a size N is given in the normal LSSV R,where xi is theinput variableand di the output variable with the value predicted from the value of xi.The normal LSSVR is to find the normal vector w and thebias b so that for each sample(xi,di),the affine function f(xi)=wTxi+b yields a small deviation between the ob-served valve di and the predicted value f(xi).The parameters can be obtained by solving the following optimization problem that the model complexity pluses thesquared training errors with equality constraints
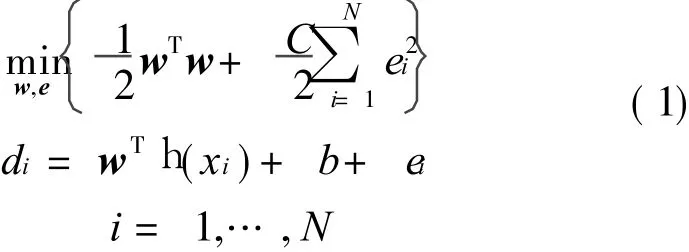
where e=[e1,e2,… ,eN]T,h(◦ )is a nonlinear mapping which can transform the input data xi in the input space into h(xi)in the feature space,C>0 the regularization parameter which can control the tradeoff between theflatness of the model and closeness to the training data.Because some samples contributs more than others while obtaining f(x),a weighting factor vi(i=1,…,N)is introduced to form the optimization problem
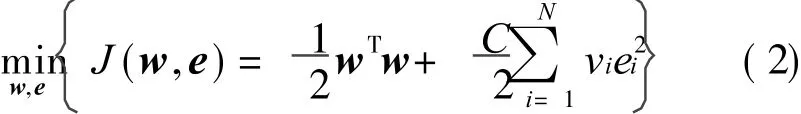
d i=wTh(xi)+ b+ei i=1,…,N
Lagrangian function is constructed to solve Eq.(2)as
L(w,b,e;T)=J(w,e)-
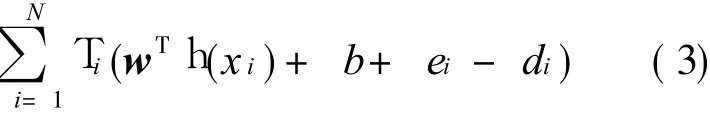
where T=[T1,…,TN]Tis the Lagrangian multiplier vector.According to the Karush-Kuhn-Tucker(KKT)condition of Eq.(2),we have
After eliminating w and ei,the following equation set is obtained
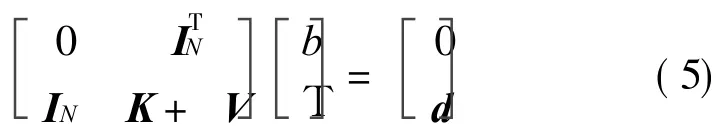
where d=[d1,d2,… ,dN]T,IN=[1,… ,1]T,K
N is a kernel matrix with the elements Kij=k(xi,xj)=h(xi)Th(xj),V=the diagonal matrix,k(◦ ,◦ )the kernel function.Among many kernel functions the Gaussian kernel function k(xi,xj)=exp(- ‖ xi-xj‖2/2V2)is commonly used with a tuning parameter V.After solving Eq.(5), the prediction function of WLSSVR is obtained
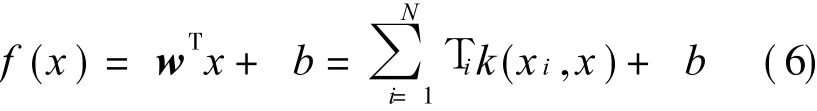
Therefore,Suykens,et al[18]gave a scheme of robust estimates to determine the weighting factor vi(i=1,…,N)by formulating
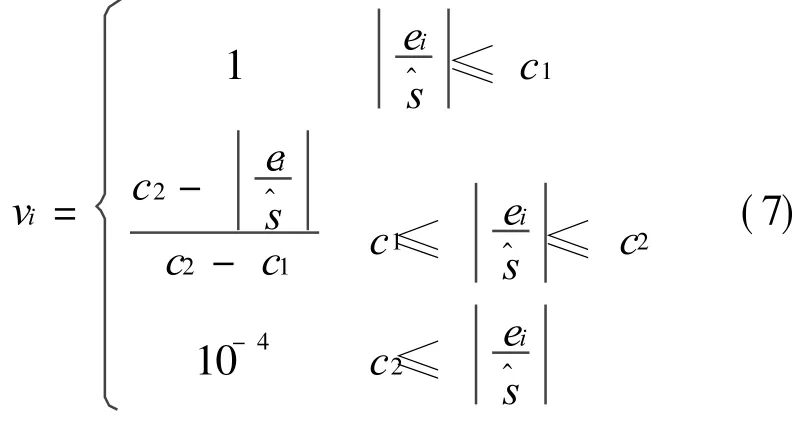
where s^is a robust estimate of the standard deviation of the normal LSSV R error variables ei
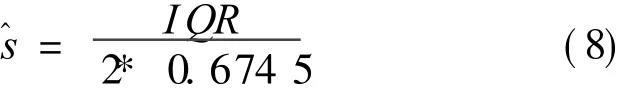
where IQR is the inter-quartile range,the difference between the 75th percentile and 25th percentile.During the estimation of^s,how much the estimated error distribution deviates from a Gaussian distribution is taken into account.The constants c1 and c2 are typically chosen as c1=2.5 and c2=3.From the experimental results given by Suykens et al,this weighting scheme can improve the robustness of normal LSSV R due to the involvement of squared errors loss function.In addition,the weighting factor vi is estimated from a statistical viewpoint.When the training sample x i induces a large training error,i.e.its corresponding,theweighting factor is endowed with a very small number as 10-4.In other words,the contribution made by sample xi to the final target function is negligible.However,in some situations wheremore emphases are required to put on the training samples inducing large training errors,the weighted strategy proposed by Suykens,et al is inappropriateobviously because the modeling effectiveness may be notimproved and even become worse.It is necessary to propose an appropriate weighting strategy to adapt the design of thrust estimator.In this situ-ation,a new weighting strategy is proposed as
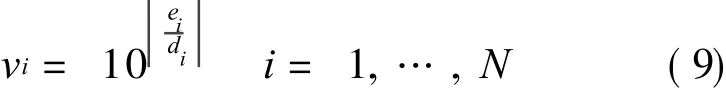
According to Eq.(9),the larger relative training error the training sample induces,the more weighting factors are given.The presented weighting strategy is more suitable for the design of thrust estimator than Suykens,et al′s because more emphases are put on the training samples producing larger relative training errors.The experimental results in section 2 will support it.
It is not enough to design thrust estimator using WLSSVR,since according to Eq.(6)every training sample is a support vector,which limits the real-time performance.The prediction time is in direct proportion to the number of support vectors.Suykens,et al proposed a pruning method as imposing sparseness to prun support values from the sorted support value spectrum. The complete reduction strategy is executed by using this method because if a training sample is pruned,it is completely discarded to retrain WLSSVR.According to Eq.(2),every training sample is a support vector in WLSSVR.Those so-called non-support vectors are imposed and every training sample makes its own contribution to WLSSVR.However,if every training sample is retained as support vector,the real-time performanceof WLSSVRwill be limited.As a tradeoff,during implementing the pruning method,the partial reduction[20-21]is employed to reduce the number of support vectors and enhance the realtime performance while considering the effects of the pruned training samples on the final WLSSVR.Eq.(5)is unfolded as
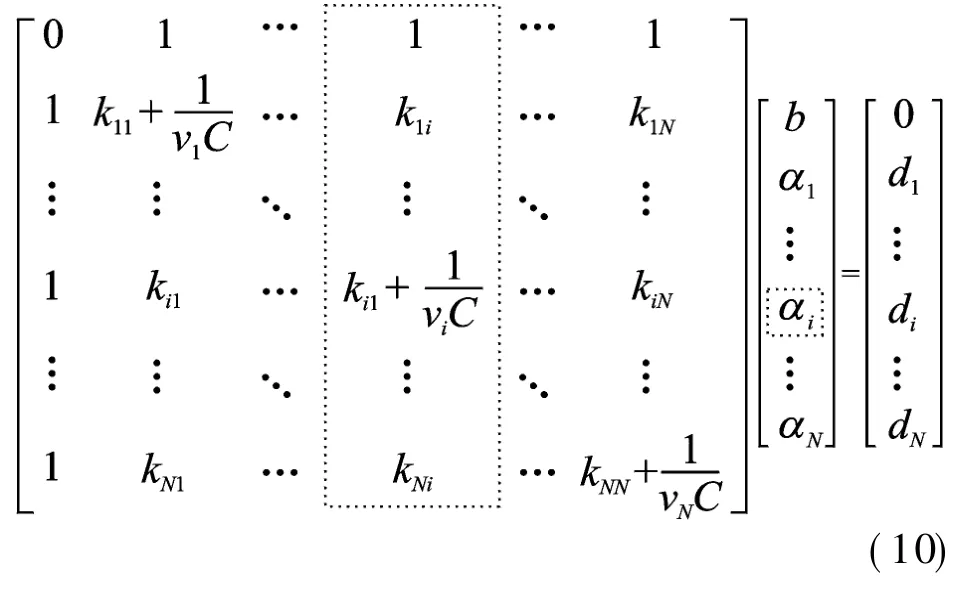
If xi is chosen as non-support vector and pruned,only its corresponding column (the dashed box in Eq.(10)is removed without deleting the corresponding row.Hence,an over-determined linear equation set is obtained as

where K~is equal to the matrix(K+V)without the column corresponding to the sample xi,T~=[b,T1,…,Ti-1,Ti+1,…,TN]T,d~=[0,d1,…,dN]T.Generally,Eq.(11)is solved in the least squares sense.It is well-known that the solution to Eq.(11)satisfies the following normal equation

where~ KT~ Kis theinformation matrix,whose condition number is double that of~ K.If Eq.(12)is solved directly,the obtained~Tbecomes bad due to large rounding errors.Instead,QR decomposition with pivoting,a very stable algorithm,is used to solve Eq.(11)in the least squares sense.It is easy to realize with backslash operator in Matlab.The proposed pruned WLSSVR is summarized as follows.
Algorithm 1:the proposed pruned weighted LSSVR(Z-WLSSVR)
Step 1:Initialize the kernel parameter V,the regularization parameter C,the weighting factor
Step 2:Construct Eq.(5)with violdand solve it.
Step 3:Calculate the predefined performance index.If the performance index degrades,stop,else sort the support values|T i|.And choose a small amount of training samples with smallest support values and remove their corresponding columns from Eq.(10).
Step 4:Compute theweighting factors vniewof the remaining training samples according to Eq.(9),where
Step 5:Set v iold=v iold◦ v inew,update the weighting factors in Eq.(11)with voild,solveit by using the QR decomposition,and then go to Step 3.
2 EXPERIMENTS
The proposed Z-WLSSVR with the advantages of effectiveness and feasibility is applied to design thrust estimator for PDMC.All the experiments in the study are carried out by Matlab 2007a on a personal computer with Intel(R)CoreTMi7 CPU 950 processor and Windows XPoperation system.The research object is a nonlinear component level model(CLM)of dual-spool turbofan engine with mixing exhaust(Fig.2).For convenient comparison and measuring,a performance index RD,relative deviation,is defined as
where diis the measured value,f(xi)the predicted value.

Fig.2 Illustration of dual-spool turbofan engine with mixing exhaust
Z-WLSSVR is firstly used to design thrust estimator for PDMC. Then Suykens,et al′s pruned LSSV R(S-LSSVR)is also utilized to demonstrate the irrationality of Suykens,et al′s weighting strategy in this setting.For a fair comparison,all algorithms are initialized with the same model parameters:the kernel parameter V and the regularization parameter C,determined by cross validation technique[22]with normal LSSVR.In the experiments,the performance deterioration of four components including fan,compressor, high-pressure turbine, and lowpressure turbine is considered with the efficiency degradation ranging from 0%—5%.The PLA scales in the closed interval[25°,110°].When PLA is set beyond 75°,the afterburner starts to work.As for the input variables,according to Ref.[13],seven measurements are selected including the altitude(H),Mach number(Ma),the total pressure of the outlet of bypass(P16),the total temperature of section 8(T 8),the temperature ratio of aero-engine(ETR),the main fuel flow (WFB),and afterburner fuel flow(WFA).These input variables are normalized within the range of[0,1]beforeinput into thrust estimator because of their different measurements.The experimental results on four flight conditions using the proposed Z-WLSSVR are drawn in Fig.3.Duo to the space limitation,simulations with other algorithms,including normal LSSVR[17],S-LSSVR[19],S-WLSSVR[18],and ZWLSSVR,are not mentioned here but the detailed results are listed in Table 1.
According to Fig.3,the maximum of theabsolutevalue of RD is not more than 3.5‰,which satisfies the requirement of PDMC.When normal LSSVR is used to design thrust estimator,the prediction time is the longest,usually more than 2 ms,which does not meet the requirement of designing aero-engine controller.Hence,S-LSSVR is employed to cut down the prediction time with the enhancement of the real-time performance through reducing the number of support vectors.S-WLSSVR is also utilized to model thrust estimator to further increase real-time performance.Due to the inappropriate weighting strategy,the real-time performance is not improved under the last threeflight conditions.The prediction timeis shortened obviously by Z-WLSSVR compared with S-LSSVR,which saves more time for engine controller.Because of the success of constructing thrust estimator for PDMC,the effectiveness and feasibility of the proposed Z-WLSSVR are confirmed. Meantime,the appropriate weighting strategy should be applied according to the actual settings.
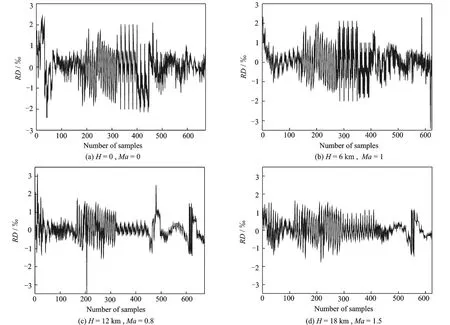
Fig.3 Experimental results
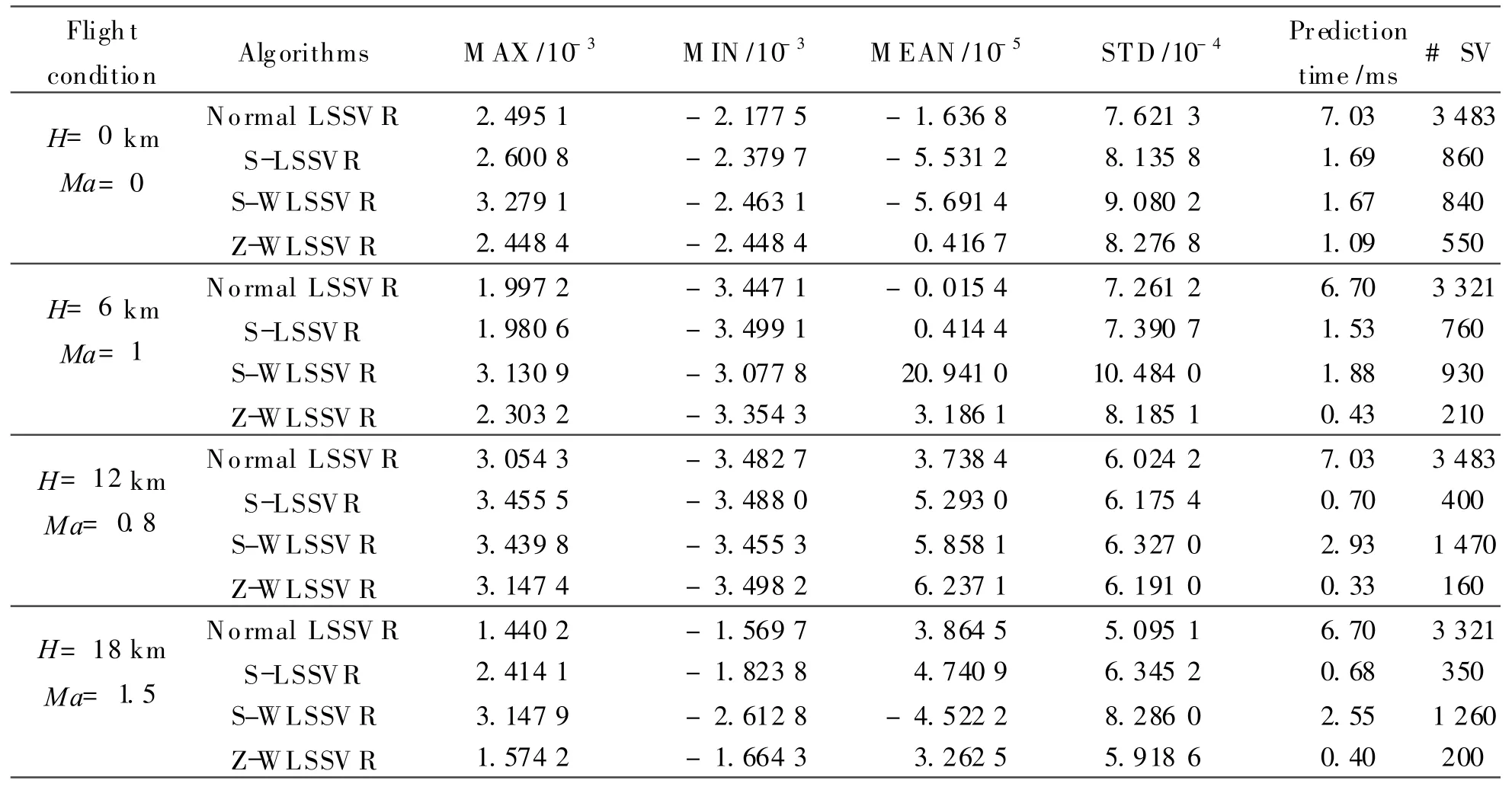
Table 1 Experimental results
3 CONCLUSION
Recently,the intelligent engine control has attracted much attention.As a representative,performance deterioration mitigating control is an advanced control concept for future aero-engines.The design of thrust estimator becomes the key issue for PDMC with high accuracy and excellent real-time performance under the condition of performancedegradation.The normal LSSVRis utilized to improve performance deterioration and SLSSVR is used to enhance the real-time performance.Considering the actual setting,a novel weighting strategy is proposed to improve the SWLSSVR′s drawback of reducing the real-time performance. By the aid of the proposed ZWLSSVR,the accuracy of thrust estimator satisfies the requirement of PDMC and its real-time performanceis enhanced further.Finally,the numerical experiments validate the proposed ZWLSSVR and its application.
[1] Litt JS,Simon D L,Garg S,et al.A survey of intelligent control and health management technologies for aircraf t propulsion systems[R].NASA/TM-2005-213622,2005.
[2] Garg S.NASA Glenn research in controls and diagnostics for intelligent aerospace propulsion systems[R].NASA/TM-2005-214036,2005.
[3] Litt JS,Frederick D K,Guo T.Thecase for intelligent propulsion control for fast engine response[R].AIAA 2009-1876,2009.
[4] Simon D L,Garg S. A systematic approach for model-based aircraft engine performance estimation[R].NASA/TM-2010-216077,2010.
[5] Adibhatla S,Brown H,Gastineau Z.Intelligent engine control(IEC)[R].AIAA 92-3484,1992.
[6] Gastineau ZD,Happawana G,Nwokah O D I.Robust model-based control for jet engines[R].AIAA-98-3752,1998.
[7] Guo T.A roadmap for aircraf t engine life extending control[C]//Proceedings of the 2001 American Control Conference. Piscataway:IEEE,2001: 3702-3705.
[8] Litt J S,Turso JA,Shah N.A demonstration of a retrofit architecture for intelligent control and diagnostics of a turbofan engine[R].AIAA-2005-6905,2005.
[9] Litt J S,Sowers T S.Evaluation of an outer loop retrofit architecture for intelligent turbofan engine thrust control[R].AIAA 2006-5106,2006.
[10]Garg S.Introduction to advanced engine control concepts[R].20070010763,2007.
[11]Litt JS. An optimal orthogonal decomposition method for Kalman filter-based turbofan engine thrust estimaton[R]. NASA/TM-2005-213864,2005.
[12]Zhao Y,Sun J.Boosting sparse least squares support vector regression(BSLSSV R)and its application to thrust estimation[J].Transactions of Nanjing University of Aeronautics and Astronautics,2008,25(4):254-261.
[13]Zhao Y,Sun J.Aeroengine thrust estimation using least squares support vector regression machine[J].Journal of Aerospace Power,2009,24(6):1420-1425.(in Chinese)
[14]Zhao Y,Sun J,Wang Q,et al.Thrust estimator design based on K-means clustering and reduced least squares support vector regression[J].Journal of Aerospace Power,2010,25(5):1177-1183.(in Chinese)
[15]Vapnik V N.The nature of statistical theory[M].New York:Springer-Verlag,1995.
[16]Cortes C,Vapnik V N.Support vector networks[J].Machine Learning,1995,20(3):273-297.
[17]Suykens J A K,Vandewalle J.Least squares support vector machine classifiers[J].Neural Processing Letter,1999,9(3):293-300.
[18]Suykens J A K,Brabanter J D,Lukas L,et al.Weighted least squares support vector machines:robustness and sparse approximation[J].Neurocomputing,2002,48(1/4):85-105.
[19]Suykens J A K,Lukas L,Vandewalle J.Sparseapproximation using least squarevector machines[C]//IEEE 2000 International Symposium on Circuits and Systems.Piscataway:IEEE,2000:757-760.
[20]Valyon J,Horváth G.A robust LS-SVM regression[J].Transactions on Engineering,Computing and Technology,2005,7(8):148-153.
[21]Zhao Y,Sun J.A non-flat function robust regression algorithm using multi-kernel LS-SVM[J].In-formation and Control,2008,37(2):160-165.(in Chinese)
[22]An S,Liu W,Venkatesh S.Fast cross-validation algorithms for least squares support vector machine and kernel ridge regression[J].Pattern Recognition,2007,40(8):2154-2162.
 Transactions of Nanjing University of Aeronautics and Astronautics2012年1期
Transactions of Nanjing University of Aeronautics and Astronautics2012年1期
- Transactions of Nanjing University of Aeronautics and Astronautics的其它文章
- PARAMETER OPTIMIZATION OF ELECTRIC POWER STEERING INTEGRATED WITH ACTIVE FRONT STEERING FUNCTION
- ADVANCED FREQUENCY-DIRECTED RUN-LENTH BASED CODING SCHEME ON TEST DATA COMPRESSION FOR SYSTEM-ON-CHIP
- DUAL QUATERNION CURVE INTERPOLATION ALGORITHM FOR FORMATION SATELLITES
- PROCESSING PARAMETER OPTIMIZATION OF FDM BASED ON ROBUST DESIGN
- PROPERTY AND THERMOSTABLITY STUDY ON TC6 TITANIUM ALLOY NANOSTRUCTURE PROCESSED BY LSP
- EXPERIMENTAL STUDY OF HTC FOR FILM COOLING OF PARALLEL-INLET HOLES
