简化核函数FFT运算复杂度和动态性能的优化
毕廷锋,周 涛,李 涛
(电子信息控制重点实验室,成都610036)
1 引 言
电子战中的数字侦察接收机需要较大的瞬时带宽和很高的接收灵敏度,这势必带来大量数据需要实时处理,而目前的数字硬件处理速度有限,如何对接收机前端带来的高速率采样数据进行快速处理是目前电子战接收机发展中的瓶颈,也是亟待解决的问题。
并行处理通过增加资源面积来换取处理速度的提升,可以做到数据的实时流水,然而其资源开销较大,对流水处理的控制时序要求也比较高。实时处理的另一种思路是通过改进或优化处理算法本身来提升处理速度,简化核函数的FFT[1]就是一种针对FFT接收机的有效处理算法,其乘法操作不需要复杂的浮点计算,而是用定点数移位和加减来代替,因此能够大大提高接收机的处理速度,处理时间显著减少,文献[2]中也指出这种处理方法在宽带数字接收机的快速处理领域具有很强的应用价值。文献[3]具体介绍了核函数的简化原理。文献[4]把4点和12点的简化核函数应用到了宽带数字接收机的核心FFT算法里,大大降低了算法的硬件资源消耗。文献[5]中提出对FFT的每一级采用不同的核函数简化方式,其单音信号的动态性能改善达到45 dB,但算法实现比较复杂,简化点数甚至到128点。文献[6]对简化核函数的DFT滤波信道的动态性能进行了详细分析,指出简化核函数的FFT信道性能要比DFT信道要差,但没有具体分析简化核FFT的动态性能。
上述文献都没有对简化核FFT的计算复杂度和动态性能进行比较全面的分析。基于此,本文首先阐述了FFT核函数的简化原理和6种简化模型,指出简化核函数FFT在提高运算速度的同时,会降低接收机的瞬时动态范围(IDR),这就有必要优化其处理时间和动态性能。由于6种简化模型的处理时间和动态之间并不是线性的反比关系,这为两者的优化提供了可能。本文接下来基于Cooley-Tukey算法,分析6种核函数简化点数的FFT运算量;然后对接收机带宽内步进单频信号的瞬间动态做了统计分析,用其平均值和稳定性来评价6种简化点数的动态性能;最后经过综合比较,得到运算时间较少、动态性能较优的核函数简化方式。
2 简化核函数FFT算法
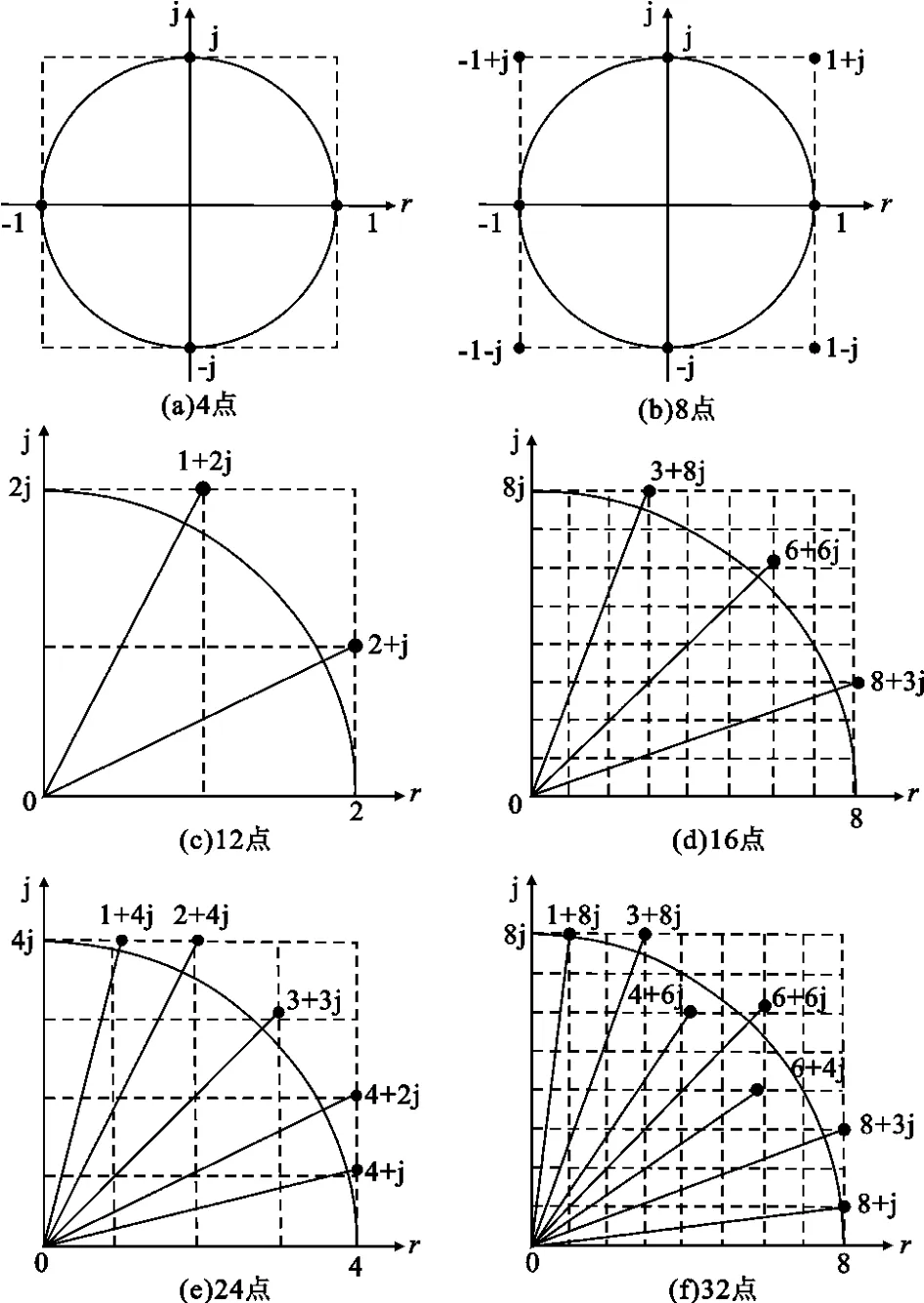
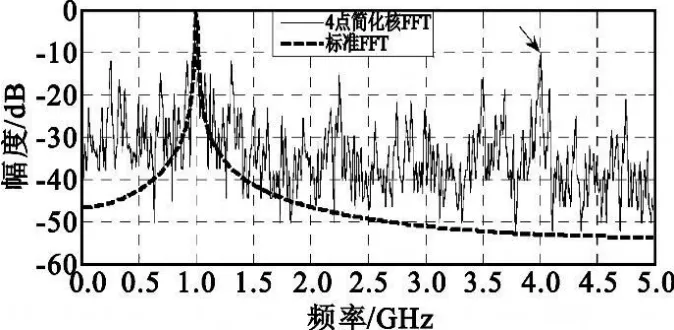
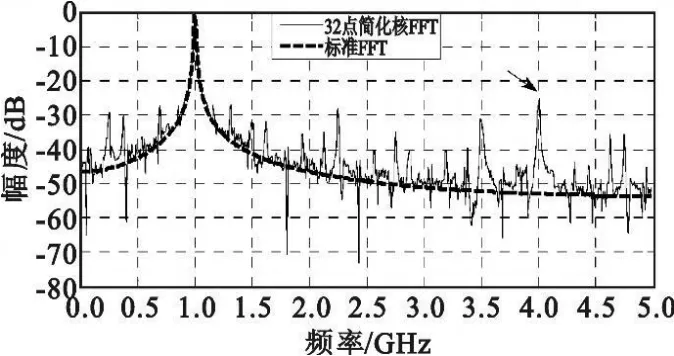
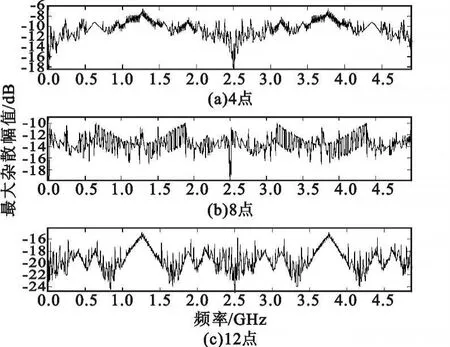
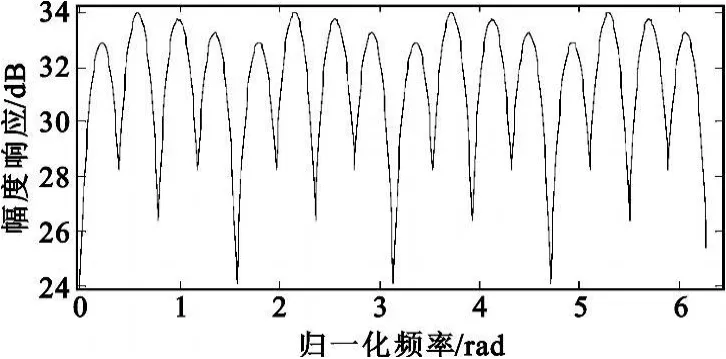
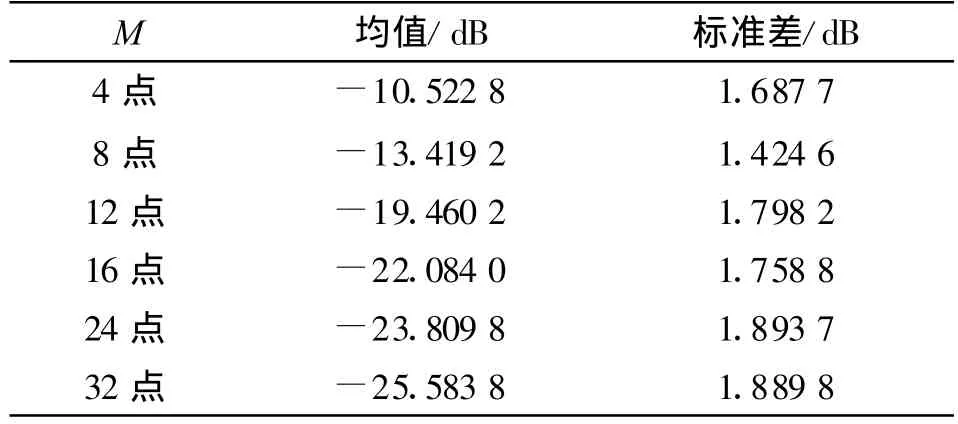
FFT的旋转因子ejφ是个浮点值,而且有N种选择,在实现中涉及到复数的浮点乘法计算,运算量比较大。如果能进一步将旋转因子缩减为有限个值(< 式(1)表示旋转因子 ejφ的 4点简化函数G(ejφ),可见,4 点简化 G(ejφ)和 ejφ的误差是比较大的。简化误差 G(ejφ)-ejφ是产生频谱杂散的原因,随着简化点数的增加,G(ejφ)越接近ejφ,杂散就会减少。 本质上,旋转因子的简化是把单位圆上N个旋转因子作了矢量量化和近似,变为 N个定点数矢量 。图1 是 4、8、12、16、24 、32 点简化原理的示意 ,黑点表示旋转因子简化后的取值。 图 1 旋转因子的 4、8、12、16、24、32点简化示意Fig.1 Simplified kernel function of 4,8,12,16,24,32 points 增加简化点数时,为了使定点矢量更好地近似到量化后的浮点矢量附近,可以把单位圆放大 R倍。便于硬件计算,一般取R为2的幂次。图1的12、16、24、32点简化表示了第一象限的取值,其他象限和第一象限对称,R分别取值2、8、4、8。 由于旋转因子的量化是一个非线性过程,其次用定点数近似浮点数,频谱分析结果和标准FFT会存在误差,产生频谱杂散,因此,简化核FFT在提高运算速度的同时,会降低接收机的瞬时动态范围。由于6种简化方式所取的定点数不同,对浮点数的近似程度不一样,使得处理时间和IDR性能并不是线性的反比关系。在上述的6种简化模型中,并不是简化点数越少,IDR性能越差。因此,在其中寻找兼顾计算时间和动态性能的简化方式是可能的。 不同FFT结构的蝶形数目不一样,它们的计算量也有差别。另外,简化点数越多,FFT计算量越大。基于快速处理性能的考虑,本文讨论的简化核FFT采用Cooley-Tukey算法,并用较少的简化点数:4、8、12、16、24、32 点。 N点Cooley-Tukey FFT的第 v级旋转因子为它们的取值落在第三象限和第四象限,经过M点简化,第三象限和第四象限共有M/2个旋转因子简化值。因此,在N点FFT计算流程中,每个简化值约用到N/(M/2)次,即每个简化值要参与2N/M次复乘运算。 显然,简化核FFT保留了标准FFT原有的加法次数,增加的是用来取代乘法运算的移位数和加法数。蝶形输入对6种简化旋转因子的乘法只涉及到对定点数 1、2 、3、4、6、8 的乘法。具体来讲,蝶形输入乘以 1、2、4、8,只需对输入分别做 0、1、2、3 次二进制移位;而3可以表示为 21+1,6表示为22+21,因此蝶形输入乘以3和6,需要对输入分别移位1次和2次,还要分别做1次加法。 另外,如果旋转因子的矢量半径放大到R,为了恢复原先采用单位圆旋转因子时的计算结果,应在蝶形乘法之后除以R。由于6种简化方式中R均是2的幂次,该除法用移位即可实现。 基于3.1节的分析,假定 x表示简化后的旋转因子取值,mx和nx分别表示蝶形输入与x相乘时需要进行移位和加法的次数,sM表示蝶形计算结果除以放大倍数R需要的移位次数,6种简化方式的sM值依次是 0、0、2、6、4、6。这样,可以得到 M 点简化核FFT的复移位数和复加数的计算公式如下: 其中,式(2)的 NlbN/2是蝶形个数,式(3)的 NlbN是原有的复加数。表1是6种简化点数所需的移位和加减操作数,都能在硬件实现的一个时钟周期内完成,因此从总耗时来看,计算一次完整的M点简化核FFT,16点和32点简化的运算时间最多,其次是24点,接下来是12点,时间最少的是4点和8点,只对蝶形输入做加法。 表1 M点简化核FFT的运算量Table 1The computation complexity of M-point simplified kernel function FFT FFT作为DFT的快速算法,并没有严格的解析表达式,外加FFT核函数的量化是非线性过程,因此很难用解析方式推导简化核FFT的运算结果。本文通过仿真来分析不同简化点数Cooley-Turkey FFT的动态性能。 FFT旋转因子的非线性简化过程会产生信号峰值外的很多杂散分量,尤其在简化点数较少时,这会影响到接收机的动态性能。 假设采样率为10 GHz,信号积累时间N=1 024点。若把主瓣附近几个频域分量除去,余下的分量看作杂散,则图2和图3是1GHz点频信号做4点和32点简化FFT的频谱,分别和标准FFT做了比较,箭头指出了简化核函数后的最大杂散值。 图2 4点简化FFT的频谱Fig.2 The frequency spectrum of 4-point simplified kernel function FFT 图3 32点简化FFT的频谱Fig.3 The frequency spectrum of 32-point simplified kernel function FFT 可见,1 GHz点频时,4点简化的杂散峰值约-10 dB,事实上带宽内其他点频产生的杂散峰值甚至更大。而简化点数越多,结果越接近标准FFT,杂散效应减弱,32点简化的杂散明显减少,最大杂散值约-26 dB。 第2节指出,简化FFT的杂散是由简化函数的误差 G(ejφ)-ejφ引起 ,而 G(ejφ)矢量在 4 个象限的取值是对称的,因此误差 G(ejφ)-ejφ也呈象限对称。另外,从傅里叶变换相关角度来讲,输入信号与核函数ejφ的相关在圆周的某一点取得最大值,那么该点核函数表示的频率就是信号的频率。因此在全频段内,G(ejφ)-ejφ呈象限对称,杂散谱也应该是呈象限对称的。 对此,在 0~5 GHz带宽内设置1 000个步进点频,步进频率为5 MHz,考察杂散峰值随着频率的变化情况,有图4和图5所示的变化规律。 图4 4点、8点、12点的杂散峰值分布规律Fig.4 The peak spur′s distribution of simplified kernel function FFT with 4,8,12 points 图5 16点、24点、32点的杂散峰值分布规律Fig.5 The peak spur′s distribution of simplified kernel function FFT with 16,24,32 points 可见,杂散峰值的频域分布呈周期重复,共有4个变化周期,整个带宽内依次呈镜像对称,对应于圆周上的象限对称,符合理论分析。因此前1/4频段0~1.25 GHz的杂散情况代表了其他3个频段。而0~1.25 GHz内不同频点的杂散峰值在一定范围内波动,原因分析为:离散傅里叶变换可以看作是一组均匀的梳状滤波器组,一个点频信号可以通过某一滤波器,而在其他滤波信道没有输出。核函数简化后的滤波器组不是均匀状,有周期性起伏,如图6所示,这样相同功率的点频信号位于不同滤波信道内,其杂散峰值就有波动。 图6 简化核FFT的滤波信道Fig.6 The filtering channel of simplified kernel function FFT 因此,取前1/4频段0~1.25G内250个频点的杂散峰值做统计分析,其平均值和波动性如表2所示。 表2 杂散峰值分布规律的统计结果Table 2 The statistical results of peak spur′s distribution 表2结果中可得: (1)从瞬时动态的平均值来看,4点简化的最小,约-10 dB,12点简化的动态达到约-20 dB,32点达到-26 dB,因此,4点到12点、12点到32点的提升幅度比较明显,分别改善了10 dB和5 dB; (2)用标准差衡量动态性能的稳定程度,则8点简化的稳定性最好,其他简化方式的波动较大; (3)综合平均值和稳定性来看,12点以上的动态性能随着输入频率的波动性较强,8点的动态性能比较稳定,但动态范围比12点小6 dB,而12点的动态范围达到约-20 dB,但没有8点稳定。 综合比较6种简化点数的运算时间和瞬时动态性能:32点简化的动态约-26 dB,是6种简化方式中平均动态最好的,但其运算量较大;而8点和12点的运算量较少,两者之中,8点的动态性能比较稳定,平均值比12点小6 dB;12点的动态较大,但频域分布的波动性也强。从计算复杂度来看,8点简化的FFT运算没有移位操作,仅需要进行NlbN次复加,12点运算还需要移位NlbN次,积累时间 N较小时,两者的运算量差别不大,当积累时间较长时,8点简化FFT的运算优势明显。 简化核函数FFT用移位和加法操作取代了乘法计算,显著地减少了处理时间。简化点数越少,计算时间越快,但是旋转因子的简化会产生频谱杂散,特别是在简化点数较少的情况下,影响到FFT的动态性能。由于各种简化点数所取的定点数不同,对浮点数的近似程度不一样,导致处理时间和IDR性能并不是线性的反比关系,这为两者之间的优化提供了可能。本文综合分析了6种简化点数下FFT的计算量和瞬时动态性能,通过比较分析,得到在两者间优化的相关结论,对宽带数字接收机的性能优化有工程参考价值,并可以应用到电子侦察等快速信号处理领域。 [1]Tsui J.宽带数字接收机[M].杨小牛,译.北京:电子工业出版社,2002.Tsui J.Wideband digital receiver[M].Translated by YANG Xiao-niu.Beijing:Publishing House of Electronic Industry,2002.(in Chinese) [2]周涛.电子战中的单比特数字化接收技术[J].电子对抗,2006(5):6-10.ZHOU Tao.Technique of Monobit Digital Receiver in Electronic Warfare[J].Electronic Warfare,2006(5):6-10.(in Chinese) [3]Schamus,et al.Quad-bit Kernel Function Algorithm and Receiver:US,6 690 315 B1[P].2004. [4]Chen C H,George K,McCormick W,et al.Design and Performance Evaluationof a 2.5-Gsps Digital Receiver[J].IEEE Transactions on Instrumentation and Measurement,2005,54(3):1089-1099. [5]Sarathy V.High Spurious-Free Dynamic Range Digital WidebandReceiver for Multiple Signal Detection and Tracking[D].Dayton,Ohio:Wright State University,2007:35-45. [6]Grajal J,Lopez-Risueno R B G,Sanz J M.Analysis and Characterization of a Mono-bit Receiver for Electronic Warfare[J].IEEE Transactions on Aerospace and Electronic Systems,2003,39(1):244-258.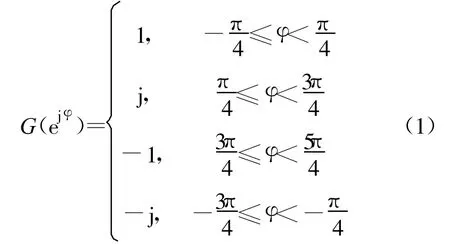
3 运算复杂度分析
3.1 旋转因子简化后的蝶形乘法
3.2 6种简化核FFT的运算量
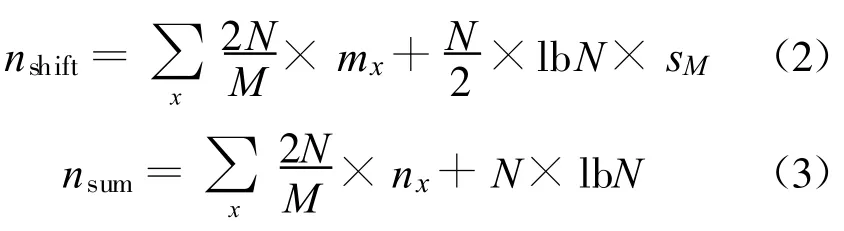

4 动态性能分析
4.1 简化核函数的杂散效应
4.2 杂散的分布规律

4.3 运算复杂度和动态性能的优化
5 结束语

