伪逆矩阵的一种改进解法及其在自由网平差和拟稳平差中的应用

范国庆，杨喜平

(武汉大学测绘学院，湖北武汉430079)

伪逆矩阵的一种改进解法及其在自由网平差和拟稳平差中的应用

范国庆，杨喜平

(武汉大学测绘学院，湖北武汉430079)

提出伪逆阵的一种改进解法，该方法不但理论严密、计算简单，而且解伪逆阵的公式易于编程实现，可以同时用在自由网平差和拟稳平差中，它还可以将这两种平差结合起来对变形监测网基准点进行稳定性检验和分析，最后通过实际算例验证该方法的有效性。

伪逆阵;基准点;自由网平差;稳定性分析;拟稳平差

一、引 言

自由网平差和拟稳平差的数学模型是相同的，差别在于采用不同的参考系。在平差过程中，如果没有足够的起始数据，就会引起误差矩阵的系数阵列亏，这就是秩亏自由网平差。为了解决该问题，参考文献［1］已阐述了较多的方法。在秩亏自由网平差中，需要对伪逆矩阵求逆，传统的解法计算繁琐、工作量大。本文根据伪逆矩阵对其解法进行改进，得到了一种解伪逆阵较简单的公式，此公式计算简单、易于在编程过程中实现，并且可以简单地将自由网平差、拟稳平差和网点稳定性检验联合在一起，直接计算网点的位移量。

二、伪逆阵解法的改进及其在秩亏自由网平差和拟稳平差的应用

1.秩亏自由网平差的基本原理

秩亏自由网平差的函数模型为［2-4］。

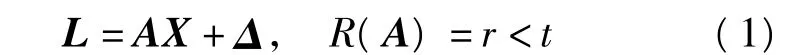
式中，A的列亏数d=t－r，随机模型为

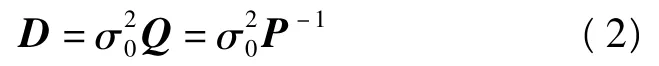
式(1)的误差方程为

平差原理为

法方程为

式中，N=ATPA。

由于R(N)=R(A)=r，所以N奇异，为消除秩亏可以附加如下的约束条件

式中，R(G)=d。式(5)要满足的条件有：①网的条件数量等于秩亏数;②GT矩阵的行跟A矩阵的行需要独立线性。

结合式(4)和式(5)得到［5］

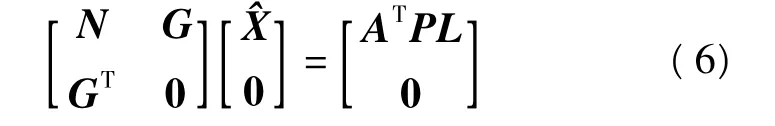
式(6)的系数矩阵的逆矩阵可以用块矩阵表示

式中，N－为N的一种伪逆阵形式。

因此，未知参数求解为

单位权方差估值仍为

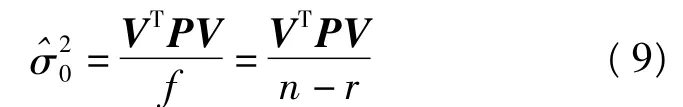
2.解伪逆阵的一种改进解法

由式(7)得出下面的等式

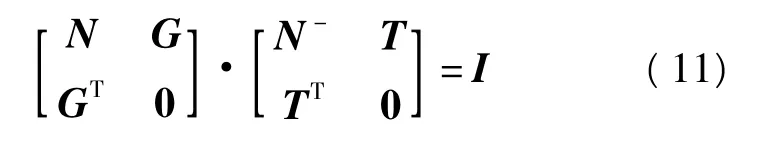
式中，I为单位阵，由式(11)可得

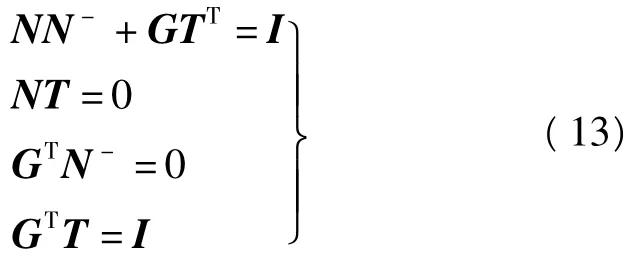
由式(12)有

(1)计算T矩阵

由式(14)可得

将式(15)的两边乘以Bt，d得

若B矩阵满足性质

则N－NB=0，求得T矩阵为

因自由网平差和拟稳平差的参考系方程系数矩阵(或称基准转换矩阵)满足式(17)，所以在平差过程中，选B矩阵为参考系方程系数矩阵。

(2)计算N－矩阵

由式(13)可知

式中，P0为d×d阶的矩阵，不变。

由GTN－=0，则

所以

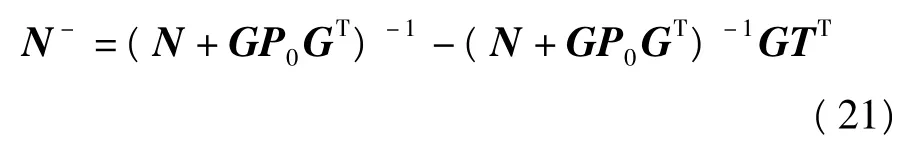
另外，由NT=0和GTT=I可知，G阵相当于

最后得到

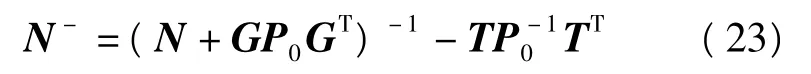
当P0=I时

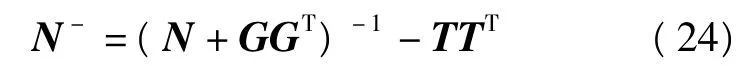
特殊的情况下，当G=B时，N－矩阵就满足广义逆N+矩阵，即

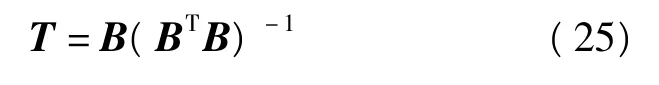
则有

实际计算中，式(23)中的P0矩阵常选为对角矩阵

有

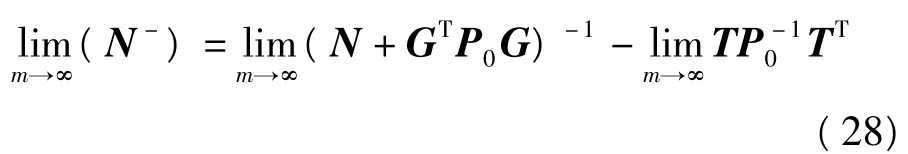
实践证明［5］，当m≥6时，式(29)即满足精度要求。

三、伪逆阵改进公式的应用

1.在自由网平差和拟稳平差中的应用

在自由网平差中，为了简单运用式(29)，对高程网来说，常选

对平面测角网来说，有

式中，i=1，2，…，n，为网点数;(Xi，Yi)相应为点的近似坐标。若是平面测边网或平面测边角网，则式(31)的矩阵没有4列。

对于拟稳平差，G阵的形式跟自由网平差一致，差别在于，哪个网点是动点，G阵相应的值就为零，若点i是动点，则Gi=Bi=0。

2.联合自由网平差和拟稳平差对网点稳定性检验

从理论上可知，自由网平差和拟稳平差的差别在于参考系方程系数矩阵B的选择问题。在变形监测数据处理中，如果采用自由网平差，除了第1期外，每周期都要进行基准网点稳定性检验，现代测量数据处理理论具有很多方法可以发现基准网点是否稳定，如平均间隙法、稳健迭代权法、单点位移分量法等，具体的理论可以参考文献［1，6］。本文利用上述公式，联合自由网平差和拟稳平差对网点进行稳定性检验，网点稳定性检验采用平均间隙法，此方法的思想是：首先对两期观测值进行自由网平差(同近似坐标)，G矩阵的选择如式(30)或式(31)，利用平均间隙法对网点稳定性进行检验之后，如果网中存在动点，将网的动点再选G矩阵，即

由于执行基准点稳定性检验及式(32)不可能同时计算，那么最好的解法应该是使用重复的方法计算，直到网中没有动点为止。该方法的实现步骤如下：

1)对第i－1期基准网进行自由网平差，首先通过间接平差得到网中各点的坐标，然后把得到的坐标作为自由网平差的近似坐标。

2)在第i期，假定所有网点都是稳定点并选矩阵Gi=Bi进行自由网平差;两期的近似坐标一致。

3)利用平均间隙法进行基准点稳定性检验，首先对网进行整体检验，看网中是否存在动点。若发现网中具有动点，则用“尝试法”［6］将不稳定点找出来，找到动点就按照式(32)改变G矩阵，然后用新的G矩阵进行自由网平差，继续对网点检验，直到没有动点再进行下一步。

4)对网中不稳定的点运用第3)步中的G矩阵继续进行平差处理，获得的最后结果与拟稳平差的结果一致。

上述步骤的流程如图1所示。

图1 自由网平差和拟稳平差联合的流程图

四、算例分析

以某大坝的变形监测基准网为例，网中具有8个点，如图2所示，该网是加密网，其中1、3、5、7点是已知点。选择第1期和第2期的观测数据进行试验分析，该网每期测25个角和12条边长，观测数据记在表1和表2。利用VB6.0语言根据上述的步骤编制了一个结合自由网平差、拟稳平差对网点稳定性检验的软件。

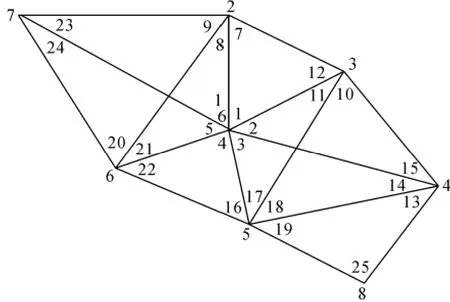
图2 某大坝变形监测基准网

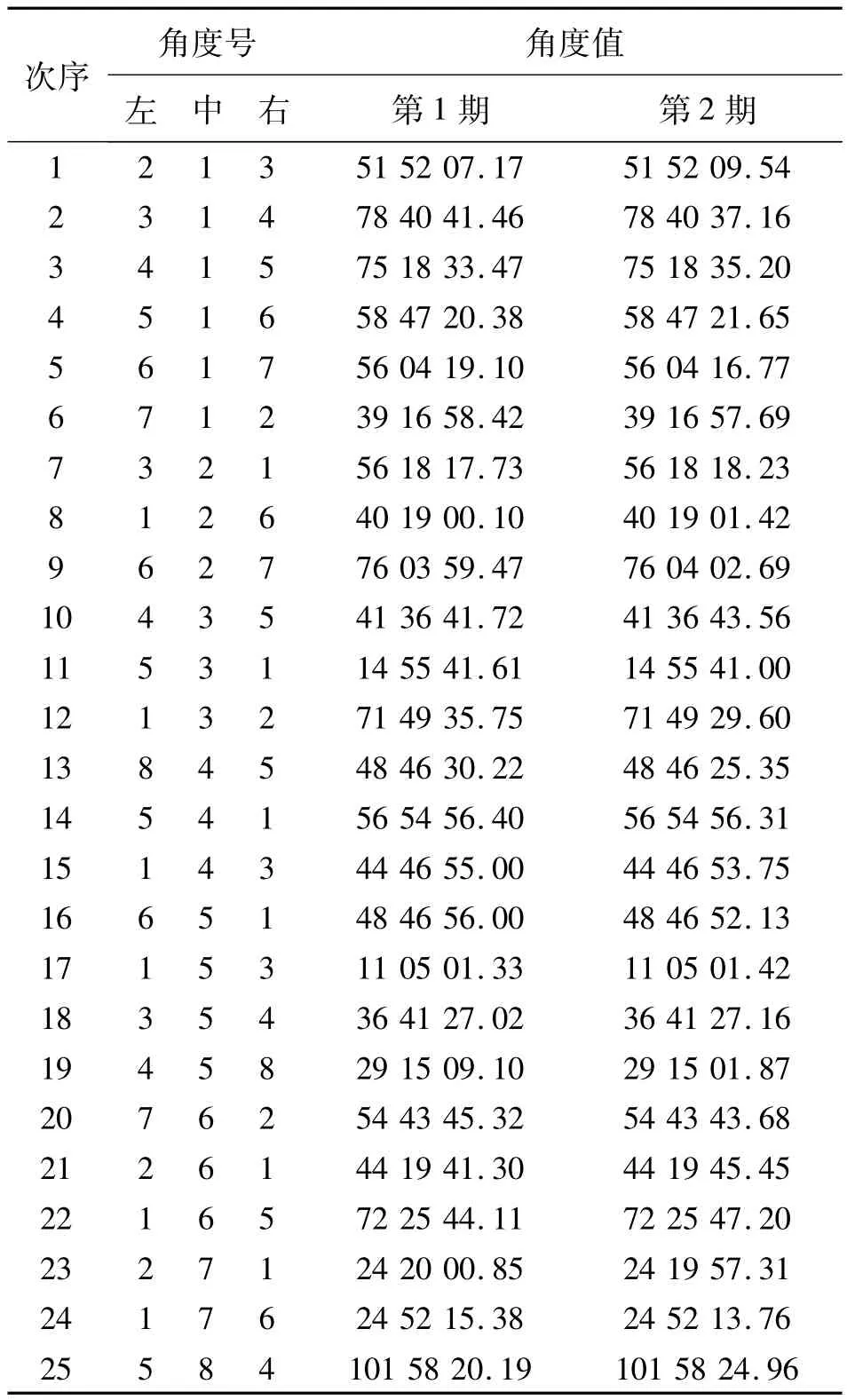
表1 两期角度观测值 (°'″)

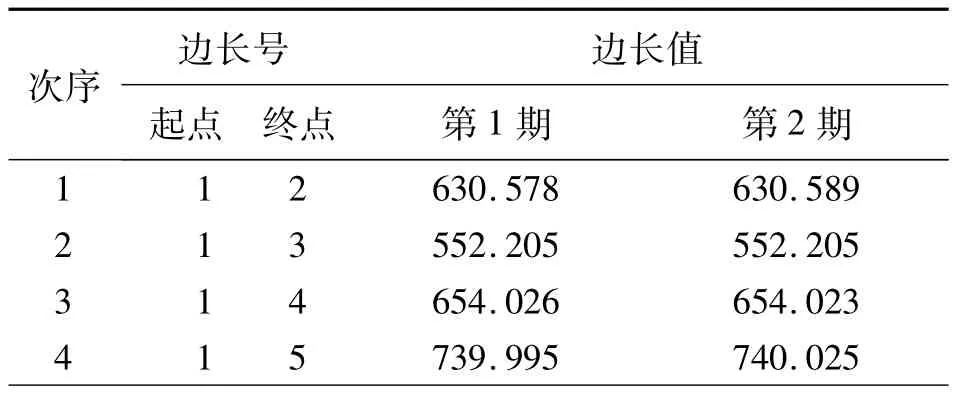
表2 两期边长观测值 m

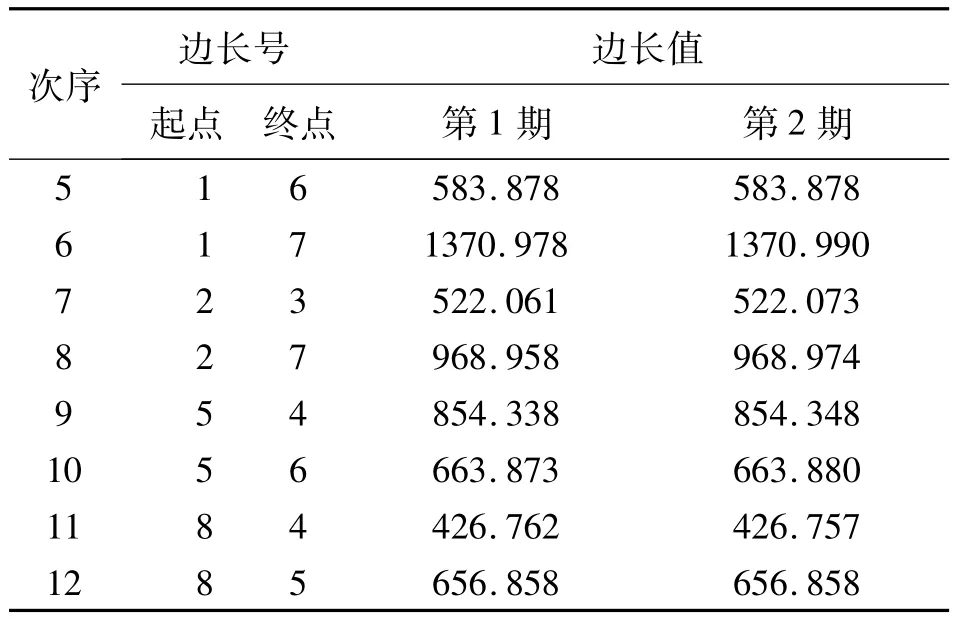
续表2 m

处理过程如下：

1)第1期的处理要凭4个已知点(1、3、5、7点)进行间接平差，其次把平差后的坐标作为第1期自由网的近似坐标(见表3)，然后对第1期观测的数据进行自由网平差。处理过程中，运用本文的式(29)得到第1期的平差坐标见表3。

表3 网点近似坐标和第1期平差坐标 m

2)第2期自由网计算的近似坐标和第1期一致，对于G矩阵，首先认为所有网点是稳定点，则G矩阵对应为

式中，i=1，2，…，8，为网点数;(Xi，Yi)为相应网点的近似坐标。进行自由网平差后得到网点平差坐标。将第2期和第1期平差后的坐标对比，获得网点的位移量见表4。

表4 网点的第2期的自由网平差坐标与网点的位移量

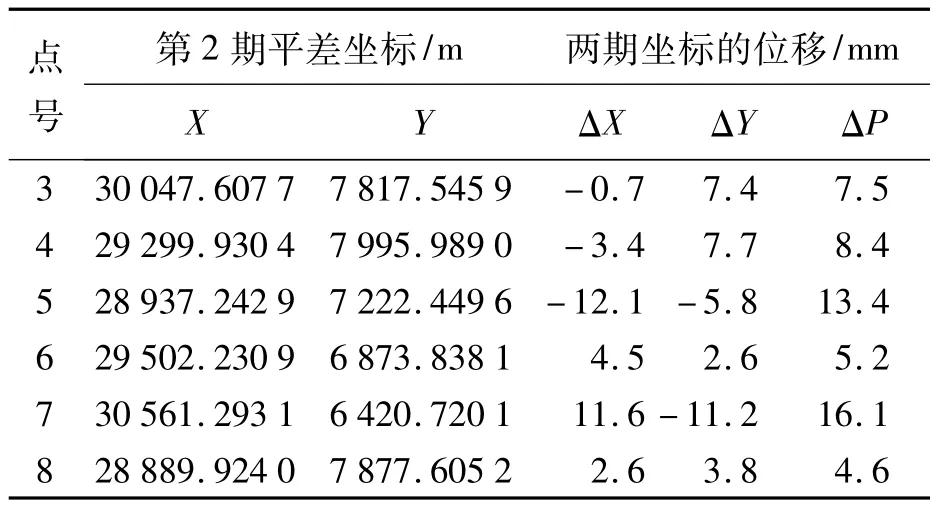
续表4

3)采用平均间隙法进行网整体检验是否有动点，得到统计量F=2.28。取显著水平α=0.05，则F0.05(24，24)=1.98，由于F＞F0.05(24，24)，因此认为两期观测期间网中存在动点。

用平均间隙法找不稳定点要用到“尝试法”，找到点7是动点，所以令

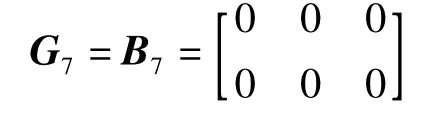
重新计算，再执行检验，发现点5也是动点，又令

继续计算和检验，获得统计量F=0.74＜F0.05(24，20)=2.08，所以接受原假设，认为余下的各点均为稳定点，检验过程到此为止。

4)将新的G矩阵代入进行自由网平差，这时自由网平差就变成拟稳平差，因此获得的结果等于拟稳平差的结果。两期之间的新平差坐标和新位移量见表5。

表5 网点的第2期的拟稳平差坐标与两期位移量

用拟稳平差原理进行平差获得的结果与上面的方法一致。

五、结 论

1)采用式(29)求解伪逆阵在自由网平差比较简单，只通过一个公式即能得到N+矩阵。

2)根据本文提出的流程不仅能使编程过程容易实现，而且还能把变形监测基准网数据处理中的自由网平差、基准网稳定性检验和拟稳平差联合起来进行处理，直接获得网点位移量。

3)变形监测基准网在处理过程中必须进行网点稳定性检验，因此这种方法用于变形监测基准网是比较有效的。

［1］ 陶本藻.自由网平差与变形分析［M］.北京：测绘出版社，2001.

［2］ 黄声享，尹晖，蒋征.变形监测数据处理［M］.武汉：武汉大学出版社，2003.

［3］ 侯建国，王腾军.变形监测理论与应用［M］.北京：测绘出版社，2008.

［4］ 朱建军，贺跃光，曾桌乔.变形监测的理论与方法［M］.长沙：中南大学出版社，2004.

［5］ TRAN K.自由网平差在工程测量数据处理中应用研究［D］.河内：越南河内矿业地质大学，1996.

［6］ 黄声享.监测网的稳定性分析［J］.测绘信息与工程，2001(3)：16-18.

An Improved Pseudo-inverse Matrix of the Solution and Its Application for Free Network Adjustment and Quasi-stable Adjustment

FAN Guoqing，YANG Xiping

0494-0911(2012)09-0011-05

P207

B

2012-01-04

范国庆(1978—)男，越南人，博士生，主要研究方向为变形监测数据处理、分析与预报。