个体机器人局部路径规划的人工力矩方法

徐 望 宝， 陈 雪 波， 赵 杰

(1.大连理工大学 电子信息与电气工程学部，辽宁 大连 116024；2.辽宁科技大学 电子与信息工程学院，辽宁 鞍山114051；3.哈尔滨工业大学 机器人技术与系统国家重点实验室，黑龙江 哈尔滨150001)

0 引 言

二维障碍平面中个体自主移动机器人的局部路径规划问题，是机器人学中的一个重要问题.其目的就是要求一个对环境无任何先验知识的机器人，仅依靠其传感器的实时探测和运动过程中积累的环境知识，规划出一条从起点位置到目标位置的无碰较优路径，或证明不存在这样的路径.

针对上述问题，目前人们已提出了较多的解决方法，其中比较重要的有“沿墙走”方法或“Bug”方法[1～3]、人工势场法[4～6]等.“Bug”方法的基本原理是:机器人总试图直接向着目标点运动；在遇到障碍时，才沿着障碍往前走直到确定已绕过了障碍.“Bug”方法有直观、简单、在一定条件下能保证收敛的优点；缺点是未曾考虑运动路径的长度，即路径优化问题.人工势场法的基本原理是:机器人活动在一个人工力场中，其中目标对机器人有一个吸引力，障碍对机器人有一个排斥力；在合力作用下，机器人沿使合力减小的方向运动.人工势场法有实时性强、计算简单、实现容易等优点；缺点除了未曾考虑路径优化问题外，还存在一个比较难以解决的“局部极小点”问题[2、6].

在满足约束的条件下，机器人的运动路径越短越好.所以在局部路径规划问题中，也应考虑路径优化问题，即利用现有的环境知识，得到一条尽可能短的运动路径.基于公路图的方法，如可视图方法[7]、切 线 图 方 法[8]、Voronoi图 方 法[9、10]等，是注重路径优化的方法.这类方法的基本原理是:首先，机器人要得到一个由可行路径组成的公路图，该图必包含机器人当前位置与目标间的最短可行路径；然后，运用某种技术如Dijkstra算法或图理论[9]，机器人从该公路图中选出最短可行路径并沿该路径运动.这类方法的主要优点是常能得到最优可行路径；缺点是在局部路径规划问题中，由于环境知识不断改变，需要经常重新计算公路图及最短可行路径，计算量很大，难以在局部路径规划问题中使用.

本文首先将公路图方法中的有关概念进行推广，提出广义可行路径和最优路径代表点(Powr)等概念.最优路径代表点，除在优化路径时，有与最短广义可行路径相同的效果外，还有存储量小，不需要像公路图方法一样考虑机器人的半径与安全距离[8]，也不需要对环境做预处理等优点.然后将文献[11、12]提出的用于多机器人队形控制的人工力矩方法进行推广，设计在通常情况下会努力使机器人基本运动方向线(PMDline)指向Powr的新吸引矩函数和总努力使机器人的PMDline背向相应危墙代表点的新排斥矩函数.基于上述两种人工力矩，设计机器人运动控制器.当机器人与目标间的线段被障碍阻断时，该控制器会使机器人沿PMDline以最大步幅运动，从而即使面临复杂的障碍，机器人也不会停止运动，即不会被陷住.所以基于人工力矩规划机器人路径不会产生类似“局部极小点”的问题.

本文还给出最优路径代表点的求解方法、个体机器人局部路径规划的基本步骤及可达性证明.

1 系统模型与相关定义

本文仅讨论二维平面中个体机器人的局部路径规划问题，其中工作环境中分布有静态的多边形障碍；机器人对环境无任何先验知识，要求仅依靠传感器的实时探测和运动过程中积累的环境知识来规划一条能安全到达目标的路径；到达目标后，机器人还要尽可能地具有给定的位姿.

在讨论问题的解决方法前，首先规定文中使用的一些符号和概念，其中一有向线(射线或有向线段)到另一有向线的角，及有向线方向角的定义与文献[11]相同，即将一有向线绕其端点旋转到与全局坐标系中横坐标轴方向相同时所转的绝对值不大于π的有向角就是该有向线的方向角.设βi、βj分别是有向线li、lj的方向角，函数

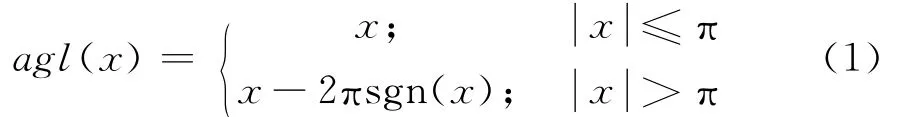
那么β＝agl(βi－βj)就是从li到lj的角.

定义Time＝｛tk｜k＝0，1，…｝为一离散时间点集.任意变量X在tk时刻的值用X(k)表示；如果一变量值的时间没有指定，则为当前时刻；如果X是一条连续曲线段，则｜X｜是它的长度.AB表示以A、B为端点的线段；Sd(A，B)表示以A为起点、B为终点的有向线段，β(A，B)为Sd(A，B)的方向角；Lr(A，B)表示以A为起点、经过B的射线. (W，－A1，…，－An)表示连续曲线W上除A1，…，An外的点； (Lr(A1，A2)，－A1A2)表示Lr(A1，A2)上除A1A2外的所有点.

R表示机器人；SR表示R的最大运动步幅；Ds是一个与机器人的安全相关的正常数.R的模型如图1所示，其形状是一个半径为DR(Ds＞2SR＋2DR)的圆.R的位置(圆心位置)记为PR，坐标记为(xR，yR).像文献[11、12]中的机器人模型一样，R有且只有一条以其所在位置为端点的基本运动方向线(PMDline).该PMDline是一条以PR为端点、βR为方向角的射线，主要用来指示R的位姿或主要运动方向.

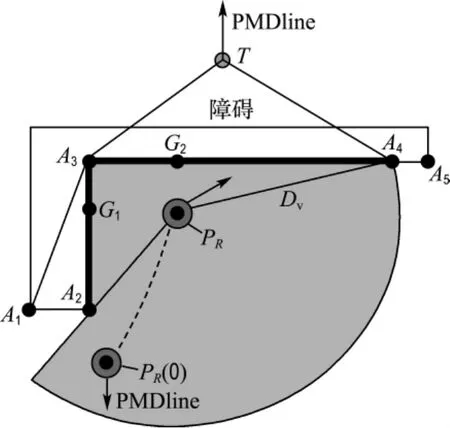
图1 相关模型Fig.1 Associated models

R有一个全方位传感器，其有效半径为Dv.对于工作空间中的点F，只有当且PRF不经过任何障碍时，R才能探测到F，否则探测不到F.如在图1中，R在当前时刻只能探测到灰色区域内及其边界上的点，该区域外的点如A1(A1在初始时刻能被R探测到)、A5就不能被探测到.

目标记为T，其模型为一个静态的质点，如图1所示，坐标记为(xT，yT).T有且只有一条以其位置为端点、βT为方向角的PMDline，用来指示其位姿.文中要求R到达目标后尽可能地具有给定的位姿，即要求R到达目标后，尽可能地小.

假设1 在任意时刻，R通过通信等方式，总能知道T的位置及PMDline的方向角.

假设2 任意两障碍间的最近距离都不小于Ds；R与T间至少存在一条宽度不小于Ds的路径.

定义1 设Σ是障碍物边缘线上一段连续的曲线.如果Σ上不含从未被R探测过的点，且对于任意的与Σ在同一个障碍物边缘曲线上的曲线段Σ＊，Σ＊Σ就意味着Σ＊上至少有一点从未被R探测到，那么称Σ为知识障碍墙.

如在图1中，折线段A1A2A3A4就是一条知识障碍墙；而折线段A1A2A3A4A5不是，因为上面有些点，如A5，从来没有被R探测到.

显然，知识障碍墙是环境知识积累的结果.R会记下所有的知识障碍墙并及时更新，以方便应用.

定义2 设W是一条以F1、F2为端点的连续曲线，S是所有以F1、F2为端点，上面的点或在W上或无限地靠近W的连续曲线组成的集合.①如果S中存在一个元素W＊，使得集合 (W＊，－F1，－F2)中不含任何知识障碍墙上的点，那么W就是一条以F1、F2为端点的广义可行路径.②如果存在一条知识障碍墙Σ，使得S中的每一个元素，都至少与Σ有一个公共点，那么就说W被Σ阻断.③如果一条射线上面的任何一条线段都没有被Σ阻断，那么该射线没有被Σ阻断，否则它就被Σ阻断.

如在图1中，折线段PRA4T和PRA2A1A3T都是以PR、T为端点的广义可行路径；而折线段PRA2A3T就不是，因为它被知识障碍墙A1A2A3A4阻断.

广义可行路径与完全可行路径密切相关，因为在一条广义可行路径的附近一定存在一条完全可行路径.但由于广义可行路径上可能存在障碍点，R的模型具有几何形状且R在运动过程中要与障碍保持一定的安全距离，所以广义可行路径又不一定完全可行.

定义3 设F是T或知识障碍墙上的一个点，如果PRF位于以PR、T为端点的最短广义可行路径上，且F≠T就意味着对任意的满足A∈ (Lr(PR，F)，－PRF)且｜FA｜＜Ds的点A，集合 (FA，－F)中都不含知识障碍墙的点，那么称F为最优路径代表点，记为Powr.

例如，当PRT不被任何知识障碍墙阻断时，PRT就是以PR、T为端点的最短广义可行路径，此时T就是Powr.

概念“最优路径代表点”含有两层意思:一是指Powr能够代表以PR、T为端点的最短／最优广义可行路径，因为直接向着Powr运动就会沿着该路径运动；二是指在所有能代表该路径的点中，Powr几乎是最优的，因为它几乎是所有既位于该路径上，同时与PR的连线段又不被任何知识障碍墙阻断的点中，距PR最远的点.

对于路径优化，Powr与以PR、T为端点的最短广义可行路径的作用完全相同；但显然Powr需要的存储量要少得多.同时Powr也不需要像完全可行路径那样考虑机器人的大小和安全距离，也不需要预处理环境，计算容易，所以在本文中，R主要是在Powr的引导下向着T运动.

定义4 设G是知识障碍墙Σ上能被R探测且到PR的距离不大于Ds的点，如果存在一个正常数δ，使得对任意的满足在Σ上且｜AG｜＜δ的点A，都有｜PRA｜＞｜PRG｜，那么称G为危墙代表点.

显然，危墙代表点就是对R具有安全威胁的知识障碍墙上的局部最近点.由于仅是局部最近点，同一知识障碍墙上的危墙代表点可能不只一个，如在图1中的当前时刻，在知识障碍墙 ——折线段A1A2A3A4上就有两个危墙代表点G1、G2.危墙代表点的主要作用是防止R向其所在的区域靠近，所以同一知识障碍墙上有多个危墙代表点的特点可以防止机器人在避开该墙的一侧后，又撞上该墙的另一侧.

2 基于人工力矩的机器人运动控制器

人工力矩概念由文献[11、12]等根据物理学中力的大小与方向共同决定力矩的基本思想而提出，其与人工势场力的基本区别是:人工力矩的大小不但与机器人和目标、障碍间的远近等这些在人工力场中通常被定义成吸引力或排斥力的距离有关，还与机器人的PMDline等相关有向线的方向有关，即还与“力的方向”有关.相对于人工势场力的主要优点是:人工势场力只能影响机器人的位置，而人工力矩可以根据系统需要，同时影响机器人的位置和PMDline方向或只影响其中的一个，从而为设计带来了更多的便利.

例如，本文设计的用于路径规划的吸引矩和排斥矩，其中吸引矩常在R的PMDline指向Powr时取得最大值，即通常只影响R的PMDline；排斥矩则总在R的PMDline背离相应危墙代表点时取得最大值，即仅影响R的PMDline.基于上述两种人工力矩函数设计的用于个体机器人路径规划的运动控制器，使R在大部分情况下，一方面沿合力矩增大的方向调整PMDline方向，另一方面则沿PMDline以最大步幅运动.即使在复杂的环境中，R也不会停止运动，即不会被陷住.所以基于人工力矩规划机器人路径，不会产生类似人工势场法中的“局部极小点”问题.

吸引矩与排斥矩函数具体设计如下.设当前时刻为tk，δθ为远小于π／2的正常数，函数

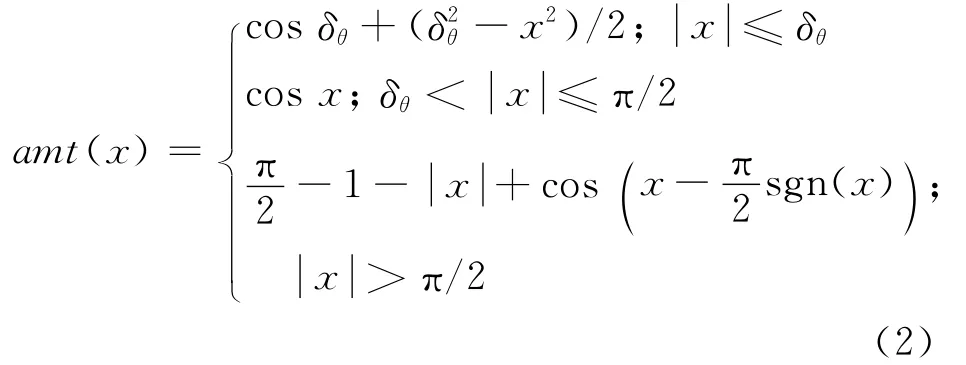
则Powr对R的吸引矩Ma(k)设计如下:

(1)如果Powr不是目标T或到PR的距离不小于Ds，则

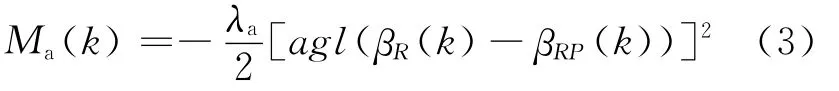
其中βRP(k)是Sd(PR，Powr)的方向角.λa是一常数，本文的取值方法是:如果tk时刻有一危墙代表点G，使得Sd(PR，Powr)到Sd(PR，G)的角的绝对值小于π／2，则λa＝0.5；否则λa＝0.8.按上述方法取λa的理由是:如果Sd(PR，Powr)到Sd(PR，G)的角的绝对值小于π／2，则向着Powr运动就有向着G运动的趋势，在此情况下吸引矩太大会使R的PMDline在吸引矩的作用下向障碍物方向偏转太多，从而使R的运动在障碍物前产生振荡.否则吸引矩大可以加快R趋向Powr的速度.

(2)如果Powr是目标T且到PR的距离小于Ds，则

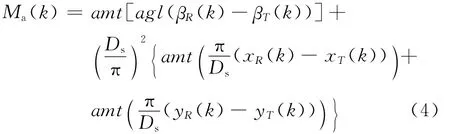
设G是tk时刻的一个危墙代表点，βGR(k)是Sd(G，PR)的方向角，DGR＝｜Sd(G，PR)｜，λp＝，则G对R的排斥矩Mp(k)设计为

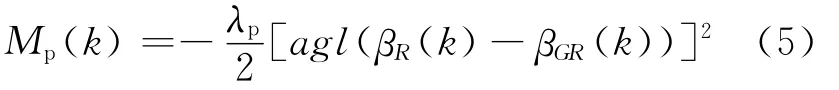
基于人工力矩的机器人运动控制器设计为

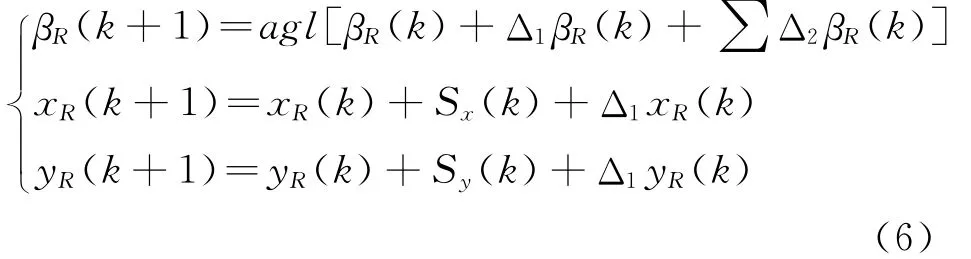
其中有关符号的意义和计算方法如下:

(1)(S(k)S(k))T是R在 时 间 段

xy(tktk＋1]内沿其 PMDline的运动量.计算方法是:如果Powr是T且到PR的距离小于Ds，则(Sx(k)Sy(k))T＝ (0 0)T；否则R将以最大步幅沿PMDline方向运动，即

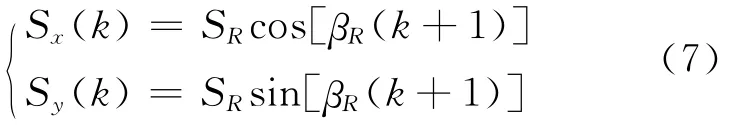
(2)(Δβ(k)Δx(k)Δy(k))T是能增加

1R1R1RR吸引矩的变化量，是吸引矩的梯度方向.设函数

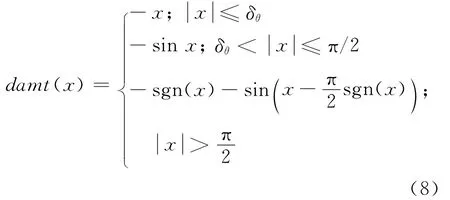
则据式(3)、(4)得

①如果Powr不是目标T或到PR的距离不小于Ds，则

②如果Powr是目标T且到PR的距离小于Ds，则

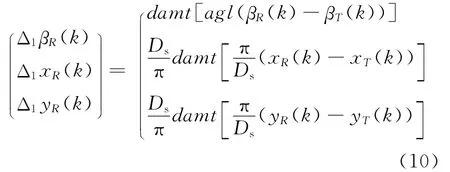
(3)当R没有危墙代表点时，∑Δ2βR(k)＝0.否则∑Δ2βR(k)是所有危墙代表点排斥矩梯度方向的和.设Δ2βR(k)是危墙代表点G对R排斥矩的梯度方向，则由式(5)得

从式(6)～(12)可以看出，基于人工力矩的运动控制器，使得R的运动速度，不会因为吸引矩和排斥矩的相互抵消而降低，因为排斥矩不影响机器人的运动速度.这一特点，不仅使得R不至于陷在某一局部极值点而不能自拔，即在人工力矩法中，不会出现类似“局部极小点”的问题；同时也增加了机器人的平均运动速度，从而加快了收敛速度.

将本文的人工力矩函数和运动控制器与文献[11、12]中相应的人工力矩函数和运动控制器相比可以发现，本文的人工力矩函数和运动控制器要简单得多，原理也更易懂.

尽管运动控制器(6)有许多优点，但如果存在一个危墙代表点G，满足

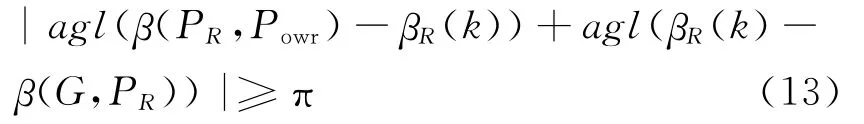
那么直接运用该运动控制器，则R就有可能不趋近Powr.

R不趋近Powr的原因，是因为不等式(13)意味着R的 PMDline到Sd(PR，Powr)的角与到Sd(G，PR)的角的符号相反，如图2所示，因此相应吸引矩与排斥矩的作用就可能相互抵消，R就可能继续沿原来PMDline的方向运动；如果R原来的PMDline不指向甚或背向Powr，那么在此情况下，R的运动就会不趋近Powr，或虽然趋近，但速度缓慢.

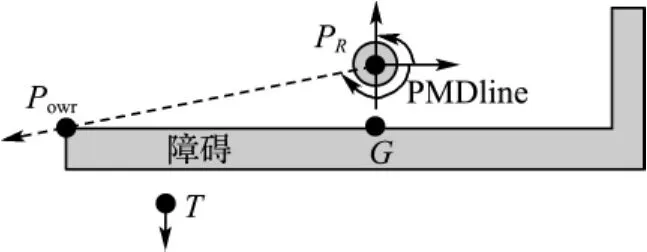
图2 R的PMDline背向PowrFig.2 R′s PMDline opposite to the Powr

改进方法就是在运用如式(6)所述的运动控制器前，先检查所有的危墙代表点，判断式(13)是否成立.如果都不成立，则直接运用；否则先令βR(k)＝β(PR，Powr)，即令R的 PMDline指向Powr，然后再运用前述控制器.经过上述改进后发现，在当Sd(PR，Powr)不被知识障碍墙阻断时，基于人工力矩的运动控制器总能使R逐渐趋近Powr.

3 最优路径代表点求解及局部路径规划的基本步骤

首先探讨Powr的求解方法，因为如果不求得Powr，则基于人工力矩的运动控制器就无法进行，路径优化也无从谈起.为了方便论述Powr的求解，下面给出两个新概念.

定义5 设F是广义可行路径上的一个点，A是知识障碍墙Σ上的一个点.(1)如果 (Lr(F，A)，－FA)∩Σ＝且Lr(F，A)不被Σ阻断，那么称Lr(F，A)为从F到Σ的单向切线，A为切点.(2)当 (Lr(F，A)，－FA)∩Σ不为空时，设A＊为其中距A最近的点.如果AA＊与Σ的一部分能形成一条将F和T分开的闭合曲线，那么Lr(F，A)为从F到Σ的闭合切线，A为切点，A＊为闭合点.

如在图3中，Lr(PR，A4)是从PR到Σ1的单向切线，A4为切点；Lr(PR，A1)是从PR到Σ1的闭合切 线，A1为 切 点、F1为 闭 合 点；Lr(A1，A2)和Lr(A2，A3)则分别是从A1、A2到Σ1的闭合切线.

为了简化Powr的求解，在运动过程中，R还会按照下述规则在环境中设置人工障碍线:(1)当PRT同时被知识障碍墙Σ1、Σ2阻断时，设A1、A2分别为PRT与Σ1、Σ2的交点，那么A1A2将被设置为一条人工障碍线；(2)当PRT仅被Σ1阻断时，设A1为从PR到Σ1的单向或闭合切线的切点.如果PRA1被Σ2阻断，那么设A2为PRA1与Σ2交点中，距A1最近的点，则A1A2将被设置为一条人工障碍线.

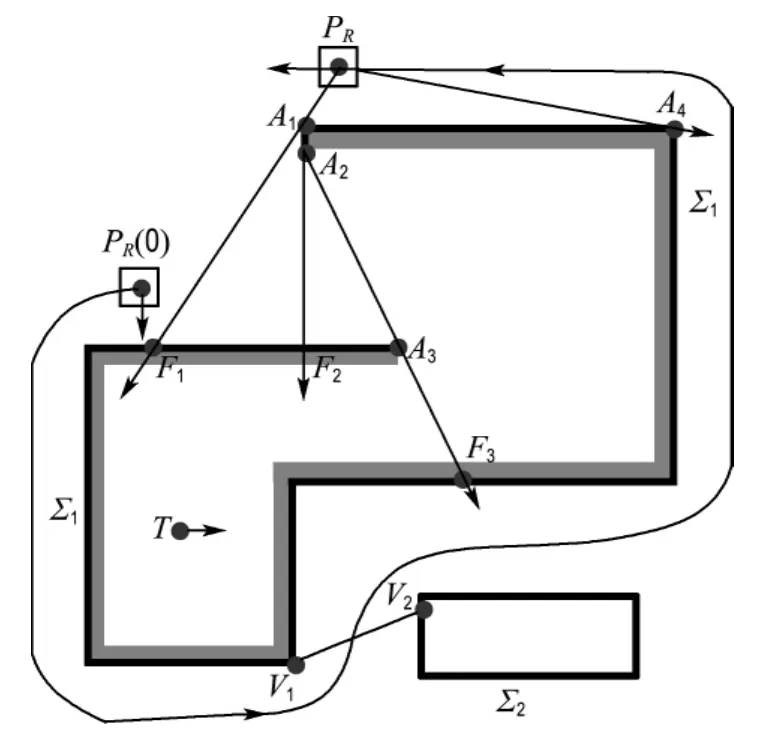
图3 单向切线、闭合切线与人工障碍线Fig.3 Single－direction tangents，closed tangents and artificial obstacle segments

如在图3中，V1V2就是R设置的人工障碍线.设置人工障碍线的主要根据是“沿墙走”方法中尽量不让机器人往回走的原则.因为如果A1A2是当前时刻设置的人工障碍线，则根据设置方法知，A1A2在当前时刻不能被R探测，但由于A1、A2都在知识障碍墙上，所以A1A2在过去一定可以被R探测到.上述分析说明了R从曾经距A1A2较近的位置运动到了现在距A1A2较远的位置.所以把A1A2设置成人工障碍线，防止R向A1A2运动就可以防止R往回走，从而在一定程度上可以保证全局收敛性.

虽然通常情况下，人工障碍线被当作知识障碍墙的一部分处理，但如果人工障碍线的设置导致形成一条能将R、T分开的闭合知识障碍墙，则该墙上的所有人工障碍线都会被撤除.

结论1 如果R在当前时刻不能设置人工障碍线，那么，(1)PRT最多被一条知识障碍墙阻断；(2)设PRT被知识障碍墙Σ阻断，A1为从PR到Σ的单向或闭合切线的切点，那么PRA1不会被任何知识障碍墙阻断.

结论2 如果PRT被知识障碍墙Σ阻断且从PR到Σ有一条闭合切线，那么该闭合切线的切点为Powr.

结论3 当PRT被知识障碍墙Σ阻断，从PR到Σ有两条单向切线时，设两单向切线的切点分别是A1、Q1，那么根据下面算法1可以得到一条记为WA1的路径PRA1A2…AnT.

算法1 (求路径WA1)

Step 1 令Ai＝A1，A0＝PR.

Step 2 如果AiT没有被Σ阻断，那么停止运算，Ai、T为WA1上的最后两个节点；否则转Step 3.

Step 3 如果R有一条从Ai到Σ的闭合切线，则Ai＋1就是该闭合切线的切点；令Ai＝Ai＋1，然后返回Step 2.否则转Step 4.

Step 4 如果Ai＝A1，那么A2就是从A1到Σ满足如下条件单向切线的切点:该切线与Lr(PR，Q1)没有交点.否则Ai＋1就是从Ai到Σ满足如下条件单向切线的切点:该切线与Lr(Ai－2，Ai－1)没有交点.令Ai＝Ai＋1，然后返回Step 2.

结论4 当PRT被知识障碍墙Σ阻断且从PR到Σ没有闭合切线时，则(1)R有两条从PR到Σ的单向切线；(2)设两条单向切线的切点分别是A1、Q1，那么如果WA1、WQ1都是广义可行路径，则其中有一条必是以PR、T为端点的最短广义可行路径；Powr必是A1、Q1中的一个.

综合前面的讨论，得到了一个计算Powr的算法，即算法2.

算法2 (计算Powr的近似算法)

Step 1 如果PRT未被知识障碍墙阻断，那么T就是Powr；否则转Step 2.

Step 2 设PRT被知识障碍墙Σ阻断.如果从PR到Σ有一条闭合切线，则该闭合切线的切点为Powr；否则转Step3.

Step 3 计算出从PR到Σ的两条单向切线的切点，设分别是A1、Q1.

Step 4 运用算法1，分别得到WA1、WQ1；然后计算出｜WA1｜、｜WQ1｜.

Step 5 如果｜WA1｜＜｜WQ1｜，则A1是Powr；否则Q1是Powr.

据算法2得到的Powr不一定位于以PR、T为端点的最短广义可行路径上，原因是WA1、WQ1不一定是以PR、T为端点的广义可行路径，不一定满足结论3的条件，所以算法2只是一个近似算法.但据算法2得到的解，对路径仍有显著的优化效果.

算法2在最坏情况下的计算量，就是要分别得到WA1、WQ1.设知识障碍墙中边数最多知识障碍墙的节点数为m，则根据算法1知:最多经过m步的计算，就可以得到WA1／WQ1；所以算法2的时间复杂度为O(2m).

综合算法2和前面关于机器人运动控制器的讨论，得到了算法3.

算法3 (个体机器人局部路径的规划)

Step 1 给定系统参数值；对R、T及环境初始化；令tk＝t0.

Step 2 判断当前时刻能否设置人工障碍线.如果能够，则设置好人工障碍线.

Step 3 调用算法2，得到Powr；同时得到所有危墙代表点.

Step 4 对每一个危墙代表点，判断式(13)是否成立；一旦式(13)成立，即令βR(k)＝β(PR，Powr).

Step 5 在基于人工力矩运动控制器的控制下，R运动一步到达下个时刻的位置.

Step 6 如果R还没有到达T，则更新知识障碍墙集，然后转Step 2.如此循环，直到到达T，结束程序.

定理1 如果运用算法3规划个体机器人的路径，那么在本文所给条件下，R能最终到达T，即系统具有可达性.

证明 根据算法3和前面的讨论，可以得到如下结论:如果tk时刻没有探测到新的障碍点，没有也不能设置人工障碍线，那么在不考虑那些不能阻断PR(k－1)T与PR(k)T的知识障碍墙的条件下，以PR(k)、T为端点的最短广义可行路径一定比以PR(k－1)、T为端点的最短广义可行路径短.得到上述结论的理由是R会逐渐靠近Powr，从而在环境没有变化的情况下，相应的最短广义可行路径会缩短.

根据上述结论可以推出，在最坏情况下:当所有可能被探测到的障碍点全都被探测，所有的知识障碍墙都通过人工障碍线连成了一条，那么环境就不可能再变化，以PR、T为端点的最短广义可行路径就会逐渐缩短并最终为零，即R能最终到达T，所以系统具有可达性.证毕.

4 仿真结果与分析

下面给出一个比较典型的仿真，以证明本文所给方法的可行性与有效性.在该仿真中，系统参数值如表1所示；R不具备任何先验的环境信息，要求它仅依靠传感器的实时探测和运动过程中积累的环境知识，运用本文所提方法来规划出一条到达目标T的路径.

表1 参数值Tab.1 Values of parameters

仿真结果如图4所示，其中图4(a)、(b)分别显示了R在运动79步和147步后的状态.从图4可以看出，R在障碍物前的运动像“沿墙走”方法一样光滑；但显然又不是简单的“沿墙走”.如当R在M点时，发现如果继续近似沿1号障碍的墙走，有可能要走更长的路径，就转向墙的另一端运动.如此调整显然极大地缩短了R的运动路径.同时从图4可以看出，R安全地通过了2号与3号障碍间等狭窄通道，准确地到达了距障碍很近的目标，在整个运动过程中没有出现被陷住的现象.而上述结果，是人工势场法难以得到的，所以人工力矩法相对于人工势场法有显著的优势.

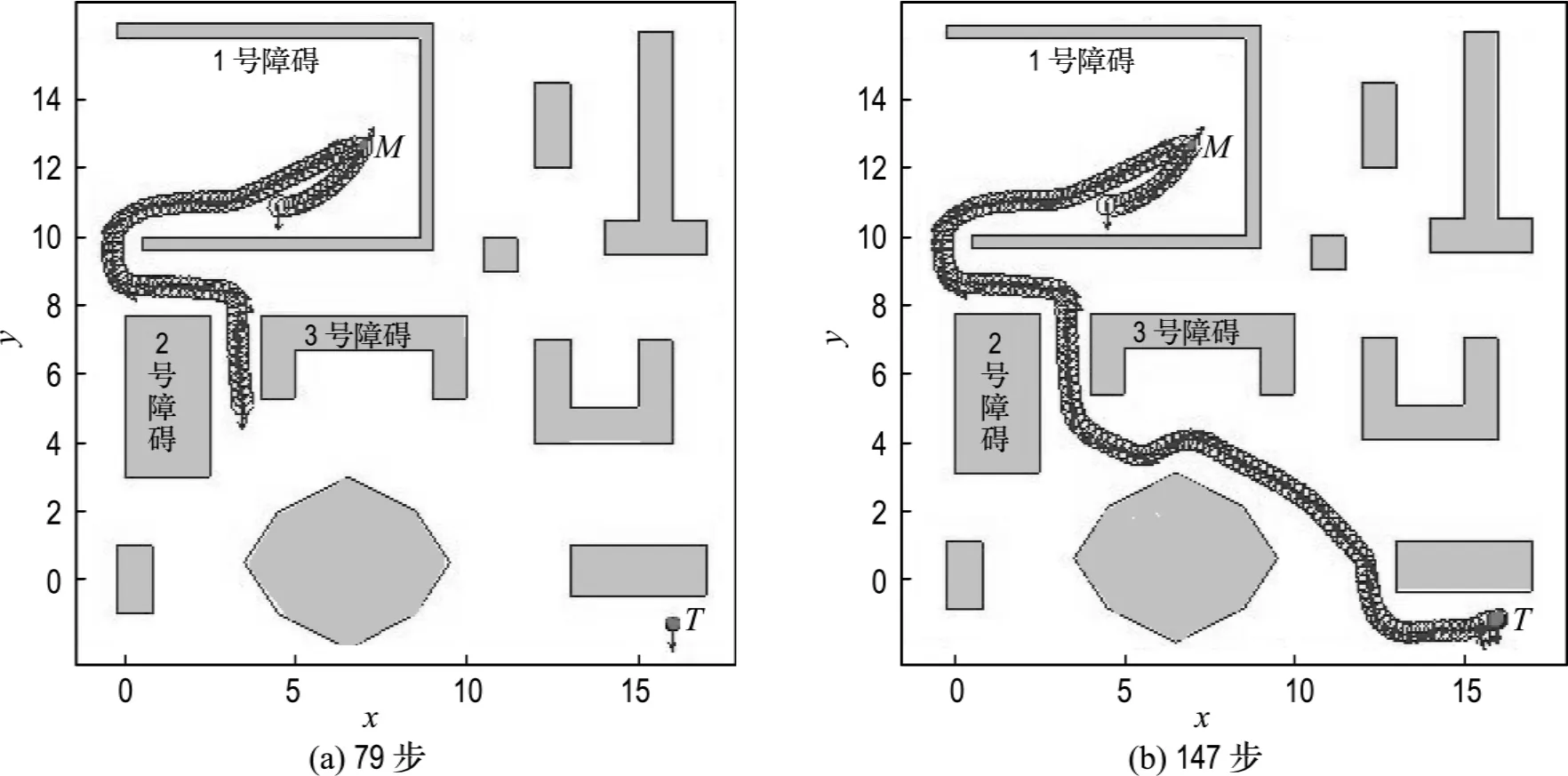
图4 复杂环境中个体机器人的路径规划Fig.4 Path planning of single robot in a complicated environment

5 结 语

利用当前全部环境知识而得到的最优路径代表点，不但可以帮助机器人优化路径和最终到达目标，且有存储量小，不需要预处理环境等优点.最优路径代表点的近似计算方法，虽然不一定总能得到精确解，但却有时间复杂度低、具有良好优化效果的特点.基于人工力矩的运动控制器，继承了人工势场法的实时性强、计算容易等优点，而使机器人不会在复杂环境中被陷住，且能控制机器人准确地到达距障碍很近的目标.

下一步将研究更一般环境中，最优路径代表点的计算方法及如何运用本文所提方法解决多机器人的避碰和路径规划等问题.

[1]GE S S，LAI X，MAMUM A A.Boundary following and globally convergent path using instant goals[J].IEEE Transactions on Systems，Man，and Cybernetics，Part B:Cybernetics，2005，35(2):240－254

[2]ZHU Yi， ZHANG Tao，SONG Jing－yan. An improved wall following method for escaping from local minimum in artificial potential field based path planning [C]／／ Proceedings of Joint 48th IEEE Conference on Decision and Control and 28th Chinese Control Conference.Shanghai:IEEE Press，2009:6017－6022

[3]NG J，BR UNL T.Performance comparison of bug navigation algorithms [J].Journal of Intelligent and Robotic Systems，2007，50(1):73－84

[4]RIMON E， KODITSCHEK D E. Exact robot navigation using artificial potential functions [J].IEEE Transactions on Robotics and Automation，1992，8(5):501－518

[5]GE S S，CUI Y J.New potential functions for mobile robot path planning [J].IEEE Transactions on Robotics and Automation，2000，16(5):615－620

[6]KIM Dong－hun.Escaping route method for a trap situation in local path planning [J].International Journal of Control，Automation，and Systems，2009，7(3):495－500

[7]HUANG H P，CHUNG S Y.Dynamic visibility graph for path planning[C]／／Proceedings of IEEE／RSJ International Conference on Intelligent Robots and Systems.Sendal:IEEE Press，2004:2813－2818

[8]LIU Y H，ARIMOTO S.Proposal of tangent graph and extended tangent graph for path planning of mobile robots [C]／／ Proceedings of IEEE International Conference on Robotics and Automation.Sacramento:IEEE Press，1991:312－317

[9]TAKAHASHI O， SCHILLING R J. Motion planning in a plane using generalized Voronoi diagrams [J].IEEE Transactions on Robotics and Automation，1989，5(2):143－150

[10]SUD A，ANDERSEN E，CURTIS S，etal.Realtime path planning in dynamic virtual environments using multiagent navigation graphs [J].IEEE Transactions on Visualization and Computer Graphics，2008，14(3):526－538

[11]XU Wang－bao，CHEN Xue－bo.Artificial moment method for swarm－robot formation control [J].Science in China Series F:Information Science，2008，51(10):1521－1531

[12]徐望宝，陈雪波.一种基于人工力矩的动态队形控制方法[J].控制理论与应用，2009，26(11):1232－1238