基于6－UHU型并联机构的动载坦克模拟器螺旋耦合补偿

丛 明， 伍 英 华， 刘 冬， 杜 宇， 温 海 营， 于 俊 发

(1.大连理工大学 精密与特种加工教育部重点实验室，辽宁 大连 116024；2.65053部队，辽宁 大连 116031)

0 引 言

自Stewart[l]在1965年提出一种新型的六自由度空间并联机构以来，并联机构被运用于各种模拟器.基于并联机构的动载坦克模拟器是模拟坦克作战的设备，可以代替真实坦克进行驾驶员和车炮长的培训.而且其因动态性能好、仿真度高、训练效率高、培训周期短，不受天气、场地和时间的限制等优点[2、3]，在世界各国得到广泛应用.

由于六自由度并联机构的多输入多输出非线性特点，输入值的动态误差直接影响运动平台的动态性能，导致运动平台在运行过程中产生抖动.这不仅会降低机构控制的精准度，缩短机构的使用寿命，同时也无法保证机构与上位机图形软件的实时性.针对并联机构运动误差及误差补偿的方法有许多种.Abdellatif等[4、5]分析了从动副的摩擦特点和摩擦对机构运动及控制的影响.Meng等[6]对并联机构的测量误差进行了补偿，Yang等[7]提出了动态重力补偿控制方法，Kevin等[8]分析了杆长误差对并联机构的影响，王伟等[9]对液压并联机构耦合特点进行了研究，李强等[10]提出电液伺服并联机构干扰力补偿方法.

目前对于电动并联机构耦合现象的分析及研究却只有少数学者提及.张歆[11]曾运用D－H表示法对并联机构支链进行补偿，但该方法需建立8组坐标系，过程复杂，这将无法保证运动平台与上位机的实时性.建立简洁的耦合补偿以保证控制的实时性成为研究的难点.另外，使用检测仪器直接检测运动平台运动特性较为困难，学者在进行方法验证时多采用仿真实验方法[12～14].该方法简化影响机构运动的某些因素，如电机及控制器等，实验结果常与实际并联平台运动存在偏差.

本文以实验室自行研制的动载坦克模拟器为研究对象，利用螺旋理论对6－UHU型并联机构螺旋耦合现象进行分析，提出一种基于6－UHU型并联机构的动载坦克模拟器螺旋耦合补偿的新方法，将繁琐的坐标系变化转变为空间向量的变化，简化运算过程，满足控制实时性.同时，采用机构－模型联合运动实验方法，提取实际控制曲线，对新的补偿方法进行验证.

1 动载坦克模拟器耦合性分析

图1为动载坦克模拟器样机.

6－UHU型动载坦克模拟器上下平台间通过6根由上虎克铰、螺旋副、下虎克铰组成的支链联接，图2为6－UHU型动载坦克模拟器本体模型.选取其中一个支链利用螺旋理论[15]对其耦合性进行分析.

图1 动载坦克模拟器样机Fig.1 Dynamic load tank simulator test prototype

图2 6－UHU型动载坦克模拟器本体模型Fig.2 Model of 6－UHU dynamic load tank simulator

首先假设支链螺旋副在运动过程中不存在耦合现象，即螺旋副只会产生沿杆长方向的移动，建立坐标系如图3所示.

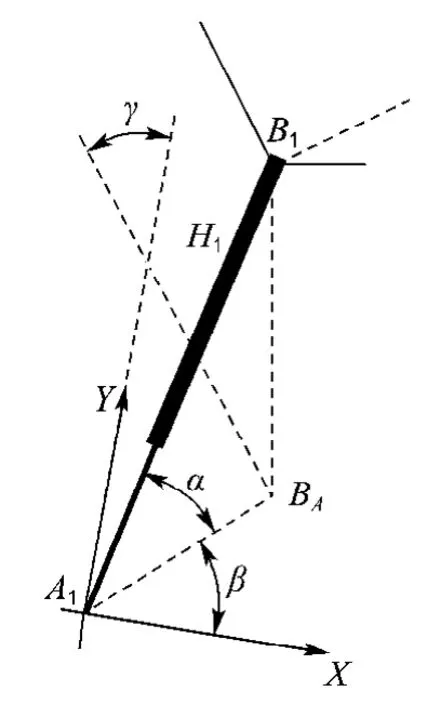
图3 支链A1H1B1坐标系Fig.3 Coordinate system of leg A1H1B1

这样下虎克铰A1可以分解为两个正交的转动副，其Plücker坐标为

设螺旋副H1与面XY之间的夹角为α，投影线A1BA与X轴之间夹角为β，则螺旋副H1的Plücker坐标为

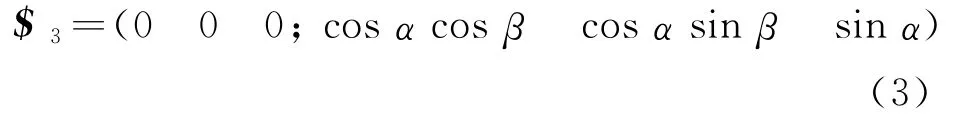
同样上虎克铰分解为两个正交转动副，记支链杆长为L1，上下虎克铰安装夹角为γ.上虎克铰中心点B1(lcosαcosβlcosαsinβlsinα).可求得上虎克铰两旋量＄4、＄5分别为

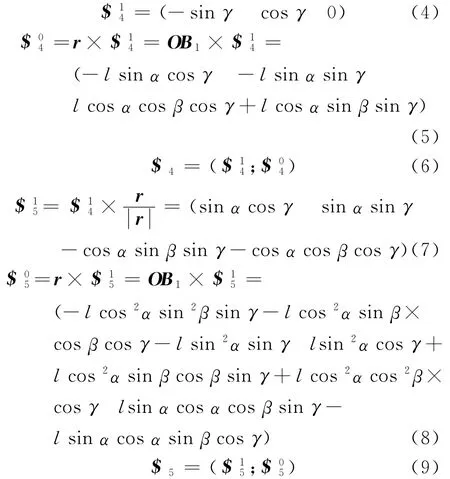
支链A1H1B1的运动螺旋系可以表示为

则支链A1H1B1的反螺旋系仅含一个旋量＄rA1H1B1＝(LMNPQR)，即支链存在一个力约束.由螺旋理论可知螺旋系与反螺旋系旋量间的互异积为零，即有

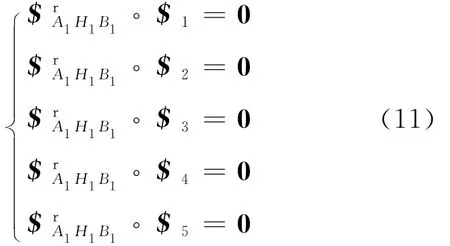
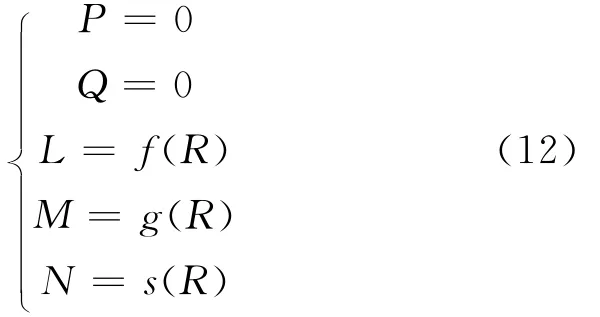
可以求得其中f(R)、g(R)、s(R)是以R为自变量的函数.同理其余5个支链各存在一个约束.

对于六自由度并联机器人，利用机构自由度的计算公式可以推算出每个支链的自由度至少为6[16].依据假设推算出每个支链各存在一个约束，自由度为5，则并联机器人运动平台自由度小于6.但实际动载坦克模拟器的自由度为6，理论假设与实际产生矛盾，各支链中必存在螺旋耦合运动.

螺旋副存在螺旋耦合运动时，支链螺旋系新增旋量:

此时可求得支链的反螺旋系为

因而，该支链不对末端执行器产生任何约束，其他支链亦然.运动平台能够完成三维空间中的各个动作，与实际相符.

因此单支链螺旋副随上平台运动存在螺旋耦合运动.

2 螺旋耦合补偿

以下平台六虎克铰分布圆心Oa为原点建立静坐标系OaXaYaZa，以上平台六虎克铰分布圆心Ob为原点建立动坐标系ObXbYbZb，如图2所示.各轴杆长在静坐标系中向量为

对动载坦克模拟器某一支链模型建立坐标系，如图4所示.

以上平台铰点中心Omi为圆心建立上铰点坐标系OmiXmiYmiZmi(i＝1，…，6)，Zmi轴、Xmi轴单位向量表示为

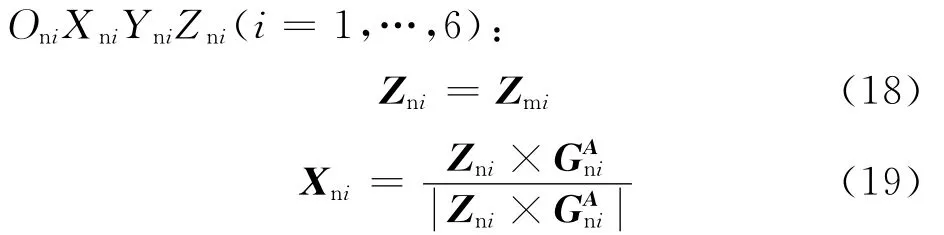
G为下虎克铰在静坐标系中的安装外向量.

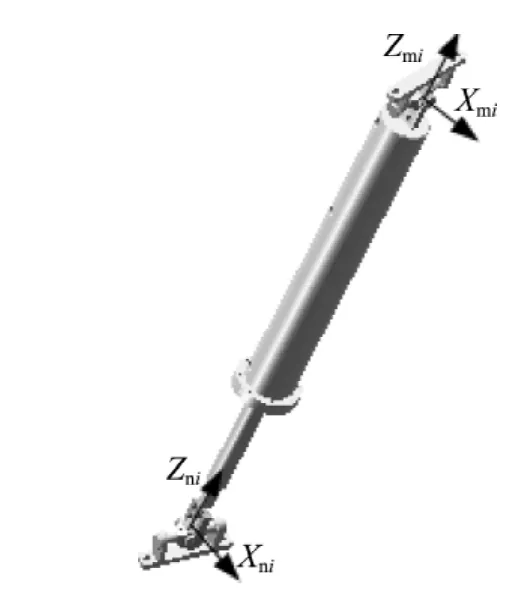
图4 动载坦克模拟器单支链模型Fig.4 One leg model of dynamic load tank simulator

以此建立的上铰点坐标系和下铰点坐标系在动载坦克模拟器运动时只存在绕杆长即Z轴方向的旋转和移动，旋转角度就为所要求解的螺旋耦合角度，记为ψi:

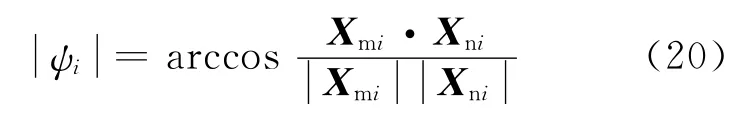
Xmi×Xni与同向记ψi为正，反之为负.

螺旋耦合角速度

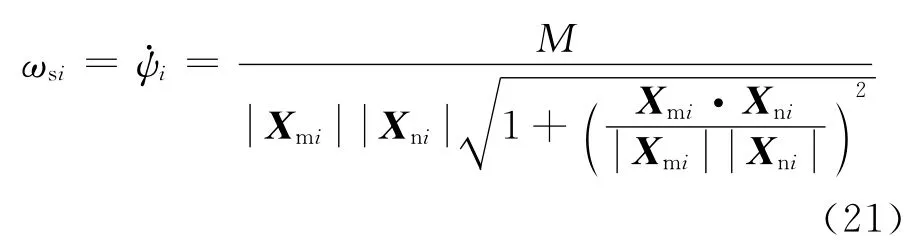
其中

J为平台广义速度到支链杆伸缩速度的雅可比矩阵.

第i杆的伸缩长度与理论差值为

Da为螺旋副导程.

经补偿后的实际控制杆长为

Δpi为动载坦克模拟器上一位姿杆长差值.

3 机构－模型联合运动实验

3.1 实验方法对比

本文对比电机理论控制曲线和机构－模型联合运动实际提取曲线.图5是以动载坦克模拟器绕Z轴方向作幅值30°、周期4.3s的正弦曲线运动为运动过程，提取的1、2杆耦合补偿前两种方法的控制脉冲曲线.

图5 理论与实验脉冲曲线Fig.5 Theoretical and experimental pulse curves

理论控制曲线与机构－模型联合运动实验控制曲线存在差别的原因有以下两个方面:①运动控制器的影响.理论控制曲线忽略了实际运行中难以控制和计算的因素，如运动控制器接受、运算数据速度及发送指令曲线，造成曲线差别.②电机运动特性的影响.驱动电机的某些性能参数具有随机性，使理论控制曲线与机构－模型联合运动控制曲线存在差别.

机构－模型联合运动实验以实际模拟器驱动曲线作为驱动输入，使模拟实验更接近实际情况，有利于对动载坦克模拟器运动性能的研究.

3.2 实际控制曲线提取

6－UHU型动载坦克模拟器能够模拟坦克在运行过程中的俯仰、侧倾、偏转、颠簸、侧滑及打炮后作6种动作，真实再现模拟器实际演习动作，对坦克驾驶员和车炮长的训练更具真实感.本文以图1所示的动载坦克模拟器为研究对象，运动中负载为2t，表1为其几何参数.

以动载坦克模拟器为研究对象作特定运动，机构－模型联合运动实验把驱动电机位置反馈实际值作为所建模型驱动，运动模型将重现动载坦克模拟器实际动作，检测动平台各项运动指标.图6为机构－模型联合运动实验原理.图7为螺旋耦合补偿前后提取的1、2杆驱动电机转动速度.

表1 6－UHU型动载坦克模拟器几何参数Tab.1 Geometric parameters of 6－UHU dynamic load tank simulator

图6 机构－模型联合运动实验原理图Fig.6 Mechanism－model combined motion experiment schematic diagram

图7 电机速度实验曲线Fig.7 Experimental curves of motor speed

4 实验结果

实验提取动载坦克模拟器绕Z轴方向作幅值为30°、周期4.3s的正弦曲线运动时电机的实际控制曲线，以此作为模型输入研究螺旋耦合补偿前后动载模拟器的运动情况.表2数据表明Z轴转动能够完成预期指令轨迹，模拟器在非指令方向Z轴移动产生偏差.图8(a)、(b)分别为Z轴转动角度φZ和Z轴移动距离z，图8(c)、(d)分别为Z轴移动速度vZ和加速度aZ.

表2 动载坦克模拟器运动误差Tab.2 Motion error of dynamic load tank simulator

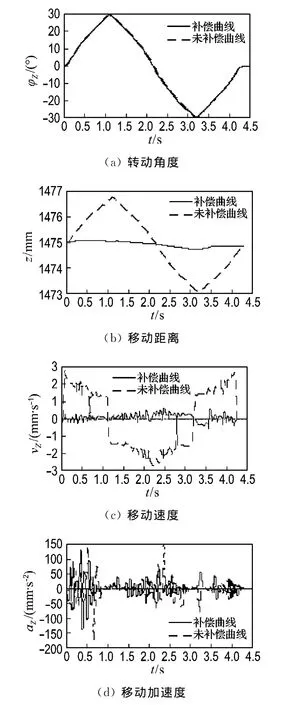
图8 Z轴转动角度和移动距离、速度、加速度Fig.8 Rotational angle and moving distance，speed and acceleration of Zaxis

实验结果表明，在指令运动方向动载坦克模拟器运动曲线偏差较小，模拟器能够按照指令预期幅值和周期运动，螺旋耦合影响轻微；而在非指令方向动载坦克模拟器出现与指令不符的运动，模拟器在Z轴出现非指令运动，造成模拟器抖动.通过对动载坦克模拟器螺旋耦合补偿，非指令Z方向运动接近指令预期值，误差速度绝对值降低82%；误差加速度值减小25%，最大值由175 mm／s2减小为140mm／s2.螺旋耦合补偿有效地降低了动载坦克模拟器非指令方向运动幅度，减小了不必要的振动，使运动更为平滑.

同理，实验以X轴和Y轴转动作为研究过程，实验结果表明模拟器分别在X轴和Y轴方向出现移动，螺旋耦合补偿后非指令方向运动接近预期值.基于软件保护方面考虑，控制器限制电机的最高转速，故而X轴和Y轴运动时间较预期有所延长.X轴、Y轴移动距离如图9、10所示.

图9 X轴移动距离Fig.9 Movement distance on Xaxis

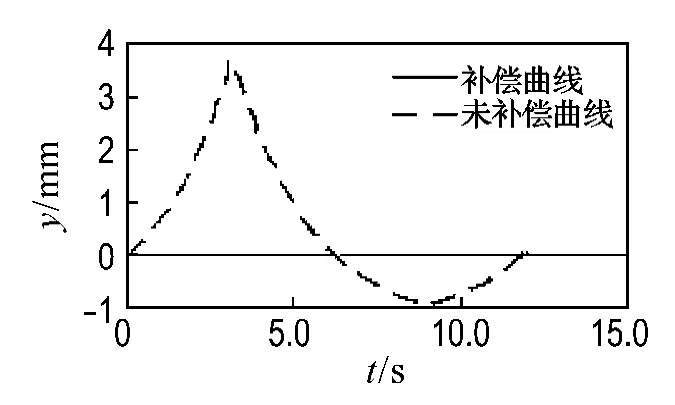
图10 Y轴移动距离Fig.10 Movement distance on Yaxis

5 结 论

(1)6－UHU型动载坦克模拟器支链中存在螺旋耦合运动.对于支链为UHU型的六自由度并联动载坦克模拟器，其支链耦合运动是可以控制的.在逆运动学基础上，转变两坐标系间向量以计算螺旋耦合角度和角速度，使动载坦克模拟器运动中存在的螺旋耦合得以补偿.

(2)通过对电机控制实际曲线的提取，机构－模型联合运动实验考虑了影响动载坦克模拟器控制曲线的两个因素:运动控制器和电机，使实验的真实性与可靠性大大提高.

(3)实验结果分析表明，螺旋耦合补偿通过减小动载坦克模拟器在非指令方向的运动，降低抖动幅度，提高其运动平稳性和准确性，避免了对运动机构额外的磨损，从而延长了动载坦克模拟器的使用寿命.

[1]STEWART D. A platform with six degree of freedom [C]／／Proceedings of Institute of Mechanical Engineering.London:IME，1965:371－386

[2]于俊发，丛 明，王智勇，等.坦克驾驶模拟器的运动仿真算法与实现[J].计算机仿真，2007，24(7):305－308

[3]DASGUPTA B， MRUTHYUNJAYA T S.The Stewart platform manipulator:a review [J].Mechanism and Machine Theory，2000，35(1):15－40

[4]ABDELLATIF H，HEIMANN B.On compensation of passive joint friction in robotic manipulators:modeling，detection and identification [C]／／ Proceedings of the IEEE International Conference on Control Applications.Munich:IEEE，2006:2510－2515

[5]ABDELLATIF H，GROTJAHN M，HEIMANN B.Independent identification of friction characteristics for parallel manipulators[J].Journal of Dynamic Systems，Measurement and Control，2007，129(3):294－302

[6]MENG Z，CHE R S，HUANG Q C，etal.The direct－error－compensation method of measuring the error of a six－freedom－degree parallel mechanism CMM [J]. Journal of Materials Processing Technology，2002，129(1－3):574－578

[7]YANG Chi－fu，HUANG Qi－tao，JIANG Hong－zhou，etal.PD control with gravity compensation for hydraulic 6－DOF parallel manipulator[J].Mechanism and Machine Theory，2010，45(4):666－677

[8]KEVIN C， TATSUO A. A prototype parallel manipulator :kinematics，construction，software，workspace results，and singularity analysis [C]／／Proceedings－IEEE International Conference on Robotics and Automation.Sacramento:IEEE，1991:566－571

[9]王 伟，谢海波，傅 新，等.大型液压Stewart平台动态耦合特性[J].机械工程学报，2007，43(9):12－15

[10]李 强，王宣银，程 佳.基于逆动力学模型的Stewart平台干扰力补偿[J].机械工程学报，2009，45(1):14－19

[11]张 歆.6＿THHT并联机器人动力学分析及控制技术研究[D].南京:南京理工大学，2006

[12]MA Jian－ming，HE Jing－feng，XIONG Hai－guo，etal. Simulation of coupling characteristic of hydraulically driven Stewart platform based on dynamics model[C]／／2008International Workshop on Modeling，Simulation and Optimization.Hong Kong:IEEE，2008:88－92

[13]IQBAL S， BHATTI A I， AHMED Q.Determination of realistic uncertainty bounds for the Stewart platform with payload dynamics [C]／／17th IEEE International Conference on Control Applications.San Antonio:IEEE，2008:995－1000

[14]刘 胜，李晚龙，杜延春，等.潜器Stewart平台动力学仿真[J].哈尔滨工业大学学报，2009，41(9):249－255

[15]黄 真，赵永生，赵铁石.高等空间机构学[M].北京:高等教育出版社，2006:65－73

[16]陈 峰，费燕琼，赵锡芳.六自由度并联机器人的支链选取[J].机器人，2005，27(5):396－399