基于ERSM的涡轮机匣径向变形动态概率分析

费成巍，白广忱

（北京航空航天大学能源与动力工程学院，北京 100191）

0 引言

涡轮机匣的径向变形对叶尖间隙控制有重要影响，对机匣径向变形进行合理有效地分析具有重要意义。国内外的许多研究机构用分析软件对机匣径向变形进行数值分析，取得了很多研究成果[1-3]。然而，这些成果都是采用确定性分析方法，忽略了径向变形各方面影响因素的随机性，具有很大的盲目性。因此，为了更客观准确地描述机匣径向变形的变化规律，改善运行间隙设计和控制的合理性，应考虑多个随机因素和载荷的随机性对机匣径向变形的影响。这相应要求机匣径向变形的确定性分析亟待转变为概率分析。

概率分析已在许多领域广泛应用[4-6]，但目前还未应用于航空发动机可靠性分析。如果对机匣径向变形进行概率分析，不但可以根据随机参量的分布特征得到机匣径向变形的概率分布，也可以根据机匣径向变形设计要求确定随机参量特征，有利于改善机匣设计优化和叶尖间隙控制，同时也便于提高发动机的效率和性能。张春宜、白广忱等[7]提出的柔性机构可靠性优化的极值响应面法（ERSM），能在不降低计算精度的前提下大大提高计算效率，为机匣径向变形的概率分析提供新的思路。

本文将ERSM应用到涡轮机匣径向变形动态概率分析中，提出了动态概率分析的极值响应面法。

1 基本理论

1.1 传统方法

传统概率分析方法有Monte Carlo法（MC法或MCM）和响应面法（RSM）[8]，以及其改进方法[7,9-11]。MCM是通过随机抽样的手段，解决未知极限状态方程情况下，进行可靠性分析的最简单直接的方法。其计算精度很高，但计算时间很长，效率低。RSM是通过一系列确定试验拟合1个响应面来模拟真实极限状态曲面。若用响应面式（1）来描述系统输出响应Y和随机参数X=[X1,X2,…，Xr]关系，通过随机抽样得到随机变量的N个样本值，再对N个样本值计算得到系统响应的1组样本值（z1,z2,…zs），求解响应面函数未知系数，得到该系统函数，进而用该响应面代替有限元模型进行概率分析。

式中：a0、bi、cij（i=1,…，r；j=1,…,r）分别为常数项、1次项和2次项的待定系数。

RSM的计算效率虽比MCM有所提高，但对于非线性复杂结构的动态概率分析，计算量大大增加，且计算效率仍很低。

1.2 动态概率分析的极值响应面法

针对以上问题，本文提出动态概率分析的极值响应面法（ERSM），其基本原理是：首先，用MCM小批量抽取输入参数随机样本，对每个抽样样本在分析时域[0,T]内求解有限元模型，得到系统在[0,T]内的动态输出响应。再将全部抽样输入样本对应的动态输出响应在[0,T]内的极值作为新的输出响应，构造[0,T]内反映输入参数与极值输出之间关系的函数。选取输入随机变量及对应的输出极值响应数据代入响应面函数（如式（1）），确定其系数。其次，用该响应函数代替有限元模型计算系统的动态极值输出响应，从而进行系统的概率分析。该方法在动态概率分析时，不计算系统每一时刻的输出响应，只计算分析时域[0,T]内不同输入随机变量对应的输出响应的极值，从而进行系统的概率分析。其模型如图1所示。可以看出，ERSM是将原来非线性复杂动态系统概率分析的随机过程问题转化为随机变量问题，由此极大地减少了计算时间，提高了计算效率，使得从前一些不可能实现的概率分析问题成为可能。

图1 有限元极值响应面法动态概率分析流程

1.3 ERSM的数学模型

设某有限元模型第j组输入样本为X（j），在[0，T]时域内的输出响应为，该响应在[0，T]时域内的最大值为如图2所示。将不同输入样本在[0,T]内输出响应的最大值构成的集合的全部数值点拟合的曲线作为新的输出响应曲线Y，并称为极值响应曲线，则 X（j）与Y的函数关系可以表示为

写成响应面函数形式

式中：a0为常数；B为1次项系数向量；C为含有交叉项的2次项系数上（下）三角矩阵；X为输入变量向量。

式（3）被称为极值响应面函数。由该函数确定的输入输出关系曲线称之为极值响应曲线。其中

式中：j=1,2….M；M为样本点数；下标k为输入变量数。

在求解极值响应面函数系数时，在极值输出响应中选取足够数量的试验点，将试验点的数据代入式（3）中，确定极值响应面函数的系数 a0、B、C，得到极值响应面函数的表达式。然后用该极值响应面函数代替有限元模型进行相应的概率分析，这种方法就是ERSM，属于全局响应面法。

1.4 概率分析方法

概率分析是用来评估模型的输入参数或假设条件的不确定性对于结果的影响，进而确定结果的分布情况，这样能避免过设计，可以对构件在工作情况下的安全可靠性给出定量的结果，以保证其安全性。在确定极值响应面函数后，若某系统要求最大输出为δmax，则可根据式（3）得到极限状态函数

由上式可知，H（X）≤0为失效模式；反之为安全模式。若极限函数H（X）的均值和方差分别为μH和DH，且服从正态分布，则其可靠性指标β和可靠度R为[7]

对于任意分布函数Φ（·）都可以用MCM计算可靠度，进而可求出各随机变量的灵敏度[8]。

2 涡轮机匣确定性分析

2.1 有限元模型

某型发动机高压涡轮机匣的简化结构如图3（a）所示，图中的高压涡轮衬环是1个敏感元件，膨胀和收缩带动机匣径向变形，从而改变叶尖间隙，因此，主要对内层的涡轮衬环进行分析。将机匣衬环的结构简化为圆筒结构，建立轴对称模型，取轴截面研究对象，有限元模型如图3（b）所示，在模型左端固定轴向的自由度，防止产生轴向的刚体位移。

在分析之前，选取发动机从地面启动—慢车—爬升—巡航这一段[0,215 s]作为计算范围，取12个关键点作为计算点，计算载荷谱如图4所示。考虑动态温度影响、机匣材料的非线性导热系数和非线性膨胀系数，对其进行动态热结构耦合分析。

图4 计算采用的载荷谱

2.2 随机变量选取

机匣在加工和实际使用中其材料参数和工作条件都存在随机性。若在非线性动态概率分析时随机变量选取比稳态概率分析复杂得多。例如以下2个非线性变量之间存在一一对应关系

如果分析变量X对系统输出响应的影响，传统的做法是先分析各元素xi（i=1,2,…,k）对系统输出的影响，再对其进行综合分析判断。该方法需要对每个变量的元素进行考虑和计算，过程繁琐，效率低；另外，在对每个元素进行综合分析时，没有统一有效的规则，不能保证计算效果和精度。因此，为了选取变量方便，需要对变量进行处理变换。

首先，选取变量X中的元素最大值，记作xmax；X中所有变量均除以xmax，即

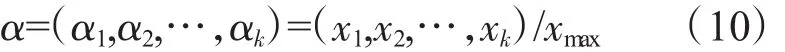
再用α和xmax表示X中的各元素，即

这样就把X中各元素之间的关系转换为X中各元素分别与最大值xmax的关系，在选取非线性或动态随机变量时，就可以用最大值xmax代替X中各元素来分析对输出响应影响，再根据X中各元素与xmax之间的相关性确定X中各元素对系统输出的影响。如果Y也表示成式（11）形式，那么X、Y各元素之间仍然存在一一对应关系。该方法在概率分析时减少了随机变量个数，能大大节约计算时间和提高计算效率与精度。在有限元分析中，在相邻元素间的分析点可以通过式（12）插值方法来处理。假设已知X、Y2个随机变量相邻2点xi,xi+1和yi,yi+1，并且存在一一对应关系，则[yi,yi+1]中的任何一点yik相对应的xik为

在选取机匣模型的随机变量时，材料非线性和温度载荷动态性都按以上方法选择其最大值进行概率分析，选择的随机变量及其抽样统计特征见表1，表中参数均服从正态分布，且相互独立。

表1 机匣随机变量及其数字特征

2.3 确定性分析

利用表（1）中各变量的均值，对机匣径向变形进行确定性分析，可得径向变形量随时间变化规律，如图5（a）所示，其中在t=180 s时变形量达到最大0.87 mm，此时机匣径向变形如图5（b）所示。

图5 机匣径向变形量规律及在t=180 s时变形

3 机匣径向变形的动态概率分析

3.1 动态概率分析

将随机变量的统计特征和边界条件导入有限元模型中，利用Box-behnken矩阵抽样法得到41组样本点，其中输出响应Y的样本历史如图6（a）所示。再利用这些样本点值拟合极值响应面函数式（3）（忽略小于10-7的系数），得到

建立极值响应面后，不但可得输出参数与各随机输入变量之间的关系，也可以得到与某2个随机变量的函数关系，比如输出参量Y与对流系数ac和燃气温度tc之间的关系，如图6（b）所示。

将极值响应面函数代替机匣有限元模型，利用MC法进行1万次抽样，得到Y（X）模拟样本历史和频率分布，如图7所示。从图7和图8（e）中可见： 满足正态分布，其均值约为0.87 mm，标准差为0.033 mm。部分随机变量的概率分布如图8所示。从图8中可见，输入随机变量都满足正态分布。根据表1提供的参数，当置信区间为0.95，设计机匣径向变形量为0.95 mm时，根据式（8）可得可靠度R约为0.993。

图6 输出响应Y样本历史及输入输出关系

逆概率分析，即计算某可靠度下所需要的变量参数值。在置信水平为0.95下的部分可靠度相对应的随机变量极限值见表2。

图7 机匣径向变化量模拟结果

图8 各随机变量概率分布

表2 不同可靠度下随机变量极限值

3.2 灵敏度分析

灵敏度是用来分析随机输入变量的变化对输出参量稳定性的影响程度，从而决定哪些参数对可靠性失效影响较大。通过对机匣径向变形分析，得到各参量的灵敏度及其分布，见表3并如图9所示。

表3 随机变量的灵敏度

在条状图中，最重要的随机输入变量（灵敏度最大）在最左边，其他依次向右排列。从表3和图9中可见，燃气温度tc对机匣径向变形量的影响最大，起决定性作用，影响概率占97.24%，其他随机变量的影响很小，其结论几乎与实际试验相符。由此为机匣径向变形与高压涡轮叶尖径向间隙设计、优化和控制提供了依据，首先要考虑转速的影响，再考虑其他因素的影响。

3.3 有效性验证

为了验证ERSM的有效性和优越性，基于表1中的随机输入变量和统计特征及相同计算环境，分别用MCM和RSM对机匣径向变形进行动态概率分析，并比较计算结果。在计算过程中，3种方法都是1万次模拟计算，其中ERSM和RSM的抽样次数均为41。以MCM计算为基准，其对比结果见表4。

表4 3种方法概率分析结果比较

由表4中可见，本文提出的极值响应面法的计算精度几乎与MC法的相同，但计算时间远少于其他2种方法，约为MC法计算时间的1/220、传统响应面法的1/3。可见，ERSM既能保证计算精度，又可大大缩短计算时间和提高计算效率。

4 结论

（1）介绍了极值响应面法（ERSM）的基本原理，建立了其数学模型，以涡轮机匣径向变形的动态概率分析为例，加以验证。该方法能在保持计算精度的前提下，大大节约计算时间和提高计算效率，充分验证了该方法在结构动态概率分析中的可行性和有效性。

（2）如何利用该方法进行机匣径向变形设计和优化，还需进一步探索和研究。另外，对于复杂结构（比如航空发动机高压涡轮叶尖径向间隙）动态概率分析，采用该方法是否仍能保证高效率需要进一步验证。

[1]NASA Glenn Research Center.HPT clearance control[R].NASA-CR-2005-213970.

[2]Lattime S,Steinetz B.Turbine engine clearance control systems:current practices and future directions[R].AIAA-2002-3790.

[3]杜小琴,朱惠人,张宗卫，等.涡轮机匣壁面换热特性的数值计算[J].航空工程进展,2010,1（4）：384-389.

[4]Pietrzyk k,Hagentoft C E.Probabilistic analysis of air in fi ltration in low-rise buildingsl[J]. Building and Environment,2008,43（4）：537-549.

[5]刘志全.航天器机械可靠性特征量裕度的概率设计方法[J].中国空间科学技术，2007（4）：34-43.

[6]Lü Q,Low B K.Probabilistic analysis of underground rock excavations using response surface method and SORM[J].Computers and Geotechnics,2011,38（8）：1008-1021.

[7]张春宜,白广忱,向敬忠.基于极值响应面法的柔性机构可靠性优化设计 [J].哈尔滨工程大学学报，2010,31（11）：1503-1508.

[8]李昌,韩兴.基于响应面法齿轮啮合传动可靠性灵敏度分析[J].航空动力学报，2011,26（3）：711-715.

[9]费成巍，白广忱.航空发动机涡轮叶片径向变形的概率分析[J].航空发动机，2012，38（1）：17-20.

[10]Kartal M E,Basaga H B,Bayraktar A.Probabilistic nonlinear analysis of CFR dams by MCS using response surface method[J]. Applied Mathematical Modelling, 2011, 35 （6）:2752-2770.

[11]Mollon G,Dias D,Soubra A H.Probabilistic analysis of pressurized tunnels against face stability using collocation based stochastic response surface method[J].Journal of Geotechnical&Geoenvironmental Engineering,2011,137（4）:385-397.