用变量代换法求解一类非齐次热传导方程Cauchy问题①

陈敏江， 赵书银， 贾丽萍， 于 坤

(1.石家庄经济学院数理学院，河北 石家庄 050031;2.河北建筑工程学院数理系，河北 张家口 075024;3.中核第四研究设计工程有限公司，河北 石家庄 050021)

0 引言

数学物理方程问题不仅形式变化多样，而且涉及了较深的数学内容，故其求解比较困难.另外，在本学科中，处理问题的方法具有很强的针对性，若方程的形式或条件做稍许修改，求解问题的思路及方法可能相差甚远.虽然部分定解问题有现成的求解公式，但其中有些项的计算非常复杂，不易记忆.

考虑如下热传导方程的Cauchy问题

其中f(x，t)∈C2，1(R ×[0，+ ∞))，φ(x)∈C(R)∩ L∞(R).

由傅氏变换，可得Cauchy问题(1)的解

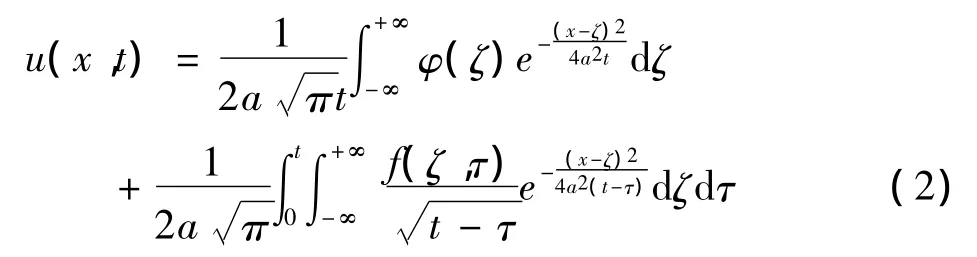
很显然，公式(2)的形式复杂，不易记忆，况且带有含参量的二重积分计算极易出错.

本文将指出，当非齐次项具有如下形式

时，我们通过变量代换法可将问题(1)中方程齐次化，再由泊松公式求出其解.这样做的最大优点避免了公式(2)的繁杂计算，而且求解过程简单明了、易于接受.

1 主要结果

考虑如下热传导方程Cauchy问题

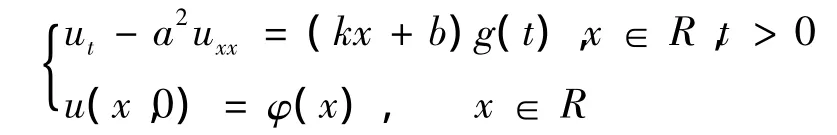
其中函数g(t)∈C1([0，+∞))，φ(x)∈C(R)∩L∞(R)均已知，k，b为常数.

我们希望找到一个具有如下形式的函数v(x，t)=(k1x+b1)g1(t)，通过变量代换，得

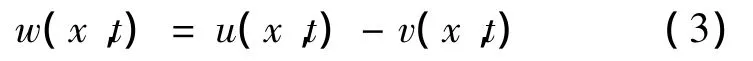
再适当地选择 k1，b1，g1(t)，将定解问题中的非齐次方程转化为关于w(x，t)的齐次方程.

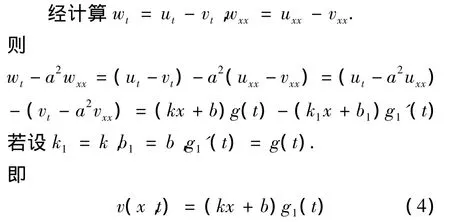
注:在上述表达式中，g1(t)=∫g(t)d t只需取不带常数的g(t)的原函数[3].

则Cauchy问题(1)中的非齐次方程经变量代换转化成齐次方程，即有如下形式

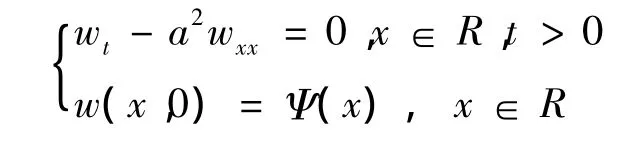
其中

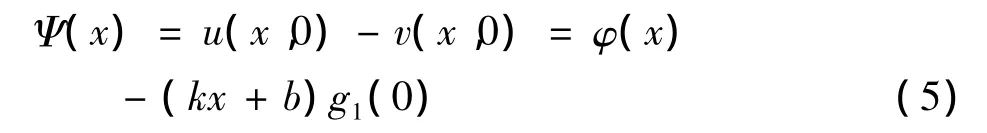
由热传导方程的泊松公式可得

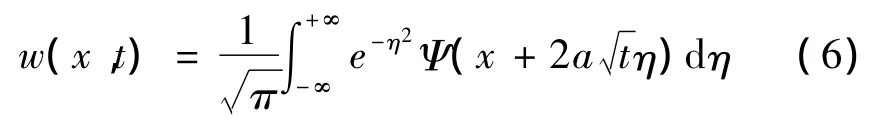
结合(3)，(4)，(6)可求得Cauchy问题(1)的解

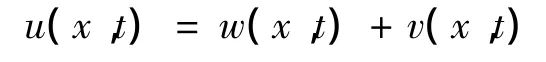
2 举 例

例1 求解下列热传导方程Cauchy问题

变量代换，w(x，t)=u(x，t)－ v(x，t).

由(5)得Ψ(x)=φ(x)－(kx+b)g1(0)=x－0=x，

得到关于w(x，t)的齐次Cauchy问题

由热传导方程的泊松公式可得

其中 k=1，b=0，g(t)=et

由公式(4)，可得k1=k=1，b1=b=0，g1(t)=∫etd t=et

即 v(x，t)=(k1x+b1)g1(t)=xet.变量代换，w(x，t)=u(x，t)－ v(x，t).

由(5)得

得到关于w(x，t)的齐次Cauchy问题

由热传导方程的泊松公式可得

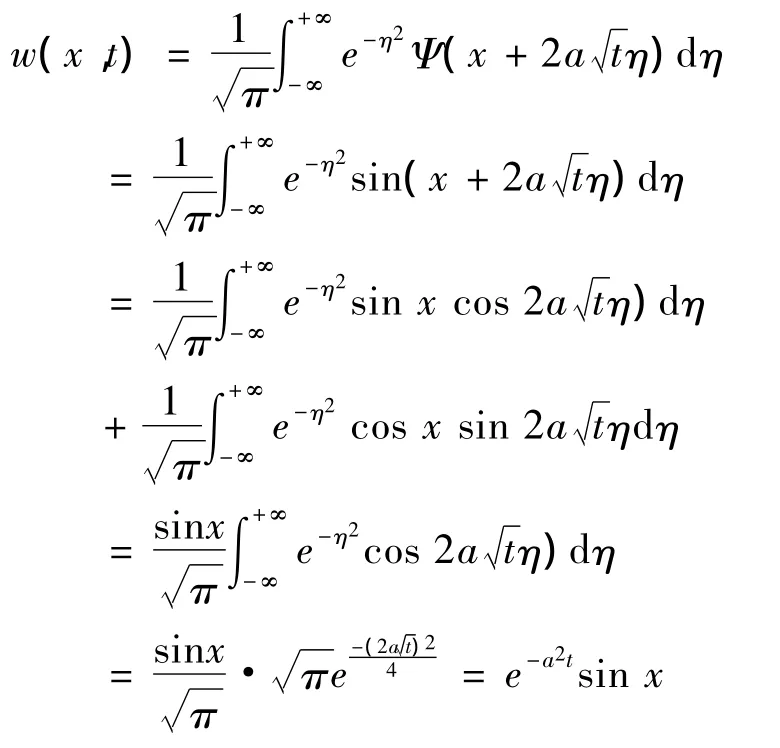
故原方程的解为

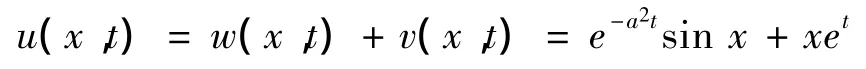
3 结 论

1)本文所给出的方法较之传统的傅氏变换方法，一则计算量小，二则简单明了、易于接受.

2)在Cauchy问题(1)中，当非齐次项具有形式f(x，t)=(kt+b)g(x)时，用变量代换法完全可以求解.

3)本文所提出的思想可应用于波动方程、Laplace方程的类似问题.

[1]姜礼尚，陈亚浙，刘西恒，等.数学物理方程讲义[M].北京:高等教育出版社，1996.

[2]王元明.数学物理方程与特殊函数[M].北京:高等教育出版社，2004.

[3]张东.变量代换法在求解微分方程问题中的应用[J].辽宁交通高等专科学校学报，2003.

[4]Lawrence C.Evans，Partial Differential Equation[M].American Mathematical Society，1998.