多点吊耳排气尾管的解耦分析①
吴孟乔, 周 鋐
(同济大学新能源汽车工程中心,上海 201804)
0 引言
在现代汽车的设计开发与宣传销售过程中,车内噪声与振动水平,作为NVH的重要指标已经成为评价车辆优劣的关键因素.车内的噪声和振动是由多个激励源通过不同的传递路径抵达目标位置后经过矢量叠加而成的.为了能够更好地优化整车的NVH性能并且研究激励源和传递路径的特性,传递路径分析(TPA)是一种十分直接有效方法[1].通过传递路径分析可以找出对车内噪声与振动产生较大贡献的路径与激励源,通过控制和优化关键因素可以有效的改善噪声与振动水平.
本文研究的对象是某车型排气尾管,作为动力总成中贡献较大的振动源,往往会有多个位置以吊耳的形式与车身相连.在实际汽车行驶工况中,每一个吊耳的振动并非独立于其他的吊耳,在错综复杂的结构与布置形式下,如何能够在最快的时间和使用最少的设备下,取得较为满意的信号是研究吊耳之间解耦关系的重点所在.
1 TPA基本原理
图1所示,为整车系统包含多个激励源,多条路径和多点响应,构成了一个完整的TPA整车模型.
假设整车为一线性系统,则所有的输入源都可视作线性系统的输入,而每一条传递路径则可以用对应的传递函数来代替.结合线性系统的特性,可以得到模型目标点的总响应值:
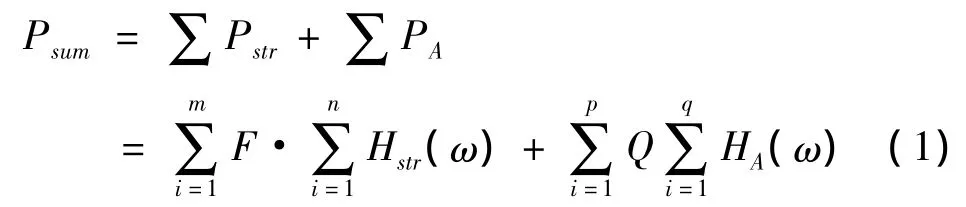
本文中仅涉及传递路径分析中由排气尾管吊耳振动引起的结构振动响应的传递特性,由式1推演可以得到下式:

式中:Fi,j(ω)为排气尾管第i个吊耳的j向激励;Hi,j(ω)为该路径到振动目标点的传递函数;Astr为结构振动的加速度信号.
2 逆矩阵求载荷法
在式2中,激励力Fi,j(ω)较难直接通过试验求得,可以利用逆矩阵法来间接求得激励力信号[3].
对于线性函数y=kx+b,只要给定自变量x,就可以求解出y.当k不等于零时,则可以求出其反函数x=(y-b)/k.根据反函数,只要知道任意函数值y,则可以求解自变量x.逆矩阵法的原理类似于通过反函数来求解自变量.
对于某一振动的线性系统来说,当有激励力F1,F2,…,FN时,存在响应值 X1,X2,…,XM,由系统的运动方程可得:

因此耦合激励可以用下式来估计载荷:
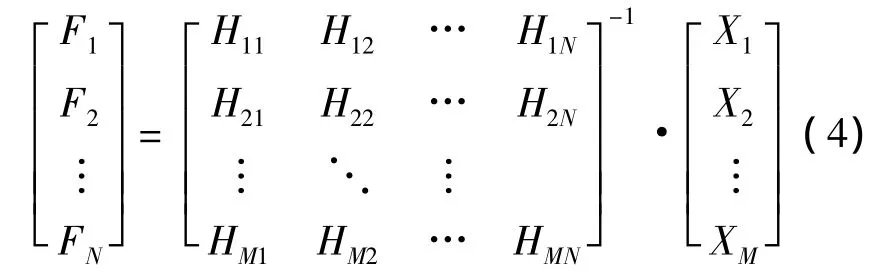
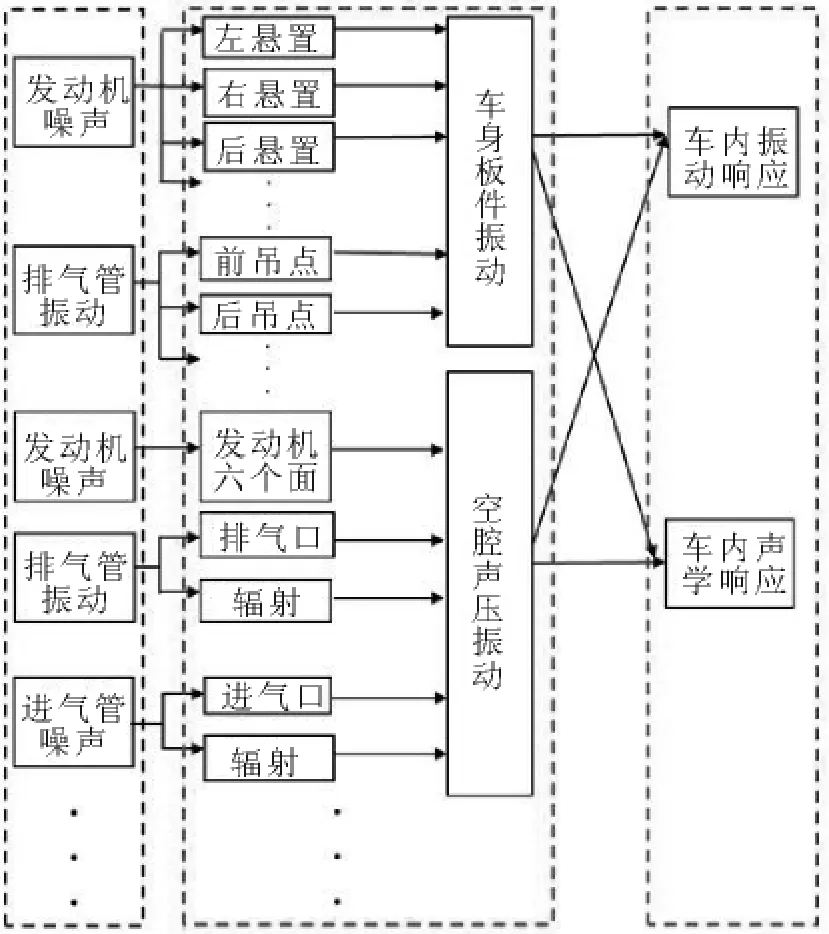
图1 整车系统传递路径分析示意图
上式可简写为:

式中:{F(ω)}为耦合激励力向量;{X(ω)}为耦合响应向量,称之为参考自由度;Hij=Hi/Fj为由输入Fj到响应Xi的频率响应函数(传递函数).由于响应的形式多种多样,因此频率响应函数也分为力—位移,力—速度,力—加速度三种.
经由式5,把激励力的求解问题演化成为了数值的矩阵求解问题.为了抑制噪声,避免数值问题,并使估计出的耦合激励力更为精确,应使参考自由度数M不小于耦合激励力数N(传递路径数).通常取M≥2N.当 M > N 时,并不存在,以=([H]T[H])-1[H]T来代替.同时,为了避免因[H]可能是病态矩阵而引起的计算错误,需要对[H]进行奇异值分解.

图2 吊耳布置图

图3 第一吊耳Z向激励力的四种耦合关系对比图

图4 排气尾管吊耳激励引起的方向盘Z向振动加速度对比图

图5 第2,3个吊耳激励到第1个吊耳参考自由度的传递函数
3 多点吊耳排气尾管的建模
试验所用试验车为某型号的SUV,由于开发设计上的要求,前后共有5个吊耳与车身相联接,吊耳描述及布置形式参考下图2.
在试验中,选取了多种常用汽车行驶工况,如怠速,多级定速巡航,多档位全油门半油门加速等,并且采集了关心位置上的振动加速度响应以及噪声声压响应,如驾驶员右耳振动,驾驶员地板振动等.
同时,在使用逆矩阵法求载荷时应注意:参考自由度须取在被动方,本次试验中指承载式车身;尽量分布在耦合点附近,一般选取十厘米左右;在测量频响函数HM×N时,主动方应在各耦合点处与被动方解耦并从耦合点移走,以消除激励源耦合的影响*,即在试验中拆除动力总成进行试验;有时需要根据耦合点处的结构形式制作相应的连接件,用于力锤敲击,安装加速度传感器或者激振器等.由于吊耳的结构相对简单,直接用力锤敲击耦合点.
根据试验车实际情况,进行以下合理的简化:忽略噪声源对结构振动的影响,发动机悬置与排气尾管吊耳之间的耦合关系[4].
为了便于说明,选取方向盘z向振动作为目标信号,考虑到y,z两个方向上平动自由度相对于x向的平动自由度对车内振动贡献较大,因此排气尾管的振动共通过2×5=10条路径传递到方向盘处.则由排气尾管振动引起的方向盘z向振动的函数方程可用下式表示:

式中:Fij是第i个吊耳在第j个方向上的激励力,单位为N;Hij是第i个吊耳在第j个方向上的激励传递到驾驶员座椅地板的振—振传递函数,单位为N/N.
4 解耦分类讨论
在逆矩阵法求载荷力中,为了保证逆矩阵的精度,需满足矩阵超静定M≥2N的条件,我们在每个激励力产生的路径附近布置两个加速度参考自由度[5].通过力锤敲击激励点,可测得加速度参考自由度的加速度信号和与力锤的力信号之间的传递函数.试验车布置有五个吊耳,考虑y,z两个方向共10个激励力和20个加速度参考自由度,其关系如下式所示:

式中,Fij代表第 i个(i取1,2,3,4,5)吊耳在第 j个方向上(j取y、z方向)的激励力,单位为N;amnk代表第m个参考自由度(m取1,2)在第n个吊耳上(n取1,2,3,4,5)的第k个方向(k取y、z方向)上的加速度响应,单位为m/s2;Hij,mnk代表激励力Fij到加速度响应amnk的传递函数.
在实际试验操作中,通过对传递函数矩阵不同的数据选取方式,以及在试验中不同的数据采集方法,可以演变出不同的解耦方式,下面对四种不同的耦合方式加以讨论和评价.
4.1 全耦合
所谓全耦合,在本文中指,排气尾管的五个吊耳两两之间相互影响,关心的两个方向之间也互相关联,式7即表示全耦合的情况,其中传递函数矩阵中没有一个元素为零,全耦合能最完整的复现实车实际工况下的真实激励力,对最后的路径贡献分析也最准确,但是对试验设备的要求较高,需要一次性测量多个点,若分批次完成,则会大大增加试验的工作量.
4.2 近点耦合
近点耦合,指单个排气尾管吊耳(y、z方向)只与相邻的吊耳(y、z方向)之间相互关联耦合,忽略相对距离超过一个吊耳的其他吊耳对其的关联影响.即以 1,2;1,2,3;2,3,4;3,4,5;4,5 的组合进行试验.式7可改写成下式:
近点解耦考虑相近吊耳之间的相互影响,排除相隔较远吊耳的影响,可以减轻试验的工作量并且对降低对试验设备数量的要求.
4.3 坐标解耦
坐标解耦,指的是两个方向上激励力的分解,即y向与z向的解耦,说明在y向上的激励不会同时引起z向上的响应,或者z向上的激励不会引起y向上的响应.根据坐标解耦的定义,式7可改写为:

坐标解耦的方法认为空间三坐标上的力两两之间没有关联或者影响,可以简化试验思路,也可较为便利地开展试验.
4.4 全解耦
所谓全解耦,指吊耳相互之间没有影响,且所关心的两个方向也不相互关联.即在传递函数矩阵中只有吊耳单方向路径对同点同方向的参考自由度有传递函数参与计算.据此,式7可改写为:

5 载荷与贡献分析
根据上节所介绍的四种解耦方法,可以得到各路径的激励力和到目标点的传递函数,并且合成得到目标点的响应.
图3表示通过上节所述不同的解耦方法计算得到的第一个吊耳z方向上的激励力,从图中可以清晰的看出,近点耦合与全耦合所得到的激励力有相当高的重合度,并且在关键峰值处,如15Hz,27Hz,54Hz等,有相一致的幅值.采用坐标耦合的方法得到的激励力,在中高频段与全耦合的方法有一定的吻合,但是在低频段的吻合度不是很理想,有一定的误差,数据的可靠性受到了影响.最后采用全解耦的方法所得到的激励力已完全失真,幅值远大于全耦合所得到的激励力,说明虽然在理论讨论中具有可行性,但是不具备作为实际试验手段方法的可行性.
图4表示排气尾管激励通过10条路径,最后叠加到方向盘z向产生的加速度的响应,由于各路径到响应点的传递函数不受解耦方式的影响,所以目标点的响应也能较为直观的反应激励力的情况.从响应加速度信号分析,同样可以看出近点耦合所合成的响应与全耦合具有高度的一致性,且在27Hz的峰值频率上具有几乎相同的幅值,坐标解耦虽然在整体上与全耦合趋势相同,但是在关键频率27Hz上与全耦合的幅值相差很大.而全解耦则完全偏离真实指,在部分频段甚至超出一个数量级.
从上述分析中,可以了解到,采用近点耦合的解耦方法比坐标解耦的方法更加接近真实值,即采用全耦合的方法.从图5中可以进一步说明近点耦合比坐标解耦的更具合理性.
图5表示第2,3个吊耳激励到第1个吊耳参考自由度的传递函数,图中可以看出第2个吊耳激励到第1个吊耳异向参考自由度的2个传递函数在30Hz之前大于第3个吊耳激励到第1个吊耳同向参考自由度的2个传递函数.传递函数的幅值大小反映着传递率的大小,说明近点吊耳异向之间的传递关系大于远点吊耳同向之间的传递关系,进一步得到近点吊耳异向之间的耦合关系大于远点吊耳同向之间的耦合关系.从图5也可以注意到近点耦合在30Hz之前比坐标解耦更接近全耦合的情况.由于坐标解耦忽视了其他吊耳,尤其是近点吊耳异向激励对其的影响而造成了一定的误差.相较坐标解耦,近点解耦在简化试验的前提下,较好地优化了排气尾管的TPA模型,忽略了距离较远吊耳对激励力的耦合小量影响,得到了比较好的结果.
6 总结
本文简要介绍了TPA的基本原理,以及结合试验车排气尾管具体布置形式的建模方式,并且提出了四种不同的解耦方法,分别计算了其激励力,并且进行了相互比较和具体分析.最后根据本次试验车排气尾管的特点:多吊耳和紧凑布置,得出了近点解耦要优于坐标解耦的结论.结合多点布置的具体情况,该思路可以拓展到其他多吊耳布置的排气尾管,多悬置布置的发动机,抑或多弹垫布置的客货车等非承载式车身上,提供了一定的参考价值.
[1]刘东明,项党,罗清等.传递路径分析技术在车内噪声与振动研究与分析中的应用[].噪声与振动控制,2007,4:73-77.
[2]梁映珍.基于传递路径分析的车内噪声研究[J].上海:同济大学,2010.
[3]靳晓雄,张立军.汽车噪声的预测与控制[D].上海:同济大学出版社,2004.
[4]麻海舰.轿车排气噪声声品质试验分析与优化研究[D].上海:同济大学,2008.
[5]庞剑,谌刚,何华.汽车噪声与振动——理论与应用[M].北京:北京理工大学出版社,2006.

