基于交互式多模型粒子滤波的相控阵雷达自适应采样

郁卫华 ， 朱 翔 ， 朱晓华

（1.南通农业职业技术学院 江苏 南通 226007；2.南京理工大学 电子工程与光电技术学院，江苏 南京 210094；3.国网电力科学研究院 江苏 南京 210003）

基于交互式多模型粒子滤波的相控阵雷达自适应采样

郁卫华1，2， 朱 翔3， 朱晓华2

（1.南通农业职业技术学院 江苏 南通 226007；2.南京理工大学 电子工程与光电技术学院，江苏 南京 210094；3.国网电力科学研究院 江苏 南京 210003）

为有效合理利用雷达资源和解决雷达测量值与运动状态间的非线性关系以及目标状态本身可能出现的非线性，提出了一种基于交互式多模型粒子滤波（IMMPF）的相控阵雷达自适应采样目标跟踪方法。将交互式多模型粒子滤波一步预测值的后验克拉美罗矩阵代替预测协方差矩阵，通过该矩阵的迹与某一门限值比较来更新采样周期以适应目标运动状态的变化。将该方法与基于量测转换的IMM自适应采样算法进行仿真实验，表明了该算法的有效性。

相控阵雷达；交互式多模型；粒子滤波；后验克拉美罗矩阵（PCRB）；自适应采样

相控阵雷达采用电子扫描的方式使得天线波束指向无惯性的捷变，实现了雷达跟踪目标时可根据目标运动状态自适应地改变采样周期[1]。当目标机动时，采用高采样率，实现对目标进行更精确跟踪，以避免跟踪丢失。反之，当目标处于平稳状态时，在一定跟踪误差内，采用一个相对低的采样率。这种依据目标运动状态自适应改变采样周期的手段可在保证基本跟踪误差的前提下，更合理有效地利用雷达资源，充分发挥相控阵雷达的多目标跟踪能力[2]。

Bar-Shalom提出的交互式多模型（IMM）算法是目前机动目标跟踪中最有效的算法之一。但由于雷达测量值与目标运动状态间的高度非线性关系以及目标状态本身可能出现的非线性，使得卡尔曼滤波或扩展卡尔曼滤波算法性能大大下降。Gordon提出的粒子滤波（PF）作为一种基于贝叶斯估计的非线性滤波算法，在处理非高斯非线性时变系统的参数估计和状态滤波问题方面有独到的优势。融合IMM和PF的新滤波方法，即交互式多模型粒子滤波器（IMMPF），可同时解决雷达测量值与运动状态间的非线性关系和目标机动运动带来的跟踪困难，因此该方法的滤波性能要远远优于传统的IMM方法。

文中基于交互式多模型粒子滤波（IMMPF）的目标跟踪算法，提出将交互式多模型粒子滤波一步预测值的后验克拉美罗矩阵（PCRB）代替预测协方差，选取该矩阵的迹不超过某一门限值的最大采样间隔作为下一时刻的采样间隔，使得雷达在满足要求的跟踪误差情况下，实现雷达资源的有效利用。文章首先分析了IMMPF算法，接着给出了IMMPF的PCRB迭代更新方法，然后提出基于IMMPF的自适应采样算法，最后进行了计算机仿真实验。

1 交互式多模型粒子滤波

1.1 粒子滤波

粒子滤波算法（PF）是一种基于蒙特卡洛仿真的近似贝叶斯滤波算法[3]，其核心思想是使用一组具有相应加权值的随机样本（粒子）来表示后验概率密度（PDF）[4-5]。它首先在状态空间中根据先验分布产生一组粒子，然后在观测的基础上通过调节每个粒子所对应权值的大小和位置，来获得服从实际分布的粒子，并以该组粒子的均值作为系统状态估计值，最后对这组粒子权重采样以保证权重的均匀分布。

目标跟踪问题可以描述为在给定一组观测的条件下对系统的状态进行估计。在随机系统离散的形式下，目标运动的状态方程可表述为：

其中xk为状态向量，vk为与状态无关的过程噪声，fk表示系统状态转移模型。

相控阵雷达系统的测量方程可表述为：

其中nk表示独立于系统测量的热噪声，hk表示系统测量模型。

设已知系统状态的初始概率密度函数为 p（x0|z0）=p（x0），则状态预测方程为：

状态更新方程为：

其中，

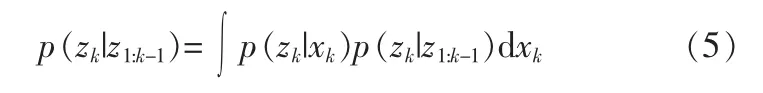
递推求解式（3）、（4）可得到贝叶斯最优估计，但在实际系统中，很难求出PDF。基于随机采样运算的蒙特卡罗方法可将积分运算转化为有限样本点的求和运算，可以解决上述问题。如果能从PDF上随机抽取一组粒子来逼近，则PDF可用这组粒子来逼近。通常很难直接从PDF上抽样粒子，但可从一已知的分布上随机抽取一组粒子来逼近PDF。

若将重要密度函数q（x0:k|z1:k）可以写成如下递推形式：

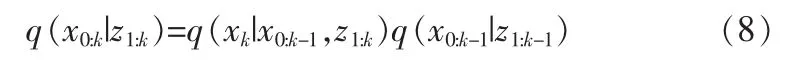
把公式（4）、（5）、（8）代入到公式（7）中，于是权值的递推形式可表示为：

预测、更新和权值估计就构成了基本的序贯重要抽样（SIS）法，这是粒子滤波算法的基本框架[6]。粒子滤波依靠重要抽样，因而要求重要密度分布尽可能地逼近PDF。

1.2 交互式多模型粒子滤波算法

1）随机抽取粒子

2）输入交互

3）模型匹配粒子滤波

4）模型概率更新

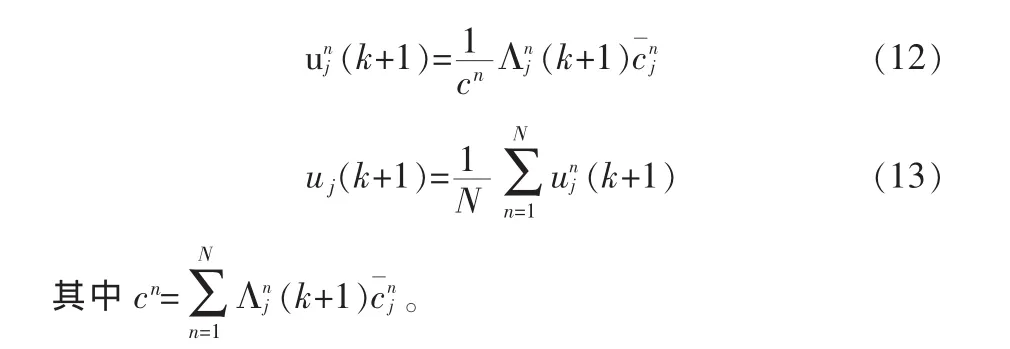
5）残差重抽样

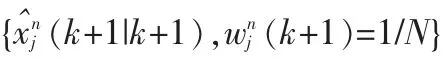
6）输出交互

对m个模型的各相应的粒子群进行输出交互，然后对所有的粒子求加权平均和：

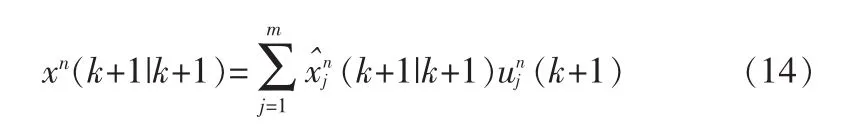
2 基于IMMPF的自适应采样

根据IMMPF算法可以看出，粒子滤波过程中并不能直接求出预测协方差矩阵，因此无法建立预测协方差矩阵与采样间隔的关系，导致无法直接利用IMMPF进行自适应采样。在参数估计理论中，对任何无偏估计量的方差存在一个下限。尽管存在许多这样的限，但克拉美罗下限是最容易确定且最有效的一种。文献[8]中给出了非线性滤波下后验克拉美罗界（PCRB）及其迭代更新公式，因此将预测值代入PCRB中就可以得到该预测值的估计质量。将预测协方差矩阵用预测值的PCRB矩阵来替代，通过建立该矩阵与采样间隔的关系，就可以实现基于IMMPF的自适应采样。

2.1 交互式多模型粒子滤波下的后验克拉美罗界（PCRB）

假设在k时刻考虑目标跟踪问题，根据上述IMMPF滤波算法通过雷达测量值z1:k来估计目标轨迹x0:k，那么目标轨迹的贝叶斯信息矩阵（Bayesian Information Matrix BIM，其逆矩阵为PCRB）可以表示为：

根据文献[8]中PCRB更新迭代公式，单模型下更新k+1时刻的BIM为的递推公式为：

其中Q为过程噪声协方差矩阵，F为系统状态转移矩阵，Γk+1为测量误差所引起的协方差矩阵。因此交互式多模型下更新k+1时刻的Jk+1的递推公式表示为

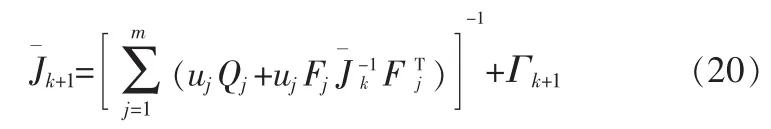
其中uj为模型j的模型更新概率，Qj为模型j的过程噪声协方差矩阵，Fj为模型j的线性系统状态转移矩阵或非线性状态转移矩阵的一阶导数。当采样周期变化时，则Fj也随之变化，从而Jk+1变化。Γk+1为雷达测量误差所引起的协方差矩阵，其定义为

由式（20）、（21）可知，目标轨迹的 PCRB矩阵与状态模型和观测模型都相关的，通过后者可以算出Γk+1。但由于模型采用粒子滤波时，则需要计算每一粒子的Γk+1，计算量很大。根据文献[9]，Γk+1可表示为

其中Ξk+1是由测量值zk+1来估计状态值xk+1的标准的费舍信息矩阵（Fisher Information Matrix，FIM）。在自适应采样过程中，由于zk+1在k时刻是未知的，因此采用预测值代替量测值来计算。

2.2 自适应采样原则

目标状态预测误差能很大程度上反映目标跟踪的情况，因此常用预测协方差门限法来实现雷达系统的自适应采样控制。本文依据该思想，用下一时刻预测PCRB矩阵的迹与给定门限值比较，选择最佳下一时刻雷达采样间隔。

具体算法是，当计算得到的下一时刻预测PCRB矩阵的迹小于给定的门限值时，则雷达的采样间隔增加一个步进，直到PCRB矩阵的迹超过门限值时，则此时雷达的采样间隔的前一步进即为最终输出的下一个时刻的雷达采样间隔。反之，当计算得到的下一时刻预测PCRB的迹超过给定的门限值时，则雷达采样间隔减少一个步进，直到预测PCRB的迹小于门限值时，同样此时雷达的采样间隔的前一步进为最终输出的下一个时刻的雷达采样间隔。

假设当前时刻为k，采样间隔为Tk，门限值为Pth算法可表示如下：

这样，对于稳定跟踪的目标，目标跟踪精度较高，则采样间隔可以增大，有效地节约了雷达资源。当目标处于机动状态时，雷达的跟踪精度下降，迫使目标状态的预测PCRB矩阵增大，超过门限值，则采样间隔相应减小以提高雷达跟踪精度。

3 仿真实验与结果分析

为了验证基于IMMPF的相控阵雷达自适应采样方法的有效，本文选取典型的目标机动环境进行仿真，并将仿真结果与基于量测转换的IMM自适应采样方法[10]进行比较。假定目标运动在X-Y平面内运动120 s，高度保持不变，起始位置（2 500 m，8 000 m）。在t=0 s开始以100 m/s沿X轴匀速运动，在t=21 s时以1.5 g加速度机动转弯，在t=36 s时匀加速运动，在t=66 s时又恢复匀速运动。目标整个过程的运动轨迹如图1所示。仿真过程中假设相控阵雷达的测距误差Pr=100 m，测角误差 ρθ=0.03 rad。 自适应采样间隔为 0.8 s、1.0 s、1.2 s、1.4 s、1.6 s、1.8 s和2.0 s。采用匀速、匀加速和常速率转弯3种模型，模型先验概率 Mo=[1/3，1/3，1/3]，Markov模型转移概率

图1 目标的运动轨迹Fig.1 The trajectory of target

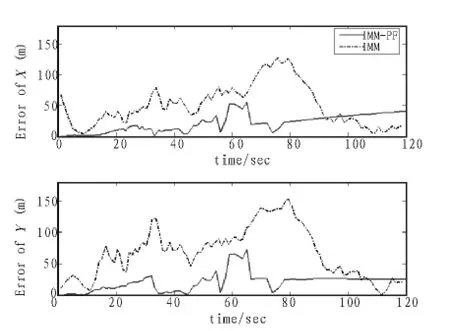
图2 平均更新时间1.2 s下IMMPF和IMM算法X轴和Y轴跟踪误差Fig.2 Tracking error of X-axis and Y-axis using IMMPF and IMM algorithm on average update time 1.2 s

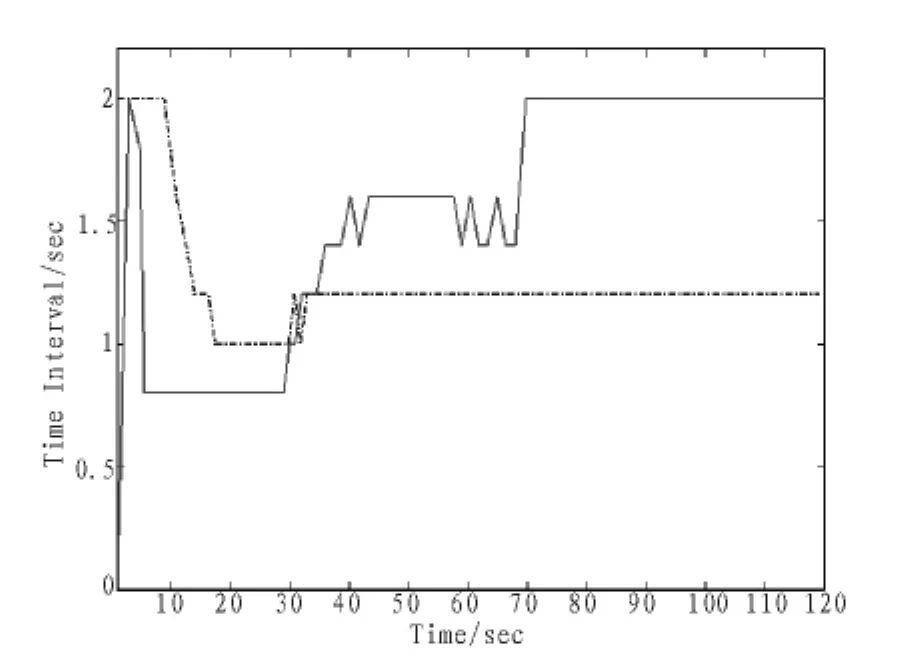
图3 相同门限下IMMPF和IMM的更新时间Fig.3 Time interval using IMMPF and IMM algorithm on the same threshold

平均更新时间1.2 s下IMMPF和IMM算法X轴和Y轴跟踪误差如图2所示。由图可见，IMMPF算法的跟踪误差要明显小于基于量测转换的IMM算法。在初始非机动时间段，由于PF比量测转换在非线性量测方程下具有更好的性能，因此IMMPF在初始阶段的跟踪误差就小于IMM。当目标突然开始机动时，由于IMMPF能从粒子群中选择能较好反映目标运动状态的粒子并进行复制，而且各模型间的粒子群还能存在交互，因而IMMPF可较快的适应机动，导致IMM跟踪误差与IMMPF相比进一步扩大。

相同门限下IMMPF和IMM算法的更新时间如图3所示。由于IMMPF本身的跟踪性能很好，在目标机动段通过减小更新时间来保持跟踪质量，在非机动段增大更新时间。而IMM由于其跟踪性能有限，在非机动段无法增大更新时间，限制了其自适应采样的性能。在整个时间段中，IMMPF的平均更新时间为1.38 s，IMM的平均更新时间1.2 s。在相同时间内，IMMPF所需的采样次数比IMM要少15%，因而IMMPF具有比IMM更好的自适应采样性能。

4 结 论

雷达采样间隔时间，对相控阵雷达多目标跟踪性能影响很大，因此自适应的采样间隔不仅合理有效地利用了雷达资源，同时对确保跟踪的连续性，可靠性和跟踪精度有重要意义。本文提出的基于IMMPF的自适应采样算法能有效地根据目标运动状态自适应更新采样间隔，使得系统在目标处于非机动的稳定状态时用较大的采样间隔，而在目标处于机动状态时采用较小的采样间隔，以确保目标跟踪不丢失。

[1]张光义，赵玉洁.相控阵雷达技术[M].北京，电子工业出版社，2006.

[2]王峰，张洪才，潘泉.相控阵雷达采样周期自适应策略研究[J].系统仿真学报，2003，15（9）:1230-1233.

WANG Feng，ZHANG Hong-cai，PAN Quan.A study on adaptive sampling period of phased array radar[J].Acta Simulata Systematica Sinica，2003，15（9）:1230-1233.

[3]王鑫，胡昌华，暴飞虎.基于贝叶斯原理的粒子滤波算法[J].弹箭与制导学报，2006，26（2）:269-271.

WANG Xin，HU Chang-hua，BAO Fei-hu.Particle filtering method based on Bayesian theorem[J].Journal of Projectiles，Rockets，Missiles and Guidance，2006，26（2）:269-271.

[4]Arulampalam S，Maskell S，Gordon N，et al.A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking[J].IEEE Trans.on Signal Processing，2002，50（2）:174-188.

[5]杨德贵，张长城，郑涛.粒子滤波算法的性能分析与改进[J].电光与控制，2008，15（5）:72-75.

YANG De-gui，ZHANG Chang-cheng，ZHENG Tao.Performance analysis and improvement of particle filter algorithm[J].Electronics Optics&Control，2008，15（5）:72-75.

[6]张琪，胡昌华，乔玉坤.基于权值选择的粒子滤波算法研究[J].控制与决策，2008，23（1）:117-120.

ZHANG Qi，HU Chang-hua，QIAO Yu-kun.Particle filter algorithm based on weight selected[J].Control and Decision，2008，23（1）:117-120.

[7]邓小龙，谢剑英，杨煜普.基于交互式多模型的粒子滤波算法[J].系统仿真学，2005，17（10）:2360-2380.

DENG Xiao-long，XIE Jian-ying，YANG Yu-pu.Particle filter based on interacting multiple model[J].Acta Simulata Systematica Sinica，2005，17（10）:2360-2380.

[8]Tichavsky P，Muravchik C H，Nehorai A.Posterior cramerrao bounds for discrete-time nonlinear filtering[J].IEEE Trans.on Signal Processing，1998，46（5）:1386-1395.

[9]Hurtado M，Nehorai A.Adaptive path design of a moving radar[M].Sensor， Signal and Information Processing Workshop，2008.

[10]周文辉.相控阵雷达及组网跟踪系统资源管理技术研究[D].长沙：国防科技大学，2004.

Adaptive sampling method for phased array radar based on interacting multiple model particle filter

YU Wei-hua1，2， ZHU Xiang3， ZHU Xiao-hua2
（1.Nantong Agricultural Vocational Technology College，Nantong226007，China；2.School of Electronic Engineering and Optoelectronic Technology，Nanjing University of Science and Technology，Nanjing210094，China；3.State Grid Electric Power Research Institute，Nanjing210003，China）

In order to effectively utilize the resources of radar and solve the nonlinear relationship between radar measurement and target motion state，an adaptive sample target tracking algorithm for phased array radar based on interacting multiple model particle filter （IMMPF） is proposed.This algorithm first predicts Posterior Cramer-Rao Bound （PCRB） matrix of the target state，then updates the sample interval adapted to changing target dynamics by comparing the trace of the predicted PCRB with a certain threshold.Performances of constant and adaptive data rates are compared.Simulation results demonstrate the effectiveness of this algorithm.

phased array radar； interacting multiple model； particle filter； PCRB； adaptive sampling

TN958

A

1674－6236（2012）05-0029-04

2011-12-01稿件编号：201111148

郁卫华（1966—），女，江苏南通人，副教授。研究方向：雷达信号处理及应用电子技术教学。