基于地貌指数的汶川地震灾区单沟泥石流总量计算方法*

张怀珍，范建容

(1.中国科学院山地灾害与地表过程重点实验室，四川成都610041;2．中国科学院·水利部成都山地灾害与环境研究所，四川成都610041;3.中国科学院研究生院，北京100049)

基于地貌指数的汶川地震灾区单沟泥石流总量计算方法*

张怀珍1，2，3，范建容1，2

(1.中国科学院山地灾害与地表过程重点实验室，四川成都610041;2．中国科学院·水利部成都山地灾害与环境研究所，四川成都610041;3.中国科学院研究生院，北京100049)

现行的泥石流总量计算方法普遍存在计算参数较难获取或难以精确获取的问题，加上汶川地震灾区沟谷内分布大量的由崩塌、滑坡体等形成的固体松散物质;所以多数泥石流总量计算公式在汶川震区存在局限性。参考适用于以崩塌、滑坡体为主要物源的泥石流总量计算公式;分析研究区范围内地形地貌发育状态与降雨因素及其地质条件之间的影响关系;将地貌指数(Strahler积分)应用于泥石流总量计算，尝试解决缺乏降雨数据情况下泥石流总量计算问题。根据“8.13”四川清平群发性泥石流数据初步回归分析得到适合于汶川震区的泥石流总量计算模型。

单沟泥石流总量;汶川地震灾区;地貌指数;降雨

泥石流的形成过程十分复杂，其受地质、地形地貌及降雨条件等因素影响。在泥石流研究中，泥石流总量(一次泥石流事件中泥沙流出量)的确定既是泥石流危险性评价的关键参数，也是整个泥石流学科研究的重点。泥石流总量也是泥石流危险区面积、堆积长度、堆积厚度、最大流量等参数计算过程的中间参数。泥石流总量受到地质、地形、土壤、土地利用方式及降雨等泥石流形成因素的影响［1］。目前，关于泥石流总量的研究很多，多为建立在水文计算、调查和统计分析基础上的间接确定方法和经验、半经验公式;如雨洪修正法、泥痕调查法和配方法等。但由于多数公式存在参数较难获取或难以精确获取的问题;加上不同区域泥石流沟谷的区域性差异，使得这些公式难以推广［1－3］。最近，Gartner，J.E.，Cannon，S.H. 等通过对美国西部受火烧扰动区域的泥石流进行分析，经回归统计分析建立了适合于受火烧影响区域的泥石流总量计算模型［2－3］。庄建琦、崔鹏等(2009)参考受火烧影响的区域中泥石流总量的计算公式，结合受地震影响严重的云南蒋家沟泥石流实测数据，建立了受地震影响以崩塌、滑坡体为主要物源的泥石流总量计算模型［4］。

汶川大地震在岷江干流及其支沟两岸山坡引发了大量崩塌、滑坡，形成大量的松散固体物质，这些松散固体物质为泥石流形成提供直接物源，使得泥石流活动性增强［5－7］。本研究参考适合于以崩塌、滑坡体为主要物源的泥石流总量计算公式，分析研究区范围内地貌指数与降雨因素及其地质条件之间的影响关系，将地形地貌定量指数(Strahler积分)引入汶川震区泥石流总量计算，为震区灾后重建的工程措施设计建设提供参考数据。

1 研究区概况

研究区位于汶川地震主灾区，主要包括沿龙门山断裂带区域的白龙江上游、岷江上游、青衣江上游及部分小流域，经纬度范围处于102.5°～106.5 °E，29.2°～34.4°N(图 1)。该区域主要位于四川西部山区，山高谷深，地质构造复杂，断裂发育，属于滑坡和泥石流等山地灾害多发区。强烈地震导致山地区域的地质环境更加脆弱，整个震区滑坡、泥石流活动更加频繁、危害更加严重［5－7］。

地震形成的大量崩塌、滑坡直接为泥石流活动提供了丰富的松散固体物质，且地震造成大量坡体失稳和岩体破坏;使这些泥石流沟在今后较长一段时间内处于活跃期，泥石流暴发规模和频率显著增加［5－6］。崔鹏等指出震后次生灾害将进入活跃期，崩塌、滑坡的活跃期可能持续5～10年，泥石流的活跃期将可能持续20年。在未来5～10年内，因滑坡、泥石流强烈活动，灾害链［崩塌、滑坡→(泥石流→)堰塞湖→溃决洪水或泥石流］表现比较突出;随着泥石流、滑坡活动强度降低，灾害链表现逐渐减弱，出现概率减小［5］。

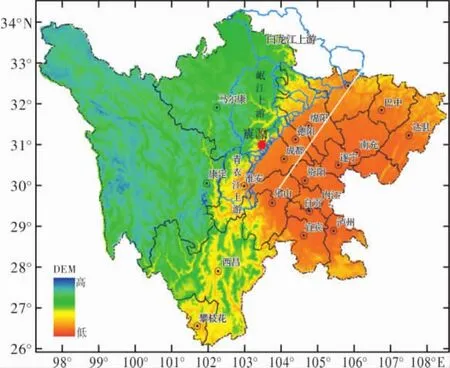
图1 研究区位置示意图

2 研究方法

目前，多数泥石流总量计算公式存在参数获取困难或参数缺乏准确性问题;而且现行的泥石流总量计算公式对于汶川地震形成的后发型地震泥石流存在一定的局限性。关于汶川震区泥石流总量计算的研究较少。庄建琦等参考受火烧影响区域的泥石流总量计算公式［2］:

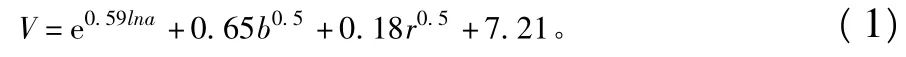
式中:V为泥石流总量(m3);a为坡度大于30%所占面积(km2);b为中度以上被火扰动的落地面积(km2);r为降雨量(mm)。结合云南蒋家沟实测泥石流数据得到受地震影响以崩塌、滑坡体为主要物源的泥石流总量V1计算公式［4］:

式中:V为泥石流总量(m);A为坡度大于30%所占面积;B为崩塌、滑坡体所占面积(km2);R为年最大日降雨量(mm)。这三个基本参数可理解为是对泥石流形成所需三个基本条件的描述参数:地形地貌条件(A)、物源补给条件(B)和降雨激发条件(R)。但在公式(2)中，R年最大日降雨量的获取较困难，给缺乏降雨数据情况下的泥石流总量计算带来一定的困难。

2.1 地貌发育状态与降雨因素之间的关系研究

降雨是重要的外营力作用之一，降雨因素在一定程度上影响地形地貌的发育。本研究从地形地貌发育条件出发，选择能够定量化描述地形地貌发育状态的地貌指数Strahler积分，研究其在所选研究区范围内与降雨因素的关系。Strahler积分是由美国地貌学家A.N.Strahler提出的面积－高程分析法计算获得，用来定量分析地貌发育阶段［8－9］。

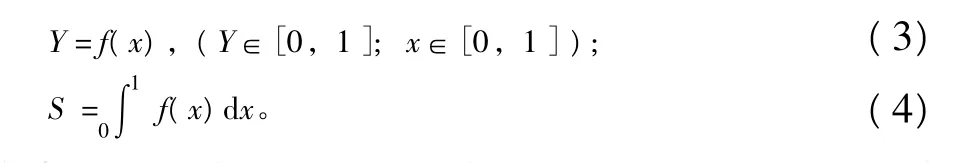
式中:Y=h/H，x=s/A;s，h分别为流域内某一点以上的流域面积和到流域最低点之间的高差;H，A分别为流域的最大高差和流域面积;S为斯特拉勒(Strahler)积分，其大小流域地貌发育有关，能够用来量化戴维斯模型的侵蚀流域地貌演化阶段［8－9］。

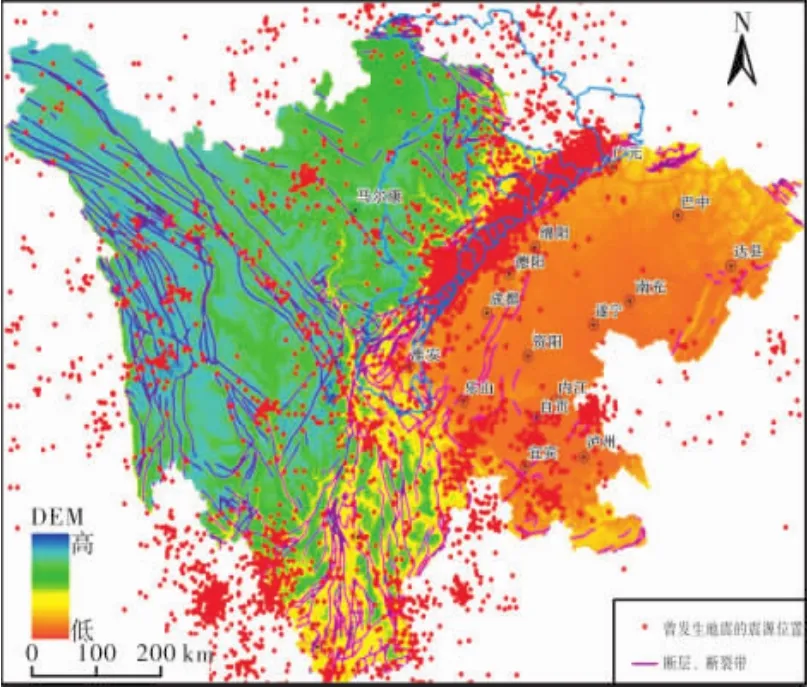
图2 研究区地质数据及地震数据

图3 研究区多年平均降雨量

研究区沿龙门山断裂带分布，地质构造复杂，断裂发育，地质活动(地震)频繁(图2)。整体上看，研究区是地震活动强烈和地震灾害严重的区域。即研究区范围内影响地貌发育的内营力作用分布差别不大。参考研究区多年平均降雨分布(图3)，研究区多年平均降雨量基本上从东南向西北方逐步减少。即研究区不同区域降雨量存在一定的差异。因此，在内营力差别不大的情况下，外营力(降雨)的差别将会是影响研究区地形地貌发育的重要因素。

首先利用ArcGIS9.2的水文分析模块将研究区划分为31个流域，经统计分析计算获得每个流域研究单元内的多年平均降雨量的平均值Rs，将其作为降雨因素的一种定量指标;然后以DEM为基础，经统计分析计算获取每小流域研究单元的Strahler积分S(表1)。

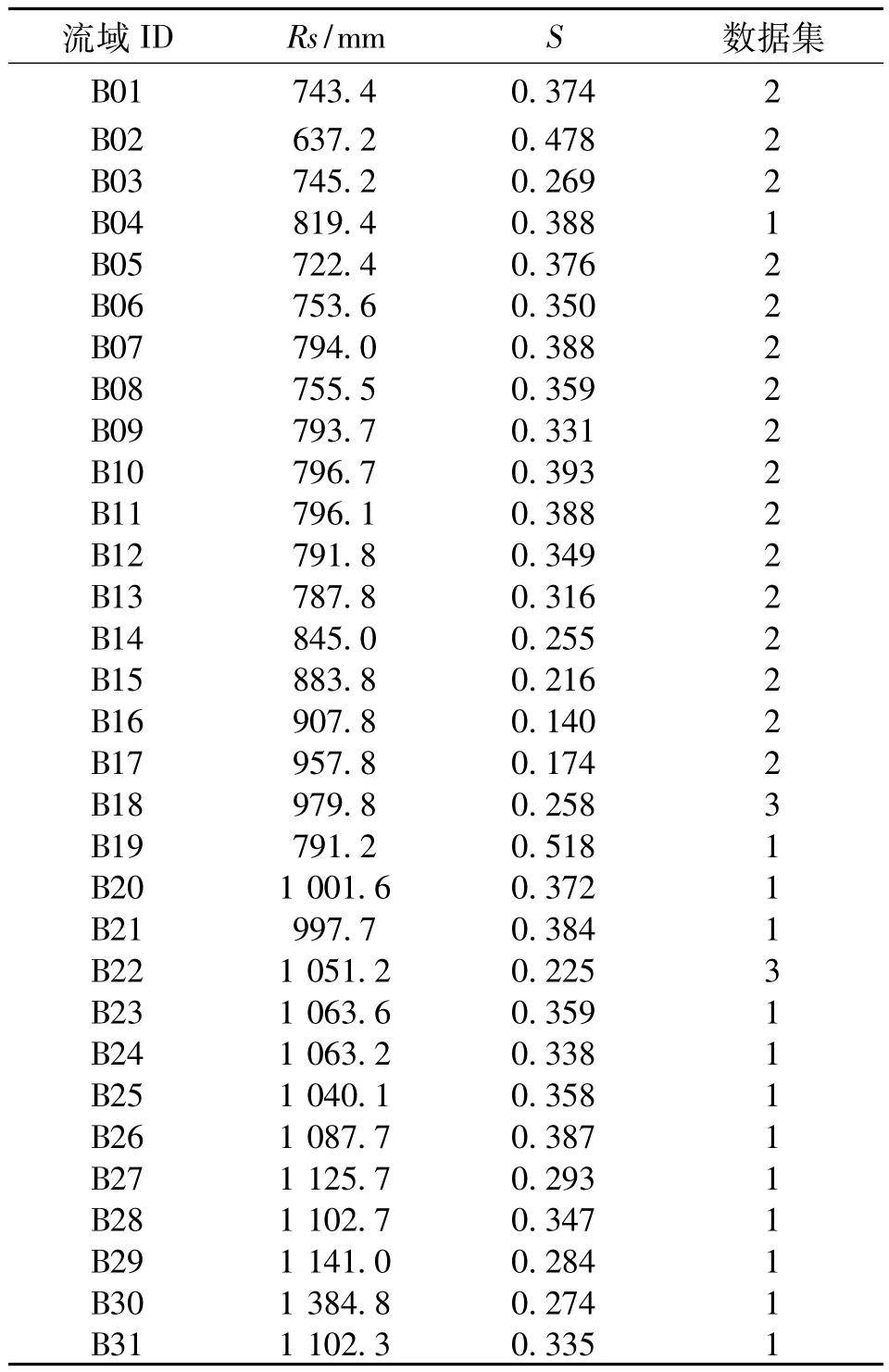
表1 研究区流域研究单元基本数据

对研究区的Rs和S数据进行聚类分析，将研究区数据分为3个数据集(表1)。整体上，研究区小流域的S与Rs存在两种主要关系。数据集1存在函数关系:

数据集2存在的函数关系:

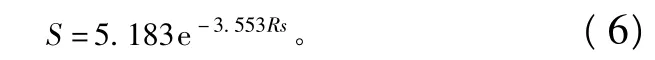
数据3由于数据量有限未做分析。数据1，2和3的整体分布趋势如图4所示。

通过上述分析，地貌指数Strahler积分S与降雨因素存在一定的函数关系。在不同区域受地质条件的影响，不同区域的地貌指数Strahler积分S与不同降雨因素的定量指标存在不同的函数关系。但多年平均降雨量只是降雨因素的一种。

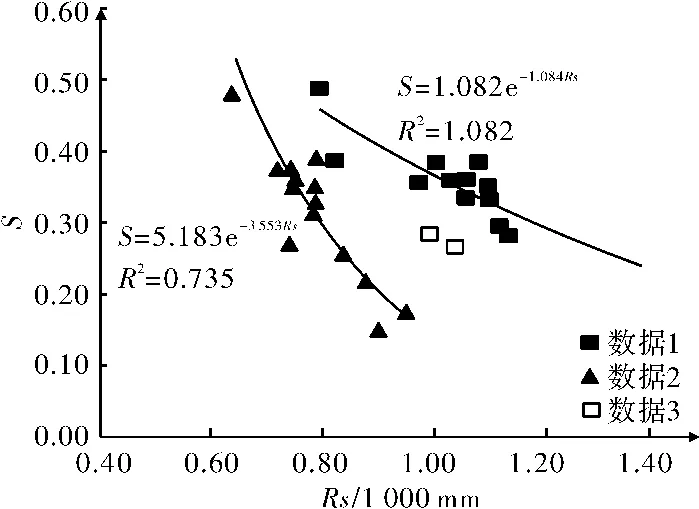
图4 研究区小流域的S与Rs关系图

为进一步研究地貌发育状态与降雨因素之间的影响关系。选择研究区内岷江上游24条小流域(表2);研究分析地貌指数与降雨因素R(年日最大降雨量)之间的关系。研究结果表明，该区域内的小流域地貌指数S与降雨因素R的存在一定的函数关系(图5):

图5 岷江上游小流域的S与R关系图

综上所述，地貌发育状态与降雨因素存在一定关系。在大流域范围内，Strahler积分S与年降雨量Rs存在一定函数关系;在小流域(泥石流单沟)范围内，Strahler积分S与年日最大降雨降雨量R存在一定关系。

2.2 引入地貌指数的泥石流总量计算方法

地貌是内外营力相互作用的结果;地貌状态是对内外营力相互作用的外在体现。地貌指数Strahler积分S是面积与高程的函数积分，是对地表形态的定量化参数;地质条件会影响地貌发育的快慢程度;加上地貌指数S与区域的降雨因素存在关系。因此，地貌指数Strahler积分S包括地形、地质条件和降雨因素三方面的信息。

公式(1)和(2)考虑地形、物源补给及降雨三方面因素，由于地貌指数S包括地形、地质条件和降雨因素方面的信息;因此，引入地貌指数S时公式(2)和(9)中的参数ln A、B0.5的系数都会改变。结合岷江上游24条泥石流沟小流域基本数据，对公式(1)和公式(2)进行改进:

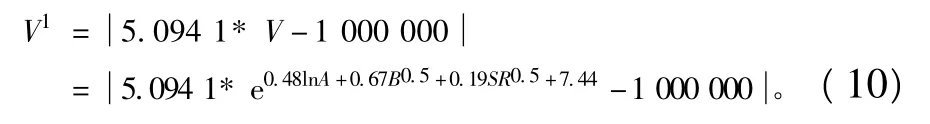
由公式(2)和公式(10)计算出24条泥石流沟的泥石流总量V2、V9(表2):V2、V9两者的相关系数(Person系数)达到0.868，除去离群值后Person系数高达0.932。

表2 岷江上游泥石流沟基本参数及其泥石流总量计算值［4］

综上所述，在缺乏降雨数据的情况下，在一定区域内用地貌指数S计算泥石流总量能够取得较理想的结果，能够解决缺乏降雨数据情况下的泥石流总量计算问题。

3 实例分析研究

清平乡地处四川省绵竹市西北部山区的绵远河上游，属沱江正源。该区域在汶川地震中形成大量的崩塌、滑坡体，导致该区域的泥石流活动频发，灾害更加严重。

2010年08月12 －13日和18－19日在两次区域强暴雨作用下，该区域暴发了大规模、群发性泥石流灾害。由于该区域泥石流物源主要是由地震诱发的崩塌、滑坡体形成的固体松散物质，故适合于公式(9)计算泥石流总量。

根据绵远河上游泥石流沟的基本参数按照公式(9)进行计算，得到泥石流总量的计算结果(表3)。对比“8.13”群发性泥石流事件中各泥石流沟冲出固体松散物质总量M与公式(9)的计算结果;对于本次泥石流事件中冲出固体松散物质总量M小于10×105m3泥石流沟的计算泥石流总量V1明显偏大;但对于规模大于100×105m3的泥石流计算结果偏小。为便于分析分析原因，按照公式(8)计算泥石流总量V(表3)。同样对比V与M;在M小于10×105m3的情况下，V在多数情况下相比V1接近M;但在M大于10×105m3的情况下，V明显偏小。因此，直接以云南蒋家沟数据为基础计算出的适合于受地震影响以崩塌、滑坡体为主要物源的泥石流总量计算公式(2)在研究区域的“8.13”群发性泥石流事件适用性上存在一定局限性。

表3 绵远河上游泥石流沟基本参数及泥石流总量计算值［10］

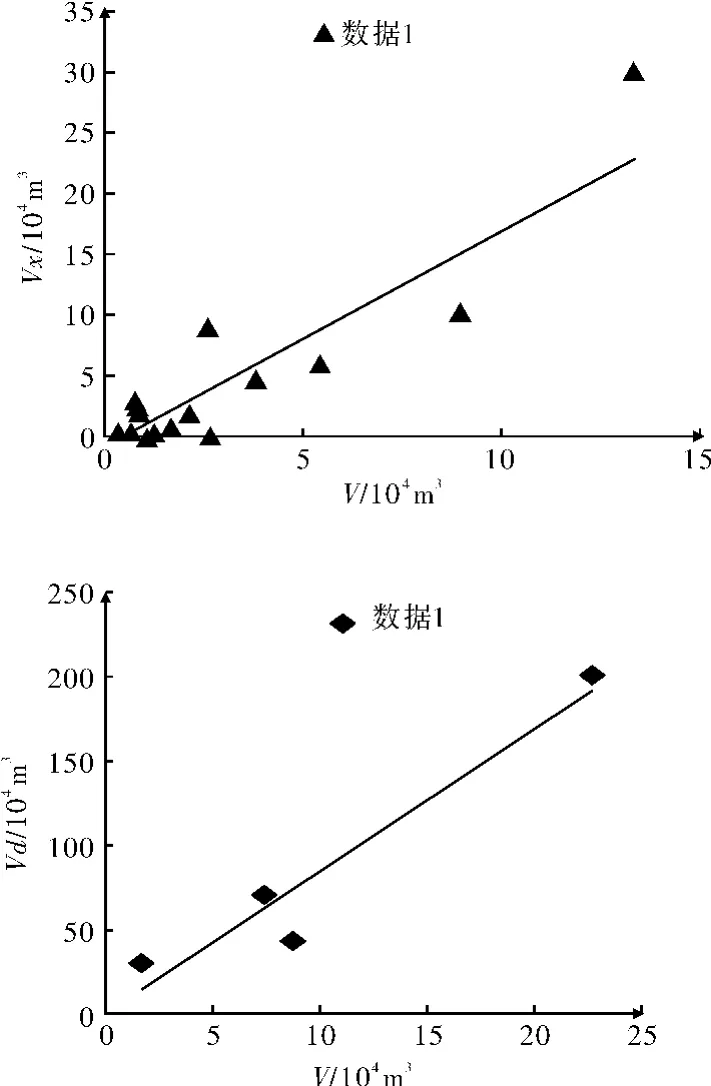
图6 泥石流总量Vx，Vd与V之间的关系

由于公式(2)是以公式(1)为基础，参考云南蒋家沟数据改进获得。但云南蒋家沟的泥石流形成条件与汶川震区存在一定的差异;因此公式(2)计算得到泥石流总量在汶川震区存在差异，即公式(2)在汶川震区存在适用性局限性。为研究适合于汶川震区的泥石流总量计算方法;对“8.13”泥石流事件中泥石流的基本数据进行分类，将研究区数据分为两类(表3)。提出部分离群值后，对于数据1(Vx)和数据2(Vd)与公式(8)计算结果V存在函数关系:

式中:Vx、Vd和 V的单位是104m3。由于公式(11)是根据区域泥石流计算获得，且数据量有限;其在其他区域的适用性有待进一步验证。

通过本实例得到初步结论:适合于受地震影响以崩塌、滑坡体为主要物源的泥石流总量计算公式(2)是区域性经验公式。但公式(2)对受火烧影响区域的泥石流总量计算公式(1)的改进很成功。在不同区域，泥石流总量与公式(1)的计算结果可能存在不同的函数关系;因此在实际运用中应该参考临近区域泥石流数据确定泥石流总量与公式(1)计算结果的函数关系;但对于部分泥石流仍较难计算。

4 结论

地貌发育状态是内外营力相互作用的结果;地貌指数能够体现影响地貌的内外营力的多方面信息，包括地质构造、降雨等方面的信息。本研究将地貌指数Strahler积分S用于泥石流总量的计算;尝试解决缺乏降雨数据情况下泥石流总量计算问题。但由于不同区域形成泥石流的条件存在差异，泥石流总量计算较难形成统一的计算公式。根据“8.13”清平群发性泥石流数据对泥石流总量计算公式进一步改进，初步得到该区域的泥石流总量计算模型。

总体上，适合于受地震影响以崩塌、滑坡体为主要物源的泥石流总量计算公式(2)在汶川地震灾区存在局限性;对于汶川震区泥石流总量的计算方法还需要根据该区域的泥石流实测数据进行改进完善。本研究根据绵远河泥石流实测数据对公式(1)进行了初步改进，并得到该区域泥石流总量初步计算公式;其计算结果具有一定的参考价值;但需要根据更多的数据进行改进和完善。

［1］Rickenmann D．Empirical relationships for debris flows［J］．Natural Hazards，1999，19:47 －77．

［2］Gartner JE，Cannon SH，Santi PM，etal．Empiricalmodels to predict the volumes of debris flows generated by recently burned basins in the western U．S．［J］．Geomorphology，2008，96:339－354．

［3］Cannon S H，Gartner，JE，Rupert M G，et al．Predicting the probability and volume of postwildfire debris flows in the intermountain western United States［J］．Geological Society of America Bulletin，2010，122(1/2):127－144．

［4］庄建奇，崔鹏，葛永刚，等．“5·12”地震后都汶公路沿线泥石流沟危险性评价［J］．四川大学学报:工程科学版，2009，41(3):131－139．

［5］崔鹏，韦方强，陈晓清，等．汶川地震次生山地灾害及其减灾对策［J］．中国科学院院刊，2008，23(4):317－323．

［6］谢洪，钟敦伦，矫震，等．2008年汶川地震灾区的泥石流［J］．山地学报，2009，27(4):501－509．

［7］崔鹏，韦方强，何思明，等．“5·12”汶川地震诱发的山地灾害及其减灾措施［J］．山地学报，208，26(3):280－282．

［8］艾南山．侵蚀流域系统的信息熵［J］．水土保持学报，1987，1(2):1－8．

［9］艾南山，岳天祥．再论侵蚀流域系统的信息熵［J］．水土保持学报，1988，2(4):1－9．

［10］苏鹏程，韦方强，冯汉中，等．“8·13”四川清平群发性泥石流灾害成因及其影响［J］．山地学报，2011，29(3):337－347．

Method of Calculating Single Gully Debris-flow Volume in W enchuan Earthquake Area Based on M orphometric Index

Zhang Huaizhen1，2，3and Fan Jianrong1
(1．Key Laboratory of Mountain Hazards and Surface Process，Chengdu Institute of Mountain Hazards and Environment，CAS Sciences，Chengdu 610041，China;2．Institute of Mountain Hazards and Environment，CAS＆ Water Resources，Chengdu 610041，China;3．Graduate University of the Chinese Academy of Sciences，Beijing 100049，China)

Most available equations for estimating amaximum debris-flow volume have the limitation in requiring uncertain input parameters．In addition，landslips and landslides that occurred in the debris-flow source area of the Wenchuan earthquake zone contributed extensively to the debris-flow volume．Most equations have the limitation in this area．This study is based on an equation that is fit for debris-flow in earthquake zone．The relationships among morphometric condition，rain and other geological conditions are analyzed．The morphometric index(Strahler Integration)is tentatively used to calculate debris-flow volume when rain condition data are unavailable．A model suitable for calculation of debris-flow volume ofWenchuan earthquake zone isworked out based on regression analysis of the data of group debris-flows in Qingping Town，Mianyuan River Upstream，Sichuan．

single debris-flow volume;Wenchuan earthquake zone;Morphometric Index;rain

P642.23

A

1000－811X(2012)03－0086－06

2011－11－22

2012－02－06

国家科技支撑计划课题(2011BAK12B03)

张怀珍(1985－)，男，山东东昌府区人，硕士研究生，主要研究方向为环境遥感与GIS应用．E-mail:zhz198508@163.com

范建容(1969－)，女，四川井研县人，博士，研究员，主要研究方向为环境遥感与水土保持．E-mail:fjrong@imde.ac.cn