基于灰关联分析的时间序列改变点搜索研究*——以华东地区农业受灾面积序列为例

张 云，巩在武

(南京信息工程大学经济管理学院，江苏南京210044)

基于灰关联分析的时间序列改变点搜索研究*
——以华东地区农业受灾面积序列为例

张 云，巩在武

(南京信息工程大学经济管理学院，江苏南京210044)

采用灰关联分析方法，构建了短时间序列中的改变点搜索算法，有效地解决了短时间序列改变点寻找的缺陷。首次将灰关联度算法应用到气象灾害时间序列改变点的搜索中，利用华东地区农业受灾面积时间序列实例来验证灰关联度算法的实用性和有效性。结果表明，用灰关联方法可以有效地获得改变点，并以此对时间序列的发展规律进行趋势与规律分析。

改变点;时间序列;灰关联分析;农业受灾面积

0 引言

在一组随机时间序列中，受某种因素的影响，从某一点开始出现一个明显的改变趋势或表现为跳跃趋势，这个点就是改变点。改变点的分析有助于从随机独立序列中发现规律并应用到生活生产中，以便提前采取相关应对措施，迄今为止，许多学者在改变点的寻找和测验方面取得了显著成果。Hurst于1951年提出了对改变点的研究［1］，其后 Hinkley［2］，Brown 等［3］学者在此基础上做出了更深一步的探索。

Smith［4］在1975年较早提出用贝叶斯法去分析随机变量序列的改变点问题，Carlin等［5］在此方面又做出了进一步研究。Lee和 Heghinian［6］在1977年提出的新贝叶斯方法被Bernier［7］等人用到水文气象、气候变异等研究中;Rao和Tirtotjondro［8］在1996年用贝叶斯方法描述一个变量发生在水文随机序列中的时间及其变化多少;Perreault［9－10］等人在2000年首次从贝叶斯角度来寻找水文序列中的改变点，建立了简单的改变点模型并进行对比及检测。在改变点寻找方面，上述学者基本上采用了统计学的方法。然而，数理统计方法对大样本数据量要求较高，无法解决小数据量时间序列改变点的搜寻问题。此外用数理统计方法处理数据的过程复杂繁琐，很难有效地获得改变点。

灰色系统强调用少量的数据分析发现问题的实质，解决了统计学方法寻找改变点带来的一些缺陷［11］。灰色关联分析是通过灰色关联度来分析和确定系统诸因素间的影响程度或因素对系统主行为的贡献程度的一种方法，已经被广泛地应用到预测、决策、评估、经济计量、模式识别、聚类分析、系统指标权重确定等领域［12］。气象灾害改变点的研究对了解气象灾害的发生、发展以及应对措施的选取具有重大意义。迄今为止，灰关联方法尚未被用到灾害时间序列改变点的选择中。由于灰关联分析方法对数据样本容量大小无特殊要求，本文拟采用灰关联分析方法研究灾变时间序列的改变点的搜索问题，并以华东地区农业受灾面积为案例，采用灰关联算法确定农业受灾面积时间序列的改变点。

1 主要研究内容

1.1 基础理论与算法

1.1.1 灰关联理论介绍

灰色关联分析的基本思想是根据序列曲线几何形状的相似程度来判断其联系的紧密程度。曲线之间的相似性程度越大，则相应数据列之间的关联度也就越大，反之就越小。灰色关联分析方法弥补了常规多元统计分析方法的上述缺陷，即它对样本量的多少和样本有无规律都同样适用，而且计算量小，十分方便，更不会出现量化结果与定性分析结果不符的情况［12］。灰关联度已经在经济、管理、模式识别、聚类分析及控制理论中得到广泛应用。根据文献［11］的研究结果，有:

定义1 设X0=(x0(1)，x0(2)，…，x0(n))为系统特征序列，Xi=(xi(1)，xi(2)，…，xi(n))，i=1…m为相关因素序列。给定实数γ(x0(k)，xi(k))，若实数 γ(X0，Xi)=(k)，xi(k))满足规范性、整体性、偶对称性和接近性，则称γ(x0(k)，xi(k))为Xi与X0的灰色关联度，γ(x0(k)，xi(k))为Xi与X0在k点的关联系数。

定理1 设系统行为序列Xi={xi(1)，xi(2)，…，xi(n)}，i=1，2，…，m为相应固定序列。对于ξ∈(0，1)，令

ξ∈(0，1)称为分辨系数，γ(X0，Xi)称为 X0与Xi，i=1，2，…，m的灰色关联度。灰色关联度γ(X0，Xi)常简记为 γ0i，k点关联系数 γ(x0(k)，xi(k))简记为 γ0i(k)。γ0i，i=1，2，…，m 也称为邓氏关联度，邓氏关联度满足规范性、整体性、偶对称性、接近性。

下面，我们将灰关联度用在时间序列改变点的确定中。

1.1.2 改变点的灰关联度搜索算法

用灰关联来寻找改变点的算法总结如下。

步骤1:构建参考序列 从时间序列X=(x(1)，x(2)，…，x(n))，x≥10的前半列(或者后半列)中选取X0=(x(1)，x(2)，…，x(T))，5≤Ts≤T≤Te≤［n/2］作为参考序列，其中Ts≤Te并且Ts，T和Te都为整数。

步骤2:构建比较序列 在参考序列X0=(x(1)，x(2)，…，x(T))，5≤Ts≤T≤Te≤［n/2］的基础上，比较序列如下:

将式(3)定义为阶数为n－2T+1的比较序列集。

步骤3:计算整体关联程度 分别计算X0和X1，X2，…，Xn－2T+1的关联度 r1(T)，r2(T)，…，rn－2T+1(T)。然后求这些关联度的算术平均值:

我们不妨称r(T)，5≤Ts≤T≤Te≤［n/2］为 T－整体关联度。

步骤4:确定改变点

需要注意的有以下几点。

(1)如果改变点出现在时间序列S=(s(1)，s(2)，…，s(n))的后半部分，则做如下变化:

x(k)=s(n－k+1)，k=1，2，…，n。

(2)如果关联度r(T)=0，式(5)可改写为:

(3)从理论上考虑，Ts可以取1，但是当Ts取非常小的值时，本文的方法将失去意义。所以，在数值应用中，我们应该合理地选择Ts，例如Ts应大于等于5。

1.1.3 特殊序列(非规则的单增和单减数列)改变点的确定

下面我们将研究不规则的单增和单减序列中改变点的确定问题。

设单调序列为X=(x(1)，x(2)，…，x(n))，n≥10。通过大量的数据实验仿真，我们发现在运用灰关联算法求改变点的过程中，无论序列X是一个单调递增数列还是一个单调递减序列(即使序列中存在极度异常点，比如某些急速上升或者下降)，改变点始终是序列中第［n/2］－1个数。

灰关联算法为寻找改变点提供了一种新的方法，但是必须指出的是，这种算法也存在一些缺陷。例如序列 S1(2，4，8，16，32)和 S2(64，128，256，512，1024)，这两组数列用 COS余弦函数求出的关联度是1，但是用灰关联算法得出的两组数列的关联度则是0.637 8。从多维空间角度分析，这两组数列在空间里是平行的，所以它们的关联度是1是合理的。从这个意义上讲，灰关联算法实质上是基于二维平面时间序列算法，其在求空间时间序列时存在一定的缺陷。

1.2 灰关联理论在农业灾害时间序列改变点选择中的应用

虽然灰关联算法在多维空间时间序列的寻找上存在缺陷，但并不影响我们在平面时间序列上寻找改变点。下面我们将用灰关联的算法，寻找华东地区(山东省、江苏省、江西省、浙江省、安徽省、福建省和上海市)1970－2009年农业受灾面积时间序列的改变点，也以此验证本文的灰关联算法的有效性。这里我们分别选取文献［13］中1970－2009年华东地区农业雨涝灾害面积、干旱灾害面积和农业受灾总面积三个时间序列来进行分析。

1.2.1 华东地区农业雨涝灾害改变点的选择

1970－2009年华东地区农业遭受雨涝灾害的面积如图1所示。表1中给出了基于灰关联算法的华东地区农业雨涝灾害面积的相对T－整体关联度的数值结果。

图1 华东地区1970－2009年遭受雨涝的农业受灾面积

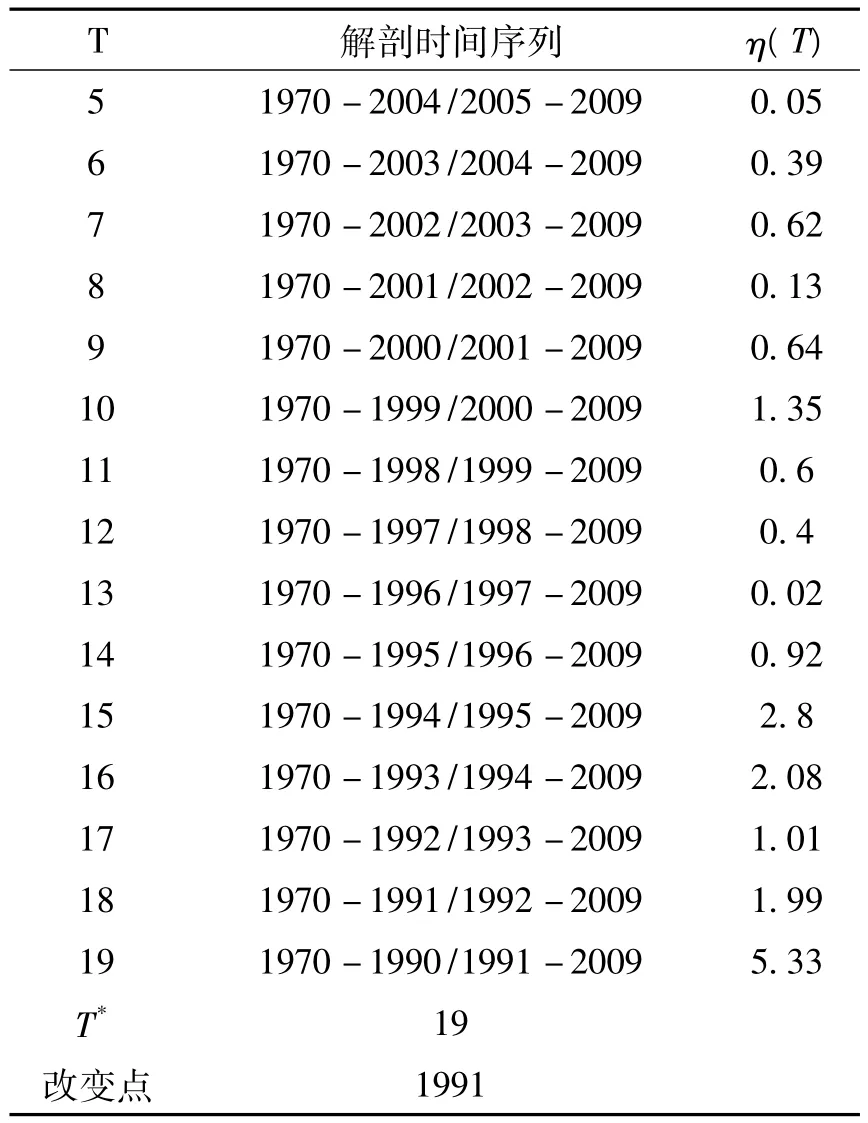
表1 华东地区雨涝受灾面积序列相对各种比例的关联度和各种程度的的数值结果

从表1中我们可以发现T*=19，即相对T-整体关联度中的最大值是η(19)，因为该改变点位于数列的后半部分，我们是从后半列选取参考序列，所以改变点位于该时间序列的22个，也就是1991年。从图1中我们可以明显地看出1991年的数据峰值最大，这一年遭受雨涝灾害的农业面积远大于其它年份，而这正和我们用灰关联算法得出的结果一致。

1.2.2 华东地区农业干旱灾害改变点的选择

图2是1970－2009年华东地区农业干旱灾害面积示意图。

经过计算我们发现T*=9，即相对T-整体关联度中的最大值是η(9)，因为改变点位于数列的后半段，我们是从后半列选取参考序列，所以可知改变点位于该时间序列的第32个，也就是2001年。从图2我们可以明显的看出从1970年到2000年华东地区农业遭受干旱灾害一直很频繁，并且农业受灾面积的峰值很高，而从2001年开始农业受灾面积呈递减趋势，递减幅度很大，遭受旱灾的农业面积呈现低幅度发生的趋势。而前面我们用灰关联算法找到的改变点正是2001年，与分析所得的实际情况相符合。

图2 华东地区1970－2009年遭受干旱灾害的农业受灾面积

1.2.3 华东地区农业灾害总面积改变点的选择

图3是1970－2009年华东地区农业灾害总面积示意图。表2表3给出了基于灰关联算法的华东地区农业灾害总面积的相对T-整体关联度的数值结果。

图3 华东地区1970－2009年遭受的农业受灾总面积

表2 相对各种比例的关联度和各种程度的农业受灾总面积序列的数值结果

表3 相对各种比例的关联度和农业受灾的总面积的各种程度的数值结果

从表2我们可以发现T*=17，即相对T-整体关联度中的最大值是η(17)，因为该改变点位于数列的前半段，我们是从前半列选取参考序列，所以此改变点位于该时间序列第17个，也就是1986年;从表3中我们得出T*=11，即相对T-整体关联度中的最大值是η(11)，因为该改变点位于数列的后半部分，我们是从后半列选取参考序列，所以改变点位于该时间序列第30个，也就是1999年。首先我们将图3的时间序列分成两部分，即从1970－1998年和从1999－2009年，通过分别对这两部分添加趋势线(图4)。我们发现:从1970－1998年华东地区农业受灾总面积呈递增趋势;而从1999－2009年该地区的农业受灾总面积则呈现递减趋势。从分析可知1999年是这个时间序列的改变点，这和我们用灰关联算法得出的结果相同。

图4 华东地区1970－2009年农业受灾总面积趋势

如果将图3的时间序列分成三部分，即分为1970－1986年，1987－1999年，2000－2009年三个时间段。通过对这三部分的图分别添加趋势线(图5)，我们发现:从1970年到1986年，时间序列呈低增长趋势，华东地区农业受灾总面积每年缓慢增长;从1987年到1999年，时间序列虽然有缓慢递增趋势，但递增趋势很小，而且从图5中我们可以看出这一时间段的数值明显高于其它两个时间段的数值，近乎呈现高位、平稳状，即该地区在这些年里频繁遭受灾害，并且农业受灾总面积峰值在这一段时间里一直很高;2000－2009年，时间序列呈递减趋势，华东地区的农业受灾面积逐渐减少。通过分析我们得到的两个分界点1986年和1999年正好是表2和表3中我们用灰关联算法得出的改变点。

图5 华东地区1970～2009年农业受灾总面积趋势

此外，通过查阅我国GDP的发展情况［13］，我们发现在1987－1999年华东地区受灾面积一直处于高位。这段时间正是我国改革开放后经济迅猛发展的时期，很多地区都以破坏自然环境为代价来获取GDP的高速发展。从2000年以后，随着我国GDP增长的减缓，国家对自然环境大力治理，加强了对自然灾害的防御措施，华东地区的农业受灾面积开始逐渐减少。这一历史情况恰好和我们用灰关联算出的改变点相符合。

2 结论与展望

本文利用灰色关联分析，研究了改变点搜索的灰关联算法问题。针对短时间序列中的改变点搜索问题，统计学方法要求大数据量，无法解决小数据量时间序列改变点的搜寻问题，此外用数理统计的方法处理数据的过程复杂繁琐，很难有效地获得改变点。本文采用灰关联分析方法，构建了短时间序列中的改变点搜索算法，该算法的优点是计算速度快且改变点寻找方便，有效地解决了统计学方法在短时间序列改变点寻找中的缺陷。本文首次将灰关联度算法应用到气象灾害时间序列改变点的搜索中:利用华东地区农业受灾面积序列为实例，验证了灰关联度算法的实用性和有效性，实际分析表明，用灰关联方法可以有效地获得改变点，并在此基础上对时间序列的发展规律进行趋势与规律分析。

本文还初步研究了特殊时间序列中的改变点确定问题，在未来研究中，我们将从理论层面探讨基于灰关联的特殊序列改变点选择问题;同时探索基于灰关联的改变点搜索算法在时间序列周期划分及在社会经济领域的应用问题。

［1］HE Hurst．Long-term storage capacity of reservoirs［J］．Trans．Am．Soc．Eng，1951，116:770－808．

［2］DV Hinkley．Inference about the change-point in a sequence of random variables［J］．Biometrika，1970，57(1):1 －17．

［3］RL Brown，JDurbin，JM Evans．Techniques for testing the constancy of regression relationshipsover time(with discussion) ［J］．Journal of the Royal Statistical Society，1975，B37(2):149－192．

［4］AFM Smith．Bayesian approach to inference about change-point in sequence of random variables［J］．Biometrika，1975，62(2):407－416．

［5］BPCarlin，AE Gelfand，AFM Smith．Hierarchical Bayesian analysis of change-point problems［J］．The Applied Statistics，1992，41(2):389－405．

［6］Lee ASF，Heghinian SM．A shift of themean level in a sequence of independent normal random variables-a Bayesian approach［J］．Technometrics，1977，19(4):503－506．

［7］Bernier J．Statistics detection of changes in geophysical series［C］//Duckstein L，Parent E．Engineering risk in Natural Resources Management．NATO Advanced Studies Institute Series Kluwer，Dordrecht，1994:159 －176．

［8］AR Rao，Tirtotjondro W．Investigation of changes in characteristics of hydrological time series by Bayesianmethod［J］．Stochastic Hydrology and Hydraulics，1996，10(4):295－317．

［9］Perreault L，Bernier J，Bobee B，et al．Bayesian change-point analysis in hydrometeorological time series．Part 1，The normal model revisited［J］．Journal of Hydrology，2000，235(3/4):221－241．

［10］L Perreault，JBernier，B Bobee，et al．Bayesian change-point analysis in hydrometerorological time series．Part 2，Comparison of change-pointmodes and forecasting［J］．Journal of Hydrology，2000，235(3－4):242－263．

［11］刘思峰，党耀国，方志耕．灰色系统理论及其应用［M］．北京:科学出版社，2004．

［12］孙玉刚．灰色关联分析及其应用的研究［D］．南京:南京航空航天大学，2009．

［13］中国统计局．中国统计年鉴［M］．北京:中国统计出版社，1970－2009．

Change-point Searching of Time Series based on Grey Relational Analysis——Taking Sequences of Agricultural Disaster Area in East China as an Example

Zhang Yun and Gong Zaiwu
(College of Economics and Management，Nanjing University of Information Science and Technology，Nanjing 210044，China)

An algorithm is constructed with grey relational analysis to detect change-points in short time series，which effectively overcomes shortages of the existing statisticalmethods．The grey relational algorithm is firstly applied to the change-point searching of time series in meteorological disasters．Sequences of agricultural disaster area in East China are used to show validity and practicability of the algorithm of new grey relational method．The results indicate that the grey relational algorithm can effectively get the change-point．And in this case，the trends and laws of time series characters can be developed．

change point;time series;grey relational analysis;agricultural disaster-stricken area

S42

A

1000－811X(2012)03－0064－05

2011－12－22

2012－02－27

国家自然科学基金资助项目(70901043，71171115);教育部人文社科基金(09YJC630130)

张云(1991－)，女，江苏宿迁人，大学本科，主要从事气象风险评价研究．E-mail:821965313@qq.com

巩在武(1975－)，男，山东临沂人，副教授，硕士生导师，主要从事气象风险评价、灰色系统理论．E-mail:zwgong26@163.com