具有自由液面效应的圆柱绕流三维数值模拟

岳永威 李梦阳 孙龙泉 王 领

（哈尔滨工程大学 船舶工程学院 哈尔滨 150001）

0 引 言

随着海洋工程的飞速发展，越来越多的圆柱结构物出现在实际工程中，如海洋工程中的立管、平台、水下输油管道等，与之紧密相关的圆柱绕流问题也日益成为科研领域关注的热点［1］。目前，国内学者关于圆柱绕流的研究成果大多是基于深海、二维条件下得出的，计及自由液面效应的三维圆柱绕流问题的文献并不多见，许多自由液面作用下海洋结构物绕流特性的现象和本质还没有被揭示。事实上，当结构穿透自由液面时，物体表面的粘性效应将会被激发，因自由液面而产生的这种效应会对结构物周围的流场特性产生影响［2-4］。因此，有必要对圆柱绕流在自由液面影响下的水动力特性进行分析，进而为相关的理论研究和工程设计提供依据。

随着数值方法和计算机模拟技术的发展，数值模拟由于建模简便、计算成本低、流场可视化等优点，逐渐成为研究圆柱绕流问题的一种重要手段［3-4］。本文基于计算流体力学软件CFX，应用RNG k-ε湍流模型，结合VOF方法，在雷诺数为104～105、傅汝德数为0.15～0.88范围内，研究均匀流场中半沉浸三维圆柱穿透自由液面的绕流问题，分析自由液面对圆柱尾迹的影响以及不同雷诺数和傅汝德数情况下的流场特性，通过总结圆柱水动力特征系数随流场傅汝德数和雷诺数的变化规律，得出具有自由液面时圆柱绕流的水动力特性。

1 自由面圆柱绕流的数值模拟

本文利用计算流体力学软件CFX建立自由面圆柱绕流的数值模型，设定圆柱的直径为D，综合考虑三维圆柱在流场中大涡模拟方法、涡激振动、展向长度效应等［3-5］，最终确定流场的尺度，如图1所示。

图1 数值实验模型结构图

入口设置为均匀流入口，流速为u。假设出口为无穷远，设置其为静压出口，即x→∞时，压强为:

其中，P0为流场的参考压强，ρ为流场的密度997 kg/m3，g为重力加速度，h为水深。流场底部、前后壁面均为壁面边界条件，在流体与固体的交界面处，流体与固体无相对滑移。三维刚性圆柱边界条件为:三维圆柱为刚性无滑移，即un=0。

对于非定常的粘性流动，需给出初始时刻（t=t0）时流场中各有关物理量的分布，即流动的初始条件。本文基于CFX-5系列软件通过VOF法［6］求解得到整个流场的初始水深为4D。

在得到流场的边界条件和初始条件后，应用RNG k-ε湍流模型，结合VOF方法模拟自由液面，便可对半沉浸圆柱的流动进行数值模拟。数值计算选取雷诺数在104～105，傅汝德数在0.15～0.88范围内进行，数值计算工况见表1。

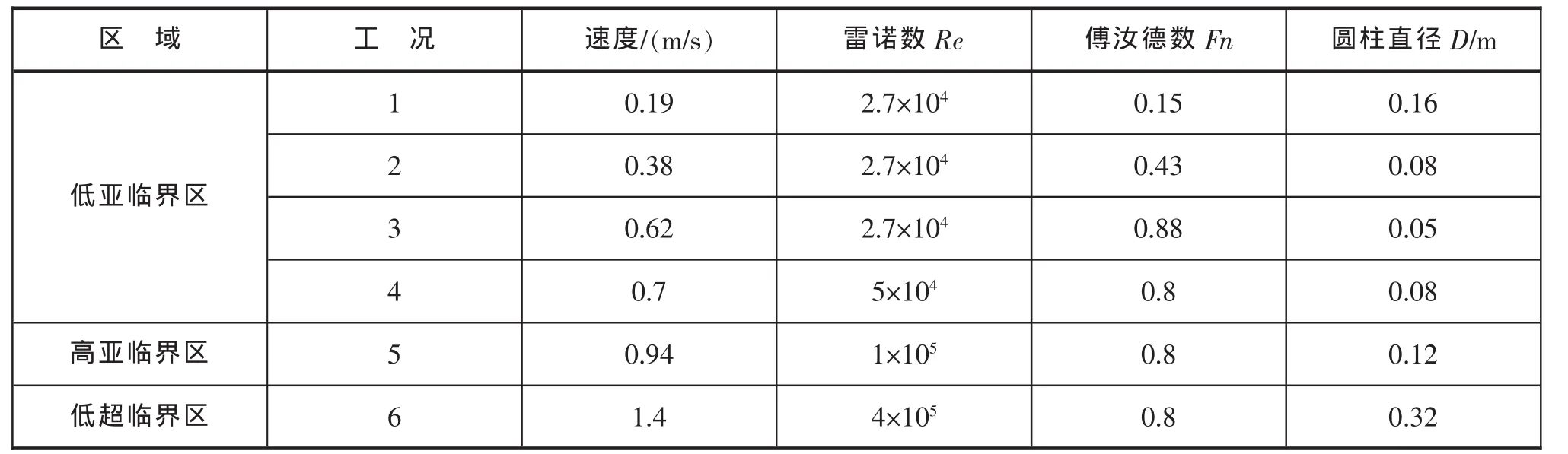
表1 数值计算工况

2 自由面对圆柱绕流流场尾迹的影响

圆柱绕流的三维数值模拟在不同的展向范围内可以描述不同的漩涡泄出形式［7］，其数值模拟的结果因不同吃水圆柱截面的漩涡泄出的形式而不同。为了较全面研究自由面对圆柱绕流流场尾迹的影响，本文分别取吃水深度为0D、1D、2D、4D的圆柱截面，进行卡门涡街比较。图2和图3分别为不同傅汝德数、不同雷诺数时，各圆柱截面瞬时涡量云图。

图2为Re=2.7×104的瞬时涡量分布。可以看出当傅汝德数较小时，在自由液面处圆柱表面的边界层向下游泄出，圆柱背部形成一个涡对后，漩涡的能量减小。在自由液面作用下，流场绕流圆柱后形成周期性的漩涡脱落，随着吃水的增加，自由液面的影响效应很快减弱。傅汝德数较大时，在自由液面附近，自由液面波动干扰把大尺度漩涡转化成大量随机的小尺度漩涡；Z=-1D时，圆柱表面的边界层在圆柱背部由于受到自由液面的影响，泄出较短即产生漩涡脱落，没有形成明显的卡门涡街现象；Z=-2D和Z=-4D时，边界层向下游泄出，周期性的漩涡脱落现象很明显，与无限长圆柱的流动相似，自由液面对Z=-2D吃水处的圆柱绕流影响很小。

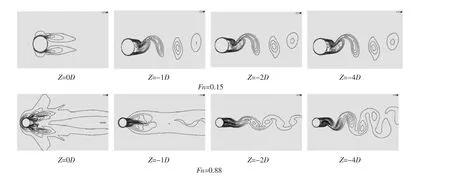
图2 Re一定、Fn不同时，各截面瞬时涡量云图

图3为当Fn=0.8、雷诺数变化时，各展向截面瞬时涡量云图。比较不同雷诺数相同吃水处的瞬时涡量云图发现，雷诺数的变化对圆柱绕流尾涡的影响不大。在自由液面附近，自由液面的波动、变形，使自由液面处的边界层向外泄出，限制大尺度漩涡在自由液面的发展，形成大量随机的小尺度漩涡；Z=-1D时，圆柱表面的边界层在圆柱背部因受自由液面的影响，泄出较短，即生成漩涡脱落；Z=-2D和Z=-4D时，边界层向下游泄出，周期性的漩涡脱落现象很明显，与无限长圆柱的流动相似。由上述分析可知，在Z=-4D时，流场不再受自由液面的影响。

图3 Fn一定、Re不同时，各截面瞬时涡量云图

由于自由液面的影响，不同的雷诺数将对应圆柱绕流展向的不同漩涡泄出形式，用涡量描述展向上不同截面漩涡泄出的涡街形式。涡量是速度的旋度，用符号Ω表示。

以涡量为变量绘制圆柱绕流的三维漩涡泄出等值面图，就可以得到描述圆柱体漩涡三维泄出的涡管［8］。图4～图5为圆柱绕流后不同雷诺数时的涡管图。

图4 Re=2.7×104时不同Fn瞬时涡量管图

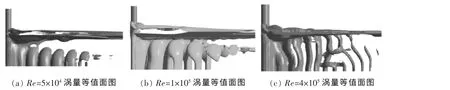
图5 Fn=0.8时不同Re瞬时涡量管图

由图4（a）可以看出，傅汝德数较小时，涡管结构受自由液面的影响很小，与相关文献［9］中的三维无自由液面的圆柱绕流后的涡管结构相似；当傅汝德数增大时，图 4（b）、（c）表明，自由液面对流场尾迹的涡结构作用增大。

由图5（a）、（b）可以看出，在雷诺数Re=5×104和Re=1×105时，自由液面的对流场尾迹的涡结构作用很大。由于自由液面的影响，在卡门涡街的发展过程中，漩涡自柱体脱落后形成的涡管与自由液面分离，表明在雷诺数较小时，自由液面对流场尾迹的涡结构影响较大；当Re=4×105时，自由液面的影响减弱，涡管与自由液面相连接，随着卡门涡街的运动，涡管有些倾斜，自由液面对涡管虽有影响，但作用变小。

综上所述，对于相同傅汝德数的具有自由液面的三维圆柱绕流，当雷诺数较小时，自由液面对流场的作用明显；随着雷诺数增大，自由液面对流场的影响变小。

3 自由面对圆柱绕流水动力特性的影响

与无自由液面的圆柱绕流相比，自由液面作用下的三维圆柱绕流流动特性所表现出的较强三维效应，除了上述尾迹的涡结构，还体现在三维圆柱表面的压力系数、阻力系数等水动力特征参数。自由液面的影响会使三维圆柱的各水动力特性系数沿圆柱展向发生变化，因此本文沿着圆柱展向选取9个截面对这些系数进行分析。三维圆柱展向各个截面如图6所示，计算工况见下页表2。

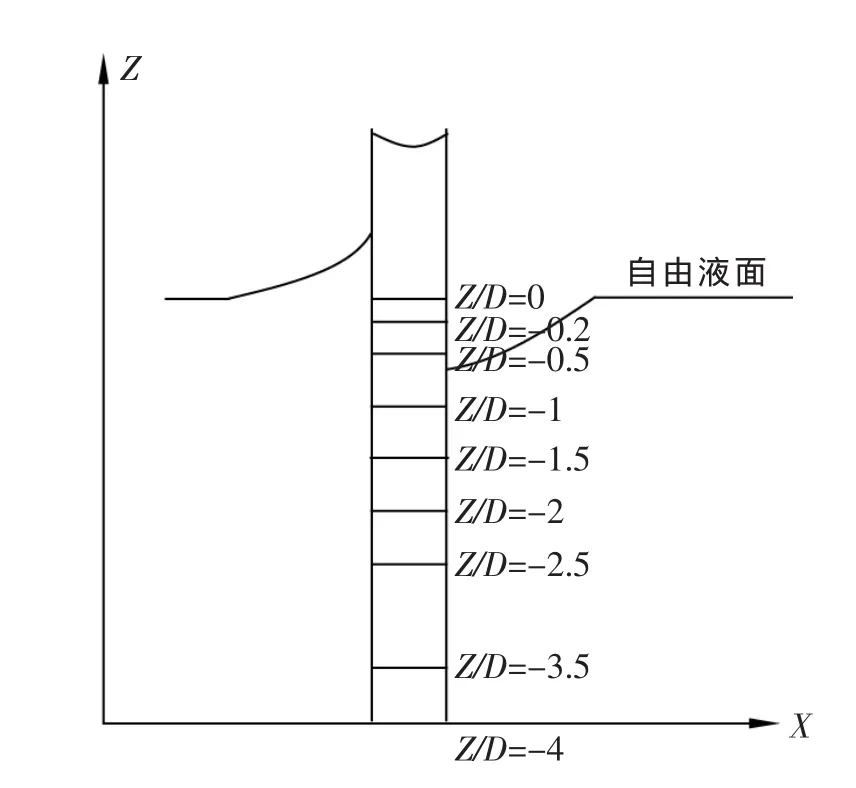
图6 三维圆柱体展向各个截面

表2 三维圆柱体各截面水动力特征参数计算工况

图 7 Re=2.7×104、Fn 不同时，不同截面时均压力系数沿周向分布图

3.1 自由面作用下时均压力系数沿周向分布

圆柱表面所受的时均压力系数Cp，其定义如下:

式中:P为圆柱表面各点的实际压力值，Pa；

P0为无穷远处来流压力，Pa；

V为来流速度，m/s；

ρ为15℃时水的密度，997 kg/m3。

三维圆柱体展向各个截面时均压力系数Cp周向的分布计算结果如图7、图8。

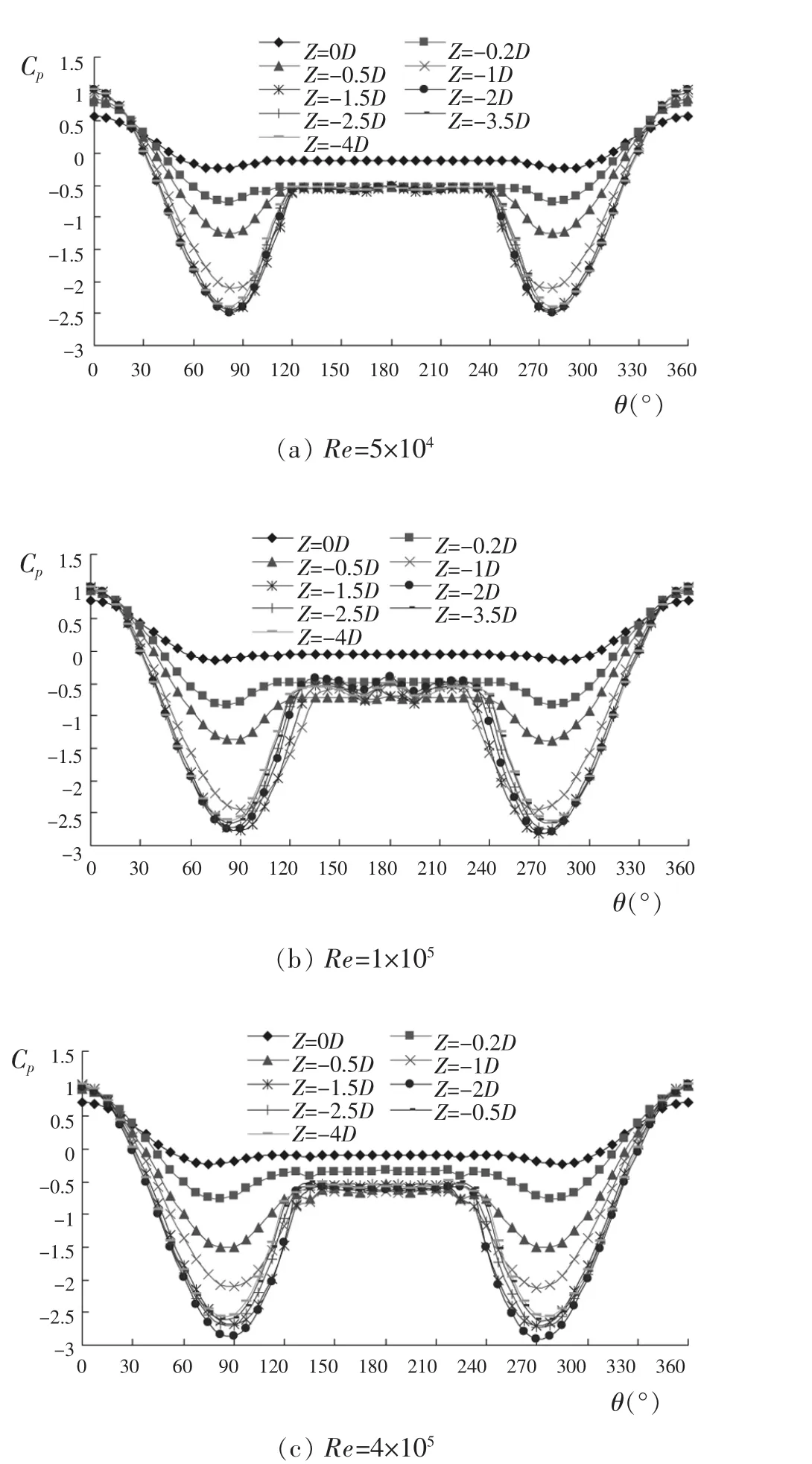
图8 Fn=0.8、Re不同时，不同截面时均压力系数沿周向分布图

图7为雷诺数一定、傅汝德数变化时的时均压力系数沿周向分布图。从图中可以明显看出，不同水深处圆柱截面上的时均压力系数Cp变化趋势基本一致，关于180°周向角对称、在圆柱前驻点最大、随着向圆柱两侧的扩展，Cp迅速减小到最小值；傅汝德数不同时，周向角相同时的时均压力系数Cp的绝对值随着吃水的增加而增加，自由液面对不同水深处圆柱截面的影响也不同。

从图7（a）中看出，傅汝德数为0.15时，在自由液面下，不同截面的周向时均压力系数曲线变化一致，正对来流处驻点（即 θ=0°和 θ=360°时）的时均压力系数Cp最大（约1.0）；周向角θ≈82.5°和θ≈277.5°时，达到极小值（约为-2.38）；背压区的时均压力系数在-0.56附近。7（b）中Z/D=-1之下不同截面的周向时均压力系数曲线变化一致。正对来流处驻点的时均压力系数Cp最大（约1.0）；随着来流向柱体两侧的扩展， 在 θ≈82.5°和 θ≈277.5°时，Cp迅速减小到极小值（约-2.31）；背压区的时均压力系数在-0.6附近。图7（c）中不同截面的周向时均压力系数曲线变化与 7（b）一致。

比较图 7 中（a）、（b）、（c），发现当雷诺数不变、傅汝德数增加时，时均压力系数极小值变化不大，背压区的时均压力系数也没有变化，但自由液面对不同水深处流场的影响随着傅汝德数的增加而增加。

图8为傅汝德数一定、雷诺数变化时的时均压力系数沿周向分布图。从图中可以看出，雷诺数不同时，不同水深处的时均压力系数Cp变化趋势一致；相同周向角的时均压力系数Cp的绝对值随着水深的增加而增加；水深在1.5D下，时均压力系数是一致的，表明没有受到自由液面的影响。

均匀来流的情况下，正对来流处驻点（即θ=0°和θ=360°时）的时均压力系数Cp极大值在1.0附近；随着来流向柱体两侧扩展，在θ≈90°和θ≈270°时，Cp迅速减小到极小值，且此极小值随着雷诺数的增加而减小；在同一雷诺数下，由于自由液面的作用，Cp沿展向分布也是变化的，随着水深的增加而减小。比较图8中（a）、（b）、（c），发现相同傅汝德数时，时均压力系数最低点随着雷诺数的增加而减小；雷诺数的变化对时均压力系数沿展向分布的影响不大。

3.2 自由面对圆柱表面阻力系数的影响

流体的雷诺数和紊流强度对发生涡街时圆柱体上的作用力有一定的影响［10］，在圆柱体绕流的亚临界区，时均阻力系数、脉动阻力系数均随来流紊流强度的增大而减小。在超临界区，这些阻力系数均随来流紊流强度的增大而增大。在具有自由液面的圆柱绕流流场中，傅汝德数也必将对时均阻力系数产生影响。因此本文将分析在自由液面流场中傅汝德数、雷诺数对圆柱表面阻力系数的影响及其沿周向的分布规律。

柱体受到的时均阻力包括由切应力引起的摩擦阻力和由于压力而引起的压差阻力。本文的圆柱假设为光滑的，因此只考虑由压力引起的压差阻力。可利用式（3）将圆柱绕流时各个工况的压差阻力无量纲化，得到时均阻力系数C¯D，计算结果见表3。

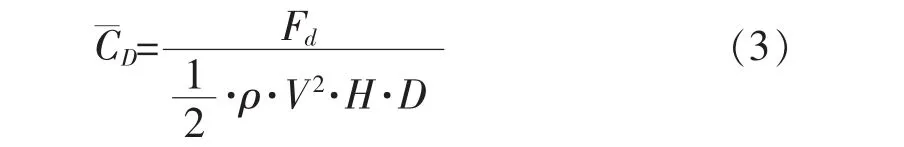
式中:Fd为作用在整个圆柱体上总的阻力，N；

H为三维圆柱体浸水深度，m。

表3 时均阻力系数计算结果

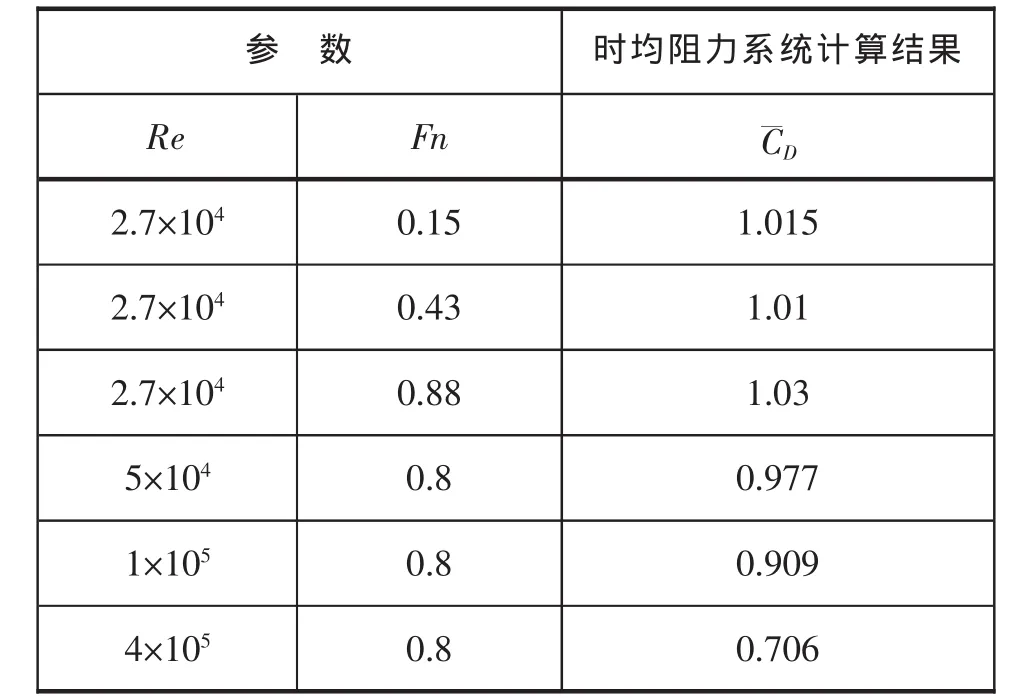
表3 时均阻力系数计算结果

参 数 时均阻力系统计算结果Re Fn C¯D 2.7×104 0.15 1.0152.7×104 0.43 1.012.7×104 0.88 1.035×104 0.8 0.9771×105 0.8 0.9094×105 0.8 0.706

圆柱各个截面的时均阻力系数可由式（4）计算得到:

式中:Cp为模型表面所受到的时均压力系数。

图9 不同截面时均阻力系数沿展向变化图

由图9可以发现，展向时均阻力的变化趋势非常明显，相同水深处的时均阻力系数随着雷诺数的增大而减小。时均阻力系数在自由液面处较小，接近于0；随着水深的增加，在水深为0.5D时，时均阻力系数突然增加，出现一个极大值；在Z/D＜-1时，随着水深继续增加，展向时均阻力系数逐渐减小。当Z/D=0时，各个工况的时均阻力系数比较接近，为0.32～0.4；在Z/D=-4处，Re=2.7×104、Fn=0.88时，时均阻力系数最大（约为0.93）；Re=4×105、Fn=0.8时，时均阻力系数最小（约为0.56）。这表明，在自由液面之下，当雷诺数越小，傅汝德数的增加将使自由液面的影响在深度方向增大；当雷诺数增大时，较深水深处得自由液面的影响则越小。

4 结 论

本文基于计算流体力学软件CFX，应用RNG k-ε湍流模型，结合VOF方法，模拟均匀流场中半沉浸三维圆柱穿透自由液面的运动，并在流场雷诺数Re为104～105、傅汝德数 Fn 为 0.15～0.88 的范围内，计算自由面圆柱绕流的相关水动力特性，得出以下结论:

（1）在自由液面流场中，当三维圆柱绕流的傅汝德数一定、雷诺数较小时，自由液面对流场的作用明显；当雷诺数较大时，自由液面对流场流动的扰动影响将变小。

（2）自由液面对流场的影响水深随着傅汝德数的增加而增加，而雷诺数的变化对相同水深的时均压力系数影响不大。

（3）三维圆柱总时均阻力系数随傅汝德数和雷诺数增加而减小；相同水深处各截面的时均阻力系数也随傅汝德数和雷诺数的增加而减小。

［1］陈伟，宗智.二维圆柱绕流的离散涡数值模拟［J］.舰船科学技术.2010（6）:58-64.

［2］王亚玲，刘应中，缪国平.圆柱绕流的三维数值模拟［J］.上海交通大学学报，2001，35（19）:1464-1469.

［3］Burger M，Schmehl R，Koch R，et al.DNS of Droplet-Vortex Interaction with a Karman Vortex Street［J］.Heat and Fliud Flow，2006（27）:181-191.

［4］Dong S，Karniadakis G E.DNS of Flow Past a Stationary and Oscillating Cylinder at Re=10000［J］.Journal of Fluids and Structures，2005（20）:519-531.

［5］Pontaza J P，Chen H C.Three-Dimensional Numerical Simulations of Circular Cylinders Undergoing two Degreeof-Freedom Vortex-Induced Vibrations［C］//Proceedings of the 25th International Conference on Offshore Mechanics and Arctic Engineering.Hamburg，Germany:［s.n.］，2006:1-4.

［6］Hay A D.Flow about Semi-Submerged Cylinders of Finite Length［R］.Princeton University Report，1947.

［7］Menter F，Sharkey P.Overview of Fluid-Structure Coupling in ANSYS-CFX［C］//Proceedings of the 25th International Conference on Offshore Mechanics and Arctic Engineering.Hamburg，Germany:［s.n.］，2006:3-6.

［8］张亮，李云波.流体力学［M］.哈尔滨:哈尔滨工程大学出版社，2001:140-159，209-210.

［9］詹昊，李万平.不同雷诺数下圆柱绕流仿真计算［J］.武汉理工大学学报，2008，30（12）:129-132.

［10］Lam K，Wang F H.Three-Dimensional Nature of Vortices in the Near Wake of a Wavy Cylinder［J］.Journal of Fluids and Structures，2004（19）:815-833.

［11］S Mayer.Large Eddy Simulation of a Flow Past a Free Surface Piercing Circular Cylinder［J］.Journal of Fluids Enginerring.2002（124）:57-64.

［12］林宗虎，李永光，卢家才，等.气液两相流涡脱落特性及工程应用［M］.北京:化学工业出版社，2001:6-15.