循环荷载作用下高强混凝土收缩徐变试验研究

唐云清，柯敏勇，刘海祥，陈 松

(1．南京水利科学研究院 水利部水工新材料工程技术中心，江苏 南京 210029;2．重庆市水库大坝安全监测中心，重庆 401147)

收缩徐变是高强混凝土材料的重要特性，会导致结构受力与变形随时间变化，对混凝土结构长期变形影响很大［1］．对于预应力混凝土结构，由于混凝土收缩和徐变，预应力会逐步减小，达不到预期的效果;在节段施工的大跨度预应力桥梁中，由于结构体系的转换，前期结构产生的徐变变形增量受到后期结构的约束，将在结构中产生徐变次内力和支座次反力［2］．变化荷载作为一种施工和运行过程中的活载，如温差荷载、水荷载和汽车荷载等，通常采用分项系数办法计入荷载组合，用以分析钢筋混凝土结构的承载能力极限状态和正常使用极限状态，但通常不考虑活载对混凝土徐变效应的影响．而事实上活载对结构变形和应力的影响从施工阶段就已经开始，如在节段施工的大跨度预应力连续箱梁桥中，挂篮前移、节段浇筑和预应力张拉等工况，造成前一节段箱梁截面应力的循环变化［3］;在运行过程中，汽车等交通荷载、日照温差效应造成的周期性变化;在大跨度预应力混凝土渡槽中，温差效应和水荷载也会造成渡槽结构应力的周期性变化［4］．这类循环荷载对应共同特点是以某一应力为中心，而产生一定幅度的应力周期性循环变化．为研究循环荷载作用对高强混凝土长期变形特性的影响，赵启林等［5］开展循环荷载作用下标准试件的徐变试验，表明在循环荷载作用下高强混凝土的徐变比恒载作用下偏大1～2倍，且对高强混凝土早期徐变影响较大，但对中后期的徐变影响不明显，徐变值随着循环荷载时间间隔的增大而减小［5］．而对于预应力钢筋混凝土构件在循环荷载作用下的徐变特性是否有类似规律值得深入研究．

为深入探讨循环荷载对高强混凝土徐变的影响，有必要开展循环荷载作用下的预应力高强混凝土梁的长期变形试验分析，可为分析循环荷载条件下高强混凝土的弹性模量和徐变系数提供试验资料，进而对比分析收缩徐变系数和现有收缩徐变模型计算值，以获取可供工程应用的徐变预测模型．

1 试验设计

高强混凝土各组分用量见表1，试验采用钢筋混凝土梁，设计截面尺寸为100 mm×200 mm，跨度为2 850 mm，混凝土各组分用量为:水泥482 kg/m3，水159 kg/m3，砂614 kg/m3，石1 150 kg/m3，水灰比为0．33，减水剂为水泥用量的0．7%．钢筋及预应力布置见图1，试验装置见图2，且混凝土表面不作密封处理．为方便比较，同时开展恒载作用下梁的徐变试验．

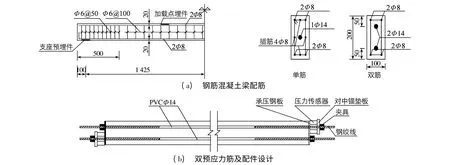
图1 钢筋混凝土梁配筋及预应力布置(单位:mm)Fig．1 Reinforcement and prestressed steel bars of concrete beams(unit:mm)

徐变试验加载通过梁体截面内对称张拉预应力和三分点加载实现，试验组合见表1，共有编号为A，B，C，D，E，F，G，H，K和L等10根梁，其中A和E梁为补偿普通钢筋混凝土．基准荷载分别为100，160和500 kg，荷载变化幅度分别为20，40和100 kg，相应试验梁应力状态变化见表1，初始加载龄期为7 d，3组梁加载周期同为4 d，每天变载1次，应力变化示意见图3;变形测量布置见图4，每天循环加载前后各测量1次，记录每天位移变化．试验总共设置10组，其中2组为测量自重徐变效应的补偿普通钢筋混凝土梁，3组纯弯徐变试验梁，包括2组恒载纯弯试验梁和1组纯弯循环加载试验梁;另设置了5组不同应力水平的压弯试验梁，包括3组恒载试验和2组循环荷载试验，试验组合见表1．根据试验需要，配套开展了高强混凝土棱柱体和立方体抗压强度、弹性模量等试验，结果见表2，得28 d混凝土立方体抗压强度为69．3 MPa，相应的棱柱体抗压强度为53．0 MPa．

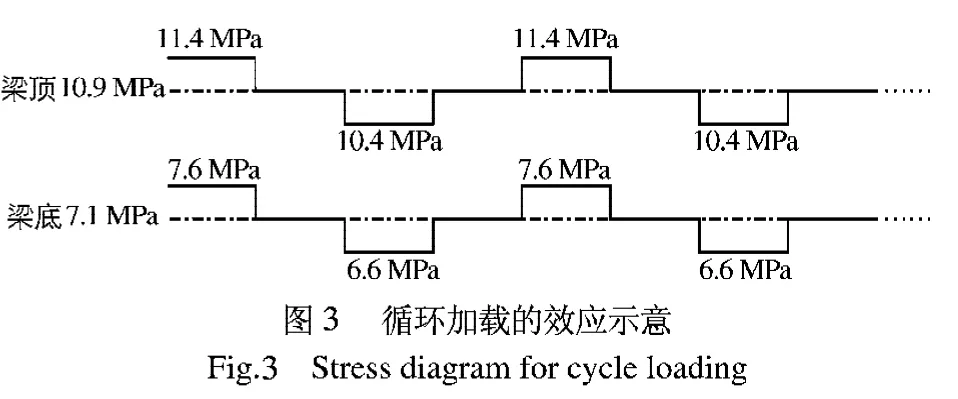
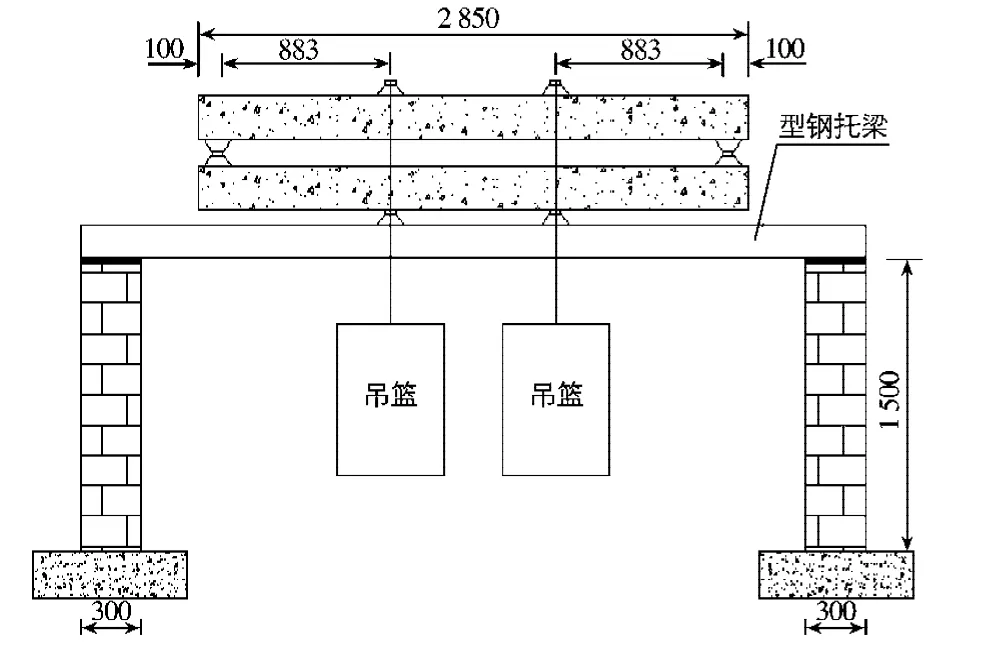
图2 加载试验装置(单位:mm) Fig．2 Layout of loading tests(unit:mm)

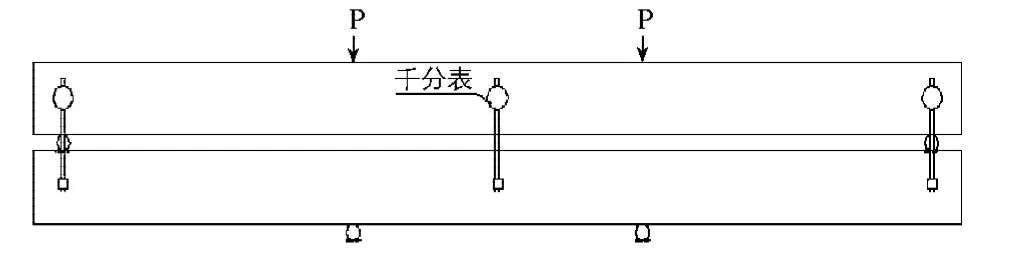
图4 挠度测点布置Fig．4 Deflection measurement

表1 试验用预应力钢筋混凝土梁应力状态组合Tab．1 Stress status of prestressed reinforced concrete beams

表2 混凝土力学性能试验结果Tab．2 Mechanical properties of concrete

2 试验结果分析

取梁两端简支点两侧共4只千分表和梁中两侧2只千分表的变形观测数据作分析．梁中相对位移按式(1)计算［6］:

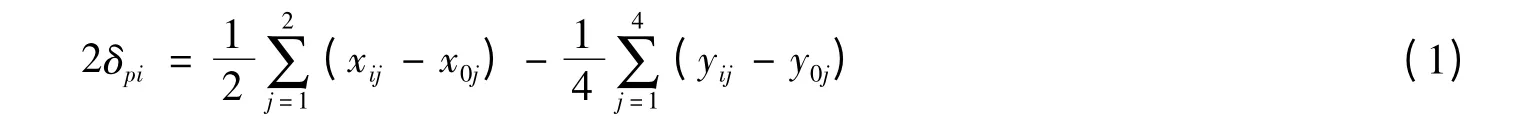
式中:δpi为第i天荷载对应的梁中挠度;xij为第i天荷载j号表的读数值，x0j为基准读数;yij为简支点上j号表第i天荷载的读数值，y0j为基准读数．

2．1 弹性特征分析

为研究循环荷载过程中梁的变形特征，计算循环加卸载过程中变形增量，以对比循环加卸载过程中的变形．通过计算加卸载过程中变形量的均方差，以2倍均方差为去异标准剔掉波动较大数据，再重新计算其平均值，结果见表3．

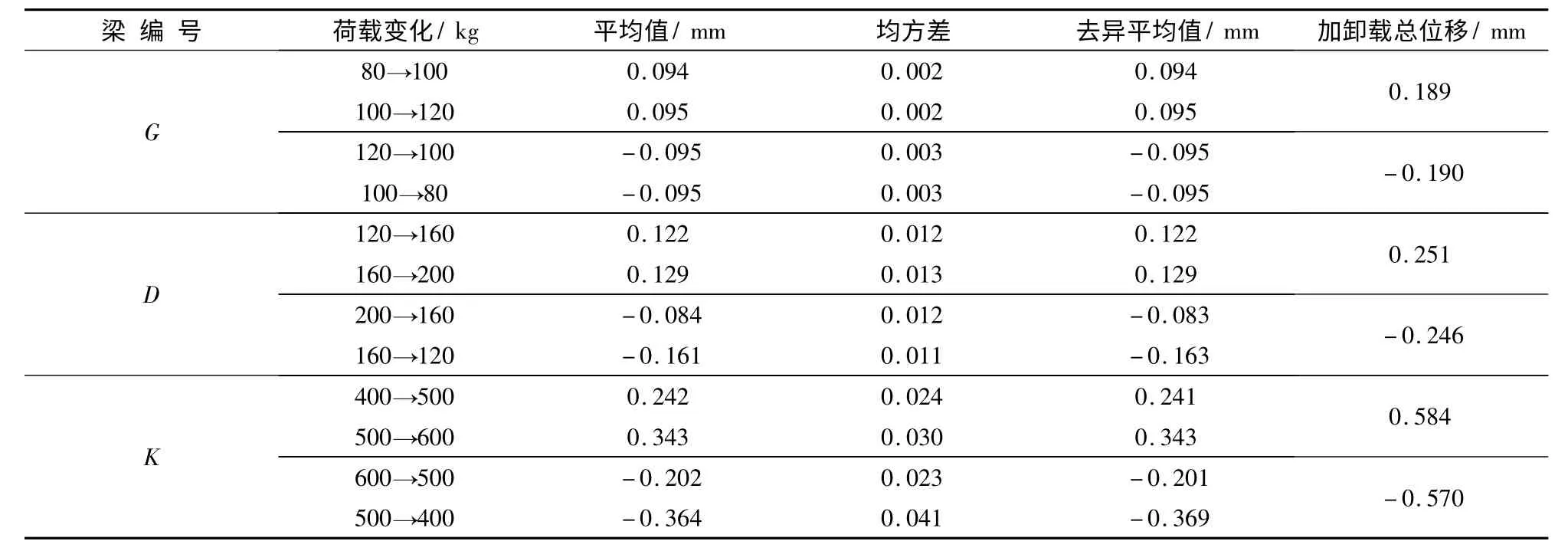
表3 循环加卸载作用下钢筋混凝土梁的弹性位移增量值Tab．3 Elastic displacement increment of RC beams with cycle loading and unloading

从表3可见，G梁加卸载过程中的变形量具有线弹性特性，加卸载变形量分别为0．095和0．094 mm，总变形量为0．189 mm;D梁在加载阶段具有线弹性特性，两级加载的变形量分别为0．122和0．129 mm;但卸载过程中有较大差异，从200 kg卸载到160 kg时为-0．084 mm，而从160 kg卸载到120 kg时为-0．161 mm;K梁则加卸载过程中均具有非线性特性，从400 kg加载到500 kg时的变形量为0．242 mm，从500 kg加载到600 kg为0．343 mm;在卸载阶段，从600 kg卸载到500 kg的变形量为-0．202 mm，从500 kg卸载到400 kg为-0．364 mm．

根据材料力学方法［7］，利用梁跨中的变形量δpi与荷载变化幅度ΔP，推算弹性模量为:

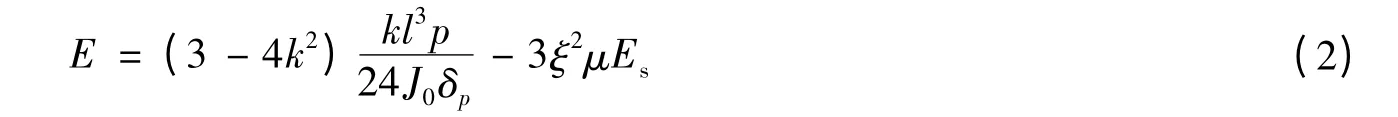
式中:J0为截面惯性矩;ξ为上下层钢筋距离h0与梁高h比h0/h;μ为上层或下层钢筋截面积As之2倍与截面积bh之比，即μ=2As/(bh);k为荷载作用点到简支点距离同梁长的比值，即为1/3．

再将有关参数值代入式(1)，经计算得式(3)，计算得到的弹性模量见表4．

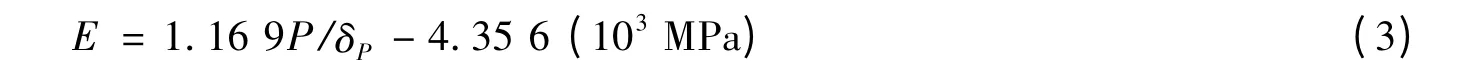
表4 弹性模量计算结果Tab．4 Calculated results of elastic modulus

由表4可见，在循环变化荷载作用后弹性模量有不同程度的提高，G梁加载和卸载的弹性模量分别提高了6．6%和6．1%;D梁则分别提高了56．5%和60．0%;K梁为61．4%和65．7%．导致该现象原因是，混凝土内部空隙在预应力作用下被压缩和减少，内部颗粒间压缩得更紧密，而循环荷载作用加剧了该趋势．

2．2 徐变分析

在获得钢筋混凝土长期变形观测结果后，采用有效模量法［1］和老化理论［8］建立钢筋混凝土徐变系数Φm与高强混凝土徐变系数Φ关系式，现设高强混凝土梁中的钢筋应力［6］为:

式中:M为梁中弯矩;

加载时刻的钢筋应力初始值为:

梁的钢筋应力与挠曲变形成正比，即有:

将式(4)和式(5)代入式(6)，并根据受弯徐变系数定义，得:

式(4)中第2式的μ数值较小，且28 d后弹性模量变化很小，可用n代替n(τ)，此时η成为:

再将式(7)代入式(8)消去η，得混凝土徐变系数推算式为:

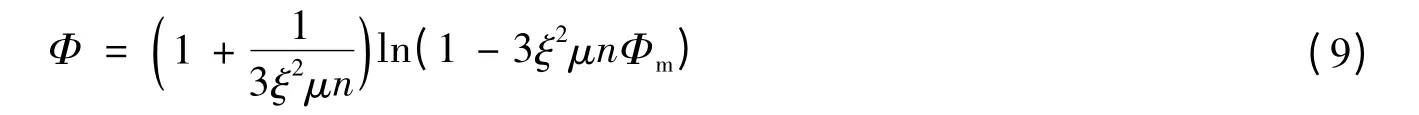
推导式(9)时混凝土的徐变物理方程采用了老化理论方程式，而采用有效模量法表示徐变物理方程时，可由钢筋应力计算式得到徐变系数Φm与混凝土徐变系数Φ关系:

式(10)经移项整理，可得:

最后将试验梁截面尺寸b，h，h0，As各数值代入式(11)，再将纯弯边缘应力σ0及初始应力σ代入压弯徐变系数计算式得到2个推算式，按老化理论推导得式(12):

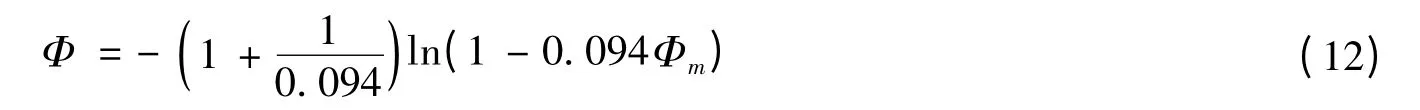
按有效模量法推导得式(13):

按上述2种方法计算结果取平均值后见表5．把循环荷载作用下的徐变测试结果和恒载徐变测试结果列于表6，结果表明:(1)恒载作用下相同单点荷载(如C，F，H梁)，轴向预应力越大徐变系数越小;(2)相同轴向预应力(如K，L梁及C，D梁)，循环荷载作用会增加混凝土的徐变系数;(3)相同轴压预应力(如K，H梁)，单点荷载作用越大徐变系数越大．

解释此试验现象可根据混凝土徐变的继效流动理论，循环荷载作用下造成梁体应力循环变化，即对高强混凝土不断实施加卸载，从而导致卸载后的可恢复徐变大幅减小．

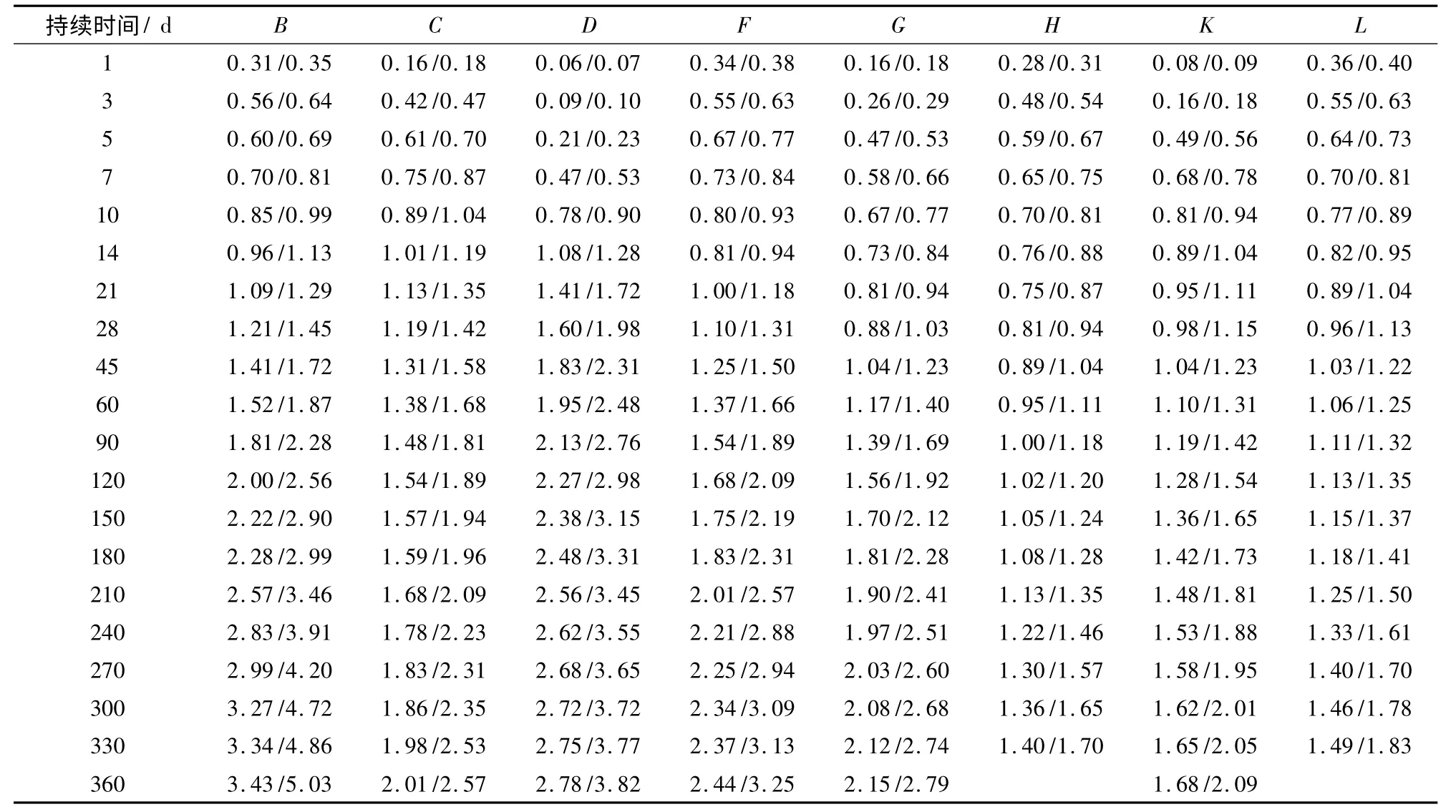
表5 钢筋混凝土试验梁及混凝土的徐变系数Tab．5 Creep coefficients of RCbeams and concrete

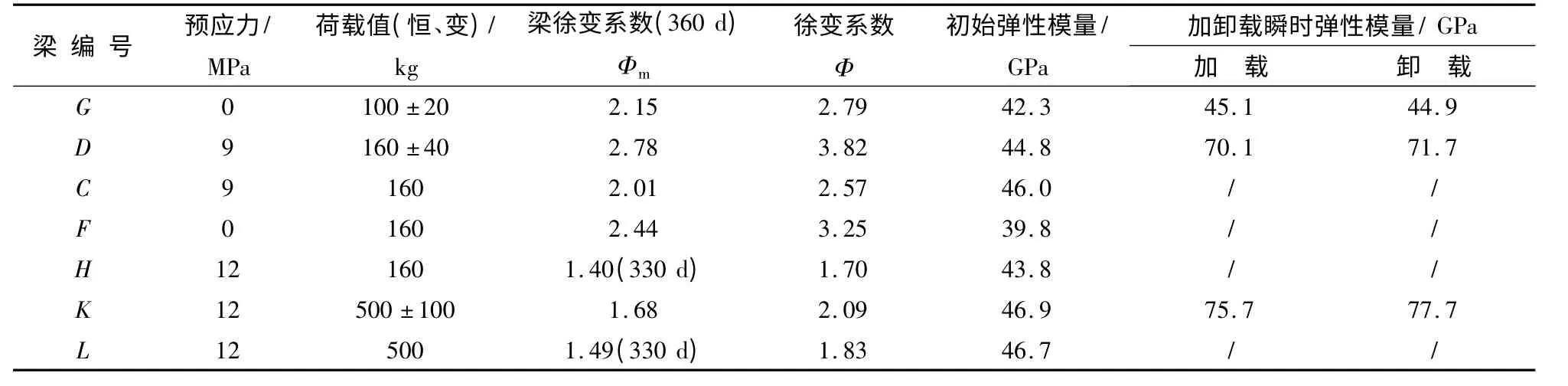
表6 试验梁徐变系数与弹性模量Tab．6 Elastic modulus and creep coefficients

2．3 与现有预测模型比较

现有预测混凝土徐变发展趋势的数学模型很多，但多为根据试验资料统计得出的经验公式，反映的是所统计混凝土的共性，而混凝土原材料成分和施工条件等造成的差异均难以在模型中体现，使得不同预测模型得出的结果相差很大［9］．

将本次试验结果和常用徐变计算模型ACI209［10］、CEB-FIP78［11］、CEB-FIP90［12］、B3［13-14］的计算结果进行比较，结果见图5，其中图5(a)表明采用常用计算模型不能预测D梁混凝土徐变发展规律，所有预测值均小于试验计算值;图5(b)表明G梁在前60 d左右的预测模型值大于G梁试验计算值，60 d以后G梁的徐变系数则介于B3模型和CEB-FIP78模型之间;图5(c)表明所有预测模型的徐变值均大于K梁试验计算值．可见，现有的预测模型不能很好地预测循环荷载作用下钢筋混凝土梁徐变发展规律，且循环荷载作用下混凝土徐变系数体现出很大的差异性，若统一运用现有模型来预测实际循环荷载作用下钢筋混凝土梁徐变系数会出现较大误差．薛伟辰等［15-16］研究表明预应力高性能混凝土梁长期变形的影响因素主要包括混凝土种类、预应力筋张拉方式、截面上下缘应力差等，认为梁体截面承受较大的应力差，徐变增长速度较快，由此而产生的混凝土徐变也相应较大．根据提供的经验式计算变形放大系数，则D梁长期变形放大系数为1．10，G梁为1．02，而K梁为1．40．由于放大系数的差异，造成了试验曲线和理论预测模型之间出现偏差．因此需要根据循环荷载梁轴向预应力及过程开展回归分析，得到混凝土徐变系数拟合式见(14):

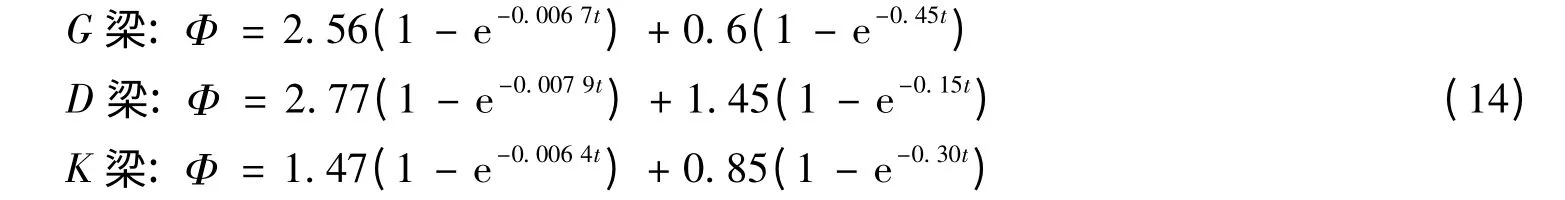
图6为拟合计算式和实验结果的比较，可见拟合计算式具有良好的拟合精度．

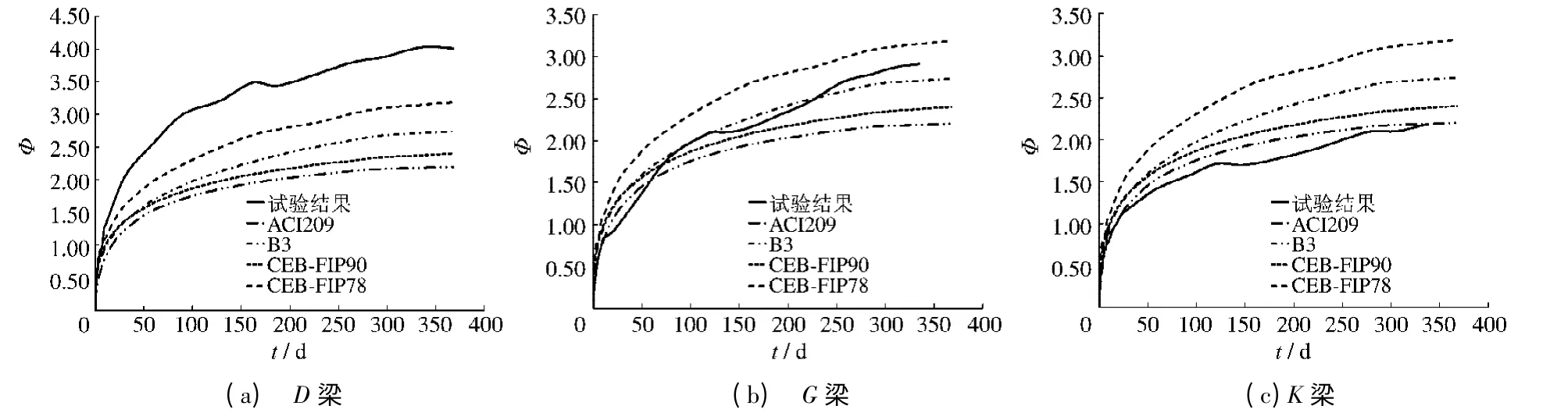
图5 各混凝土梁徐变系数试验值与常用模型计算值比较Fig．5 Comparison between creep coefficients and calculated values

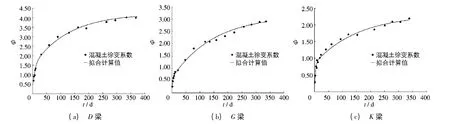
图6 徐变系数与拟合值比较Fig．6 Comparison between creep coefficients and simulated values

3 影响因素分析

3．1 预应力水平

降低纵向有效预应力对大跨度预应力连续箱梁桥长期变形性能有重要影响．如广东省佛开高速公路上大跨径连续梁桥汾江大桥［16］在桥面铺装刚结束后，各种预应力束和张拉应力的损失平均接近28%．对于成桥10 a后的挠度，预应力损失每增大5%，挠度会增大13．2%．按照《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG D 62-2004)计算，虽然预应力损失比《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTJ 023-85)计算结果略小，但平均为19．4%;预应力损失每增大5%，挠度会增大14．0%．由此可见两种规范方法计算的预应力损失对长期挠度的影响较一致，长期挠度相对于预应力损失成非线性增长关系．湖北黄石大桥［17］为跨度245 m的5跨连续刚构桥，经过7 a的运行，箱梁裂缝和主梁下挠成为该桥的主要病害，经研究分析表明，主梁正弯矩区底板和负弯矩区顶板纵向预应力有效性的降低，是造成主梁跨中持续下挠的主要原因之一．

在上述计算中通常不考虑预应力损失和混凝土徐变的耦合关系，即不考虑预应力改变对高强混凝土徐变系数的影响．循环荷载作用下，D梁与C，F，H梁在不同预应力作用下徐变系数比较见图7，结果表明预应力越大，混凝土徐变系数越小，即预应力作用具有明显减少钢筋混凝土梁长期变形的作用;而在循环荷载作用下，相同荷载时D梁徐变系数比C，F，H梁都要大，表明循环荷载加大了混凝土徐变系数，钢筋混凝土梁变形明显增加．结合该试验现象表明混凝土应力水平和大跨径预应力桥长期变形存在对应关系，即预应力损失和高强混凝土徐变进程具有耦合关系，预应力水平降低导致了高强混凝土徐变系数增大，徐变效应增大同时又导致了预应力水平进一步降低，耦合效应是导致大跨度预应力箱梁桥产生远超过设计预期变形的重要因素．

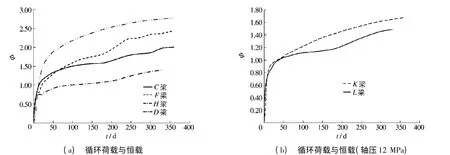
图7 循环荷载与恒载的徐变系数对比Fig．7 Creep coefficient comparison between the constant and the cycle loads

3．2 循环荷载和长期变形关系

循环荷载造成结构应力的周期性变化会不会造成结构变形的单调增加是值得关注的问题［18］．根据E．M．Wallo等试验［19］，当试验温度由4℃，21℃，43℃呈阶梯上升或由43℃，21℃，4℃呈阶梯下降时，徐变变形均为增加，其效果与应力分为3阶段按σ，2σ和3σ上升一致，试件在温度23℃加载35 d后，将室内的温度于23～60℃之间周期性反复进行分段升温及降温试验，徐变变形也单调增加，而且与相对湿度为50%的徐变相比，相对湿度为100%基本徐变的增加更为明显．将本试验结果和E．M．Wallo温度循环试验结果对照可发现，不管循环荷载是卸载或加载，结构应力周期性的增加或减少，高强混凝土的徐变发展均为单调递增．因此大跨度连续箱梁桥和刚构桥的长期变形过大与周期性循环荷载形成的徐变增加长期积累有关．

4 结语

通过本文研究，可得出以下主要结论:

(1)在3种应力水平下，随着循环荷载变幅增大，加卸载过程具备明显非线性特征，且弹性模量显著提高;在预应力和循环荷载作用下高强混凝土内部空隙减少，颗粒受到压缩是弹性模量提高的原因．

(2)在循环荷载作用下高强混凝土徐变系数较静载作用增加明显，源于循环荷载作用下梁体不断实施加卸载，从而导致卸载后可恢复徐变大幅减小;应用现有徐变预测模型预测循环荷载作用下混凝土徐变系数偏差较大．建议采用指数函数模型，可得到拟合精度较高的徐变系数拟合式．

(3)循环荷载作用下高强混凝土徐变发展呈单调递增性，预应力损失和徐变进程具有耦合关系，预应力水平降低导致了徐变系数增大，徐变效应增大又促进了预应力水平的进一步降低．

(4)由于试验组次限制，本次试验结果尚须进一步论证和深入研究，以期弄清循环荷载幅度、加载龄期和周期对徐变影响的规律．

［1］惠荣炎，黄国兴，易冰若．混凝土的徐变［M］．北京:中国铁道出版社，1988:50-51．(HUIRong-yan，HUANGGuo-xing，YI Bing-ruo．Concrete creep［M］．Beijing:China Railway Publishing House，1988:50-51．(in Chinese))

［2］胡狄．预应力混凝土桥梁徐变效应分析［D］．长沙:中南大学，2003．(HU Di．Analysis of creep effect in prestressed concrete bridges［D］．Changsha:Central South University，2003．(in Chinese))

［3］谭皓，刘钊．大跨度连续刚构桥徐变挠度影响因素分析［C］∥中国土木工程学会桥梁与结构工程分会．第十七届全国桥梁学术会议论文集，北京:人民交通出版社，2006:1073-1077．(TAN Hao，LIU Zhao．Deformation influence analysis for continuous rigid frame for long span bridges［C］∥Bridge and Structural Engineering Branch of China Civil Engineering Society．the Proceedings of 17thBridge Engineering，Beijing:China Communications Press，2006:1073-1077．(in Chinese))

［4］吴泽玉，李玉河，白新理．渡槽前水体温度的有限元计算［J］．人民长江，2008(3):50-53．(WU Ze-yu，LI Yu-he，BAI Xin-li．FEM analysis of water temperature before flume［J］．Yangtze River，2008(3):50-53．(in Chinese))

［5］赵启林，陈立，翟可为．复杂状态下桥用高强混凝土收缩徐变性能试验［J］．解放军理工大学学报:自然科学版，2011，12(5):459-466．(ZHAO Qi-lin，CHEN Li，ZAI Ke-wei．Creep and shrinkage of high strength concrete for bridges under complex condition［J］．Journal of PLA University of Science and Technology(Natural Science Edition)，2011，12(5):459-466．(in Chinese))

［6］陈松．混凝土徐变过程数值分析及试验研究［D］．南京:南京水利科学研究院，2009．(CHEN Song．Numerical analysis and experiments for high strength concrete creep［D］．Nanjing:Nanjing Hydraulic Research Institute，2009．(in Chinese))

［7］陈灿明，黄卫兰，唐崇钊．南水北调工程高性能混凝土长期变形特性［R］．南京:南京水利科学研究院，2008．(CHEN Can-ming，HUANG Wei-lan，TANG Chong-zhao．Long term deformation of high performance concrete in South-to-North Water Diversion Project［R］．Nanjing:Nanjing Hydraulic Research Institute，2008．(in Chinese))

［8］柯敏勇，刘海祥，陈松．桥用高强混凝土双轴徐变试验研究［J］．建筑结构学报，2012，33(6):16-22．(KE Min-yong，LIU Hai-xiang，CHEN Song．Bixial creep experiment for high strength concrete in bridge engineering［J］．Journal of Building Structures，2012，33(6):16-22．(in Chinese))

［9］ZDENEK PBAŽANT，LISA PANULA．Creep and shrinkage characterization for analyzing prestressed concrete structures［J］．Journal of the Prestressed Concrete Institute，1980，25(3):86-122．

［10］ACI 209R-92，Prediction of creep，shrinkage，and temperature effects in concrete structures［S］．

［11］CEB-FIP:Model code for concrete structures［S］．

［12］CEB-FIPmodel code 1990，Design code［S］．

［13］BAZANT Z P，BAWEJA S．Creep and shrinkage prediction model for analysis and design of concrete structures-model B3，RILEM recommendation［J］．Materials and Structures，1995，28(3):357-365．

［14］王巍．轨道交通预应力混凝土梁长期性能试验与理论研究［D］．上海:同济大学，2006．(WANG Wei．Experimental and theoretical studies on long term behaviors of prestressed concrete beams for rail transportation［D］．Shanghai:Tongji University，2006．(in Chinese))

［15］薛伟辰，胡于明，王巍，等．1200 d预应力高性能混凝土梁长期性能试验研究［J］．同济大学学报:自然科学版．2008，36(8):1018-1023．(XUE Wei-chen，HU Yu-ming，WANG Wei．Experimental study on long term behavior of prestressed HPC Beams for 1 200 days［J］．Journal of Tongji University(Natural Science)，2008，36(8):1018-1023．(in Chinese))

［16］石雪飞，陈辉，沈炯伟．已下挠连续梁桥加固方案研究［J］．石家庄铁道学院学报:自然科学版，2010，23(1):1-5．(SHI Xue-fei，CHEN Hui，SHEN Jiong-wei．Study on reinforcement of deflected continuous beam bridge［J］．Journal of Shijiazhuang Railway Institute(Natural Science)，2010，23(1):1-5．(in Chinese))

［17］詹建辉，陈卉．特大跨度连续刚构主梁下挠及箱梁裂缝成因分析［J］．中外公路，2005，25(2):56-58．(ZHAN Jianhui，CHEN Hui．The deflection and reason analysis of concrete crack of main box beam for large span continuous rigid frame bridge［J］．Journal of China＆Foreign Highway，2005，25(2):56-58．(in Chinese))

［18］陈灿明，黄卫兰，陆采荣，等．桥用高性能混凝土的徐变与应用［J］．水利水运工程学报，2007(2):1-9．(CHEN Canming，HUANG Wei-lan，LU Cai-rong，et al．Creep of high-performance concrete for bridges and its application［J］．Hydro-Science and Engineering，2007(2):1-9．(in Chinese))

［19］WALLO E M，KESLER C E．Prediction of creep in structural concrete，Bulletin 498［R］．Chicago:University of Illinois Engineering Experiment Station，1966．