探测窗口的NAFω算法
蒋洪波,冯新宇,栾 兵,沈显庆
(1.黑龙江科技学院 黑龙江 哈尔滨 150027;2.东北农业大学 成栋学院,黑龙江 哈尔滨 150025)
椭圆曲线自引入密码学以来一直备受人们青睐,它的突出特点吸引着密码爱好者们对它的不断探索和研究,随着计算能力的增强对其实现速度也提出了更高的要求,关于实现速度的研究大部分集中在影响加密速度的几个关键点上,其中椭圆曲线上的点乘运算是研究热点之一,而研究点乘又主要集中在NAF标量乘[1]上,它们大都是将NAF算法与其他算法结合实现,没有从NAF算法本身出发提高速度,而本文则是立足NAF算法进行分析研究。在NAF算法中若NAF的长度为,那么算法中的移位运算就要进行次,该移位运算消耗了大部分的算法时间。本文提出的探测窗口法实现NAF则大大减少了算法中的移位次数,为所有基于NAF的算法提高了运算效率。该算法简单便于实现,实现效率高。
1 窗口宽度ω的AFω算法
假设实现平台的字长是W位,并且W是8的整数倍。则字U的W位,分别以W-1到0标记,且第W-1位为最高有效位。
设 f(z)是一个,次的二进制既约多项式,记做 f(z)=zm+r(z),则GF(2m)上的元素是次数最多为m-1的二进制多项式。
一个域元素a(z)=am-1zm-1+…+a2z2+a1z+a0与一个m维向量 a=(am-1,…,a2,a1,a0)相对应。 令 s=[m/W],t=Ws-m。 软件实现时 k 用 s个 W 字的一个数组 K=(K[s-1],…,K[1],K[0])来存储,最低有效位k0存储到K[0]中,并且K[s-1]的最左t位没有用(总是设置为0)。
因为域元素的移位是整体移位,因此总共只需要个s字的移位。
椭圆曲线点乘运算中,若允许利用额外的存储器和预计算,那么用加减法实现点乘可以获得更高效的点乘算法,把它叫做计算点乘的窗口方法[2]。
1.1 非相邻表示型
椭圆曲线点乘算法中需要先计算 NAF(k)或 NAFω(k),其中NAF称作非相邻表示型。
设 P=(x,y)∈E(Fq)。若 Fq是二进制域,则-P=(x,x+y);若Fq的特征大于 3,则-P=(x,-y)。 因此椭圆曲线的点的减法与点的加法一样有效。它促使我们使用k的带符号数字表示

这种特别带符号数字表示就是非相邻表示型。
定理1(的性质)令是一个正整数。
1)k 有惟一的 NAF,并记为 NAF(k)。
2)NAF(k)在k的所有带符号表示中具有最少的非零位。
3)NAF(k)的长度最多比k的二进制表示的长度大1。
4)若 NAF(k)的长度是 l,则 2l/3<k<2l+1/3。
5)所有长度为l的NAF中非零数字的平均密度约为1/3。利用算法1可以有效地计算NAF(k)。
算法1计算一个正整数的NAF
输入:一个正整数k。
输出:NAF(k)。
1)i=0。
2)当 k≥1 时,重复执行
若k是奇数,
则 ki=2-(k mod4),k=k-ki。
否则,ki=0。
k=k/2,i=i+1
3)返回(ki-1,ki-2,…,k1,k0)。
NAF(k)的各位数字可通过连续用2去除k且允许余数取 0 或±1 来得到。 若 k 是奇数,则余数 r∈{-1,1},以使商(k-r)/2是偶数,这将确保下一个NAF数字是0。
1.2 窗口宽度的
宽度为ω的NAF记为:
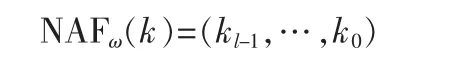
定义2令ω≥2,那么每一个正整数k都有惟一的宽度为ω的NAF表达式:

其中非零系数 ki都是奇数,|ki|<2ω-1,kl-1≠0,且任意连续 ω个数字中最多有1位为非零。宽度为ω的NAF的长度是l[3]。
定理2(宽度ω的NAF的性质)令k是一个正整数。
1)k 有惟一的宽度 ω 的 NAF,并记为 NAfω(k)。
2)NAF2(k)=NAF(k)。
3)NAFω(k)的长度最多比k的二进制表示的长度大1。
4)所有长度为l的宽度ω的NAF中,平均非零数字的密度约为 1/(ω+1)。
整数k在计算机中都以二进制形式存放,因此若令k=987 654 321,那么k的二进制表示为:

算法2计算一个正整数窗口宽度为ω的NAF算法
输入:一个正整数k。
输出:非相邻表示型 NAFω(k)
1)c←k
2)s←<>
3)当 c>0,重复执行
如果c是奇数
那么 u←c mod2ω
c←c-u
否则u←0
在S中将u追加在前
c=c/2
4)返回 S
这里 c mod2ω表示一个正整数 u,u 满足 u≡c(mod2ω)且-2ω-1≤u≤2ω-1。
NAFω(k)的各位数字通过c连续除以2并使余数 r在区间[-2ω-1,2ω-1-1]内来获得。
2 探测窗口的算法
用算法 2可以计算 NAFω(k),若如上例所示 k=987 654 321,则用算法2计算ω分别为3、4、5和6时的NAF如下:

从中可以看出若k是奇数并且余数 r=k mod2ω,则(k-r)/2将能被2ω-1整除,从而使后面的ω-1个数字均为零[3]。因此可以将k←k/2改写为k←k/2ω,即把k一次向右移动1位改为 k 一次向右移动 ω 位。 与此同时将 ki+1,ki+2,…,ki+ω-1均赋值为0。
算法2采用从右向左的顺序进行运算。在k向右移动ω位之前为了避免在ω+1位、ω+2位、位之后还有多个零出现,因此提出了用宽度为1的小窗口w来向左探测后方是否还有零的出现,若探测窗口值为零,则将相应的值置0,并且窗口w向左移动1位继续探测是否还有0的存在。这种移动探测一直进行到探测窗口值等于1为止,此时先将k向右移位到窗口所在的位置,然后再进行相应的计算。探测窗口工作原理如图1所示。

图1 探测窗口原理图Fig.1 Schematic of detection window
图1中若ω=4且当前计算完ki-3的值,则可以直接将ki-1、和ki的值置0,探测窗口w从ai+1开始取值判断该位是否为0。若探测窗口w为0,则ki=0,探测窗口w继续向左移动一位,并且判断该位的值,值若为0,则ki+1=0,探测窗口w继续向左移动一位,重复上述判断和窗口移动的过程;值若为1,则将k向右移动ω+窗口移动次数位,然后再计算ki+1的值。计算完ki+1之后的处理过程和计算完ki-3之后的过程相同,如此往复循环下去,直至k=0为止,算法结束。
经过上述分析提出了如算法3所示的探测窗口的NAFω(k)算法。
算法3计算一个正整数的探测窗口的NAFω
输入:一个正整数k,窗口宽度ω。
输出:非相邻表示型 NAFω(k)
1)i←0。
2)窗口w取的最低位。
3)当 k≥1 时,重复执行
若探测窗口 w=0,则 ki←0,i←i+1,窗口 w 左移 1位。
否则,k右移到窗口w所在位置,
ki←k mod2ω,
k←k-ki,
将 ki+1,ki+2,…,ki+ω-1均赋值为 0,
i←i+ω,窗口w取第ω位的 k值。
4)返回(ki-1,ki-2,…,k1,k0)
其中k mod2ω与算法1中的c mod2ω含义相同。
3 实验结果及分析
算法2和算法3中的整数k在计算机中都是以二进制形式存放,因此算法中的k除以2等同于k向右移动1位,而k除以2ω等同于k向右移动ω位,本算法的时间复杂度可以用占用时间最多的移位运算来衡量[4]。
设 NAF的长度为 l,则算法 2需要 l(2s-1)次字移位,需要l(s-1)次字异或。在窗口宽度ω的NAF中,非零元素的平均密度近似为 1/(ω+1)[5],零元素的平均密度为 ω/(ω+1)[6],以平均密度来看,一位非零元素到下一位非零元素共间隔ω个零,因此算法 3 中共需要移位 l(2s-1)/(ω+1)次,异或 l(s-1)/(ω+1)次。
在域 GF(2283)上用 C对算法2和算法3建模,用 gcc在linux平台下编译仿真,进行多组随机数据验证,得到如表1所示的实验结果。
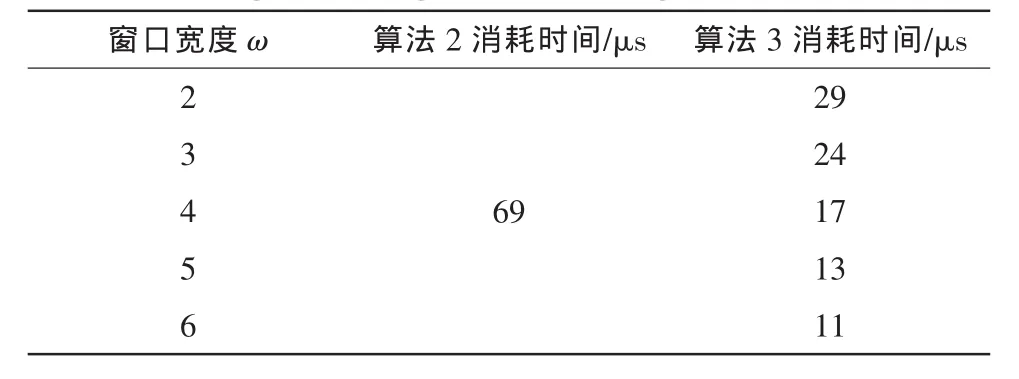
表1 m=283时算法2和算法3运行时间比较Tab.1 Running time of algorithm 2 and algorithm 3 when m=283
表1中的运行时间为算法关键部分的运行时间,即循环部分的运行时间。该仿真在W=32的平台上完成,所以每次算法中的移位需要由移位运算和异或运算共同来完成,且m=283,因此s=9,则每次移位需要17个字移位,每次异或需要8次字异或。
算法3与算法2相比其中的移位次数有了明显的减少,但是相对增加了探测窗口移动的运算,探测窗口移动的时间消耗为一个字的按位与,而算法中的一次移位操作需要2s-1个字的移位和s-1个字的异或,从总体上来看,一次探测窗口移动的时间要远远小于算法中的一次移位,即不会影响整个算法的时间复杂度。
算法2与算法3在不同ω值时的时间消耗曲线如图2所示。
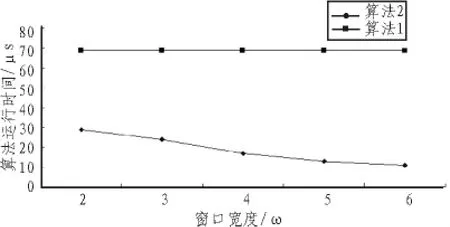
图2 当取不同值时算法2和算法3的时间曲线Fig.2 Time curve of algorithm 2 and algorithm 3 when ω is deffrent
4 结束语
本文对文献[2]提出的NAFω算法进行了分析和研究,根据其特点提出了探测窗口的NAFω算法,该算法大大减少了原始算法的移位次数,经理论分析和建模仿真验证,该算法的时间消耗约为算法2的1/(ω+1)倍,且随ω的增大运算效率也在提高,探测窗口的NAFω算法为快速实现椭圆曲线上的点乘运算和其他基于NAF的运算奠定了基础。
[1]沈学利,张龙华,姜丽.NAF标量乘算法的改进 [J].计算机仿真,2010,27(2):316-319.
SHEN Xue-li,ZHANG Long-hua,JIANG Li.Improvement of NAF scalar multiplication algorithm[J].Computer Simulation,2010,27(2):316-319.
[2]JEROME A.SOLINAS.Efficient Arithmetic on Koblitz Curves[J].Designs, Codes and Cryptography,2000 (19):195-249.
[3]Darrel H,Alfred M,Scott V.椭圆曲线密码学导论[M].张焕国,译.北京:电子工业出版社,2005:92-95.
[4]Gordon D M.A survey of fast exponentiation methods[J].Journal of Algorithms,1998,27(1):129-146.
[5]Morain F,Olivos J.Speeding up the Computations on an Elliptic Curve using Addition-subtraction Chains[J].Informatique Théorique et Applications,1990(24):531-544.
[6]瞿云云,包小敏.模幂运算的窗口NAF方法[J].西南大学学报:自然科学版,2009,31(9):60-64.
QU Yun-yun,BAO Xiao-min.A window NAF algorithm for modular exponentiation[J].Journal of Southwest University:Natural Science Edition,2009,31(9):60-64.

