The Boussinesq方程新的精确解
张亚敏
(宝鸡文理学院 数学系,陕西 宝鸡 721013)
随着科技的迅速发展,非线性方程已被广泛的应用到众多领域中,如光学、流体力学、电磁波等,从而出现了许多求解非线性微分方程的方法,主要有逆散射法[1]、Hirota双线性法[2]、齐次平衡法[3]、Backlund 变换法[4]等。 近些年,由于计算机代数与符号计算的发展,人们发现求解非线性方程许多新的方法[5],如齐次平衡法[6-7]、双曲函数法、几何方法等。
本文采用F—展开法,借助一种改进的辅助函数的解,并结合符号计算,运用Maple环境中的Epsilon软件包,求解the Boussinesq方程[8]得到了若干其他方法不曾给出的,形式更为丰富的新的显示行波解,其中包括双曲函数解和三角函数解。
1 The Bouqssinesq方程新的解
求解the Boussinesq方程
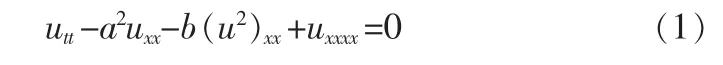
为求方程(1)新的行波解,令
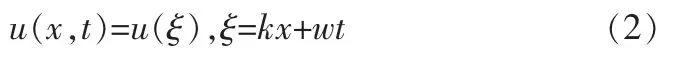
将(2)式代入(1)式,并积分两次得
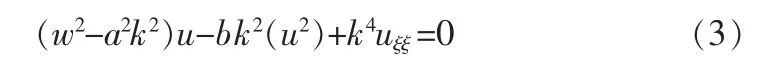
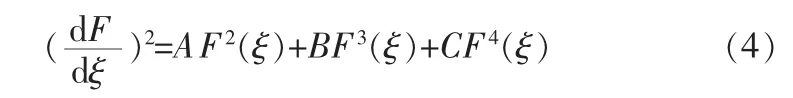
由平衡法得u=2,则

将(5)式代入(3)式,并根据(4)式得到关于 F(ξ)的函数,令F(ξ)各次幂的系数为0,得如下方程组:
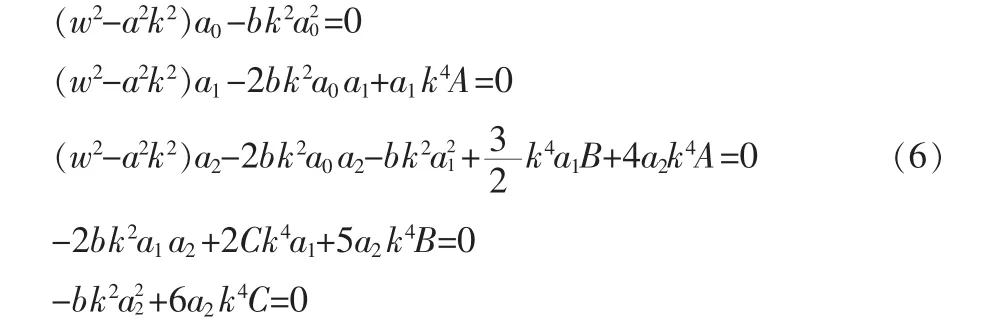
利用Maple求解上面方程组,得
1)在 A>0,C 为任意数时,则方程(1)的解为
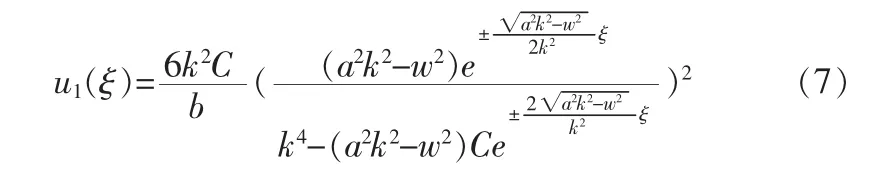
2)在 A>0,Δ=B2-4AC>0 时,即 C<0,方程(1)的解为
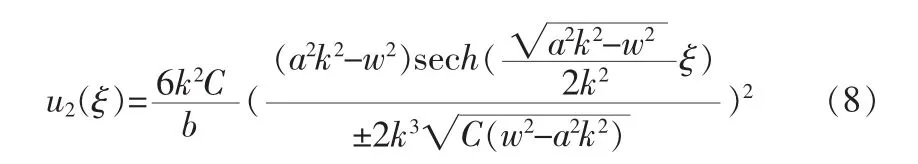
3)在 A>0,Δ=B2-4AC<0 时,即 C>0,方程(1)的解为
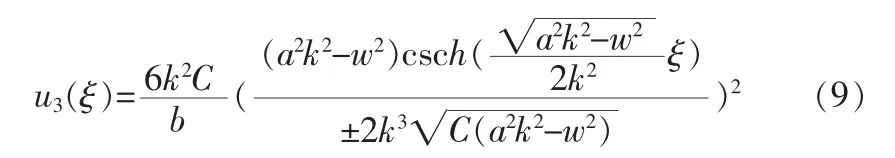
4)在 A<0,Δ=B2-4AC>0 时,即 C>0,方程(1)的解为
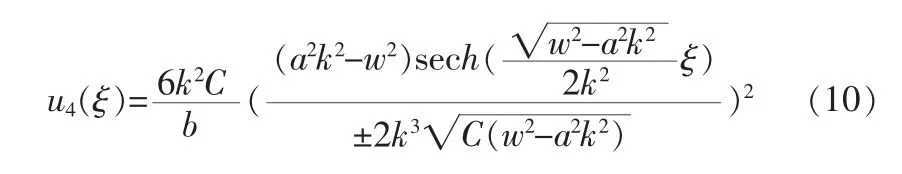
5)在 A<0,Δ=B2-4AC<0 时,即 C<0,方程(1)的解为
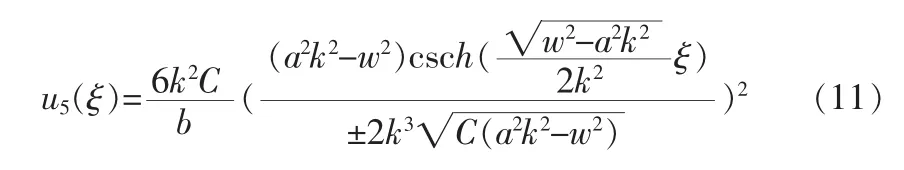
1)在 A>0,方程(1)的解为
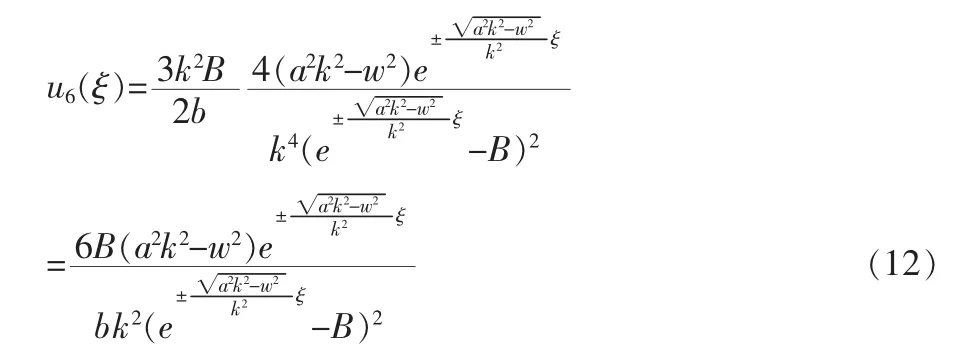
2)在 A<0,方程(1)的解为
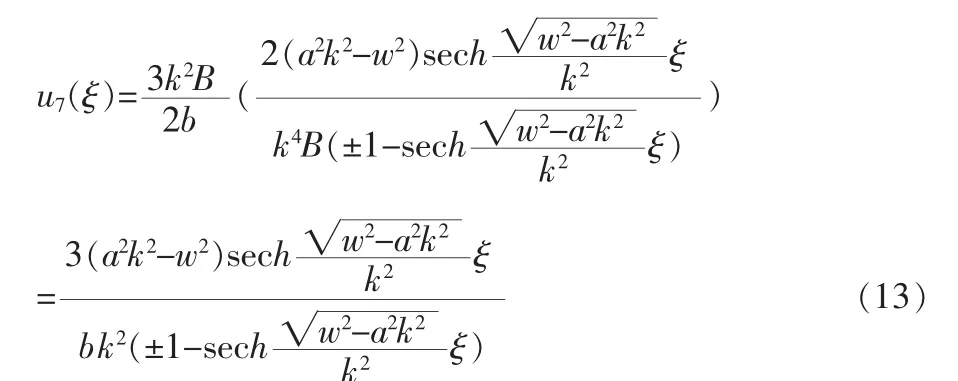
1)在 A>0,C 为任意数,方程(1)的解为

2)在 A>0,Δ=B2-4AC>0 时,即 C<0,方程(1)的解为
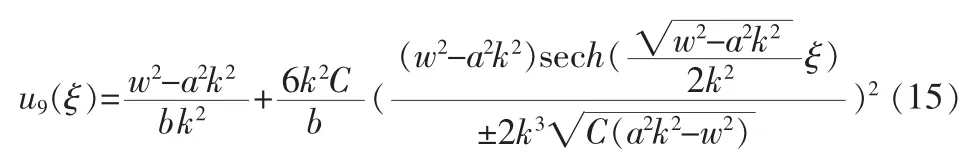
3)在 A>0,Δ=B2-4AC<0 时,即 C>0,方程(1)的解为
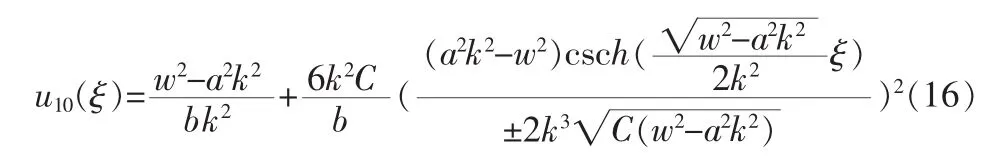
4)在 A<0,Δ=B2-4AC<0 时,即 C>0,方程(1)的解为
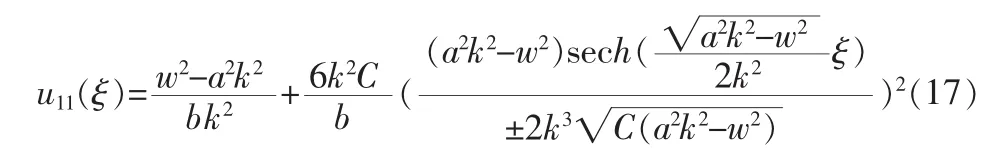
5)在 A<0,Δ=B2-4AC<0 时,即 C<0,方程(1)的解为
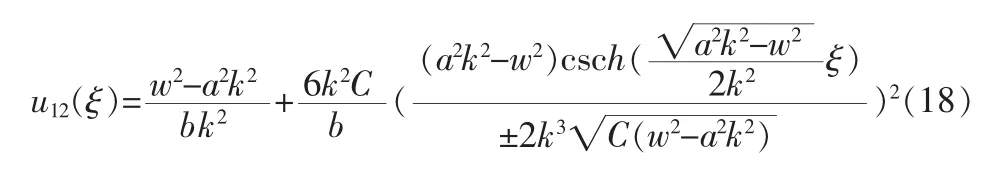
1)A>0,方程(1)的解为
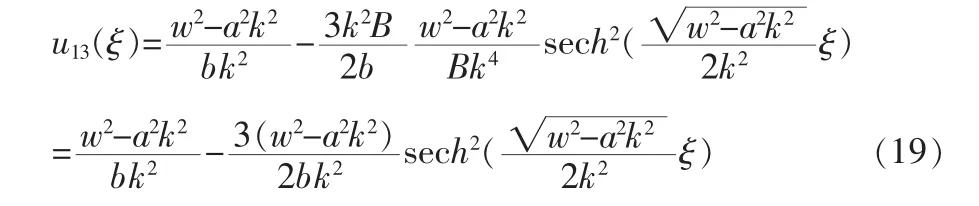
2)A<0,方程(1)的解为
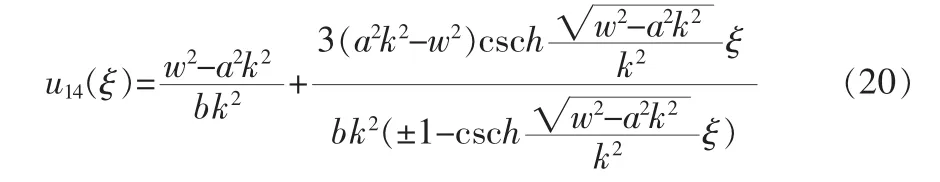
2 结束语
本文利用一种改进的辅助函数法,并运用Maple环境中的Epsilon软件包,求解the Boussinesq方程,获得了若干其它方法不曾给出的新的精确解,运用此方法可以求出许多方程新的精确解。
[1]Gardner C S,Greene J M,Kruskal M D,et al.Method for solving the Kortewege-de Vries equation[J].Physical Review Letters,1967(19):1095-1907.
[2]Hirota R.Exact solution of the Korteweg-de vries equation formultiple collisions ofsolitions[J].PhysicalReview Letters,1971(27):1192-1194.
[3]Senthilvelan M.On the extented applications of homogeneous balance method[J].Applied Mathematics and Computation,2001(123):381-388.
[4]Lamb G L.Backlund transformations for certain nonliear evolution equations[J].Journal of Mathematical Physics,1974(15):2157-2165.
[5]Zhang A E.A note on the homogeneous balance method[J].Physical Letters A,1998(246):403-406.
[6]李志斌,张善卿.非线性波方程准确孤立波解的符号计算[J].数学物理学报,1997,17(1):81-89.
LI Zhi-bing,ZHANG Shan-qing.Nonlinear wave equation accurately solitary wave solutions of symbolic computation[J].Journal of Mathematical Physics,1997,17(1):81-89.
[7]李德亮,韩安明.柔性机械臂有限时间控制器设计与仿真实现[J].现代电子技术,2012(14):106-108,112.
LI De-liang,HAN An-ming.Design and simulation of finitetime controller for flexible manipulators[J].Modern Electronic Technique,2012(14):106-108,112.
[8]Yan Z.Constructing exact solutions for two-dimensional nonlinear dispersion Boussinesq eqution[J].Journalof Mathematical Physics,2003,18(4):869-80.

