强酸性阳离子交换纤维吸附铟的热力学

李明愉，曾庆轩，李建博，冯长根

(北京理工大学 爆炸科学与技术国家重点实验室，北京 100081)

强酸性阳离子交换纤维吸附铟的热力学

李明愉，曾庆轩，李建博，冯长根

(北京理工大学 爆炸科学与技术国家重点实验室，北京 100081)

采用自制强酸性阳离子交换纤维对水溶液中In3+的吸附特性进行研究，在温度为293～323 K和研究的浓度范围内，强酸性阳离子交换纤维对In3+吸附平衡数据采用Langmuir、Dubini-Radushkevieh(D-R)、Freundlich、Temkin、Redlich-Peterson(R-P)和Koble-Corrigan(K-C)等6种等温吸附模型，对在不同温度下SACEF吸附In3+的等温实验数据进行线性和非线性拟合。结果表明：除Langmuir非线性拟合及Dubini-Radushkevieh模型之外，其余模型的线性及非线性拟合结果均较好，可以用于描述强酸性阳离子交换纤维吸附水中In3+的等温吸附行为，相关系数R2值都在0.9左右。综合考虑相关系数来看，Langmuir模型(线性拟合)最为适合。等量吸附焓表明：强酸性阳离子交换纤维对In3+吸附是吸热过程，水合In3+离子在强酸性阳离子交换纤维上的吸附焓大于0，是一个吸热、自发和熵增的过程，并对吸附行为进行了合理解释。

强酸性阳离子交换纤维；In3+；等温吸附模型；吸附热力学

铟是一种稀散金属，是电子、电信与光电产业不可缺少的关键材料之一，铟的用途主要集中在半导体、透明导电涂层、电子器件、荧光材料、金属有机物等方面。目前，全球铟的生产包括原生铟和再生铟两部分，再生铟又称回收铟，属铟资源的二次回收利用。2005年[1]，全球铟的消耗量大约为1 000～1 100 t，其中再生铟约为500 t，其余为原生铟。而1991年，全球铟的消耗量仅为133 t，由此可见，全球铟消耗量15年增长了8倍。我国铟出口占世界市场50%以上，铟在地壳中的丰度特别低，仅为0.1 μg/g，铟多数与其性质类似的锌、铅、铜和锡等共生[2]。由于稀散金属离子在化学性质上有许多相似之处，因此，稀散金属离子在分离、富集、回收方面困难较多。近年来，随着铟需求量不断增加，对于铟的富集、回收进行了很多的研究。目前，工业上传统的富集和回收铟的方法是溶剂萃取法，但是采用传统的方法来富集和回收铟具有很多不足之处，比如用P204作为萃取剂时，反萃取难、萃取剂易老化、循环利用能力差、萃取过程中容易乳化，造成了资源浪费，工业成本太高，难以广泛应用于工业生产[3]。

离子交换纤维可一次或多次使用，因此在贵金属、稀土元素及放射元素的提取和分离上具有独特的优势。从矿渣浸提液、矿水等稀溶液中回收金属效果很好。关于强酸性离子交换纤维(Strong acidic cationic exchange fiber，SACEF)的吸附In3+的热力学研究未见文献报道。本文作者用自制苯乙烯系聚丙烯基强酸性离子交换纤维[4]对水溶液中的In3+的吸附热力学性能进行研究，以期得到离子交换纤维吸附金属离子In3+的有关规律和热力学参数。为湿法冶金中In3+的分离和回收利用提供一种新的可能的途径。

1 等温吸附模型

1.1 Langmuir吸附等温模型

1916年，LANGMUIR首先提出单分子层吸附模型[5]。LANGMUIR假设的是一种理想的吸附过程，每一个吸附点的能量不变；吸附是均匀的单分子层吸附；动态平衡时，吸附和脱附速率相等。推导出平衡吸附量qe与溶液平衡浓度ce之间的关系为

转化成线性形式为

式中：eρ代表平衡浓度，mg/L；qe表示单位质量吸附剂的平衡吸附量，mg/g；qm是饱和吸附量，mg/g；KL是与结合能有关的系数，L/mg。

1.2 Dubinin-Radushkevieh(D-R)等温模型

Dubinin-Radushkevich吸附模型[6]描述的也是单分子层的吸附，但与Langmuir方程的区别是，没有假设吸附表面是均一的。表达式如下：

式中：

线性表达式为

式中：qe是平衡吸附量，mg/g；qm为最大吸附量，mg/g；k是吸附能力有关的常数，mg2/kJ2。

1.3 Freundlieh吸附等温模型

Freundlich等温方程是一个经验公式[7]，用于描述高浓度吸附质在不均匀表面条件下的吸附。表示如下：

式中：KF是Freundlich吸附系数，与吸附剂的性质和吸附条件有关；n是Freundlich常数，通常大于1，一般认为l/n=0.1～0.5时，易于吸附，而1/n＞2时则难以吸附。将式(6)两边取对数可得

以lgqe对lgeρ作图，直线的截距为lgKF，斜率为1/n。

Freundlich吸附方程与Langmuir方程不同的是，它适合于分析非均匀表面的吸附过程，在高浓度时不像后者那样趋于一定值，在低浓度时，也不会还原为直线关系。但缺点是无最大吸附量，不能用来估计参数浓度范围以外的吸附作用。

1.4 Temkin等温模型

Temkin吸附等温式的形式为[8]

或

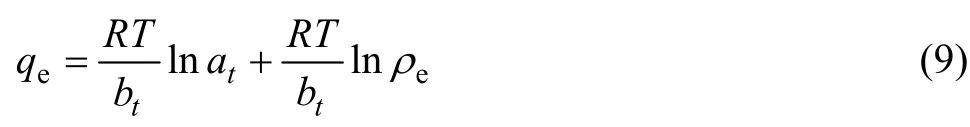
式(9)中at和bt分别为方程的两个常数，qe和eρ的意义同前。以qe对lgeρ作图为一直线，可确定该方程对实验数据的拟合程度。

根据吸附模型中有关能量的假设，上面这4种吸附方程反映了吸附过程中不同的能量关系。Langmuir方程所表示的能量关系是在吸附过程中吸附热不变，是一种理想的吸附；Freundlich方程所描述的能量关系是吸附热随吸附量的增加呈对数形式降低；而Temkin方程所描述的是吸附热随吸附量的增大呈线性降低。因此，Freundlich方程和Temkin方程适用于不均匀表面吸附行为。

1.5 Redlich-Peterson(R-P)等温模型

Redlich-Peterson吸附方程式[9]则是综合考虑了Freundlich等温吸附方程受低浓度的限制和Langmuir等温吸附方程受高浓度的限制的缺点而提出的较为合理的经验方程式，表示如下：

由式(10)可以看出，该方程式与Langmuir方程式很相似，只是多了一个Freundlich方程式中的指数，因此，该式同时具有Langmuir方程和Freundlich方程的特征。其中，A和B都是与吸附能力有关的常数；指数g为经验常数，介于0和1之间。

当g=1时，式(10)转化为Langmuir形式：

当g=0时，式(10)转化为Henry形式:

将式(10)取对数可转化成线性形式：

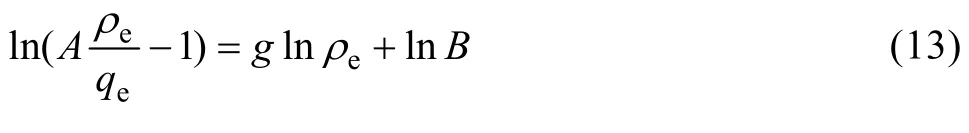
式中的参数A、B和g可以根据式(13)的线性关系式通过数值模拟方法计算。

1.6 Koble-Corrigan(K-C)等温模型

Koble-Corrigan(K-C)等温模型的一般形式为[10]

式(14)也是Langmuir和Freundlich模型的结合，其线性形式为

2 实验

2.1 试剂与仪器

硫酸铟(分析纯)，国药集团化学试剂有限公司生产；HCl、NaOH、H2SO4、HNO3、无水乙酸钠、乙醇和乙酸(分析纯)，北京化工厂生产；强酸性阳离子交换纤维[4]，本实验室自制。强酸性阳离子交换纤维直径为30～40 μm，全交换容量为3.5～4.2 mmol/g，使用前用1 mol/L的HCl浸泡24 h后，转成H+型，洗至中性，低温干燥。

752紫外可见分光光度计，上海奥普勒仪器有限公司生产；SHA-B型恒温震荡器，常州国华电器有限公司生产；AR2140型电子天平，Shimadzu公司生产；KQ-300E超声波清洗器，昆山市超声仪器有限公司生产。

2.2 In3+浓度的测定方法

采用5-Br-PADAP分光光度法测定In3+的浓度[11]。In3+浓度在质量浓度为0～500 μg/L时与吸光度呈良好的线性关系，标准曲线方程为：A=0.748ρ−0.010 6，R2=0.999 8。A为吸光度；ρ为In3+浓度，mg/L。

2.3 SACEF对水溶液中In3+的吸附等温线的测定

本研究采用瓶点法测定SACEF吸附In3+的等温吸附线。准确称取一系列不同质量的SACEF于具塞锥形瓶中，加入一定量相同浓度的In3+标准溶液，置于恒温振荡器中恒温振荡24 h，使吸附达到平衡，经紫外−可见分光光度计测定溶液中In3+的平衡浓度(eρ)。平衡吸附量qe(mg/L)根据下式计算：

式中：qe为平衡吸附量，mg/g；V是In2(SO4)3溶液的体积，L；m是干基离子交换纤维的质量，g；0ρ是In3+溶液的初始浓度，mg/L；eρ是In3+溶液的平衡浓度，mg/L。由此绘出离子交换纤维在293、303、313和323 K的吸附等温线。

3 结果与讨论

铟在水溶液中应该是以水合离子的形式存在。在络合物的生成过程，一般可以用以下的化学方程式进行描述[12]

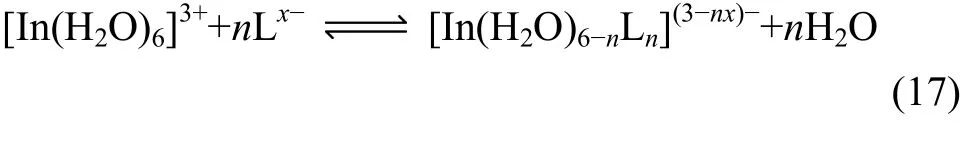
式中：L代表与溶液中的[In(H2O)63+]配位的任意络合阳离子。

铟的水溶液化学受制于水解作用开始时溶液的pH值。在pH值＜1.5时，溶液中铟的主要存在形式为In3+；在pH值为1.5～3.5时，溶液中铟的主要存在形式为In3+、InOH2+和In(OH)2+；pH＞3.5后，溶液中的开始出现In(OH)3。为保证溶液中的铟能以阳离子形式存在，故本文所研究溶液的pH值均控制在1.5～3.5之间，因此溶液中铟的存在形式主要为In3+、水合InOH2+和水合InOH2+。

3.1 等温吸附模型

本研究选用Langmuir、Dubini-Radushkevieh (D-R)、Freundlich、Temkin、Redlich- Peterson(R-P)和Koble-Corrigan(K-C)等6种等温吸附模型，分别在293、303、313和323 K等4个不同温度下用SACEF吸附In3+的等温实验数据进行线性和非线性拟合，比较这6种模型的特点和适用情况，拟合结果如图1～6和表1所示。

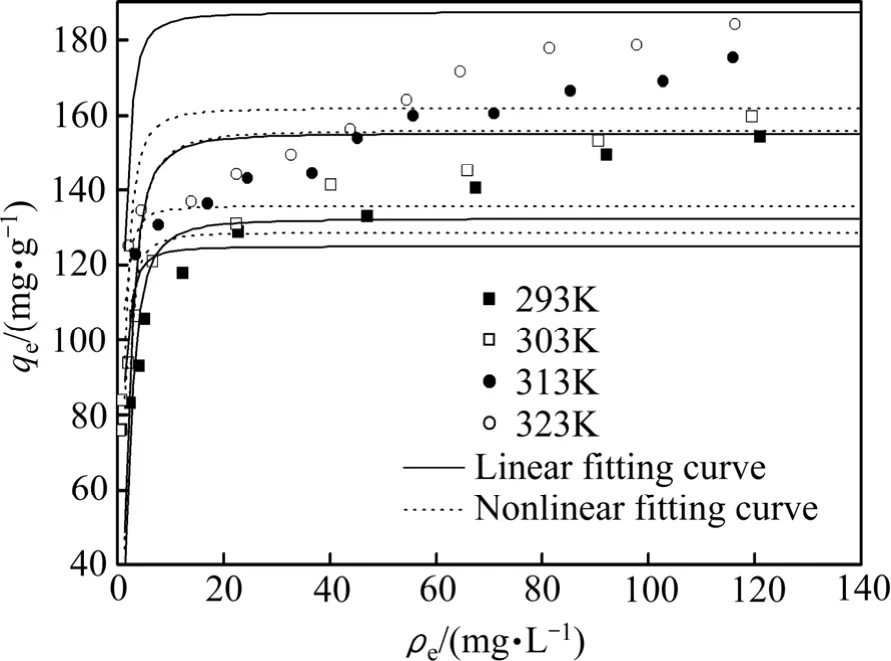
图2 SAAEF吸附In3+的Dubinin-Radushkevich(D-R)等温吸附模型拟合曲线Fig. 2 Fitting curves of isothermal adsorption Dubinin-Radushkevich model of SACEF adsorption In3+

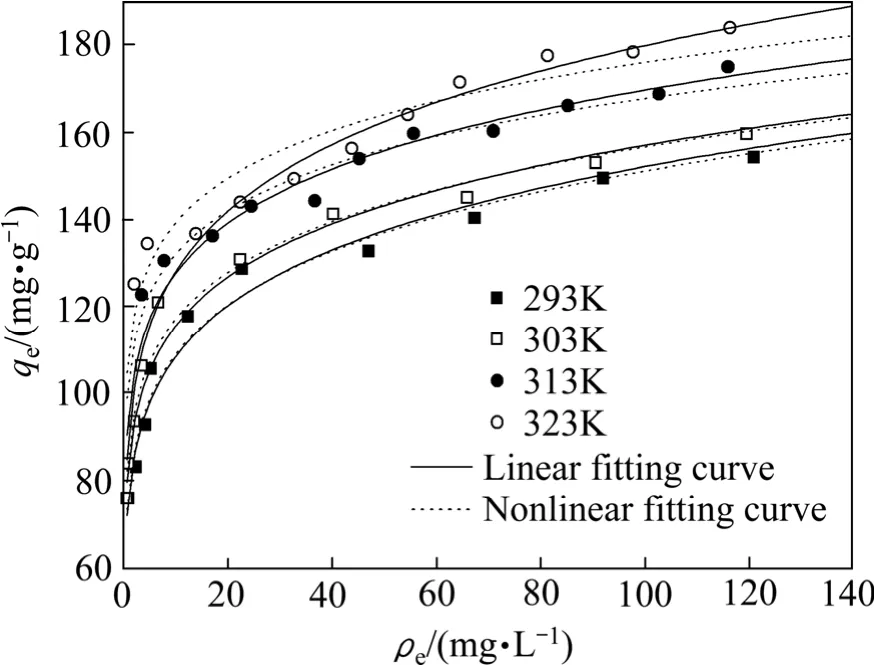
图3 SAAEF吸附In3+的Freundlich等温吸附模型拟合曲线Fig. 3 Fitting curves of isothermal adsorption Freundlich model of SACEF adsorption In3+

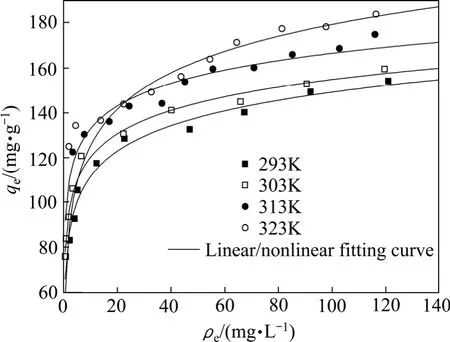
图4 SAAEF吸附In3+的Temkin等温吸附模型拟合曲线Fig. 4 Fitting curves of isothermal adsorption Temkin model of SACEF adsorption In3+

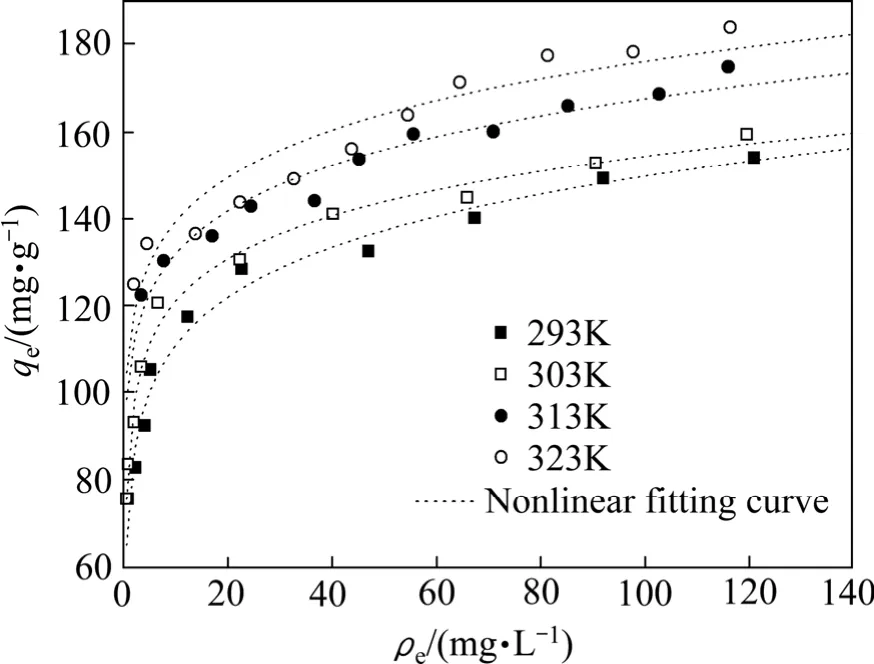
图5 SAAEF吸附In3+的Redlich-Peterson(R-P)等温吸附模型拟合曲线Fig. 5 Fitting curves of isothermal adsorption Redlich-Peterson model of SACEF adsorption In3+

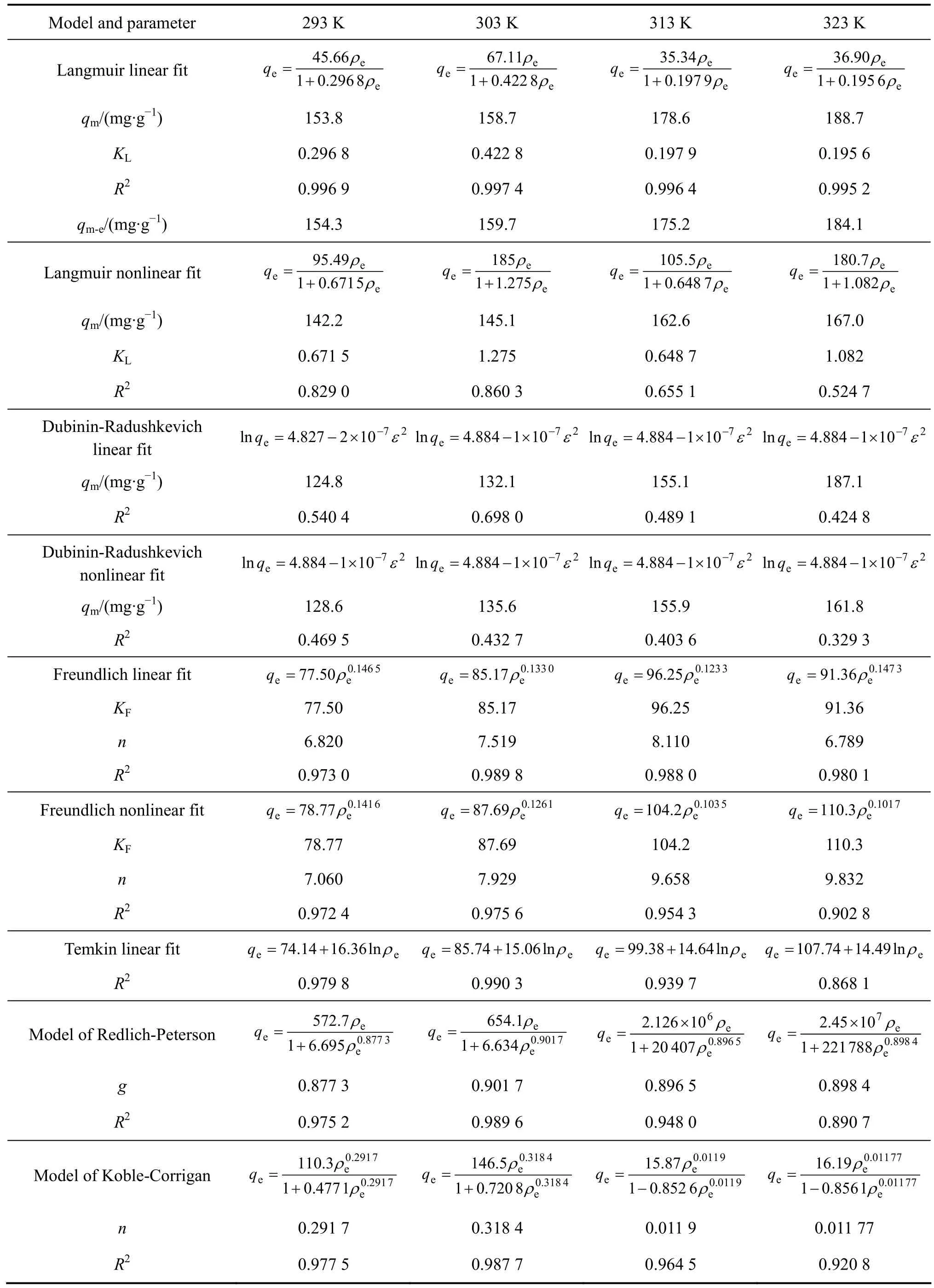
表1 SACEF吸附In3+的等温吸附模型Table 1 Isothermal adsorption of SACEF adsorption In3+

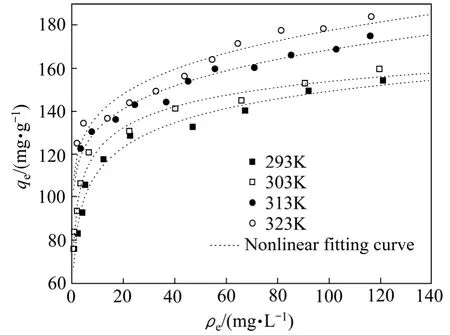
图6 SAAEF吸附In3+的Koble-Corrigan等温吸附模型拟合曲线Fig. 6 Fitting curves of isothermal adsorption Koble-Corrigan models of SACEF adsorption In3+

对于固液体系的吸附行为，常用Langmuir吸附等温式来描述。Langmuir模型假设吸附是单分子层的，常数qm表示单分子层吸附饱和时的吸附量；KL表示SACEF对水合In3+离子的结合力的大小。由图1和表1看出，线性分析的回归系数大于非线性回归分析方法，但由于处理方法不同，两种回归系数没有可比性。随着温度的升高，KL值和qm值均增大，这说明温度的升高有利于SACEF对水合In3+离子的吸附，该吸附过程是吸热的，这与吸附热力学计算的结果是相符合的。

Dubinin-Radushkevich模型描述的也是单分子层的吸附，但与Langmuir模型不同的是它没有假设吸附表面是均一的。从表1和图2中可以看出，虽然最大吸附量qm随着温度的升高而增大，但与实际的实验值qm-e相差较大，相关系数也不高，拟合程度也不好，所以不适合用来描述SACEF对水合In3+离子的吸附行为。

Freundlich方程可用于对非均匀表面的吸附剂和高浓度溶质的吸附过程进行描述。从图3和表1可以看出，线性拟合和非线性拟合分析得到的1/n值都小于0.2，说明在实验的温度下SACEF对水合In3+离子的吸附是优惠吸附，吸附较容易进行[13]。Freundlich吸附系数KF值在线性拟合和非线性拟合中均随温度的升高而增大，说明随着温度的升高，SACEF与水合In3+离子间的作用力增强，吸附强度随着活化温度的升高而升高，温度的升高有利于SACEF对水合In3+离子的吸附。从图1和图3中也可以看出，Freundlich方程和Langmuir线性拟合方程对实验数据的拟合程度都比较好，区别只是在高浓度时，Freundlich方程不像Langmuir方程那样趋于一定值，在低浓度时，也不会还原为直线关系。

Temkin方程和Freundlich方程一样，也适用于描述不均匀表面吸附。它的线性拟合形式和非线性拟合形式相同，故两种形式的参数也都相同。参数A和B值均随温度的升高而增大，相关系数R2值也均在0.90左右，说明可以用Temkin方程来描述SACEF对水合In3+离子的吸附行为。

Redlich-Peterson模型和Koble-Corrigan模型都是Langmuir模型和Freundlich模型的结合。从表1可以看出，参数A值和B值变化均无规律，g值均介于0和1之间，且接近于1，可见Redlich-Peterson方程趋近于Langmuir方程，其相关系数R2值较大，表明SACEF对水合In3+离子的吸附等温线与Redlich-Peterson等温模型符合即较好，说明吸附剂存在的非均匀空隙或SACEF主要为表面吸附位，对水合In3+离子的吸附并不是均匀的单层吸附。而Koble-Corrigan模型拟合结果中，指数n值介于0和1之间，且与1相差较大，所以Koble-Corrigan方程与Langmuir方程相差较远。从拟合的相关系数来看，在293～313 K时，Redlich-Peterson模型和Koble-Corrigan模型的R2值都在0.95以上，说明在这个温度范围内可以用这两种模型来描述SACEF对水合In3+离子的吸附行为。

从这6种模型综合来看，除了Langmuir非线性拟合和Dubinin-Radushkevich模型以外，其它模型的拟合程度都较好，相关系数R2值都在0.9左右。综合考虑相关系数来看，Langmuir模型(线性拟合)最适合用来描述SACEF对水合In3+离子的吸附行为。

3.2 吸附热力学公式

3.2.1 吸附焓ΔH的计算

由Van’t Hoff方程[14]：

式中：ρ为吸附平衡时的平衡浓度，mg/L；T为绝对温度，K；R为摩尔气体常数；ΔH为等量吸附焓，kJ/mol；K为常数。通过测定各种温度下SACEF对水合In3+离子的吸附等温线，再由吸附等温线绘出不同等吸附量时的吸附等量线lneρ—1/T，如图7所示。用线性回归法求出各吸附等量线所对应的斜率，计算出不同吸附量时In3+的等量吸附焓。

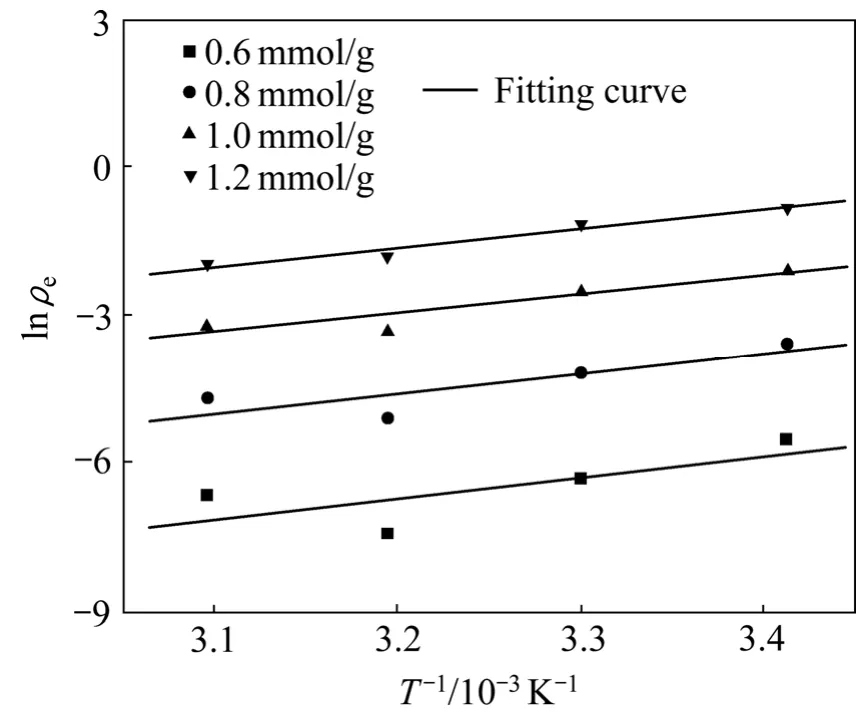
图7 SACEF吸附In3+的等量吸附线Fig.7 Estimated of thermodynamic parameters of system tested (for In3+on SACEF)

3.2.2 吸附自由能ΔG的计算

吸附自由能ΔG的值可以通过Gibbs方程从吸附等温线衍生得到[15]

式中：q为吸附量，mol/g；x为溶液中吸附质的摩尔分数。

如果q和x的关系符合Freundich方程，即

将式(20)代入式(19)得到的吸附自由能与q无关。

式中：n为Freundlich方程指数

3.2.3 吸附熵ΔS的计算

吸附熵可按Gibbs-Helmholtz方程计算[16]：

由于图1所示吸附等温线符合Freundlich等温方程，所以本研究按式(7)计算吸附焓ΔH，按式(21)求算吸附自由能ΔG，吸附熵ΔS按式(22)计算。表2为不同吸附量下的等量吸附焓ΔH、吸附自由能ΔG以及吸附熵ΔS的热力学参数的数据计算结果。

从表2的数据可以看出，ΔH大于0，表明此SACEF对水合In3+离子(包括In3+、水合InOH2+和水合InOH2+离子3种状态)的吸附过程是吸热的，且ΔH的绝对值随着吸附量的增加逐渐降低，其原因可能是SACEF中含亲水性很强的磺酸基(—SO3H)基团，使SACEF吸附有许多水分子。当该离子交换纤维要吸附水合In3+离子时，实际上就是要先解吸水分子，然后才能再吸附水合In3+离子。由于水合In3+离子的分子量比水分子大很多，而其体积相应也比水分子大很多，因此吸附一个水合In3+离子到纤维上就需要占据较大的空间，必须解吸较多的水分子。解吸过程是一个吸热的过程，而通常吸附过程是一个放热过程[17−18]。由于吸附一个水合In3+离子需要解吸多个水分子，这就导致解吸过程吸收的热量大于吸附过程放出的热量，最终导致吸附水合In3+离子的全过程为吸热过程。

吸附焓ΔH随吸附量的增加而略有降低，这可能是由于SACEF表面的不均匀性引起的。因为在较低浓度时，吸附质与吸附剂之间的作用主要是吸附质与吸附剂之间的直接作用，纤维表面的不均匀性使水合In3+离子优先占据能量有利的位置，并且水合In3+离子的分子量和体积比水分子的大很多，所以随着吸附量的增加，纤维的表面被覆盖的程度也增大，吸附质与吸附剂之间的作用逐渐被吸附在纤维上的水合In3+离子与溶液中的水合In3+离子的作用所取代，吸附焓ΔH逐渐下降。

吸附自由能ΔG是吸附驱动力和吸附优惠性的体现。从表2的数据可以看出，吸附自由能都为负值，说明SACEF对水合In3+离子的吸附过程是自发进行的，即水合In3+离子容易被SACEF吸附。而吸附熵ΔS总是正值，这是因为水的分子量和分子体积比水合In3+离子的小很多，离子交换纤维在吸附水合In3+离子后，使水合In3+离子的运动比在水溶液中的运动更规则，即水合In3+离子在纤维上的运动不如在水溶液中的运动自由。因此，对于离子交换纤维吸附水合In3+离子来说应是一个熵变减少的过程。但在离子交换纤维吸附水合In3+离子的同时有大量水分子被解吸下来，对水分子来说，其解吸过程就是由原来在纤维上的整齐、紧密排列的水分子解吸后变成在水溶液中自由运动的水分子，因此，这是个熵增的变化，其熵变很大，最终导致该离子交换纤维吸附水合In3+离子全过程的总熵变为正值。

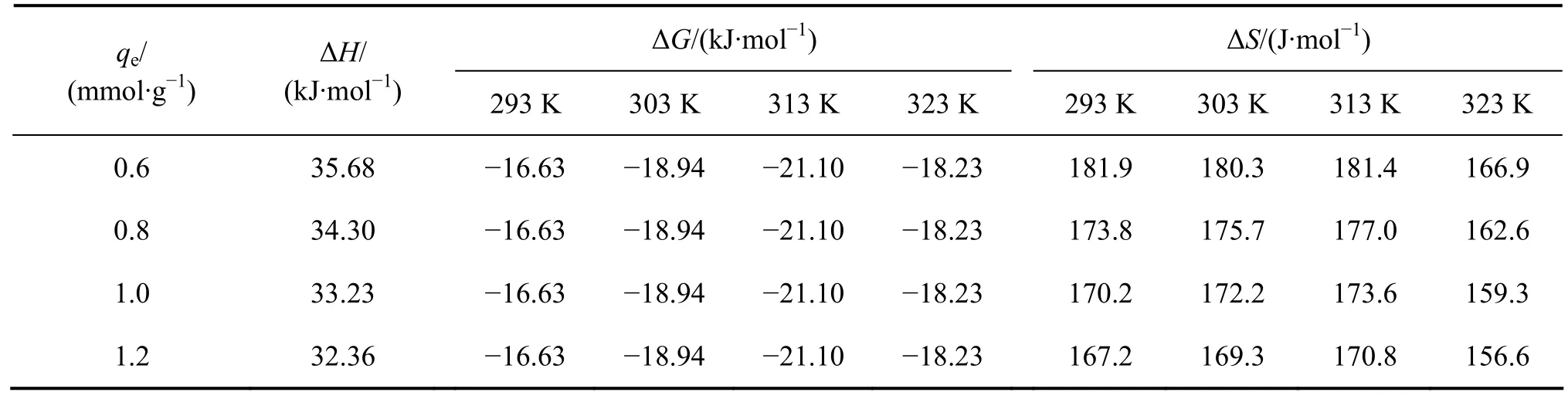
表2 SACEF吸附In3+的热力学参数Table 2 Thermodynamics parameters for adsorption In3+onto SACEF from water

4 结论

1) 采用瓶点法测定了SACEF对水合In3+离子的等温吸附平衡曲线。平衡数据采用Langmuir、Dubini-Radushkevieh(D-R)、Freundlich、Temkin、Redlich-Peterson(R-P)和Koble-Corrigan(K-C)等6种等温吸附模型进行线性和非线性拟合。

2) 除Langmuir非线性拟合及Dubini-Radushkevieh模型之外，其余模型的线性及非线性拟合结果均较好，可以用于描述强酸性阳离子交换纤维吸附水中In3+的等温吸附行为，其中Langmuir模型(线性拟合)最为适合。

3) 通过对SACEF吸附水合In3+离子的等量吸附热力学函数的计算得知，水合In3+离子在SACEF上的吸附焓总是大于零的，强酸性离子交换纤维对水合In3+离子的等量吸附焓随着吸附量增大而增大，表明吸附过程是一个吸热过程。

4) SACEF对水合In3+离子的吸附自由能为负值，表明SACEF对水合In3+离子的吸附具有较强的驱动力，水合In3+离子较容易被SACF吸附，SACEF吸附水合In3+离子的总吸附过程是熵增的。

REFERENCES

[1]冉俊铭, 伍永田, 易健宏. 铟产业发展现状及展望[J]. 世界有色金属, 2008(1): 26−28. RAN Jun-ming, WU Yong-tian, YI Jian-hong. Present situation and development of indium industry[J]. World Nonferrous Metals, 2008(1): 26−28.

[2]周智华, 莫红兵, 徐国荣, 唐安平. 稀散金属铟富集与回收技术的研究进展[J]. 有色金属, 2005, 57(1): 71−76, 80. ZHOU Zhi-hua, MO Hong-bing, XU Guo-rong, TANG An-ping. Progress in indium recovery and pre-concentration technology[J]. Nonferrous Metals, 2005, 57(1): 71−76, 80.

[3]邹家炎. 铟的提取、应用和新产品开发[J]. 广东有色金属学报, 2002, 12(9): 16−20. ZOU Jia-yan. Extraction and application of indium and development of its new products[J]. Journal of Guangdong Non-ferrous Metals. 2002, 12(9): 16−20.

[4]李 凯, 曾庆轩, 李明愉. 强酸性离子交换纤维的制备及其吸附性能研究[J]. 精细石油化工进展, 2005, 5(10): 38−41. LI Kai, ZENG Qing-xuan, LI Ming-yu. Preparation of strong acidic cation exchange fibers and study on sulfonation and adsorption properties[J]. Advances in Fine Pethochenicals, 2005, 5(10): 38−41.

[5]LANGMUIR I. The constitution and fundamenial properties of solids and liquids[J]. Journal of America Chemistry Soeiety, 1916, 38: 2221−2295.

[6]UNLU N, ERSOZ M. Adsorption characteristies of heavy metal ions onto a low cost biopolymeric sorbent from aqueous solutions[J]. Journal of Hazardous Materials, 2006, 136(2): 272−280.

[7]FREUNDLICH H M F. Uber die adsorption in lasungen[J]. Physical Chemistry, 1906, 57: 385−470.

[8]GUIBAL E, SANEEDO I, ROUSSY J. Uptake of urallylions by new sorbing Polymers: discussion of adsorption isotherm and pH effet[J]. Reactive Polymers, 1994, 23(2/3): 147−156.

[9]REDLICH O, PETERSON D L. A useful adsorption isotherm[J]. Physical Chemistry, 1959, 63: 1024.

[10]LANGUMIR I. The constitution and fundamental properties of solids and liquids[J]. Journal of America Chemistry Society, 1916, 38: 2221−2295

[11]朱晓华, 叶菊林. 巯基棉富集分离—5-Br-PADAP分光光度法测定铟[J]. 冶金分析, 1984(4): 15−17. ZHU Xiao-hua, YE Ju-lin. Determination indium by spectrophotometry with 5-Br-PADAP with separating and enriching of sulfhydryl cotton[J]. Metallurgical Analysis, 1984(4): 15−17.

[12]张启运, 徐克敏. 铟化学手册[M]. 北京: 北京大学出版社, 2005: 159. ZHANG Qi-yun, XU Ke-min. Indium chemical manual[M]. Beijing: Beijing University Press, 2005: 159.

[13]何炳林, 黄文强. 离子交换与吸附树脂[M]. 上海: 上海科学技术出版社, 1995. HE Bing-lin, HUANG Wen-qiang. Ion exchange and adsorption resin[M]. Shanghai: Shanghai Science and Technology Press, 1995.

[14]北川浩, 铃木谦一郎. 吸附的基础与设计[M]. 鹿政理, 译.北京: 化学工业出版社, 1983. KITAGAWA H, SUZUKI I. The fundamentals and designs for adsorption[M]. LU Zheng-li, transl. Beijing: Chemical Industry Press, 1983.

[15]GARCLA-DELGADO R A, COTOUELO-MINGUEZ L M, RODFIGUEZ J J. Equilibrium study of single-solute adsorption of anionic surfactants with polymeric XAD resins[J]. Sep Sci Technol, 1992, 27(7): 975−987.

[16]LONG Chao, LU Zhao-yang, LI Ai-min, LIU Wei, JIANG Zhen-mao, CHEN Jin-long, ZHANG Quan-xing. Adsorption of reactive dyes onto polymeric adsorbents: effect of pore structure and surface chemistry group of adsorbent on adsorptive properties[J]. Separation and Purification Technology, 2005, (44): 91−96

[17]姜志新, 谌竟清, 宋正孝. 离子交换分离工程[M]. 天津: 天津大学出版社, 1992. JIANG Zhi-xin, CHEN Jing-qing, SONG Zheng-xiao. Ion exchange separation engineering[M]. Tianjing: Tianjing University Press, 1992.

[18]傅献彩, 沈文霞, 姚天扬. 物理化学[M]. 北京: 高等教育出版社, 1990. FU Xian-cai, SHEN Wen-xia, YAO Tian-yang. Physical chemistry[M]. Beijing: Higher Education Press, 1990.

(编辑 李艳红)

Thermodynamic of adsorption of indium on strong acidic cationic exchange fiber

LI Ming-yu, ZENG Qing-xuan, LI Jian-bo, FENG Chang-gen
(State Key Laboratory of Explosion and Technology, Beijing Institute of Technology, Beijing 100081, China)

Adsorption of In3+from aqueous solution by strong acid cationic exchange fiber (SACEF) was studied using batch experiments. Langmuir, Dubinin-Radushkevich (D-R), Freundlich, Temkin, Redlich-Peterson(R-P)and Koble-Corrigan (K-C) models were applied to analyze the adsorption equilibrium data of In3+on SACEF obtained with researching range of concentration at 293−323 K through linear fitting and nonlinear fitting methods. The results show that, except for Langmuir nonlinear fitting and Dubini-Radushkevieh models, the adsorption equilibrium data can be well interpreted by both the linear fitting and nonlinear fitting of the models with theR2values about 0.9. Out of all the models, Langmuir linear fitting model is the suitable model with highest linear fittingR2value. The value of isosteric enthalpy indicates that the endothermic nature of the adsorption of In3+on SACEF. The adsorption of In3+on SACEF is an endothermic, spontaneous and entropy increase process with ∆H＞0 and reasonable explanation is given to the adsorption behavior.

strong acidic cationic-exchange fiber (SACEF); In3+; isothermal adsorption model; adsorption thermodynamic

TQ425.21+2

A

北京理工大学校基础基金资助项目(20080242009)

2011-09-21；

2012-03-30

李明愉，讲师，博士；电话：010-68915065；E-mail: mingyuli@163.com

1004-0609(2012)10-2846-09