采用响应曲面分析的声屏障优化设计
张林,殷承启,仝凯,胡婕
(江苏省交通规划设计院股份有限公司,南京210000)
近年来,声屏障作为最实用、有效的交通噪声防治措施之一,在交通环保领域得到广泛的应用[1,2]。在同一段声屏障保护范围内,由于各处房屋高度、路肩高差、至路肩距离等众多因素不尽相同,声屏障会对各保护目标产生不同的降噪效果;而对于同一处受声点,声屏障设计高度、长度和起始位置也会对插入损失及工程造价带来显著差异[3]。对江苏省高速公路沿线声屏障应用现状的调查研究表明,部分声屏障设计长度、高度不足,或者安置位置不合理,保护区域内声环境质量不能完全达标。通过合理的数理模型对声屏障设计参数进行优化,是声屏障设计工作中一个值得探讨的问题。
国内对声屏障工程的优化设计研究已取得若干积极成果。结合工程实践,利用Cadna/A[4]、SYSNOISE[5]等声学分析软件模拟声波辐射、散射和传播过程,可以实现对声屏障降噪效果和等声级线分布预测。然而这些研究大多以声屏障设置路段内特定位置的声学响应为单一优化指标,对保护范围内多处敏感目标的降噪优化研究,以及声屏障工程造价的控制却少有关注;因而,难以实现声屏障工程的最佳综合环境效益。
响应曲面法(response surface methodolo-gy)是20世纪发展起来的一种综合实验设计与数学建模的新型优化方法,在多因素优化分析研究中表现出显著的优越性。通过在给定区域上构建因素与响应值间的明确函数关系,可以寻求满足多个响应值的各因素最佳组合[6,7]。笔者以常嘉高速公路碛砂村路段声屏障设计为算例,基于声屏障插入损失预测模型和minitab分析软件,应用RSM法对声屏障设计长度、高度和起始桩号位置等3个因素进行全面考察和优化,以期为声屏障优化设计及提高其适用性提供理论依据。
1 声敏感区域现状与噪声预测
常嘉高速公路路线穿越碛砂村,施工期道路用地红线内房屋将被拆迁;营运期间,沿线用地红线外房屋会受到一定程度的交通噪声影响,主要居民点与路线位置关系如图1所示。从图可见,碛砂村多排房屋与路线平行分布,主要以二层楼房为主,选取K3+880、K3+795和K3+760处首排房屋为代表受声点,可以较好的反映该处村落受交通噪声的影响程度,如表1所示。
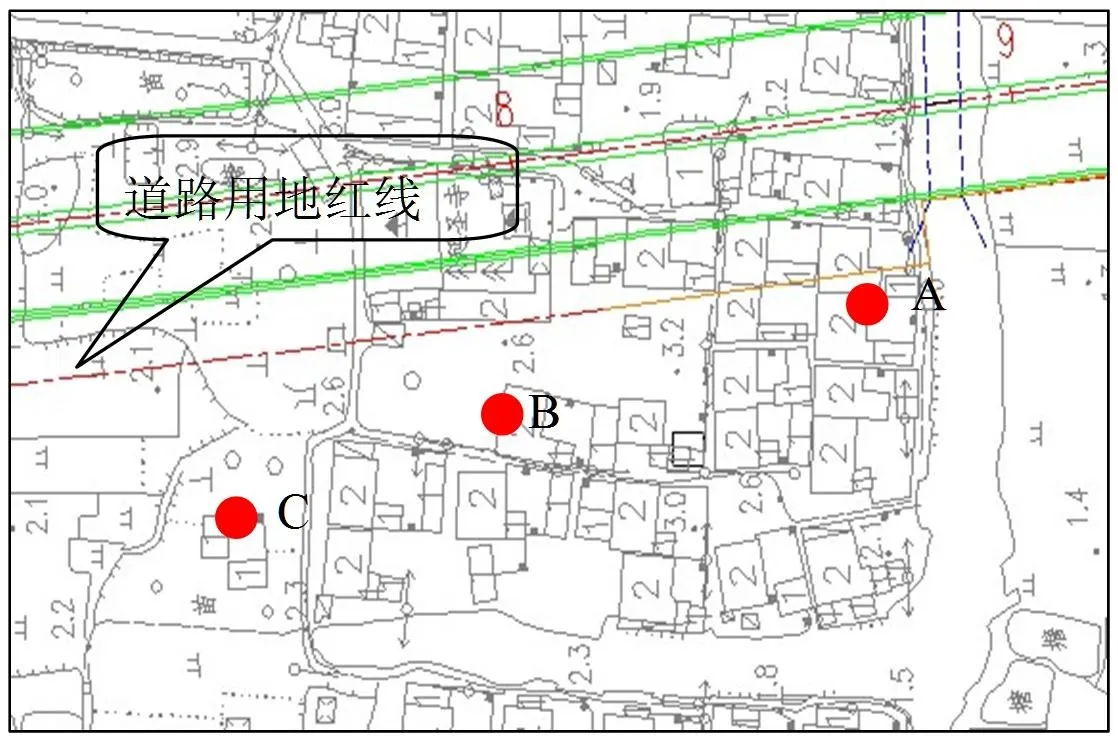
图1 碛砂村主要居民分布点Fig.1 Settlements distribution of Zisha village

表1 碛砂村交通噪声影响预测Tab.1 Prediction of influence of traffic noise on Zisha village
2 数理模型建立
2.1 模型假设
为避免构建数学模型过于繁冗难以分析,在建模过程中做出以下合理假设:
(1)交通噪声源为无限长线声源,取500 Hz为声源等效频率;
(2)声屏障型式为直立型,不考虑屏体吸声作用、透射声、反射声对声屏障插入损失的影响;
(3)受声点至道路隔离栅之间为平坦疏松地面。
2.2 设计因素与水平
根据惠更斯―菲涅尔原理计算无限长声屏障绕射声衰减量,并进行遮蔽角百分率、地面吸声衰减等物理量修正。得到有限长声屏障理论插入损失[9]。
基于理论插入损失计算方法和以上假设,选取影响声屏障对各受声点插入损失的三个重要变量:声屏障设计高度、长度、起点桩号,分别以X1、X2、X3代表。每个自变量的低、中、高设计水平分别以-1、0、+1编码。
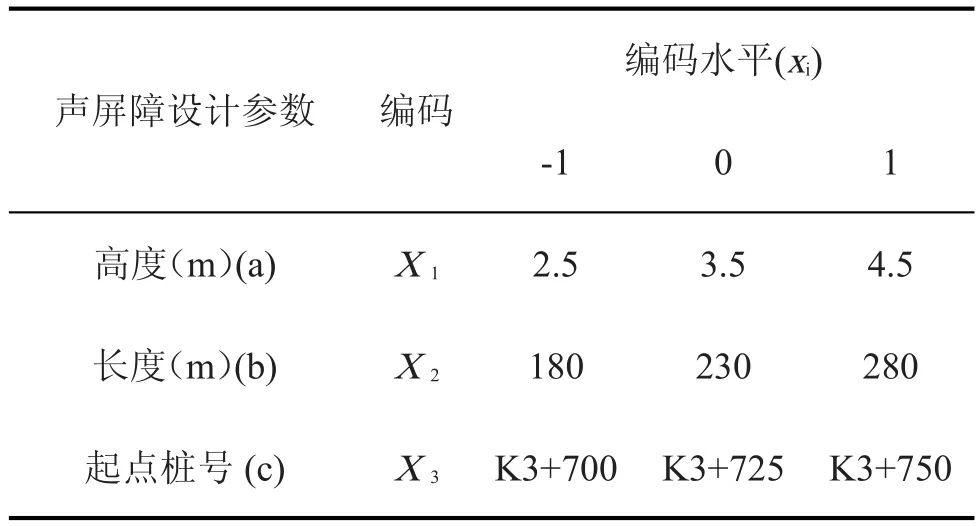
表2 响应曲面设计因素与水平Tab.2 Factors and levels in response surface design
2.3 设计方案与结果
根据Box-Behnken的中心组合设计原理与方法,利用minitab软件自动生成声屏障设计方案,计算不同方案下声屏障对各受声点的插入损失。声屏障工程造价仅考虑上部屏体材料、下部地梁、桩基础等成本费用。参照江苏省部分高速公路声屏障工程概算,得到声屏障造价经验公式为
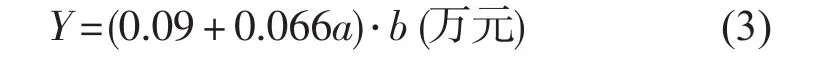
式中a、b分别为声屏障设计高度,设计长度。
2.4 构建多元二次回归模型
利用minitab设计软件对表3中数据整理分析拟合,可得二次多元回归模型,描述因变量与自变量变化关系模型如下
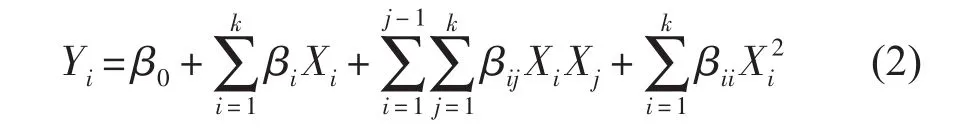
式中Yi为因变量响应值,β0、βi、βii、βij分别为常数项、线性系数、交互项系数和二次项系数,Xi为自变量。
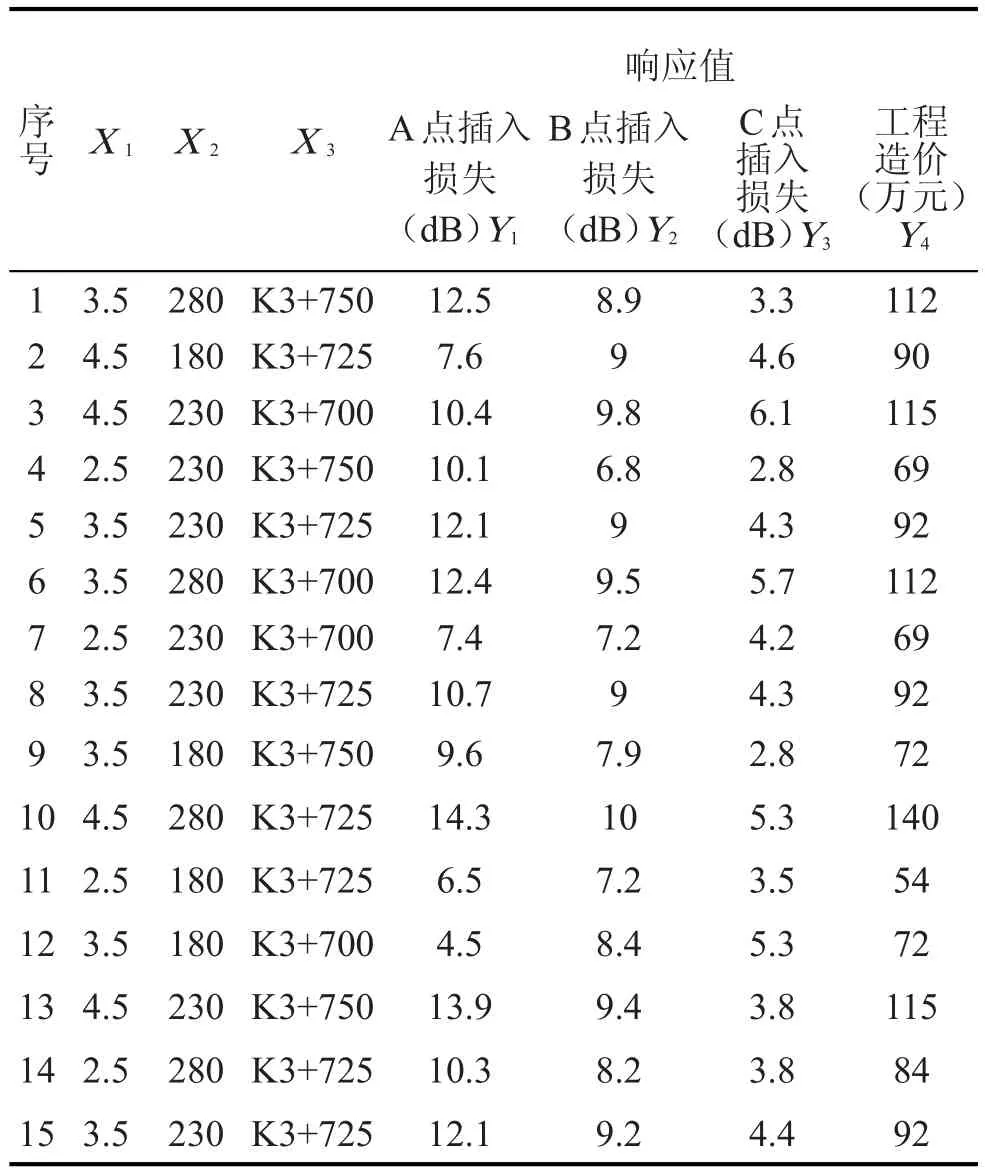
表3 响应曲面设计方案与结果Tab.3 Programand results of response surface methodlogy
以声屏障设计高度、长度和起点桩号为自变量,A、B、C三处受声点插入损失为响应值的二次多元回归方程分别为

2.5 回归模型显著性检验
对各回归方程系数及方程模型进行F检验和P检验,方差分析和显著性检验结果如表4所示。
软件分析结果显示:对各受声点声屏障插入损失建立的二次回归模型相关系数R2≥0.973 6,校正相关系数R2adj≥0.926 1,P值≤0.000 9;拟合不足部分P值≥0.106 1。这说明各回归模型拟合度较高,可以较好地反映声屏障设计参数对各受声点插入损失的影响规律。
3 响应曲面分析
声屏障各设计参数对插入损失的影响程度,决定于受声点与线声源的空间位置关系。根据模型生成的响应曲面及相应等高线图,对各设计参数进行显著性影响分析,如图4所示。曲面斜率可以反映各因素的影响显著性水平,等高线弯曲程度可反映因素间交互作用的强弱[10]。
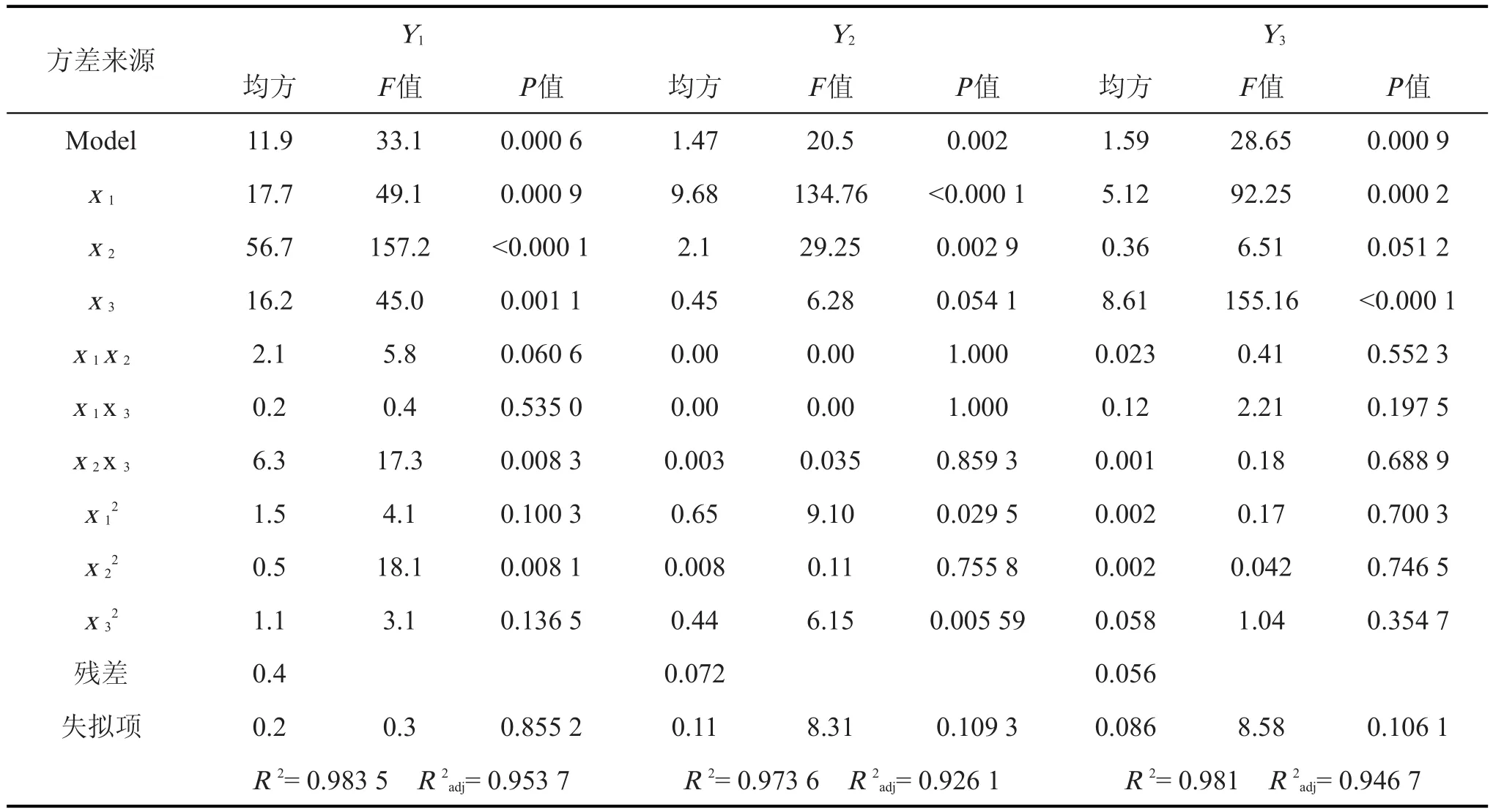
表4 回归模型方差分析与显著性检验Tab.4 Variance analysis and significance test of regression models

图4 声屏障设计水平影响插入损失响应面与等高线图Fig.4 Response surface and contour plots of noise barrier parameter on insertion loss
A点插入损失受声屏障设计高度、长度和起点桩号等因素影响均较为显著。这是由于A点距路肩很近,声屏障高度的变化对绕射声程差影响较大;同时A点位于碛砂村东侧,靠近声屏障设置终点,声屏障长度和起始桩号位置是决定遮蔽角百分率的主要因素。B点位于声屏障保护范围的中部位置,遮蔽角百分率受声屏障设置路段范围的制约程度较小,故声屏障起始桩号位置对B点插入损失影响不显著。C点距路肩较远,交通线声源有效长度较A点、B点增加,延长声屏障对增大遮蔽角百分率意义不大,故C点插入损失受声屏障设计长度影响不显著。这与方差分析中一次项系数P值检验结果是一致的。
4 模型优化求解
声屏障工程设计实例中,其高度、长度和设置路段范围不仅取决于声敏感点的目标降噪值,同时受到工程造价和公路沿线设备设施的制约。为实现设计声屏障实用性和经济性的统一,利用minitab软件中重叠等值线功能对声屏障设计参数进行优化。声屏障技术经济指标设定为:各处受声点夜间噪声达标;工程造价控制在73万元以下。
由图5可得到满足设定目标条件的优化区域。使用minitab优化器绘制优化图,从优化区域内分析得到最佳设计参数:声屏障设计高度3.7 m,设计长度214 m,起点、终点桩号分别为K3+728和K3+942。在此设计条件下,预测声屏障工程对A、B、C处居民房屋的插入损失分别为:11.1 dB、9.1 dB和4.4 dB,可以满足各受声点声环境质量标准;声屏障工程造价约为71.7万元。
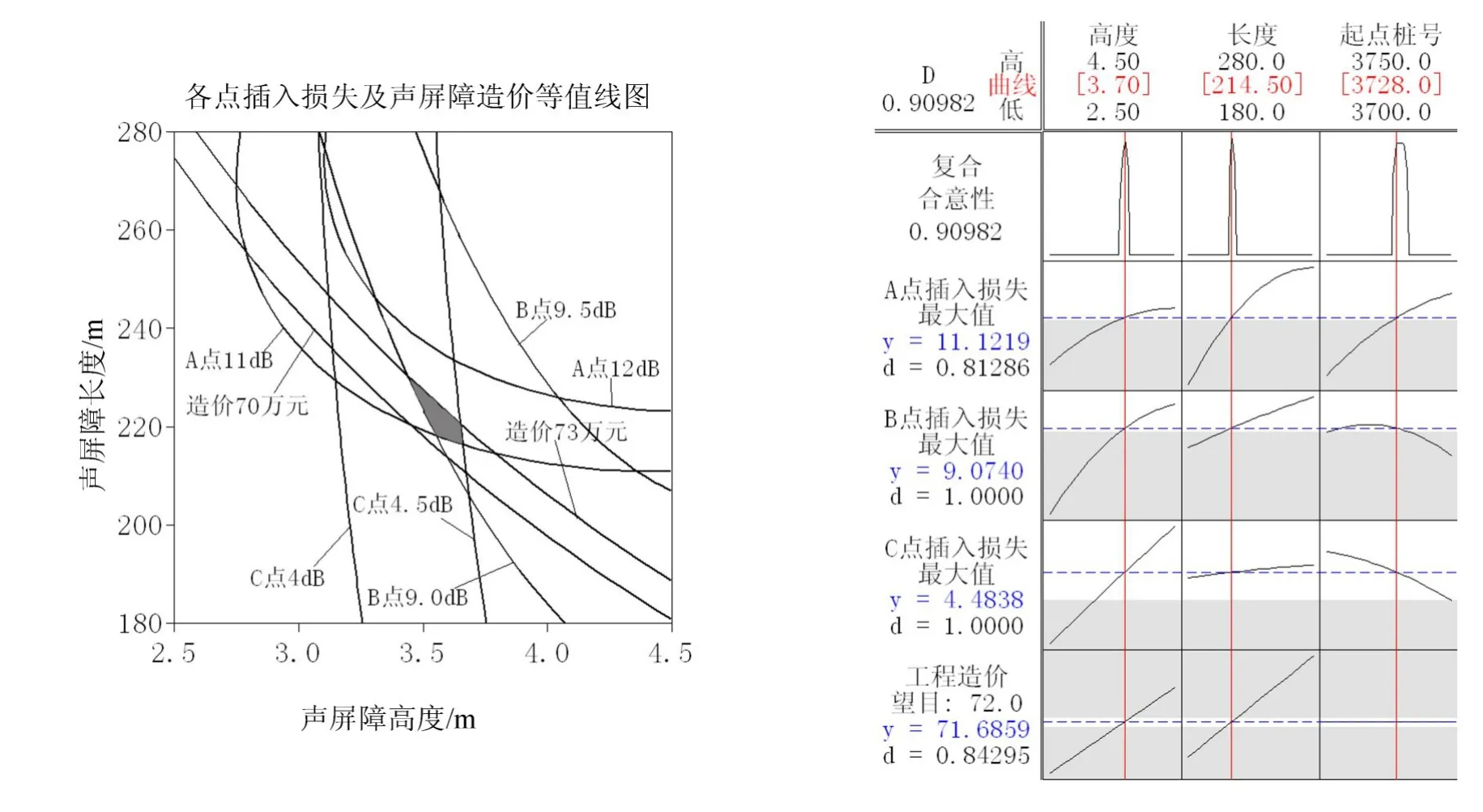
图5 重叠等值线和响应优化器求解图Fig.5 Optimal solution obtained by overlay contour plots and RSmoptimizer
5 结语
根据响应曲面设计方法对声屏障设计参数进行优化分析研究,并结合对江苏省部分高速公路声屏障工程的现场调查和声学性能评价,为交通领域声屏障设计工作提供以下参考借鉴:
(1)声屏障对保护区域内敏感目标的降噪效果,是声屏障设计参数和敏感目标空间位置共同作用的结果。根据保护区域内自然地理特征,选取代表性受声点作为声屏障设计计算点,是确保声屏障声学性能的重要前提;
(2)传统声屏障设计方法,难以实现对各敏感目标噪声超标量统筹兼顾。利用minitab软件中响应曲面优化分析,可综合考虑设计参数对各敏感目标插入损失的影响规律和工程造价的约束,实现声屏障工程最佳综合环境效益;
(3)声屏障实际降噪效果需考虑地面障碍物衰减、屏体吸声作用的影响。完善声屏障设计模型,在优化分析软件嵌入声学计算模块,将会是下一步研究的重要方向。
[1]卢向明.道路声屏障声学特性与声学设计研究[D].杭州:浙江大学环境与资源学院,2004.
[2]魏显威,尚晓东.高速公路声屏障设计中几个问题的探讨[J].公路交通科技,2002,(12):184-186.
[3]公路声屏障设计与施工若干关键技术问题探讨[J].公路,2011,(2):176-179.
[4]沙学锋,李新春,郭栋.基于SYSNOISE的环境敏感点声屏障设计仿真研究[J].长春理工大学学报(自然科学版),2010,(2):75-78.
[5]张磊,刘丹,王国良.浅谈申嘉湖杭高速公路(湖州段)声屏障设计[J].公路,2010,(9):215-220.
[6]赵健植,金保升,仲兆平.基于响应曲面法的除雾器叶片效率模拟[J].中国电机工程学报,2007,(8):61-64.
[7]Hasan D M,Melo N C,Rubens M,et al.Simulation and response surface analysis for the optimization of a three-phase catalytic slurry reactor[J].Chemical Engi neering and Processing,2005,44(3):335-343.
[8]HJ 2.4-2009.环境影响评价技术导则―声环境[S]
[9]HJ/T90-2004,声屏障声学设计和测量规范[S].
[10]Catalkaya E.C.,Kargi F.Advanced oxidation and min-eralization of simazine using Fenton’s reagent[G].Journal of Hazardous Materia ls,2009,168(2-3):688-694

