变速比齿条齿廓设计计算新方法*

贺敬良 王成武 田燕林

(①北京信息科技大学，北京 100192;②中国石油昆仑燃气有限公司，北京 100101)

要进行变速比齿条的强度有限元分析、虚拟装配和运动仿真以及最终的加工，一定要知道它的齿面形状。目前所用的方法，一般是由啮合理论出发，推导其共扼曲面的解析表达式［1－2］。对于定速比齿轮传动这种设计方法已经很成熟。

对于变速比转向器，为了获得良好的性能，要求齿条的传动比是变化的。对于变传动比齿条齿廓的求解，如果使用啮合方程推导齿条齿面的表达式不仅困难，而且还有不少缺点，如左右齿面啮合需要作为两种情况分别考虑，增加了计算工作量。当重合度大于1时，啮合方程的解不唯一，也就是说在一个瞬时接触线上可能有几个齿接触，给这时齿面求解计算方法的设计带来一定困难［3－4］。因此，基于啮合原理的传统分析方法很难满足变速比齿条的精确几何建模及最终数控加工的要求。

如果采用离散化的共轭曲面直接计算方法，即数值计算方法［5－6］，而不使用啮合方程，只需要已知齿轮参数与具体的运动要求，即可求解变速比齿条单个截面齿廓，且精度可以调节。但是在求解过程中仍然需要大量的编程，得到的齿廓曲线是由离散的点组成的，这样在曲线拟合过程中可能存在着一些问题，需要根据啮合原理的知识和实践经验进行判断，曲线拟合得是否正确。此外得到的是各个截面齿廓的数值，对于后续的仿真和数控加工仍然需要根据求解得到的齿廓数据建立齿轮的三维模型。

针对以上变速比齿条齿廓求解问题，提出了一种齿廓设计计算的新方法。只需要知道传动比规律和齿轮的参数，就可快速得到变速比齿条的三维精确数据模型;为变速比齿条齿廓的加工和测量提供了可靠的齿面数据;不需要大量的编程，简单明了、实用性强。

1 变速比齿条齿廓设计计算新方法

已知齿轮参数和运动要求，求齿条的共扼曲面。设齿条坐标系为xyz，齿轮坐标系为xhz，它们的原点重合，坐标轴y与坐标轴h的夹角为交错角ζ，如图1所示。

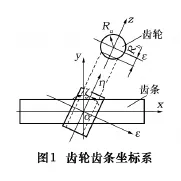
变速比齿轮齿条传动中，齿轮是一个参数特殊的渐开线圆柱斜齿轮，因而齿轮的齿廓是渐开线螺旋面，而齿条齿廓是在变传比条件下渐开螺旋面的共轭曲面，与斜齿非圆齿轮齿廓的形成是截然不同的，斜齿轮非圆齿轮传动两个齿轮的齿廓可以看作是在同一把法向齿廓为直线的媒介直齿条展成的，属间接包络成形;而这里的两个齿廓是先给出齿轮的齿廓，齿条的齿廓则可以看作是由齿轮齿廓展成而成的，属于直接包络成形。这类似于用蜗轮滚刀加工蜗轮，而滚刀与蜗杆齿廓相同的情况。

1.1 渐开螺旋齿轮的齿廓方程

齿轮的齿面是右旋渐开螺旋面，它的端截面是渐开线(如图2)，设其基圆半径为rb1，齿槽右侧渐开线ef的起点为e，oe与x1轴的夹角为σ0，渐开线上任意一点M的法线与基圆的切点为a，取∠eoa=u角作为参变数，则渐开线ef的方程式为

把渐开线ef绕z轴螺旋运动，可以得到对应右旋渐开螺旋面的方程为

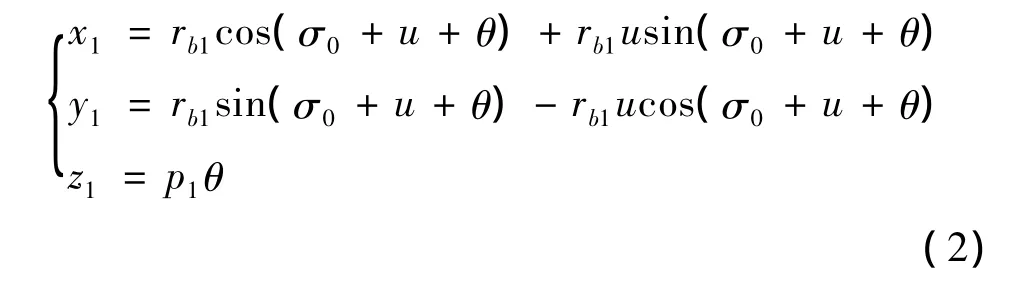
式中，p1是齿轮的螺旋参数，它的意义为端截形渐开线绕z轴转过单位角度时，沿轴线方向移动的距离。对于左旋齿轮，只要把式中p1θ前的正号改为负号即可。θ是参变量，即母线ef从起始位置绕z1轴转过的角度。顺着z1轴看去，以瞬时针方向转动为正。

把式(3)、(4)代入式(2)，可得到齿轮齿槽右侧的齿面方程式为:

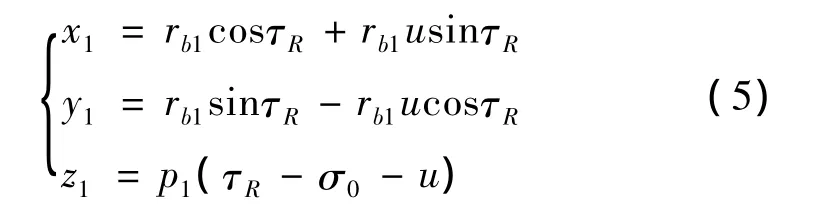
用同样的方法可以求得齿槽左侧的齿面方程。

图3为根据上面推导的公式及表1中的参数完成的渐开螺旋齿轮三维模型。

1.2 变速比齿条设计计算方法

根据齿轮范成加工原理，齿轮加工过程中，齿轮插齿刀和齿轮毛坯按规定的运动做范成运动，插齿刀和齿轮毛坯重合的部分就是被插齿刀切除的部分。即通过插齿刀的齿廓包络出齿轮的齿廓。因此我们只要按照变速比转向器的结构参数建立齿条毛坯和齿轮三维实体模型，根据齿轮齿条的运动关系建立运动仿真模型。这样齿轮和齿条毛坯按规定的变传动比规律做范成运动时，通过计算会生成干涉体，即齿条齿槽切除的部分，也就是加工时插齿刀切除的部分。齿条毛坯减去齿条齿槽切除的部分就得到了我们期望的齿条模型。

2 应用实例

2.1 变速比转向器传动副参数

变速比转向器齿轮齿条副参数见表1所示。

2.2 运动要求

两定速比段的值，从理论上讲，两者相差越多越有利。但由于结构等因素的限制，目前国外选用的速比变化范围均小于30%，如德国ZF公司的产品传动比的变化范围Δi≤26%。它对转向器的性能和传动零件的加工有一定影响。

按汽车转向器的设计要求，齿条沿x方向平移距离σ与设想齿轮按某个瞬时传动比转动一圈(φ=2π)时齿条移动的距离s的关系如图4所示。其中，σ≤σ1时，s=s1;σ≥σ2时 s=s2，传动比为定值;σ1＜ σ ＜σ2，s为半径a的滚圆在s=Q的直线上作纯滚动时，圆内一点(到圆心距离为b)形成的短幅摆线，则

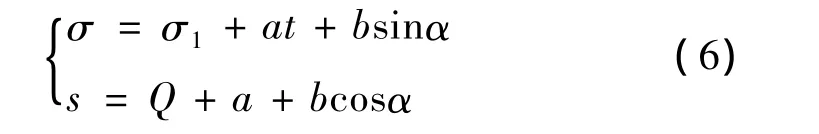
表1 变速比转向器齿轮齿条副参数

σ的负值部分与正值部分对称。已知σ1=5 mm，σ2=60 mm，s1=37.042 mm，s2=29.634 mm。

齿轮齿条的传动比为m(φ1)=ds/dφ，则齿轮转角与齿条位移之间的关系如下

当σ1＜x＜σ2时，α由 x=σ1+at+bsinα使用牛顿迭代法求得。

2.3 变速比齿条的设计计算

根据上述的变速比齿条设计计算方法，按照齿轮齿条参数和运动要求，建立运动仿真模型(如图5)，进行齿条齿廓设计计算。可直接的得到变速比齿条的三维数据模型及齿轮齿条装配模型(见图6，图7)，从图中可以看到，变速比齿条包含完整的齿顶曲线、工作齿廓、过渡曲线及齿根曲线。可以直观地看出:①齿条的齿面是直纹面;②齿条中部的压力角最大，向两端逐渐减小。

根据完成的变速比齿条三维模型，在数控机床上进行了变速比齿扇的加工，这里采用自由曲面的加工方法，图8为完成的变速比齿条的加工样件。对齿轮和变速比齿条的啮合情况进行检验，结果表明齿轮齿条接触区均匀良好，运转灵活平稳;说明变速比齿条齿廓的这种设计计算方法是正确的。

3 结语

本文提出了一种变速比齿条齿廓设计计算的新方法，该方法不使用啮合方程就可以快速而精确地得到变速比齿条的三维数据模型。该方法以齿轮范成加工法为基础，让齿轮根据变传动比运动直接包络出变速比齿条的齿廓。与传统啮合原理的方法和数值计算方法相比，该方法在快速、精确地求解变速比齿轮共轭曲面方面有突出优点，且直接得到了变速比齿条的三维数据模型，该方法简单明了，实用性强;尤其适用于啮合情况复杂，如变传动比共轭曲面的求解。

［1］吴序堂.齿轮啮合原理［M］.北京:机械工业出版社，1982.

［2］吴序堂，王贵海.非圆齿轮及非匀速比传动［M］.北京:机械工业出版社，1997.

［3］贾巨民，张蕾，唐天元，等.汽车变速比齿轮齿条式转向器的啮合原理(Ⅱ)［J］.机械科学与技术，1998(2):191 －193.

［4］候东海，刘忠明，吴序堂，等.交错轴变速比渐开线斜齿轮－齿条传动的啮合分析与加工［J］.机械传动，2001，25(2):20 －25.

［5］李建刚，吴序堂，毛世民，等.非圆齿轮齿廓数值计算的研究［J］.西安交通大学学报，2005，39(1).

［6］毛军红，李黎川，吴序堂，等.变传动比齿条共轭曲面的数值计算方法［J］.机械工程学报，2002，38(5):52 －56.