短链醇、胺和酸等物质水溶液表面张力关联式的新探讨

张文莉 燕云 蒋银花 倪良

(江苏大学化学化工学院 江苏镇江 212013)

水溶液中物质表面张力随浓度的变化主要有3种类型(图1)[1]。对于短链醇、胺和酸等有机物水溶液(图1中曲线Ⅱ)，在低浓度范围内，表面张力随浓度增加明显下降；但在较高浓度范围内，表面张力随浓度增加变化趋缓。根据这一变化，希什科夫斯基提出了一个经验公式：

(1)

式(1)适用的浓度范围较小。为了提高关联精度和提高浓度的适用范围，人们提出了数种表面张力模型或方程，如传统的多项式拟合模型[2]、对数式模型[3]、Gomperty模型[4]和一阶指数衰减函数[5]等。虽然这些数学模型在一定浓度范围内都可用于关联表面张力数据，但由于参数多、物理意义不明确、数学处理又相对复杂，不易推广应用。本文针对短链醇、胺和酸等物质的水溶液，提出一种新的单参数表面张力关联式，通过对部分短链醇、胺和酸等水溶液表面张力数据的考证，说明新关联式的适用性和可靠性。

图1 水溶液中物质表面张力与浓度关系示意图

溶液Ⅰ的表面张力随浓度增加而略有上升，如无机盐、酸和碱等；溶液Ⅱ的表面张力随浓度增加而逐渐下降，如短链醇、胺和羧酸等；溶液Ⅲ的表面张力随浓度增加先急剧下降，到了一定浓度后趋于恒定值，如烷基苯磺酸钠等表面活性剂。

1 表面张力关联式的建立

希什科夫斯基指出，当溶质的浓度很小时，式(1)可简化为：

γ0-γ=ac

(2)

式中c为溶液浓度；γ0和γ分别表示溶剂和溶液的表面张力；a为经验常数，与碳链长度有关。

根据边界条件，c→0，γ→γ0，以及短链醇、胺和酸等物质水溶液表面张力与浓度的变化规律，我们提出以下单参数表面张力公式：

(3)

式中A为大于0的常数，与物质种类有关。式(3)不仅简单，而且计算方便，同时也符合化学学科的惯例。更为突出的一个优点是，可以用一个浓度点的溶液表面张力实验数据来确定方程参数A，从而实现在较大浓度范围内溶液表面张力的预测。

将式(3)两边取自然对数，有:

(4)

2 表面张力关联式的考证

2.1 表面张力随浓度变化趋势的定性说明

将式(4)两边对c求导，得:

(5)

图2 乙醇水溶液的lnγ-c1/2关系曲线

图3 几种物质水溶液的lnγ-c1/2关系曲线

2.2 表面张力数据的关联

本文利用参考文献[4，6]中的乙醇、正丙胺、正丙醇、正丁醇和正己酸等物质的水溶液表面张力数据考核新表面张力关联式的适用性和可靠性。图2和图3是所得结果；表1列出了线性回归所得的相关参数。所得结果可以很好地说明新表面张力关联式具有较大的适用性。

表1 几种短链醇、胺和酸水溶液表面张力与浓度的关联结果

2.3 表面吸附量与浓度的关系曲线

对式(5)作简单整理，可得:

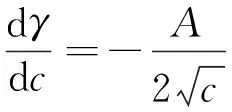
(6)

将式(6)代入吉布斯吸附等温式

(7)

得：

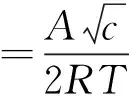
(8)

按式(8)分别求得乙醇、正丙醇、正丙胺、正丁醇和正己酸水溶液的表面吸附量，并作Γ-c图，结果见图4和图5。从图4和图5可知，上述几种物质水溶液的表面吸附量与浓度的关系曲线基本遵循Langmuir吸附等温式。在浓度很低时，式(3)可以简化为希什科夫斯基公式。因此，式(3)也可用于低浓度时表面活性剂水溶液表面张力与浓度的实验数据处理。

图4 乙醇的表面吸附量与浓度的关系

图5 几种物质水溶液的表面吸附量与浓度的关系

3 结论

参 考 文 献

[1] 陈宗淇,王光信,徐桂英.胶体与界面化学.北京:高等教育出版社,2001

[2] 钱蕙,王锡森.铁道师院学报,2002,19(1):61

[3] 向明礼,曾小平,周旭欣,等.实验科学与技术,2004,25(4):1

[4] 朱琳,刘恩,蒋文,等.数理医药学杂志,2008,21(6):647

[5] 周钢,兰叶青,施燕博,等.计算机与应用化学,2007,24(8):1103

[6] 张向宇.实用化学手册.北京:国防工业出版社,1986