非线性脉冲微分方程解析解和数值解的稳定性

郭 爽，张 玲，于 健

(大庆师范学院 数学科学学院, 黑龙江 大庆 163712 )

0 引言

近年来，人们发现许多生物现象的发生以及人们对某些生命现象的优化控制，并非是一个连续的过程，不能单纯地用微分方程或者是差分方程来进行描述。例如在药物动力学中，药物在人身体内的吸收，代谢和排泄等是一个连续过程，可以用一个脉冲微分方程模型进行描述,同时应用脉冲微分方程的理论和方法来研究制订合理用药的最佳方案。

脉冲微分方程对在瞬时干扰下状态发生突然变化的演变过程提供了一种自然的描述。在数学处理上，脉冲的出现使得系统具有混合性，既是连续的，又是离散的。相应的脉冲微分方程理论也比无脉冲的情形要丰富的多。如在不同的脉冲条件下可导致Lorenz系统吸引子的轨道发生本质变化[1], 脉冲也会对其动力学行为产生很大的影响[2]，在脉冲作用下具有时滞的生态模型解的有界性和持久性以及一致持久性都有了一些新的结论[3-4]。脉冲微分方程的研究在生物数学等许多方面的研究中有着广泛的应用。

例1：具有脉冲出生的SIS传染病模型[5]

由于动物的出生率并不是时间的连续函数，多数是以脉冲的形式出现。2004年，文献[5]中刻画了这样的物种遭受传染病的性态而提出该模型。其中N为种群的人口最大容量，S为易患病的种群数量，I为已染病的种群数量，研究他们的基本再生数及其有关的阈值参数，对平衡点的周期解的稳定性进行讨论，而且方法涉及到重合度理论及Lyapunov函数的构造方法，这都是非常有意义的工作。

例2：具有脉冲效应的两个食饵一个捕食者系统模型[6]

种群模型的一个基本问题是研究物种的长期进化行为。自然界中往往是多个种群互相作用而存在的，它们之间的关系就比两个种群时复杂的多。对n维系统的奇点及空间周期解等都是相当复杂的，有可能出现较为复杂的分支现象，也可能有混沌出现。对于具有脉冲效应的种群模型平衡点的全局稳定性和极限环方面已经有了很多较好的工作[7-8]。对于带有扩散系数的脉冲非自治捕食-被捕食系统，通常采用非自治半流的方法来给出一致持久的充分条件和全局存在性条件，同时利用构造Liapunov 函数的方法来证明正周期解的全局稳定性。

我们考虑如下非线性脉冲微分方程解析解和数值解的稳定性：

(1)

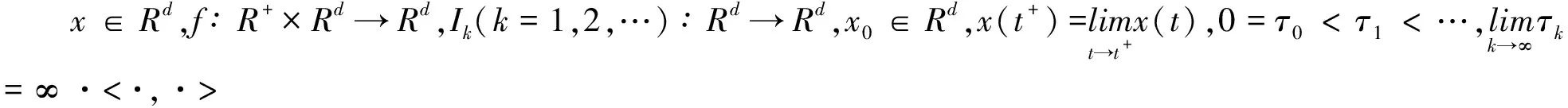
0<θ1≤τk-τk-1≤θ2<∞

下面给出研究问题的Lipchitz条件：

假设满足Lipchitz条件，也就是，存在常数对 ，有

|f(t，x)-f(t，y)|≤L|x-y|

(2)

|Ik(t，x)-Ik(t，y)|≤βk|x-y|

(3)

定义1[7]：如果函数满足下列条件：

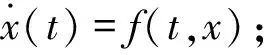
(iii) 函数x(t)在区间(0，+∞)上左连续，且当，t∈(0，+∞)，t≠τk时，x(t+)=Ik(x(t))。则称函数x(t)为方程 (1) 的解。

定义2[8]：如果方程 (1) 对应不同初值的解x1(t)和x2(t)，满足

则称方程 (1) 是渐近稳定的。

定理1[8]： 如果存在实数α，使得对∀x，y∈Rd，有

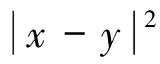
且存在一个常数q∈[0，1]，使得

βjeα(τj-τj-1)≤q<1，j=1，2，…

成立，则方程 (1) 是渐近稳定的。

由定理1可得到下面的推论：

推论1：如果存在常数使得q∈[0，1)，使得

βjeL(τj-τj-1)≤q<1，j=1，2，…

成立，则方程 (1) 是渐近稳定的。

下面是本篇文章的主要结果，给出了解析解和数值解的稳定性结果。

1 数值解的稳定性

我们首先给出方程(1) 的EM方法

(4)

接下来，我们讨论方法(4)的稳定性。为了讨论稳定性，我们考虑方程(1)具有初值扰动的差分格式

(5)

记Xk=(xk，0，xk，1，…，xk，m)T，Zk=(zk，0，zk，1，…，zk，m)T。

我们下面给出方法(4)的稳定性的定义：

定义3：EM方法(4)被称为是渐近稳定的，如果存在常数M，使得对任意给定的x0，z0及所有的正整数m>M，Xk和Zk满足：当k→∞时

|Xk-Zk|→0

(6)

证明：记

利用内积的性质，有

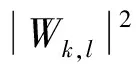
(7)

由条件(2)，可得

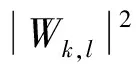
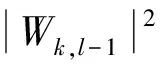
(8)

两边开方，得

|Wk，l|=(1+hkL)|Wk，l-1|

(9)

从而，我们得到

|Wk，l|=(1+hkL)l|Wk，0|

(10)

利用条件 (3) 得到

(11)

|Wk，l|≤((1+hkL)mβ)k(1+hL)l|W0，0|

(12)

观察式(11)，不难发现，当(1+hkL)mβ<1时，|Wk，l|→0，k→∞。定理证完。

2 数值算例

下面给出一个例子来验证我们的结论

例 1：

(13)

可以验证方程 (13) 都满足条件推论1的条件。运用步长h =1/m (m=30)，我们用EM方法求方程 (13) 的数值解，得到图1。从这个图中可以看出，数值解是渐近稳定的。

图1 方程 (13) 的数值解

3 结语

综上所述，我们主要研究了非线性脉冲微分方程解析解和数值解的稳定性，在Lipchitz条件下得到了解析解的稳定性和EM方法的数值解的稳定性，最后给出一个例子来验证结果。从例子中可以看出，数值解是渐近稳定的。这为以后我们继续研究脉冲微分方程解析解和数值解的性质奠定了坚实的基础并提供有力的理论根据。

[参考文献]

[1] V. Lakshmikantham, D.D. Bainov. Theory of Impulsive Differential Equantions[M]. Singapore:World Scientific,1989.

[2] A. Michel, K. Wang. Qualitative Analysis of Cohen-Grossberg Neural Networks[J]. Neural Networks,2002，15: 415-422.

[3] Y.Kuang,Delay differential equations with applications in population dynamics[M].New York:cademic Press,1993.

[4] F.Zhang,Z.Ma ,J.Yan,Functions boundary value problem for first order impulsive differential equations at variable times[J].Indian J.pure Applied Math.,2003,34:733-742.

[5] 马知恩.种群生态学的数学模型与研究[M].合肥:安徽教育出版社，1994.

[6] D.D. Bainov, P.S. Simeonov. Systems with Impulse Effect: Stability, Theory and Applications[M]. Ellis Horwood： Chichester, 1989.

[7] Y.J. Zhang, B. liu, L.S. Chen. Extinction and Permanence of a Two-Prey One-Predator System with Impulsive Effect[J]. Math. Med. Biol. 2003, 20: 309-325.

[8] Lakmeche A，Arino O..Bifurcation of non trivial periodic solutions of impulsive differential equations arising chemotherapeutio treatment,Dynam-ics of Continuous[J].Discrete and Impulsive system,2000,7:265-287.