基于压力的速率方程的应用
杨鹏辉
(西安石油大学化学化工学院 陕西西安 710065)
在动力学中,对于一般的恒容反应,通常使用基于浓度的速率方程;只有对于气相反应,才可以使用基于压力的速率方程。故一般教材中只注重讨论基于浓度的速率方程,而对于基于压力的速率方程则讨论较少,造成学生在解题和应用中的困惑。事实上,对于气相反应,测定系统压力很方便,基于压力的速率方程中的参变量为p0,p,使用基于压力的速率方程解题比使用基于浓度的速率方程更直接,更简便。下面以一道例题来说明这一点。
例500K时,在一抽空容器中引入气体A进行如下二级反应:

已知:反应开始时容器内总压p0=4.52kPa,反应进行300s后,总压降为2.92kPa,求速率常数kp,A,kA及多少秒后系统总压降至2.70kPa。
解一:设300s时,A(g)的分压为p。

p00
p0.5(p0-p)
由p+0.5(p0-p)=0.5(p0+p)=2.92kPa,
可以解得:
p=1.32kPa
使用基于压力的速率方程
代入数据,可以解得:
kp,A=1.788×10-3kPa-1·s-1
k=kp,ART=7.434 L·mol-1·s-1
系统总压降至2.70kPa时,A(g)的分压
p=0.88kPa
将p0,p,kp,A代入基于压力的速率方程,可以解得:
t=511.8s
cA,00
cA0.5(cA,0-cA)
由p0=cA,0RT=4.52kPa,(cA+0.5(cA,0-cA))RT=0.5(cA,0+cA)RT=2.92kPa,得:
cA,0=1.087×10-3mol·L-1
cA=3.175×10-4mol·L-1
使用基于浓度的速率方程
代入数据,可以解得:
k=7.432 L·mol-1·s-1
kp,A=k/RT=1.788×10-3kPa-1·s-1
系统总压降至2.70kPa时,由
0.5(cA,0+cA)RT=2.70kPa
可以解得:
cA=2.119×10-4mol·L-1
将cA,0,cA,k代入基于浓度的速率方程,可以解得:
t=511.2s
通过以上例题可以看出,对于同一气相反应,使用基于压力的速率方程和基于浓度的速率方程解出的结果是一致的。基于压力的速率方程中参变量为p0和p,解题时不必导来导去,比使用基于浓度的速率方程更直接,更简便。
一般教材中都总结了具有简单级数的反应的基于浓度的速率方程及其特征,而未讨论基于压力的速率方程。为了便于理解记忆和使用,现对具有简单级数的反应的基于压力的速率方程的微分式、积分式及直线关系进行总结,并列于表1。
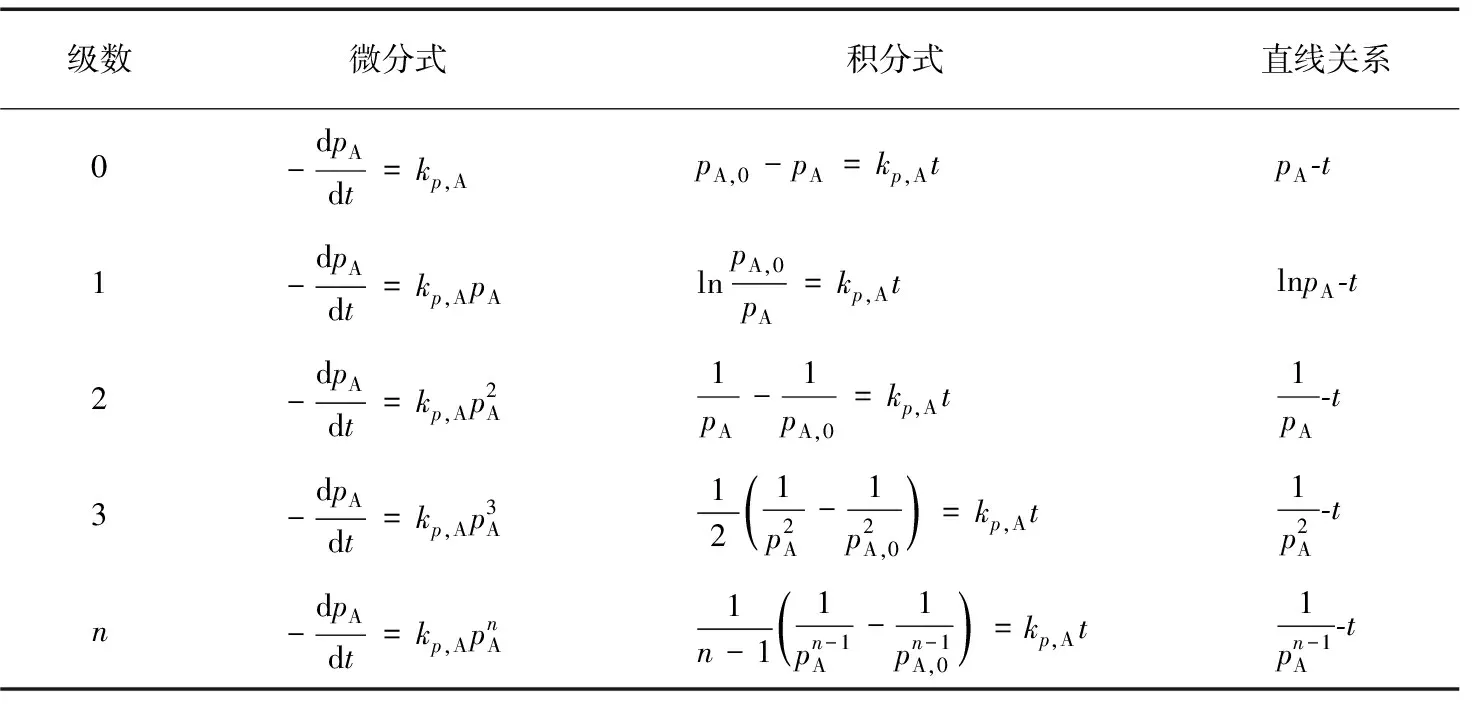
表1 具有简单级数的反应的基于压力的速率方程及其特征
[1] 傅献彩,沈文霞,姚天扬,等.物理化学.第5版.北京:高等教育出版社,2005
[2] 李松林,周亚平,刘俊吉.物理化学.第5 版.北京:高等教育出版社,2009
[3] 胡英,吕瑞东,刘国杰,等.物理化学.第5 版.北京:高等教育出版社,2007

