有关固体颗粒分散度与化学反应平衡常数关系的探讨*

周宇行 王旭珍 靳长德

(1 大连理工大学化工与环境生命学部化工学院2008级 辽宁大连 116024；2 大连理工大学化工与环境生命学部化学学院 辽宁大连 116024)

在表面化学有关知识的习题中，有这样一道题：“对于热分解反应CaCO3(s)=CaO(s)+CO2(g), 在一定温度下达到平衡，若保持其他条件不变的情况下，将CaCO3(s)由块状破碎为粉末状时，分解压如何变化？”

解答是：“CaCO3(s)粉碎后表面能增大，化学势增高，平衡右移，KӨ变大，故分解压(p(CO2))也变大”。

虽然读者能够理解答案所蕴含的道理，但对于这样一个体系，从固体颗粒的大小(分散度、表面能)，关联到平衡常数与分解压，思维会有一些跳跃性。笔者意识到，这个例题应该是一个好题目，它提示我们：在化学热力学部分重点讨论过的通常只涉及无非体积功、双变量系统的平衡常数表达式(即不考虑界面能贡献的关系式)，当面对高度分散系统时，需要考虑分散度(或表面能)的影响，即需要将分散度作为变量,重新推导多组分多相反应系统平衡常数的表达式。在此，尝试推导如下。

我们知道，对于化学反应，考虑相界面与不考虑相界面时,化学平衡判据的形式一致[1]，即：

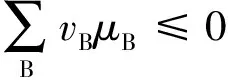
(1)

对于固态纯物质和理想气体的复相反应aA(s)+bB(g)=yY(s)+zZ(g)，各物质的化学势表达式分别为：

其中，后两个固体纯物质的化学势表达式推导如下：

对于纯固体体相，化学势只是温度、压力的函数[1-5]：

dμ=-SmdT+Vmdp

但对于高度分散系统，表面张力对固相产生的附加压力不能忽略，故定温下有：

这里认为p≈pӨ且固体不可压缩。对于各向同性的固体，其附加压力与液滴的类似(两者区别可参考文献[6])，即：Δp=σ(dAs/dV)；对于半径为r的球体来说，dAs/dV=2/r，分散度aV=As/V=3/r，故：

将上述各物质的化学势表达式代入式(1)，应用于球状颗粒可得:

(2)

达到平衡时，∑vBμB=0，则有:

(3)

又由标准平衡常数的定义[2]:

即有:

(4)

将式(3)两边同除以RT代入式(4),整理可得:

(5)

由式(5)可知，若不考虑分散度的影响，即aV,B=0，则有:

(6)

即KӨ=K′，显然，式(6)与通常物理化学教材中化学平衡章节推导的平衡常数表达式完全一致。

若考虑分散度的影响，则有：

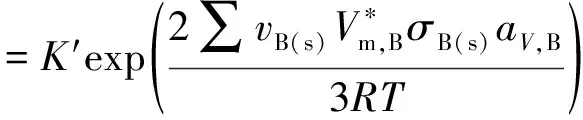
(7)

由此可以清楚地看出是否考虑分散度情况下表观平衡常数K′的差别。

基于式(7)，结合前面的例题，假定在一定温度下已达平衡的复相反应系统中产物CaO(s)颗粒的分散度不变，只考虑CaCO3(s)固体(v(CaCO3)=-1)由大颗粒粉碎为小颗粒并视为球体，由式(7)可知，此时分散度的改变对平衡常数的影响为：

(8)

因lnKӨ=f(T)，定温下有定值，故有：

[1] 胡英.物理化学.第4版.北京:高等教育出版社,2005

[2] 傅玉普,王新平.物理化学简明教程.第2版.大连:大连理工大学出版社,2007

[3] 王正烈,周亚平,李松林，等.物理化学.第4版.北京:高等教育出版社,2001

[4] 傅献彩,沈文霞,姚天扬，等.物理化学.第5版.北京:高等教育出版社,2005

[5] 韩德刚,高执棣,高盘良.物理化学.北京:高等教育出版社,2001

[6] Cammarata R C.ProgSurSci,1994,46(1):1