基于小波的改进加权抛物线插值的图像超分辨率算法

蔡 念， 张海员， 张 楠， 潘 晴

（广东工业大学信息工程学院，广东 广州 510006）

基于小波的改进加权抛物线插值的图像超分辨率算法

蔡 念， 张海员， 张 楠， 潘 晴

（广东工业大学信息工程学院，广东 广州 510006）

为了尽可能地保持图像的基本信息，提高图像的视觉效果和空间分辨率，提出一种基于小波的改进加权抛物线插值算法，即在传统的加权抛物线算法上增加插值的误差补偿项。利用sobel算子设定插值点的边缘方向，得到初始放大图像。利用小波变换提取高频成份，原始图像幅值增强充当低频部分，再经过小波逆变换得到高分辨率图像。实验结果表明，相对于传统的图像放大算法，该算法考虑到全局相关性，得到更加清晰的边缘信息。

图像放大；小波变换；误差补偿；超分辨

图像插值是在不改变信息采集物理系统的前提下，利用低分辨图像获得高分辨率的图像。图像插值在遥感卫星，气象，医学成像，电影制作，军事等方面有着广泛的应用。图像插值放大可以增加数据量，但不能增加信息量，图像放大技术只是为了改善图像细节部分和空间分辨率[1]。

传统的插值方式有最近邻点插值，双线性插值，和双三次插值等[2-3]，这些方法均能实现图像放大，但不能很好地抓住图像的边缘，亦未能考虑到图像的边缘与纹理方向，使得插值后的图像边缘模糊，有明显的锯齿现象，影响视觉效果。为了得到更好的边缘信息和纹理特性，Li等[4]提出了以边缘为方向(new edge-directed interpolation,NEDI)，利用邻域统计和边界信息进行插值。Cha[5]提出了一种基于双线性插值误差补偿(edge-amended sharp edge, EASE)的图像放大技术，该算法具有各向异性和边缘自适应性，对双线性插值进行误差补偿，在边缘保护方面明显优于经典插值方法。Liu[6]等提出了一种基于小波的双线性插值迭代算法，利用被插值图像像素点的全局相关性与高频外推的原理实现插值。尽管这些方法能得到较清晰的纹理和边缘，但是对于纹理细节丰富的图像，不能体现出优越性。

传统插值方法与Li，Cha等人只考虑了被插值图像局部像素点之间的关联性，未考虑被插值图像的全局相关性，将损坏图像的高频细节部分。近年来，图像边缘方向估计已成为图像插值研究的热点[6-7]。尤其小波变换能够有效地估计边缘方向，改善图像的细节部分，因此小波理论在图像插值领域得到了广泛的应用[8-10]。本文对传统的加权抛物线插值算法进行误差补偿，结合小波变换，充分利用被插值图像像素点的全局相关性，提出一种基于小波的改进加权抛物线插值的图像放大算法。

本文首先介绍经典插值方法和插值误差理论、利用拉格朗日插值和牛顿插值推导插值误差补偿项。其次，由一维信号的二倍插值出发，对抛物线插值的误差补偿项进行数学推导，进而推广到任意倍数的放大；在对二维信号进行插值误差补偿时，借助于一维信号的插值方式，先对原二维信号的行和列进行插值点估计，对于不在原图像行列上的点，借助sobel算子自适应估计。最后，为了利用全局相关性，采用自适应幅值增强的原始低分辨率图像充当低频部分，进行小波逆变换，得到重构高分辨率图像。改进的加权抛物线插值算法结合小波算法进行超分辨率重建，改善了图像的细节部分，重建后的图像能够有效地保持原始图像的高频细节，同时也提高了图像的空间分辨率。重建后的图像更有利于人眼观察的最佳图像。

1 经典插值方法及误差补偿理论

图像插值可以理解为利用插值点周围的邻域像素点，加权估计位置插值点的灰度值[11]。最近邻点插值法将采样插值点邻近4点中距离最近点的像素值作为插值点的像素值。双线性插值法利用插值点周围的4个邻近点加权内插作为该点的灰度值[2]，插值点f(i+u,j+v)可表示为

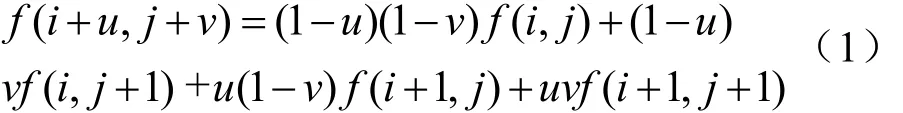
其中，f(i,j)为图像在(i,j)处的灰度值，u、v为插值点距离(i,j)点的水平和垂直距离。双三次插值方法先对图像以行为方向，每4点为插值点进行三次插值，再以列为方向，每4点为插值点进行三次插值。

经典的图像插值方法源于拉格朗日插值方法和牛顿插值方法。设函数y=f(x)在区间[a, b]上有定义，在插值区间[a,b]，点x0，x1，…,xN为不同的插值节点，假设f(N+1)(x)对于任意的x∈[a,b]存在，利用N阶插值多项式pN对函数f(x)进行插值，对于任一个x∈[a,b]，都有一个点ξ∈[a,b]使得

假设插值节点为均匀分布，并对于任意的M＞0 均有 maxx∈[a,b]|f(N+1)(x)|≤M, 则有

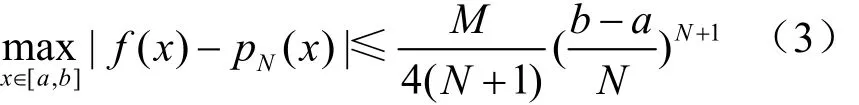
当N=1时，为两点x0，x0+h之间的线性插值，在此两点之间存在一个点ξ，使得

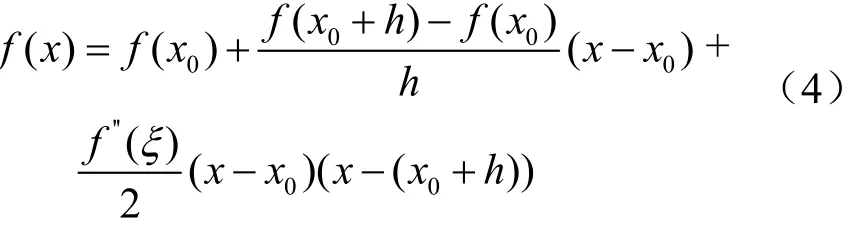
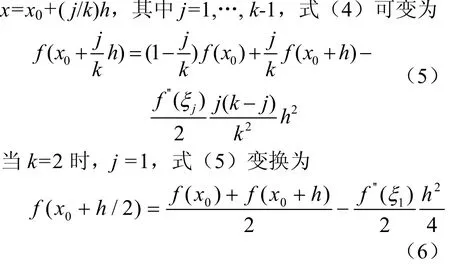
式(6)是线性插值的表达式。

当N=2时，为三点xi-1，xi，xi+1（xi-1＜xi＜xi+1,间距为h）之间的二次插值，插值节点为x∈(xi-1,xi+1)，则插值函数可以表示为

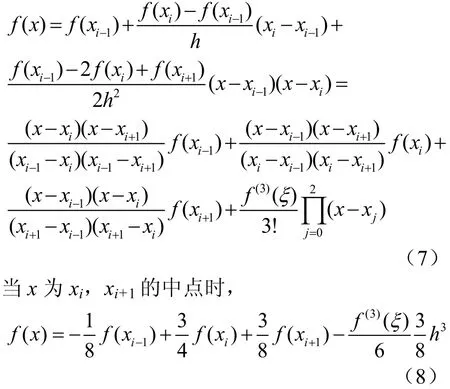
式(8)为抛物线插值的表达式。

2 加权抛物线插值误差补偿理论

2.1 加权抛物线插值

抛物线插值是经过相邻三点做一条二次曲线。假设存在已知函数y=f(x)，在相邻两点之间做插值，可以做出两条不同的曲线，用加权方法融合两条曲线做一条插值曲线。假如在x1,x2之间插入一点x，可以选择x0,x1,x2和x1,x2,x3做插值曲线，其插值曲线分别为

2.2 抛物线插值误差补偿理论

2.2.1 一维信号的误差补偿

假设存在一维信号f，在其中选取点x∈(xi,xi+1)，如图1，为了简明，先设定x为xi,xi+1的中点，即x=(xi+xi+1)/2。

图1 一维信号的误差补偿

假设对于任意的i,xi+1-xi=2，则式（7）变为

其中，ξ∈(xi,xi+1)，该误差补偿项是为了修补图1中“○”和“□”之间的距离。因为ξ是一个未知量，所以该补偿项无法直接计算。将xi设为xi-3,xi-1,xi+1的插值项，对于插值点xi的误差补偿项，作如下定义

其中，ξ1∈(xi-1,xi+1)，假如f(3)在(xi-3,xi+1)中变化不大，则通过式(15)和式(18)可以得到：Ri+1/2=(1/8)RL。

在假定三阶导数f(3)在信号光滑区域变化不大的前提下，可以得到一维信号的抛物线误差补偿的公式如下（以放大两倍为例）

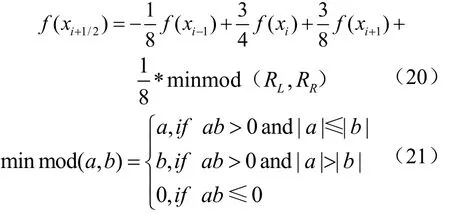
minmod这个函数决定了误差修补的方向[5]。当RL,RR具有不同的符号的时候，说明在区间(xi,xi+1)存在着边缘信息或者是转折点；在两者是同符号的时候，选取比较小的一个做误差补偿。这样，抛物线插值误差补偿就能较好地估计f(xi+1/2)。

综上，对于一维信号的抛物线误差补偿表达式可以归结如下，假如将(xi,xi+1)区间分为k段，j=1,…,k-1,

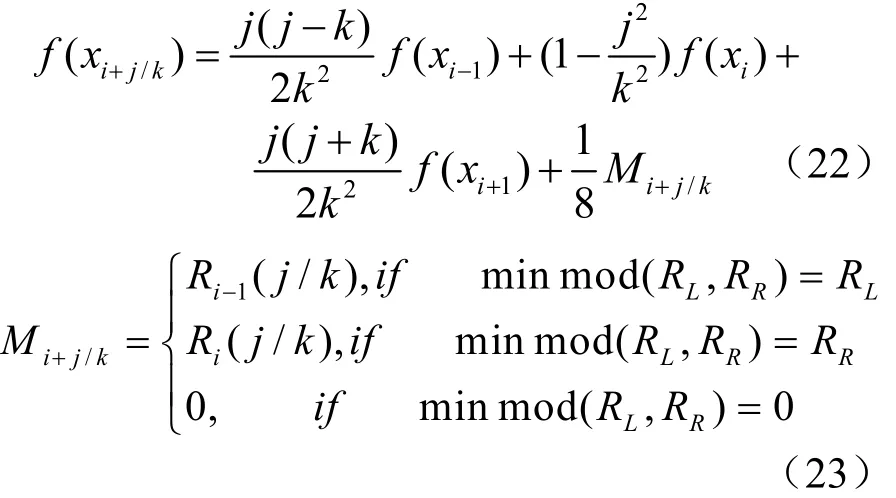
其中Mi+j/k定义为在区间(xi-3,xi+1)中公式(8)与抛物线插值间的差值，估计点设为：xi-3+(j/k)*4h

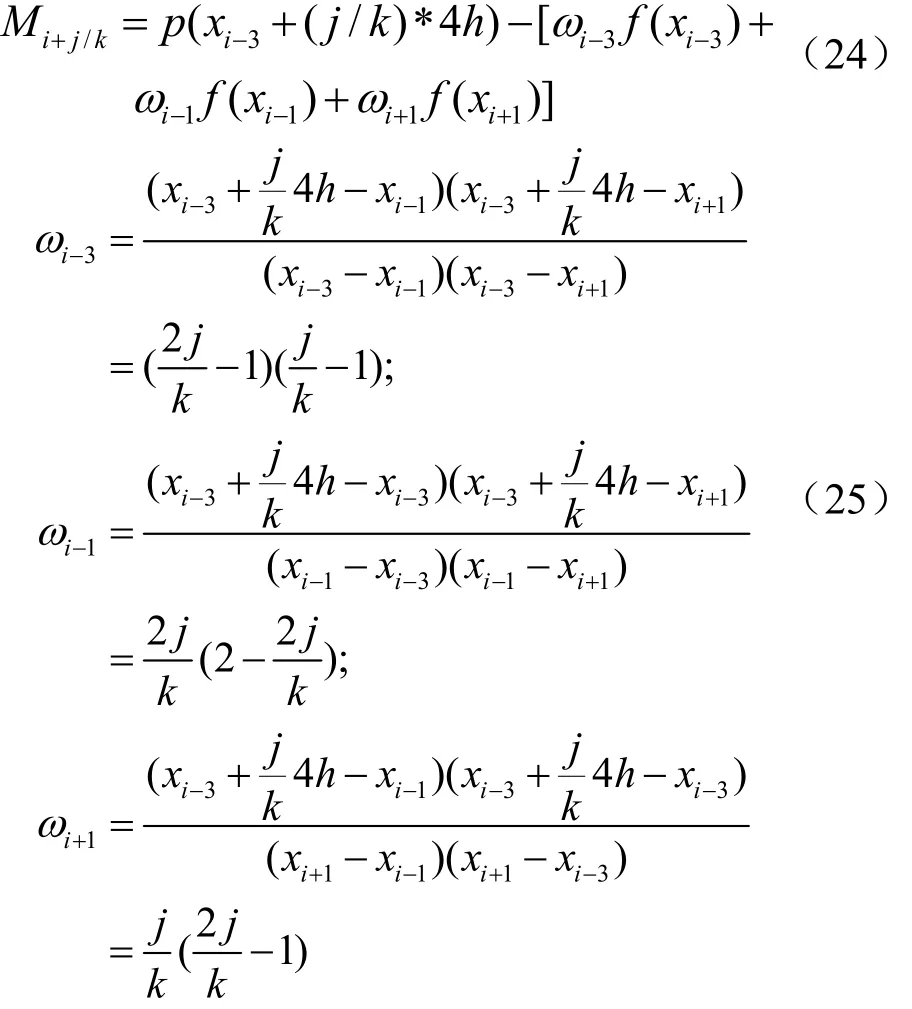
2.2.2 二维图像的误差补偿

图2展示了一幅图像的二倍放大，实心点表示低分辨率图像的像素点，通过一维信号的抛物线插值误差补偿方法可以得到“□”的值，在计算出所有的“□”点之后，采用边缘自适应的方法估计出中心“○”的值。为了估计边缘方向，首先计算4个方向sobel算子的绝对值[5]

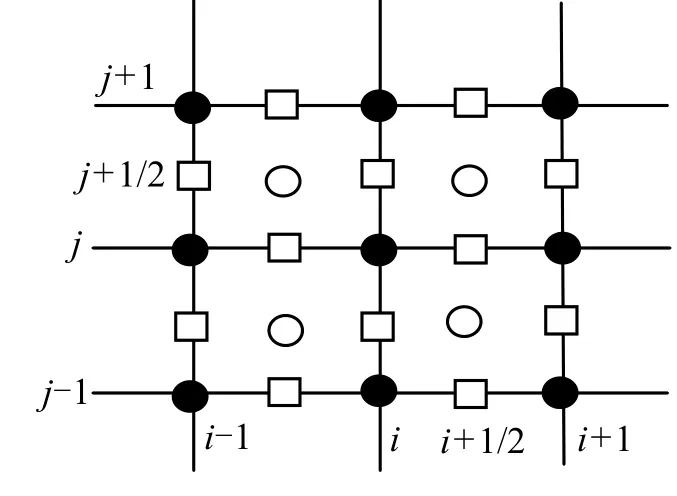
图2 二维信号二倍放大的误差补偿示意图

假设图像的边缘具有局部双线性，可以得出边缘方向是在最小的两个sobel算子之间，并且更小的两个方向是毗邻的，相差 45º。用Sp,Sq代表较小的两个sobel算子值，分别是水平/竖直方向和 45º/135º方向

则中心“○”点的计算公式可以定义[5]为

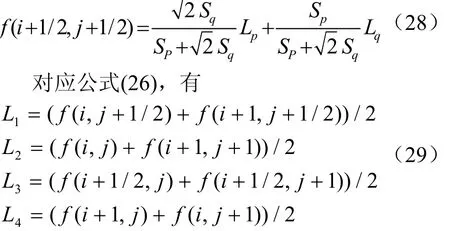
3 二维离散小波变换

将一维小波变换推广到二维小波变换，可以简单地理解为将二维小波写成两个一维小波变换的乘积。Mallat提出了小波的快速分解和重构的算法[12-13]。其原理是：快速小波分解利用两个一维滤波器对二维图像实现，图像重构是利用分解时的两个一维滤波器的镜像滤波器。分解过程为

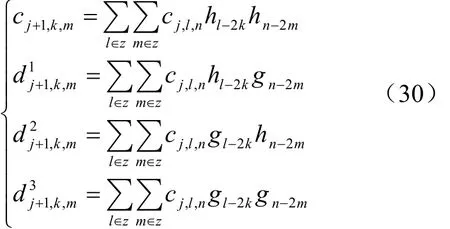
4 算法描述

1） 利用加权抛物线插值误差补偿算法对原始低分辨率图像进行插值放大，得到图像I1。

将图像进行插值放大，在原图像行或列上的点利用式(20)进行插值放大，对于对角线上的点利用式(28)进行估计。

2） 对图像I1进行小波变换分解。本文采用sym4小波变换，得到一个低频部分，3个高频部分。一次小波分解为

3） 对于I1图像小波分解之后的高频成分I1H、I1V、I1D保留不变；对原始低分辨率图像进行线性变换，利用低频部分I1L的小波系数和I1的数值关系，自适应幅值增强,得到新的低频部分I2L。

4） 利用新得到的低频部分和I1图像小波分解之后的高频成分进行小波逆变换得到图像I3

5 实验结果

为了证明基于小波的改进加权抛物线插值误差补偿算法的优越性，本文分别对纹理简单的人工合成图像，纹理中等的 Lena图像，纹理较复杂的猴脸图像（图3），进行了NEDI放大，EASE放大，小波双线性，小波加权抛物线插值误差补偿放大（本文实验以 2×2放大为例，详见图 4～图 6）。

图3 样本图片

为了比较采用不同放大方法得到的图像，避免过多的主观因素，本文采用平均梯度和信息熵来定量分析图像放大后的效果。平均梯度T的定义为

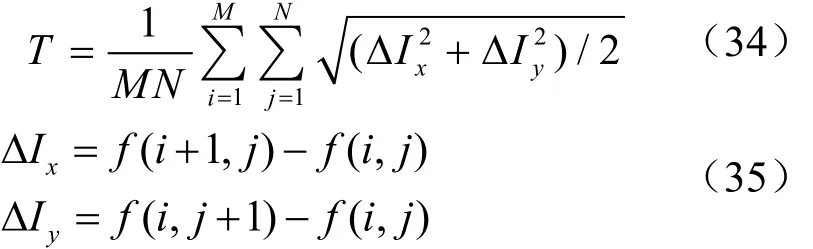
其中，M,N是指图像f的长与宽。平均梯度能很好的反应图像的纹理信息及边缘清晰度。

信息熵反应图像包含信息量的多少，反应细节的丰富程度，定义如下

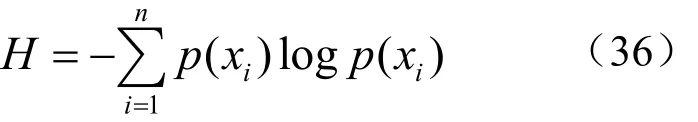
图4 人工合成图像的放大图像

图5 lena图像的放大图像

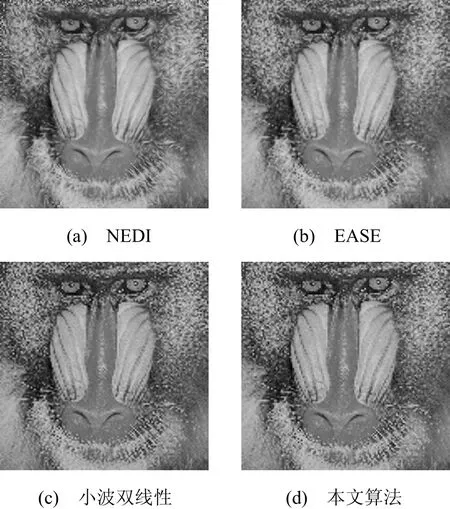
图6 猴脸图像的放大图像

由图4～图6可以看出，EASE考虑了边缘的方向，能得到较好的边缘信息，但是未考虑像素点的全局相关性。小波双线性插值考虑了像素点的全局相关性，提高了图像的空间分辨率，但是在边缘方向估计上缺少自适应性。本文算法对加权抛物线插值的误差项进行自适应修补，并借助小波利用了像素点的全局相关性，可以得到清晰的纹理细节，从而提高图像的视觉效果。因此，在直观视觉上看，本文算法明显优于EASE，与小波双线性差别不大。

通过定量分析（见表1）可以看出，本文算法得到的平均梯度远大于其他算法，更能反映图像纹理特征的变化。对于纹理越复杂的图像，该算法更能体现出优越性。

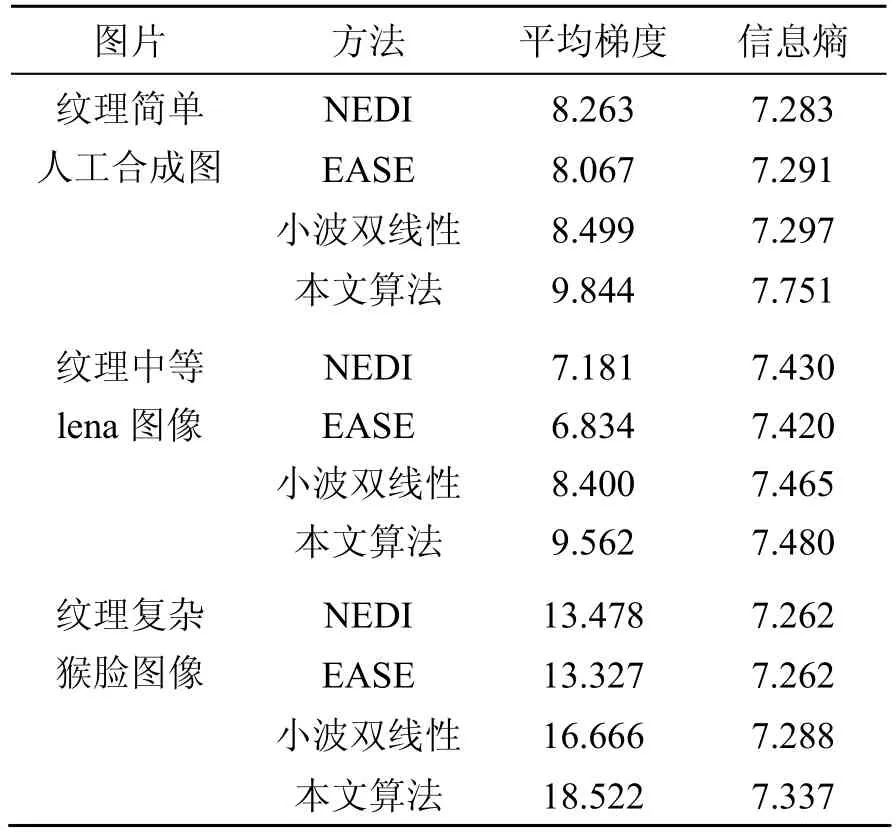
表1 图像放大效果客观评价

6 结 论

本文提出一种改进的加权抛物线插值算法，并结合小波算法进行超分辨率重建，提高了图像的平均梯度，得到了更好的图像的空间分辨率、纹理信息和边缘清晰度；相比于其他图像放大算法，本文算法能获得更高的信息熵，减少了图像基本信息的损失。本文算法放大倍数灵活，可以一次得到任意倍数放大的图像。实验结果表明，该算法优于传统的插值算法，可以广泛应用于计算机制图，遥感图像处理等图像放大领域。

[1]刘志刚, 刘代志. 基于小波变换的图像放大方法再讨论[J]. 中国图象图形学报, 2003, 8A (4)：403-408.

[2]Castleman K R. Digital Image Processing [M]. Engle Cliffs, NJ：Prentice Hall, 1996.

[3]Parker J A, Kenyon R V, Troxel D E. Comparison of interpolating methods for image resampling [J]. IEEE Trans. Medical Imaging, 1983, 2 (1)：31-39.

[4]Xin Li and Michacl T. New edge directed interpolation [J].IEEE Trans. Image Processing, 2001, 10(10)：1521-1527.

[5]Youngjoon Cha and Seongjaj Kim. The error-amended sharp edge (EASE) scheme for image zooming [J].IEEE Trans. Image Processing, 2007, 16(6)：1496-1505.

[6]Min Li, Truong Q Nguyen. Markov random field model-based edge-directed image interpolation [J].IEEE Trans. Image Processing, 2008, 17 (7)：1121-1128.

[7] Chuanbai Xiao, Yanchao He, Jing Yu. A highefficiency edge-preserving Bayesian method for image interpolation [C]//ICSP2008, 2008：1042-1046.

[8]Liu Bo, Qu Youshan, Feng Guilan, etal. Maximal PSNR wavelet bi-linear interpolation iterative algorithm in remote sensing image [J]. ACTA Photonica Sinica, 2006, 35(3)：468-472.

[9]Temizel A and Vlachos T. Wavelet domain image resolution enhancement [J]. IEEE Proceedings-Vision and Signal Proceedings, 2006, 153(2)：25-30.

[10]Xiongbo Zheng, Xiaowei Zhang, Zhijuan Weng. A novel multiwavelet-based interpolation algorithm of images [C]//2009 Int. Conf. Wavelet Analysis and Pattern Recognition, Baoding, 2009：281-286.

[11]程光权, 成礼智. 基于小波的方向自适应图像插值[J].电子与信息学报, 2009, 31(2)：265-269.

[12]Mallat S G. A theory for multiresolution signal decomposition：the wavelet representation [J]. IEEE Trans. Pattern Analysis and Machine Intelligence,1989, 11(7)：674-693.

[13]Jo Y T, Shen L X, Seng L L, et al. A general approach for analysis and application of discrete multi-wavelet transform [J]. IEEE Trans. Signal Processing, 2000,48(2)：457-464.

Using improved weighted parabolic interpolation and wavelet transformation to zoom images for super-resolution

Cai Nian, Zhang Haiyuan, Zhang Nan, Pan Qing
( School of Information Engineering, Guangdong University of Technology, Guangzhou Guangdong 510006, China )

In order to preserve the basic information of images and to improve their visual performance and space resolution, a novel image zooming algorithm is proposed by using improved weighted parabolic interpolation and wavelet transformation which incorporates the error-amended part into the classical weighted parabolic interpolation algorithm. Directions of interpolation points are determined by the Sobel operator, then a preliminary zoomed image is obtained. High-frequency components are got by a wavelet transformation, and low-frequency components are replaced by the enhanced amplitude of the original image. At last, a high-resolution image is achieved by inverse wavelet transformation. The experimental results indicate that, compared with traditional image zooming algorithms, this algorithm can get clearer and sharper edges due to considerations of global pixels correlation of the original image.

image zooming; wavelet transformation; error-amended sharp edge scheme;super-resolution

TP 391

A

1003-0158(2012)01-0050-06

2010-05-14

国家自然科学基金资助项目（61001179）；广东省自然科学基金资助项目（07301038，9451009001002667）

蔡 念（1976-），男，安徽马鞍山人，副研究员，博士后，主要研究方向为图像处理、模式识别等。