基于根轨迹校正法的倒立摆控制系统设计

杨世勇，张景辉，谭 翚

（烟台大学计算机学院，山东烟台264005）

1 引言

在经典控制理论中，根轨迹法是一种分析和设计线性定常系统的图解方法，由于它具有方便快捷的特点，已经成为经典控制理论中最基本的方法之一。关于根轨迹法校正，有不少文献给出了较详细的介绍［1、2]，还总结出了一些具体实现方法，如几何法、解析法等，它们的校正补偿器都采用固定的结构模式。然而，实践中控制对象通常是较复杂的，因此在实际的控制系统设计时，校正补偿器有时不必拘泥于采用某种固定的模式，而应该以达到预期的性能指标为目的，方法越简单越好。倒立摆是自动控制领域典型的控制对象，经常用来研究和检验控制策略与方法［3] ［4]。本文以直线一级倒立摆为研究对象，采用一种根轨迹校正法，无须繁琐的几何作图和复杂的数学解析，仅需遵循绘制根轨迹的基本原则和一些定性的分析，便完成了控制系统的设计，达到了预期的性能指标，方法简单、快捷，对于高阶控制系统的设计具有一定的参考价值。

2 控制对象的建模及其分析［3] ［4]

若忽略各种阻力和摩擦力，可将直线一级倒立摆抽象成小车和均匀质杆组成的系统，如图1所示。

图1 倒立摆示意系统

图中小车质量 M＝1.096kg，摆杆质量 m＝0.109kg，半杆长l＝0.25m，小车摩擦系数b＝0.1N／m／sec，摆杆转动惯量 I＝0.0034kgm2，重力加速度g＝9.8m／s2，φ 是摆杆与垂线向上的夹角（rad），x是小车的水平位移（m），u是加在小车上的控制。倒立摆是一个多变量系统，而经典控制理论研究的对象主要是单输入单输出的系统，因此本文只探讨对摆杆角度的平衡控制问题。运用牛顿力学定律建立系统的运动方程，消掉中间变量，将方程在平衡点（φ＝0，x＝0）附近线性化处理，经过整理后可以得到以控制u为输入、摆杆角度φ为输出的倒立摆对象开环传递函数为：

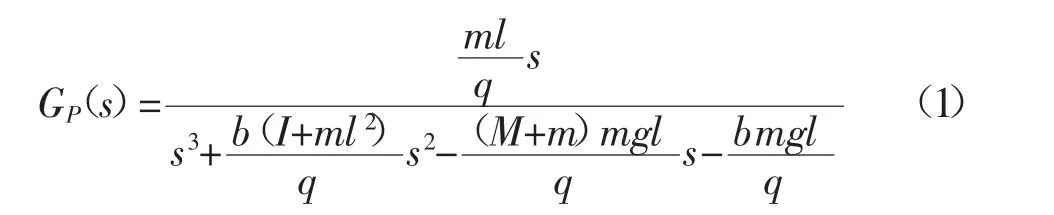
其中 q＝［（M+m）（I+ml2）-（ml）2]

代入实际参数后：

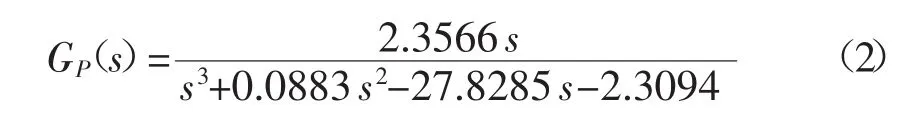
对控制对象的模型分析如下：

（1）开环零极点

一个零点：z0＝0（原点处）；

三个极点：p1＝-5.2780，p2＝-0.0830，p3＝5.2727（在右半平面）。

（2）校正前开环传递函数的根轨迹如图2（a）所示，由于存在一个右极点，系统肯定不稳定，其脉冲响应如图2（b）所示。

3 根轨迹法的控制系统设计［5] ［6]

控制系统原理如图3（a）所示，在图中输出被控量y为摆杆与垂直线的夹角，输入给定r＝0，即摆杆垂直角度的控制目标为零，f是对系统施加的脉冲扰动，u是加在小车上的控制。考虑到给定r＝0，原理图变换成图 3（b）所示。

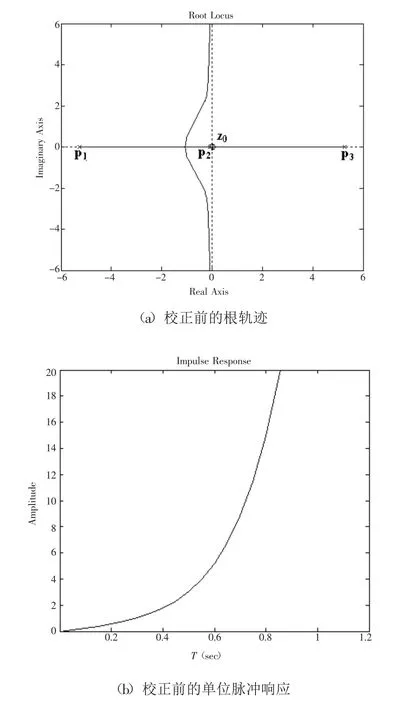
图2 校正前系统的根轨迹及脉冲响应

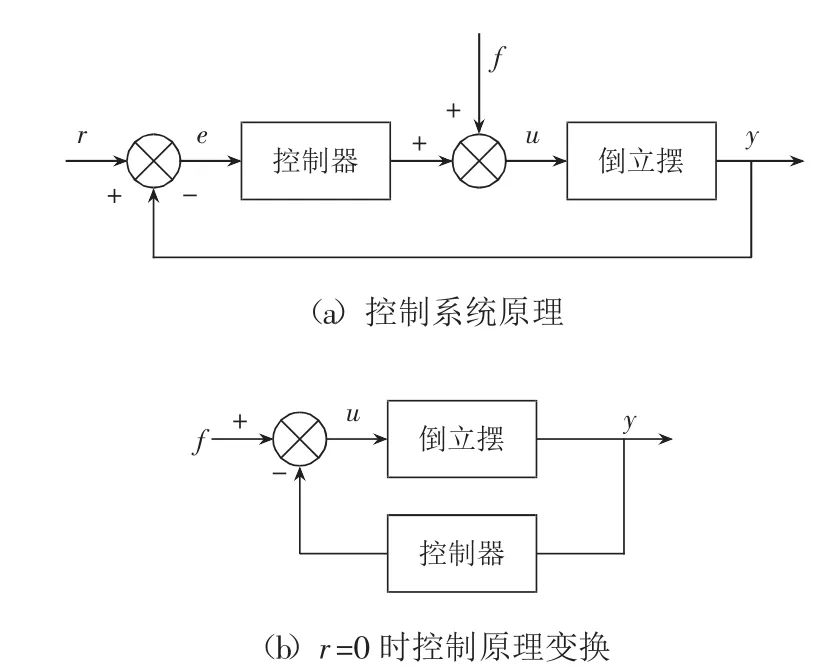
图3 基于根轨迹法校正的原理图

系统设计的性能指标要求为：试设计控制器以产生合适的控制u，使得摆杆能够克服外界脉冲扰动f的影响，以较小的超调量σ%＜1.5%，较短的调节时间ts＜2s恢复到垂直平衡的位置。根轨迹法控制器设计的基本思想是借助根轨迹曲线进行控制系统的校正设计。由于决定系统性能的主导极点往往不在系统的根轨迹上，而添加开环零点或极点可使根轨迹曲线发生改变，因此只要在s平面恰当的位置增添开环零点或极点，使得闭环系统根轨迹出现的方位和形状朝有利于性能提高的方向变化，就能够达到期望的性能指标要求。下面将详细介绍校正设计的全过程。

第1步：在原点处添加一个极点p0＝0，抵消掉原点处的零点z0＝0。这是对图2（a）的根轨迹图分析后采取的初步策略。这时根轨迹变为图4，还剩下三个极点：p1＝－5.2780，p2＝－0.0830，p3＝5.2727，它们是对应的三条根轨迹的起点，其中第一条起于p1，在负实轴上向左终止于无限远处，而后两条根轨迹在正实轴上会合后分别向上向下分离，并分别沿着与正实轴成±60度的两条渐近线，向右半平面终止于无限远处，它们永远不会到达左半平面，系统不会稳定。

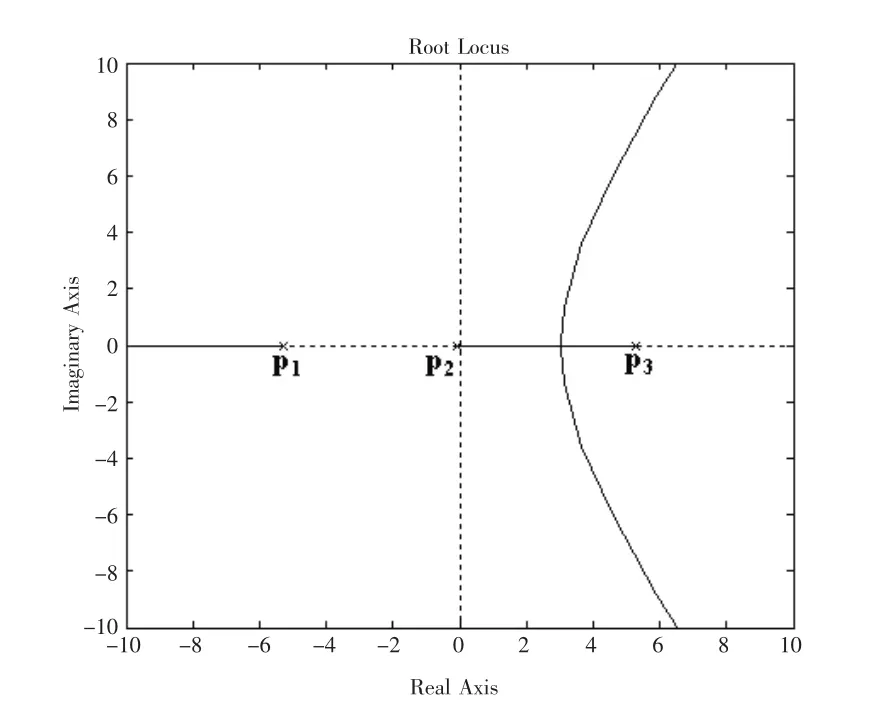
图4 消掉原点处零点后的根轨迹

第2步：基于主导极点的初步校正。为了使系统稳定，而且还要满足期望的性能指标，必须设法使右半平面的两条根轨迹“调头”转向左半平面，而且迫使它们的方位和形状有利于改善系统的稳定性和动态性能。根据根轨迹“起于开环极点，终止于开环零点”和“对称于实轴”的基本规律，应在左半平面“恰当地”添加两个开环零点z1和z2，问题的关键是如何确定z1和z2的具体位置。由于根轨迹的实质是系统闭环特征根在s平面上变化的轨迹，因此要确定两个零点，即“终点”的位置，必须首先研究根轨迹“路径”即特征根所应遵循的规律。

由于倒立摆是一个高阶系统，它应具有一对共轭主导极点，其位置对系统动态性能起决定性的影响，因此可把系统近似成二阶欠阻尼系统来处理，相应地可把对系统性能指标要求转化为对系统希望的主导极点位置的要求［5]。本文中对系统期望的性能指标为：超调量σ%＜1.5%，调节时间ts＜2s。图5展示了二阶欠阻尼系统闭环极点位置、结构参数与动态性能的关系。根据对性能指标超调量的要求 σ%＜1.5%，对应的阻尼比 ξ＞0.8，图中β＝arcosξ＝arcos0.8≈37°，则可确定期望的主导极点应位于图中β＜37°且β＞－37°虚线夹角的扇形区域内。对调节时间 ts＜2s，由 ts＝4／ξωn得 ξωn＝4／ts＝4／2＝2，可知希望的主导极点应在图中垂直虚线（小于－2）之左。现在要同时满足超调量和调节时间的指标，希望的极点应位于图5中黑线区域以内。

图5 确定主导极点范围的示意图

通过对闭环极点的位置与动态性能关系的进一步研究表明［5] ［6]：要提高系统的平稳性以减小响应超调，应使闭环极点靠近实轴；要提高系统的快速性，则闭环极点应远离虚轴；要求动态过程尽快结束，应该使闭环极点在容许的区域内远离原点。但闭环极点距离虚轴或原点也不宜过远，否则控制力会过大，在系统结构参数和硬件上会受到制约。综合上述的分析并根据实践经验，可以将“希望的主导极点范围”限制在图5中下列区域：①必须在黑线区域以内；②尽量靠近负实轴；③相对比较靠近－2垂直线。

参考上述主导极点的范围，确定两个零点的位置就比较有把握了。为使问题简化，取两个实数零点，初步将两个零点确定在负实轴上的z1＝－2和z2＝－3的位置，此时绘制的根轨迹如图6（a）所示，根轨迹的“形状”达到了预期的目的：使右半平面的两条根轨迹“调头”转向了左半平面，在负实轴上会合后，终止于这两个零点。

第3步：检验控制系统的性能指标。通过第1步和第2步，共添加了一个开环极点和两个开环零点，为了检验校正后控制系统的性能指标，根据图3的原理图，在Matlab环境下编写程序代码，构建倒立摆闭环控制系统，以单位脉冲信号来模拟干扰输入f，计算并观察闭环系统的单位脉冲响应输出y，程序中充分利用了Matlab提供的函数rlocfind［7]，它能使用户非常容易得到根轨迹上的极点对应的根轨迹增益K，使得程序设计非常简便。在图6（a）的根轨迹上，在其“希望的主导极点范围”段上选取了一对闭环极点-2.48+0.09i和-2.48-0.09i，并返回了增益值K＝85.5871来求取相应的闭环脉冲响应。此时摆杆角度的单位脉冲响应如图6（b）所示，可以看出系统的稳定性和超调量满足要求，但调节时间ts＞3s较长，系统性能还有进一步完善的空间。

图6 初步校正后系统根轨迹及脉冲响应

第4步：进一步完善的校正。根据前面的研究表明，为了缩短调节时间，应将主导点的位置向左做适当移动，这只需将两个开环零点的位置向左适当移动，经过进一步调整，最终将两个零点的位置确定为 z1＝-3 和 z2＝-4。此时的根轨迹如图 7（a），按照与前面同样的原则和方法，最终得到的单位脉冲响应图7（b）。系统的性能得到了提高，基本达到了预期的设计目标。通过上述探讨作出如下总结。

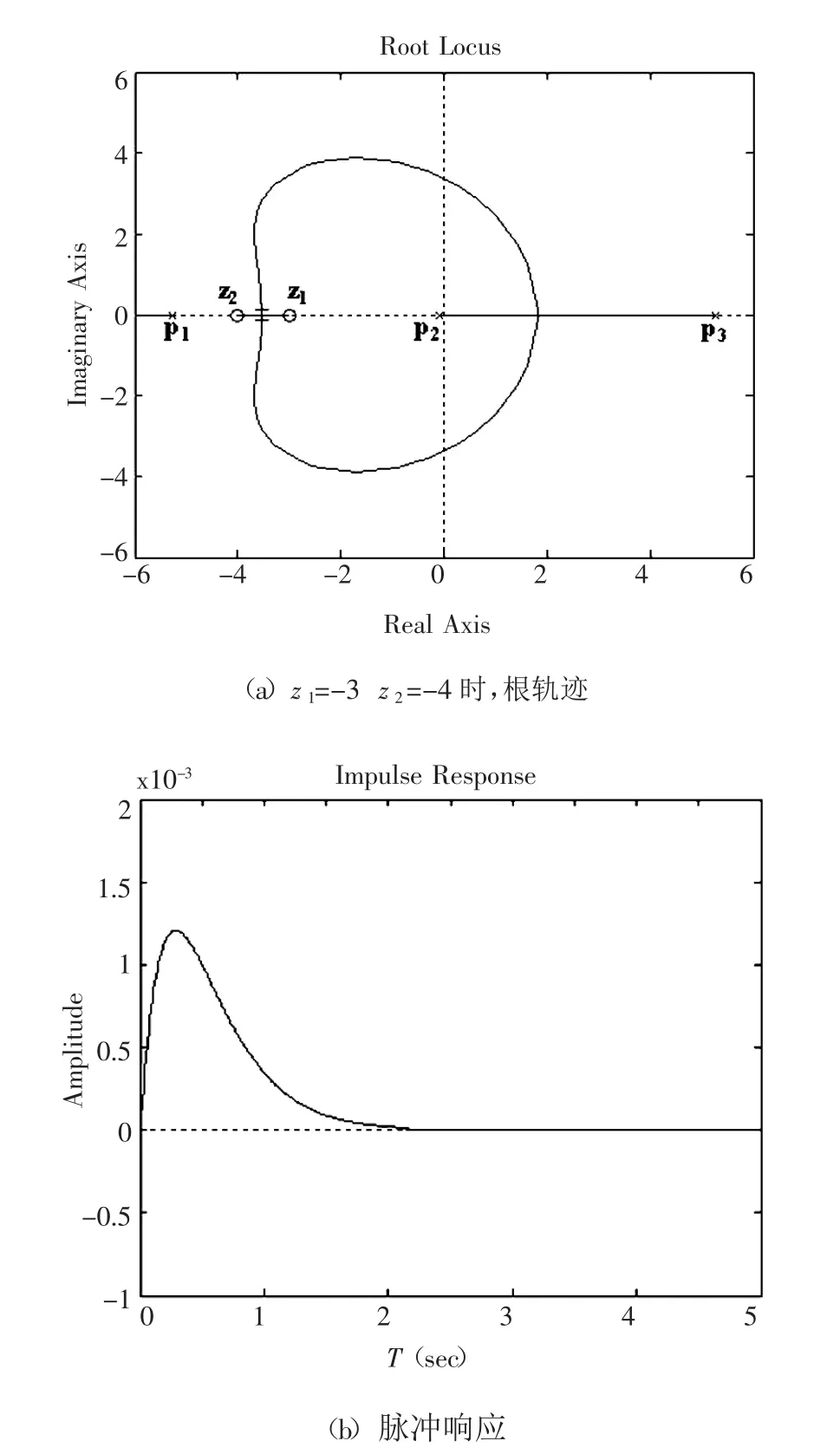
图7 最终校正后系统根轨迹及脉冲响应

实际的控制对象通常复杂多样，有时可不拘泥于固定的方式，需要具体问题具体分析，设计方法越简单快捷越好。因此在着手进行根轨迹校正之前，要对控制对象的零极点分布情况、根轨迹曲线的特点和对象的特性进行认真的研究和分析。

对于高阶或复杂系统的校正，通常不能一步到位，往往需要几个步骤才能完成。本文首先在原点处添加一个极点消掉那里的零点，可使得下一步的校正工作更为简化。

采用根轨迹校正法要遵循根轨迹的基本法则，灵活运用，不必抠得太死，面面俱到；开环零极点对根轨迹曲线的影响乃至对闭环系统性能的影响是根轨迹校正法的基础和灵魂。

本文的“主导极点法”是将高阶系统近似成二阶系统的处理方法，是一种很近似的工程设计方法，实际中要具体问题具体分析，灵活应用，不容易一步到位，往往还需根据实际情况进行反复校正。

4 结束语

本文针对倒立摆控制系统的设计问题，采用了一种根轨迹方法，完成了控制系统的设计，满足了预期的性能指标。它以达到性能指标为目的，以分析和改进根轨迹曲线为主要手段，无须常规方法的几何作图或数学解析，设计过程简单、直观、快捷，对于高阶控制系统的设计具有一定的参考价值。

［1] 黄忠霖.自动控制原理的MATLAB实现［M] .北京：国防工业出版社.2007.336－342.

［2] 张若青，罗学科，王 民.控制工程基础及MATLAB实践［M] .北京：高等教育出版社.2008.281－283.

［3] 杨世勇，谭 翚，刘殿通.倒立摆控制系统的设计与研究［J] .电气传动自动化，2011，33（2）：34－37.

［4] 杨世勇，徐莉苹，王培进.单级倒立摆的PID控制研究［J] .控制工程，2007，14（增刊）：23－24，53.

［5] 胡寿松.自动控制原理（上）［M] .北京：国防工业出版社.1984：324－328.

［6] 孙虎章.自动控制原理［M] .北京：中央广播电视大学出版社［M] .1994：89－112.

［7] 楼顺天，于卫.基于MATLAB的系统分析与设计—控制系统［M] .西安：西安电子科技大学出版社，1998：79－80.