基于AMSAA-OCM方法的鱼雷实航可靠性评估
马强 张志华 梁胜杰
(1.海军工程大学 应用数学系,武汉 430033;2. 海军工程大学 兵器工程系,武汉 430033)
0 引言
在鱼雷研制过程中,承制方需要进行大量试验,以验证鱼雷可靠性设计是否合理。根据鱼雷研制特点,鱼雷可靠性研制试验基本可分为组件陆上试验和全雷湖海试验。为保证鱼雷组件设计的合理性,在鱼雷研制前期,承制方将重点开展各类组件试验,以考核验证组件的可靠性。在组件可靠性得到验证后,承制方将以全雷湖海试验为主,综合验证鱼雷性能和可靠性。为了综合利用两类可靠性研制试验信息,本文提出了鱼雷实航可靠性的 AMSAA-OCM评估方法,提高了可靠性评估的精度。
1 鱼雷研制阶段可靠性增长模型
1.1 AMSAA模型
AMSAA[1]模型是指可修系统在开发期(0,t]内失效次数N(t)有均值函数γ(t)=E[N(t)]=αtb及瞬时强度λ(t)=dE[N(t)]/dt=abtb-1的非齐次 Poisson过程。可修系统开发到时刻T定型,之后对系统不再作改进或修正。系统的MTBF为

α>0为尺度参数,b>0为增长参数。当0<b<1时,λ(t)严格单调下降,系统可靠性增长。当b>1时,λ(t)严格单调上升,系统可靠性下降。当b=1时,λ(t)=α非齐次Poisson过程退化为Poisson过程,系统可靠性既不增长也不下降。
1.2 顺序约束模型
在鱼雷湖海试验中,暴露的故障需要在每次试验结束后进行集中修正,从而使鱼雷可靠性产生阶段性增长。因此,可以利用顺序约束模型[2]对全雷湖海试验数据进行处理,其各次试验的可靠度满足顺序约束条件:
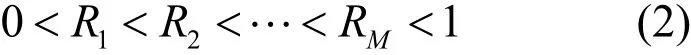
2 评估方法
2.1 组件陆上试验可靠性评估
组件可靠性数据通常为增长型数据,其数据结构为 0<t1≤t2…≤tn≤T,根据组件数据的特点,本文选用AMSAA模型评估组件可靠性。由此可知其似然函数[3]为

由统计学知识解得参数a、b及鱼雷在时刻T时的MTBF的无偏估计

给定置信度 1-a,鱼雷组件在时刻T时的MTBF置信下限为

其中π值可查国军标 GJB/z77《可靠性增长管理手册》得到。经过AMSAA增长模型评估后,就可以得到鱼雷组件在任务时间0t时刻的可靠度的点估计和可靠度置信下限分别为

2.2 组件陆上试验信息综合等效
1) 组件陆上试验等效数据
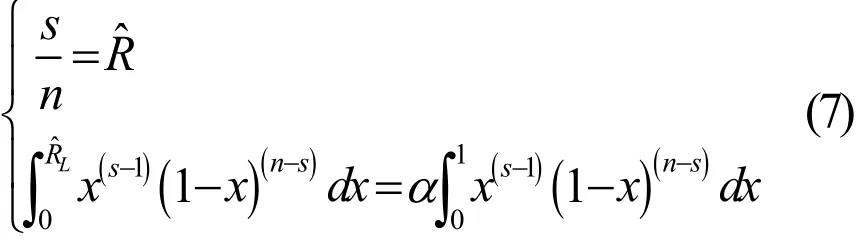
其中:(1-a)=0.8,n为等效总试验次数,s为等效总成功次数。设鱼雷共有K个组件串联组成,其中第i个组件的陆上试验等效数据为(ni,si)。由
长期高血糖引起机体蛋白质非酶糖化,形成的糖基化终产物(advanced glycation end product,AGE)大量堆积是导致视网膜毛细血管周细胞凋亡和 DR 发生的主要原因[10]。糖化血红蛋白含量与红细胞聚集速度呈正相关,大量红细胞聚集易使微小动脉形成血栓;糖化血红蛋白对氧的亲和力增大,氧解离速率降低,使组织缺氧,诱发多种血管生长因子表达增加,这是 DR 发生和进展的基础[11]。缺血、缺氧可导致光感受器和双极细胞层水肿和增厚,色素上皮层细胞水肿以及双极细胞排列紊乱[12]。
L-M方法可得到全雷的陆上试验等效数据为:

该综合方法实际上是设想鱼雷系统进行了N¹次试验,共出现S¹次成功,由于成功次数S¹不一定是整数,可用最接近它的整数代替或用插值法[4]处理。
2) 全雷湖海试验等效数据
为了更加客观地评估鱼雷实航可靠性,必须利用环境因子对全雷陆上试验等效数据进行折算。本文将该等效折算数据(N0,S0)作为第 0次全雷湖海试验数据
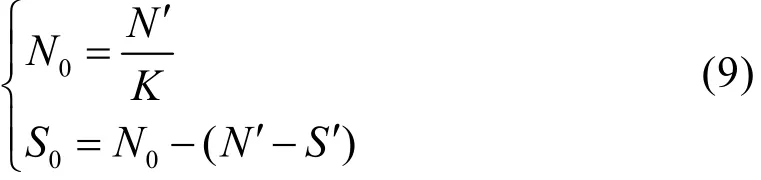
从而增加了全雷湖海试验信息,为提高实航可靠性评估精度奠定了基础。其中:K为环境因子,在鱼雷研制中通常取 2K= 。
2.3 鱼雷实航工作可靠性评估
设鱼雷到目前为止已进行了M次全雷湖海试验,加上第0次全雷湖海试验等效数据,共有M+1次全雷湖海试验数据,即:

记第j次全雷湖海试验时的鱼雷实航可靠度为Rj(j=0,1,2,…,M)。各次湖海试验的实航可靠度满足顺序约束条件:
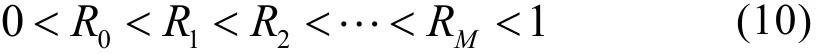
假设各次湖海试验结果相互独立,对于试验数 据 (Nj,Sj)(j=0,1,2,…,M) , 记rj=Nj-Sj(j=0,1,2,…,M),其似然函数为

M+1次湖海试验结果的似然函数为
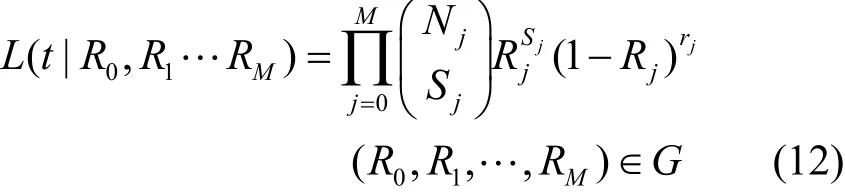
其中:G={(R0,R1,…,RM):0<R0<R1<R2<…<RM<1},t= {(Sj,rj),j=0,1,2,…,M}。由统计学知识,可得RM的后验分布g(RM|t).。再根据后验分布g(RM|t)就可得到第M次湖海试验结束时的鱼雷实航可靠度估计为:

给定置信度为1-a,第M次湖海试验结束时鱼雷实航可靠度RM的置信下限满足:

3 应用实例
设某鱼雷系统由K个组件串联组成,利用AMSAA-OCM方法评估其实航可靠性如下:
组件可靠性信息见表1。设组件1的任务时间t0=1h,组件2的任务时间t0=0.8 h,根据3.1节方法利用AMSAA模型对组件信息进行处理,得到组件1和组件2在置信度1-a=0.8下的模型参数和可靠性特征量的估计见表2。

表1 组件陆上可靠性试验信息表

表2 模型参数和可靠性特征量估计

表3 鱼雷湖海试验可靠性信息
=0 .8453。利用经典评估方法对鱼雷实航可靠性进行评估得= 0 .8333,= 0 .7147,= 0 .8700,= 0 .7358,与本文方法相比,由于没有考虑可靠性信息的增长特点,评估结果较为保守。若利用只考虑3次全雷湖海试验信息的可靠性增长方法进行评估,得= 0 .8701,= 0 .8063,= 0 .9194,= 0 .8621。由于每次全雷湖海试验量相对较小,而组件陆上可靠性试验信息较为充足(等效试验条次数为46,故障条次数为 12),本文方法对组件信息进行了充分利用,因此评估精度更为稳健可信。
4 总结
本文针对鱼雷研制阶段收集到的鱼雷组件陆上试验信息和全雷湖海试验信息,提出基于AMSAA-OCM 模型的鱼雷实航工作可靠性评估方法,有效的解决了组件陆上试验信息和全雷湖海试验信息的综合利用问题,提高了鱼雷实航可靠度的评估精度,为订购方的可靠性监督工作提供了有力的理论支撑,具有一定的工程借鉴意义。
[1]Crow L H. Estimation procedures for the Duane model[R]. ADA019372, 1972: 32-44.
[2]Smith A F M. A Bayes notes on reliability growth during a development testing program[J]. IEEE Trans.on Reliability, 1977, 26: 346-347.
[3]周源泉, 翁朝曦. 可靠性增长[M]. 北京: 北京科学出版社, 1992.
[4]关治, 陈景良. 数值计算方法[M]. 北京: 清华大学出版社, 2002.

