空间站组装过程姿态控制方案研究

李广兴，肖余之，卜劭华，颜根廷

（上海宇航系统工程研究所，上海201108）

1 引言

根据我国载人航天工程规划，我国计划发展空间站系统，解决有较大规模的、长期有人照料的空间应用问题。由于运载能力的限制，空间站一般由多个舱段在轨组装而成，舱段之间通过对接机构实现刚性连接。空间站组装的各个阶段，可以形成不同的构型，对控制系统的要求也不尽相同。

就实现组装过程的手段来说，一般有两种途径[1]。一种是利用大型机械臂系统，如国际空间站的遥控操作器系统（SSRMS）；另外一种是利用具有特定转位功能的系统，如“和平”号Mir空间站的再对接机械臂系统（即转位机构，RMS）。RMS具有结构设计和过程控制简单，自动控制程度和控制精度高、地面试验和设备复杂度低等优点，因此利用其实现组装过程是最经济有效的手段。

空间站从“一”字形变为“L”形等构型的组装过程中，需要把实验舱从轴向对接口转移到周边对接口，此时待转舱处于停控状态。如果待转舱的太阳电池阵系统具有收拢功能，那么可以把电池阵收拢，以避免对核心舱产生不必要的干扰。组装过程中，如由姿控发动机实现对组合体的控制，可能引起严重的控制/结构耦合问题，进而对结构造成破坏性的影响，因此只能用CMG进行组合体的姿态控制。

如果负载运动对核心舱产生常值干扰力矩，会造成CMG饱和，必须对角动量卸载才能恢复CMG的重新控制能力。为避免角动量饱和，一类方法是对核心舱的姿态进行优化处理，设计期望的姿态轨迹[2，3]，使CMG需要吸收的摄动角动量较小；另一类方法是对机械臂操作路径和运动特性进行规划，使得负载的运动对核心舱产生较小的扰动，CMG不易饱和。

组装过程的另外一个显著特点是空间站组合体的质量特性（质量和质心等）发生了较大变化，给控制系统的设计带来困难。利用RMS进行组装，系统动力学参数呈现慢变的特性，可采用自适应控制技术[4]或鲁棒控制技术对姿态控制进行设计。

本文针对空间站组装过程中可能出现的CMG饱和特点，设计了RMS的运动规律，避免使用姿控发动机对CMG角动量卸载。针对质量特性变化大的特点，设计了强鲁棒非线性PID控制律，从而有效的消除质量特性变化对控制系统带来的不利影响。

2 动力学模型

空间站组合体由核心舱和实验舱组成，RMS的旋转臂安装在实验舱上，在核心舱的节点舱安装RMS的旋转基座。图1为“一字形”构型示意图，图2为舱段转移过程示意图。

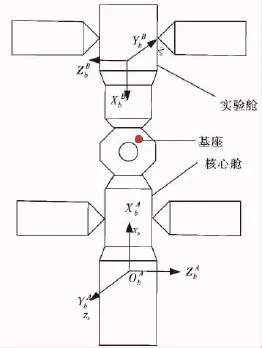
图1 “一字形”构型示意图

图2 舱段转移过程示意图

运动学方程为

I3×3表示单位矩阵。分析（1）式，可得空间站的控制力矩Tc为

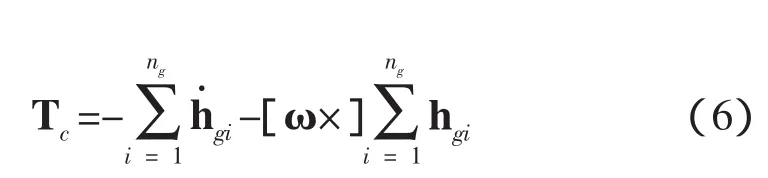
实验舱旋转产生的扰动力矩为

而Td中则包含了重力梯度力矩和气动力矩，即

其中，Tg为重力梯度力矩，Ta为气动力矩。

3 GNC系统组成

空间站系统组成部件包括：由陀螺组合和加速度计组合构成的惯性测量单元（IMU），光学姿态敏感器（包括红外地球敏感器、数字式太阳敏感器、模拟式太阳敏感器和0-1式太阳敏感器，星敏感器），GPS/GLONASS兼容接收机、磁强计和GNC控制器等。执行机构包括喷气发动机，控制力矩陀螺、太阳帆板驱动机构等。力矩陀螺构形和整个系统组成如图3、图4所示：

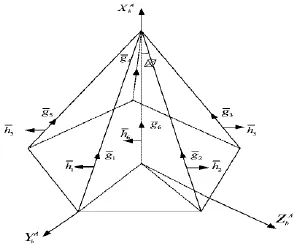
图3 力矩陀螺构形示意图

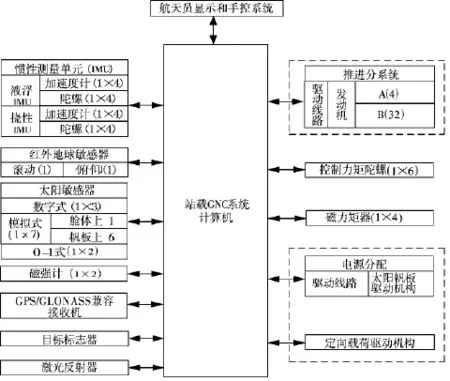
图4 GNC系统组成

各控制力矩陀螺框架角零位状态下，陀螺角动量垂直于框架轴且指向外，位于框架轴和轴所在的平面内。

4 RMS运动规律设计

核心舱前端的节点舱有多个对接口，但是很难在节点舱的周边对接口进行组装[1]，这是因为：①空间站上的一些突出机构（主要是太阳电池阵）妨碍了直接对接；②周边对接还需要其它辅助装置，如标靶、信号灯、雷达天线等；③从对接过程中空间站动态载荷的角度看，直接径向对接可能导致大角度失稳，影响空间站的姿态。因此，初始的对接通常都是从轴向开始的，然后利用舱段转移器，将舱段转移到周边对接口，实现再对接。由于RMS的转位过程只涉及旋转臂和待转舱体的翻转和摆动，运动方式单一，锁紧和解锁机构能适应一定的姿态偏差，可以降低空间站相对位置和姿态的控制难度。RMS由两部分组成，①旋转臂，装配到再对接舱上；②旋转基座，安装在核心舱上的节点舱上。RMS和旋转过程如图5和图6所示[5]。RMS通过三次旋转，可以实现负载的再对接，由几何原理可确定运动路径。

图5 舱段RMS的旋转臂与旋转基座

图6 RMS工作过程

定义两个坐标系，转臂旋转坐标系FM和基座旋转坐标系FS。由于FM固连于转臂，FM与之间的转换需经两次旋转完成。因为绕坐标轴Zm的翻转与绕坐标轴YS的摆动旋转特性相似，因此只需对FM中的运动规律进行设计即可。表1给出了指标约束，表2给出了实验舱的质量特性参数。

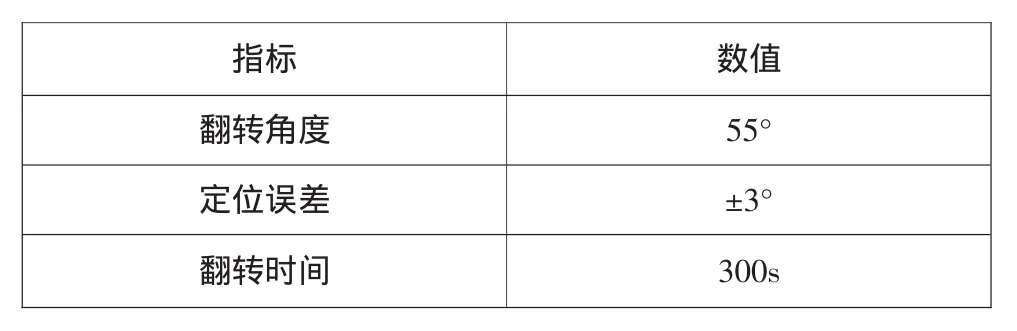
表1 指标要求

为避免控制力矩角动量饱和，必须使翻转过程中的角加速度尽量小。在满足约束条件下，需要设计两个的重要参数，即绕Zm轴翻转的角加速度εer和加速时间t1的量值。图7给出了设计的速度曲线，分为加速、匀速和减速过程。对核心舱的干扰主要体现在加速和减速过程，匀速过程比较小。对于减速段，尽管有50°左右的翻转角，但是干扰角动量与加速段相差不大，但方向相反，基本上会平衡掉加速段产生的扰动量。另外，还可以对加减速过程进行多段多级设计，减少翻转过程带来的干扰。

表2 实验舱质量特性参数

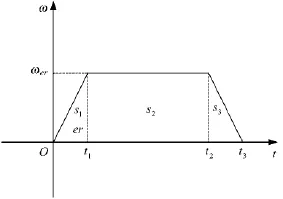
图7 翻转角速度曲线

根据图7，列写以下等式

并且满足约束条件

其中，s1，s2和s3为机械臂加速、匀速和减速的旋转角位移，t1，t2和t3为对应的时刻。在 FM中，ωer=［0 0 εer］T，‖·‖表示 2-范数。

计算式（9），并满足约束条件（10），得

5 姿态确定算法

组装过程中，空间站角速度较小，可以采用星敏和陀螺组合的姿态确定算法。

（1）陀螺的数学模型

为简便起见，假设陀螺测量系与核心舱本体坐标系重合。

陀螺数学模型如下：

其中ω表示本体坐标系下的角速度矢量，b表示陀螺偏差，其中v，n是不相关零均值高斯白噪声。

（2）星敏感器的数学模型

星敏感器的输出需要将向量量测转换为四元数信息，量测噪声也需要转换成四元素，即量测噪声nsc=［（ns）T1］T，得到的星敏感器输出四元数 qsc为

式中，q表示赤道惯性系到本体坐标系转动的真实姿态四元数信息，⊗表示四元素乘法。如果考虑星敏感器在舱体坐标系上的安装矩阵，可以通过坐标转换将星敏坐标系的姿态四元素输出转换到舱体坐标系。设将星敏坐标系到舱体坐标系的安装四元素为qsb，得到的星敏感器在舱体坐标系下的输出四元素为：

星敏感器的量测噪声ns可以认为是高斯白噪声。

定义如下姿态误差四元数

式中，qe表示姿态误差四元数表示地心赤道惯性系到本体坐标系转动的姿态四元数估计值，它等于飞行器的真实四元数q旋转一个小的误差四元数qe。

式中

设星敏感器测量坐标系与本体系重合，由星敏感器测量方程可推导出滤波的测量方程如下：

其中，qesc为星敏感器的测量四元素与估计的四元素之间的误差四元素。观测方程矩阵形式可以表示为：

其中，Z（t）=Qesc=（qesc1qesc2qesc3）T，H=［I3×303×3］，V（t）=vsc。对两方程离散化即可进行卡尔曼滤波进行姿态估计。

6 姿态控制算法

空间站组装过程中，质量特性变化剧烈。因此必须设计强鲁棒的控制算法，克服负载运动和环境带来的干扰力矩。

引入非线性函数fnl，定义如下：

式中，β为指数收敛系数，δ为切换开关系数，x为输入变量，sign（·）表示符号函数。其思想在于当误差超过设定的阀值时，控制输出为非线性指数形式，以增加控制量，当误差小于设定的阀值时，控制输出为线性形式，以减小控制量。令kPi、kli、kDi和为各个通道的比例、积分和微分系数，KP=diag（kP1，kP2，kP3），KD=diag（kD1，kD2，kD3），=[fnl1fnl2fnl3]T，则非线性PID控制律表达式为：

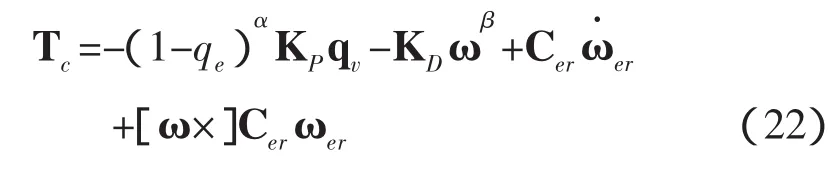
考虑到组装过程时间短，气动和重力梯度力矩引起的扰动角动量很小，有如下的定理：

定理：对于（1），（2）和（3）描述的空间站动力学模型，如果设计控制律如式（22），式（1）～（3）和式（22）中的所有信号有界，那么对于所有的物理可实现的初始条件，在控制律的作用下，闭环系统全局渐进稳定，并且有

证明：如果对机械臂的运动特性进行规划，ωer很小，（2）式和（3）式可以合成为

其中，η=diag（ηci，ηei），D=diag（Dci，Dei），K=diag（Kci，Ke）i=diag（，）。选择Lyapunov候选函数为

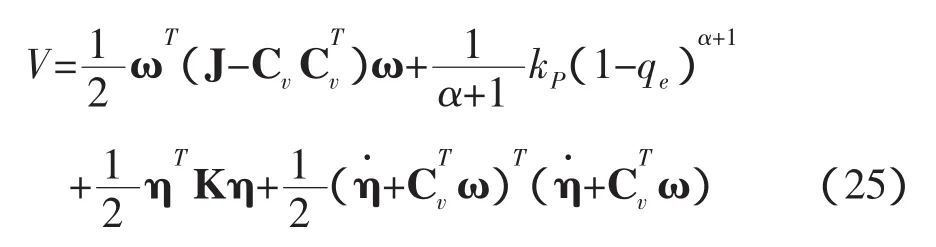
显然，V为正定函数，对V求导，得

经过简单的数学运算，式（26）变为

把式（22）代入上式，得

若β为偶数，则有

当且仅当ω=0，=0 时˙=0。把 ω=0，=0 带入误差动力学方程，挠性振动方程和控制律中，得到qv=0，η=0，进而有q0=1，因此由LaSalle全局不变集原理可知，控制算法能够保证闭环系统全局渐进稳定。如果，同样可以证明闭环系统也是全局渐进稳定的。

引入积分信号，最终产生鲁棒非线性PID 控制律为：

7 数学仿真

初始条件如下：

核心舱转动惯量

二象限帆板耦合矩阵

四象限帆板耦合矩阵：

挠性振动频率阵：

控制律参数：α＝-0.2，β＝［1 0.8 0.8］，

控制力矩范围：［-200 200］（Nm）

控制过程中，空间站组合体保持对地定向姿态，仿真结果如图8～13所示。

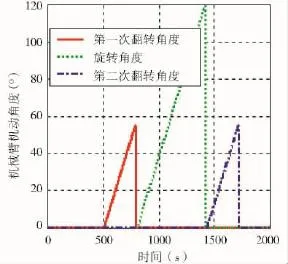
图8 期望翻转角度

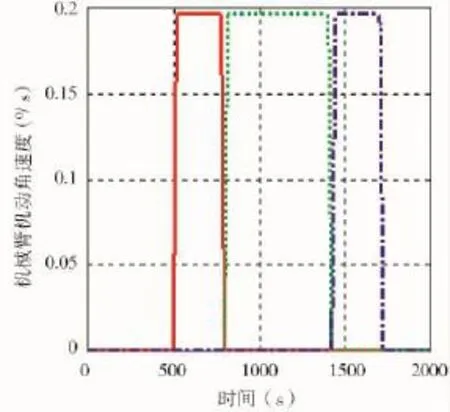
图9 期望翻转角速度

图10 非线性控制下的姿态角

图11 控制力矩

图12 力矩陀螺角动量

仿真结果表明，通过对再对接机械臂的翻转运动规律进行设计，不会引起控制力矩陀螺角动量饱和，避免使用姿控发动机进行卸载。图10和图13为同一初始条件下，非线性与线性控制下的姿态角曲线，结果表明本文所提出的非线性PID律具有更好的控制性能。

图13 线性控制下姿态角

8 结论

本文对空间站组装过程中的控制方案进行了研究，对再对接机械臂翻转过程中的运动规律和鲁棒姿态控制律进行了设计，对敏感器组成、力矩陀螺构形和姿态确定方案进行了初步的探讨。解决了可能出现的控制力矩陀螺角动量饱和问题。采用非线性PID控制律，增加了控制系统的抗干扰和适应性能力。 ◇

［1］朱仁璋，王鸿芳，泉浩芳，等.载人航天器操作系统评述［J］.载人航天，2010，16（1），48-58.

［2］马艳红，张军，郭廷荣.空间站组装时的姿态指令优化［J］.载人航天，2010，16（1），17-20.

［3］Mapper，J.，Tsay-Hsin G.Hu.Moment management controller design for space station during payload maneuver.AIAA-95-3310-CP，1995.

［4］S.J.Paynter.Adaptive Nonlinear Attitude Control of the Space Station.AIAA 94-0014，32nd Aerospace Sciences Meeting&Exhibit，January 10-13，1994.

［5］秦文波，陈萌，张崇峰，等.空间站大型机构研究综述［J］.上海航天，2010，27（4），32-42.