载人登月轨道设计方法及其约束条件概述
郑爱武 ,周建平
(1.北京航天飞行控制中心航天飞行动力学技术重点实验室,北京100094;
2.中国载人航天工程办公室,北京100720;3.北京航空航天大学宇航学院,北京100083)
1 引言
月球独特的空间位置、极具潜力的科学探索前景和丰富的可利用资源,决定了月球探测活动是当今世界航天领域中极具挑战性和显示度的领域之一。上个世纪50年代末以来,以美国和前苏联为首的世界航天大国开展了大量月球探测活动,取得了一系列成果,并带动了相关领域科技与应用的快速发展。在1959年到1976年的第一次探月高潮中,美国成功实施了6次载人登月,前苏联成功实施了2次无人月面自动巡视探测和3次无人采样返回任务。20世纪90年代开始,美国、俄罗斯、印度、日本和欧空局等主要航天国家和组织纷纷提出了新的月球与深空探测计划。美国登月的侧重点是资源方面,最终目的是火星,所以把月球当成中间站;欧洲的侧重点是技术,正在研究探月和登月的新方法和新技术;印度和日本的侧重点则是关于月球科学的研究。
在月球探测任务中,轨道的设计问题是所面临的一个最基本的问题,其设计的优劣直接影响任务执行的效果、甚至成败。近年来国内在载人登月轨道设计方面已取得了一些进展。刘兴隆基于圆锥曲线拼接法,从几何与力学角度对自由返回轨道进行了分析[1]。白玉铸等人应用分段受摄的高精度动力学模型,设计了搜索变量、约束条件与微分修正搜索算法,搜索得到了自由返回轨道和混合轨道[2]。黄文德等人给出了基于双二体假设的轨道初步设计,对自由返回轨道的飞行时间、轨道倾角、近月距和轨道拼接点分布等参数进行特性分析[3],并在双二体假设的基础上,考虑月球运动的非圆性,给出了混合轨道的设计实例,对混合轨道的特性进行了分析[4]。黄文德、陈海萍和郗晓宁等人还针对混合轨道的中止需求,在双二体的假设下,建立了直接中止、多脉冲中止和借助自由返回轨道中止等三种中止方式的轨道计算模型。并分析了任务中止方式、中止轨道在能量需求和返回飞行时间等方面的特性[5-6]。
国外载人登月各个阶段积累的成功经验和失败教训,可以为我国实施载人登月计划提供思路和启发。本文总结了国内外载人登月轨道设计的方法以及相关的研究成果,重点概述了载人登月的轨道类型、设计方法、约束条件、优化原则和飞行模式。
2 载人登月的轨道类型
根据Apollo载人登月的成功经验,为保证航天员的安全,用于载人登月的轨道主要有两种类型:自由返回轨道和混合(Hybrid)轨道。自由返回轨道已被美国应用在Apollo 8,10,11任务中,从Apollo 12开始的后续任务,包括Apollo 13在内,采用的是混合轨道[7-8]。
2.1 自由返回轨道
自由返回轨道是载人登月任务首选的一类转移轨道,也是载人登月轨道设计的基础。如图1所示,载人飞船只在地月转移轨道入轨点(TLI)进行一次变轨,其后不加机动或略加修正,飞抵近月点后在引力作用下绕过月球并自动返回地球附近。Apollo首选的自由返回轨道是一条近月点高度大约为60海里(111km)的轨道。
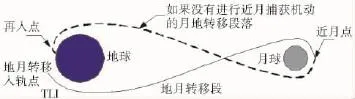
图1 自由返回轨道示意图
自由返回轨道的安全性高,如果航天员或飞船出现意外无法完成登月任务,那么这种轨道可以在不实施近月点制动情况下使飞船自动沿预先设计的轨道返回地球,从而挽救航天员的生命。但自由返回轨道的倾角有限,相对月球赤道面的倾角在大约10°以内,因此着陆点也限制在月球赤道附近。
2.2 混合轨道
混合轨道由自由返回轨道与非自由返回轨道组合而成,如图2所示。

图2 混合轨道示意图
混合轨道在实施TLI后先进入一条自由返回轨道,该轨道的近月点高度有可能很高,从60海里(111km)到几千海里。大约在TLI后一天(通常在半途之前),航天器进行一次机动,进入一条近月点高度大约为60海里的转移轨道,理论上该轨道不再是自由返回的。在Apollo计划中根据预期的误差传播,该轨道可以通过机动修正为自由返回模式,但修正的时机有限,一旦进入月球影响球,仅通过服务舱反应控制系统(SMRCS,推力很小,通常只用来进行中途修正[9])完成不了轨道修正任务,此时可利用登月舱下降推力系统(LM DPS)替代SMRCS进行修正。因此,混合轨道设计还需要综合考虑任务中止轨道设计的要求。
由于混合轨道月球轨道入轨(LOI)所需的燃料比自由返回轨道少,因此可达月球的范围更宽。通常,混合轨道可达到的倾角从大约0°~15°(低能量)或者0°~30°(高能量)。Apollo计划中,实施登月的Apollo 11-Apollo 17(除去未成功登月的Apollo 13)对月表的探测范围都在南北纬30°之间。
在以下情况下将选择混合模式而不是自由返回模式:
(1)当自由返回模式需要过多的燃料时;
(2)当自由返回模式到达月球的时间与一些限制条件发生冲突时(例如月球光照条件或特定地面站的覆盖范围)。
2.3 任务中止轨道
任务中止轨道不属于正常的轨道类型,而是为了保障航天员的安全,必须考虑在飞行过程中任一点出现故障时,都能使航天员安全返回地球的应急轨道。自由返回轨道具有很高的安全性,混合轨道除了自由返回轨道段具有自主返回的能力外,其它飞行段不具备自主返回的能力,因此,在设计时,必须同时考虑任务中止轨道的设计。实践表明,“阿波罗”计划的顺利实施与前期进行的任务中止轨道研究密不可分。在Apollo 13任务中,飞船在氧气罐爆炸后不能使用服务舱推进系统的情况下成功返回了地球[10]。
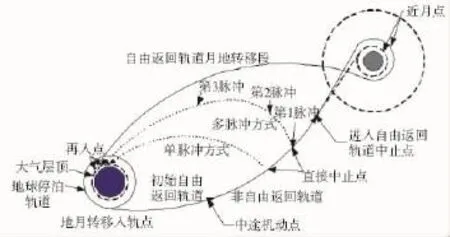
图3 混合轨道中止方式
如果故障发生在混合轨道的非自由返回轨道段,一般可以有两类中止方式:一类是借助自由返回轨道返回,飞船经历一次绕月飞行后返回地球;另一类是直接进入返回地球的轨道,也就是直接中止方式。直接中止方式中,根据变轨的方法,又可分为单脉冲方式和多脉冲方式。两种中止返回方式如图4、图5所示。
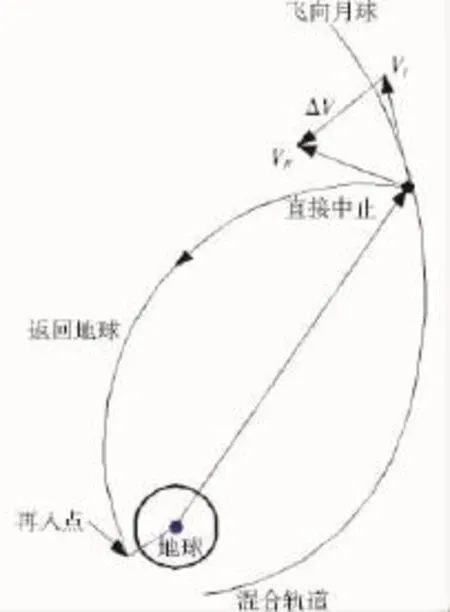
图4 单脉冲直接中止方式
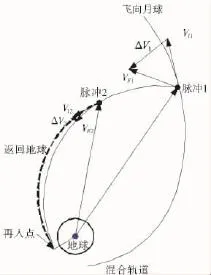
图5 双脉冲直接中止方式
自由返回轨道是在推进系统失效的情况下飞船能安全返回的最优轨道。对于给定中止点,设计中止自由返回轨道的方法与正常飞行的条件下自由返回轨道的设计并无本质区别,这里不再赘述。
在混合轨道的不同点位上,实现直接中止所需的能量不同。由于飞船所能提供的能量有限,在某些区域内,实现单脉冲返回是不可能的[11]。而有些区域,具有充足的能量用于返回,即能量过剩。因此,需要通过能量的优化,对于不能实现单脉冲中止的区域,利用多脉冲实现中止返回;对于能量过剩的区域,一方面,可以通过利用过剩的能量获取高能返回轨道,减少返回时间;另一方面,可以利用过剩的能量对返回轨道进行修正,使返回轨道末端处于再入走廊(由飞行航迹角决定)的中心地带,提高返回精度和安全系数。
3 载人登月轨道设计方法
在过去几十年的人类探测月球的活动中,各国的研究人员研究、发展出了多种转移轨道的设计技术,如脉冲转移方式、连续推力转移方式和基于弱稳定边界(WSB)的转移方式。不同转移方式需消耗能量的多少和转移时间的长短大不相同。
上世纪60~80年代期间所有的月球探测任务几乎都采用了经典的基于Hohman转移的直接转移方式,比如Luna和Apollo任务。典型的直接转移通常需要2d~5d。航天器应选择在当月球赤纬小于停泊轨道倾角(通常等于发射场的纬度)的时候发射[12]。九十年代提出了“返回月球”计划后,在轨道设计上有了更多的变化,采用了一些新的转移轨道设计方法来降低ΔV的需求[13-14]。例如,日本的“飞天”号(Hiten)任务同时使用了月球借力飞行(swing-by)和WSB的轨道设计方法捕获并进入大椭圆月球轨道。转移时间为6个月[15]。低能轨道在对时间要求不高的无人采样返回任务中具有广阔的应用前景[16]。
新的低能轨道设计方法可以大大节约燃料,如Ballistic转移比常规的Hohmann转移大约节省15%能量[17]。而且随着目前一些新的进展也使得飞行时间由原来的100d缩短到了13d~15d之间[18]。但对于载人登月来说,低能轨道的飞行时间还是太长,因此载人飞船的轨道设计方法还只能采用直接转移方式。不过,未来的月球基地建设中,货运飞船的轨道设计可以考虑更省燃料的低能轨道。
载人登月轨道设计的基本方法还是先采用简化的动力学模型快速获得轨道初始解,作为后续高精度轨道设计的初值,计算中采用相应的优化算法和搜索算法。直接转移初步设计方法有Hohmann转移、双椭圆转移、椭圆-双抛物线转移以及拼接圆锥法。这里主要介绍最常用的Hohmann转移和拼接圆锥法。
3.1 Hohmann转移
1925年Walter Hohmann得到了在限制性二体问题下,两条圆轨道之间最优转移轨道的一个解析解,该解被称为Hohmann转移轨道,它可以实现探测器在两个共面圆轨道之间最小能量的转移(R2/R1<11.94时,R1、R2分别为两圆轨道的半径)。如果将月球的公转轨道近似为圆轨道,也不考虑航天器如何被月球捕获的问题,那么,对从地球圆轨道出发的航天器而言,Hohmann转移是一种最便利的转移方式。
图6给出了利用Hohmann转移实现地月转移的基本过程(这里设地球停泊轨道的半径为R1,月球停泊轨道的半径为R2),其主要步骤为:
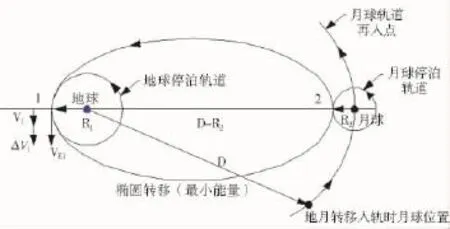
图6 地心系下Hohmann最小能量地月转移轨道
(1)第一步与普通的Hohmann转移相同,就是航天器在地球停泊圆轨道上运行到“1”处时施加第一个速度脉冲ΔV1,将轨道变为绕地球的椭圆轨道,其近地点就是“1”,其远地点位置在月球轨道附近。
由图6可以得到转移椭圆的半长轴amin:
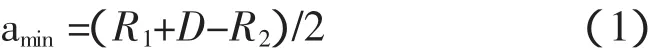
其中R1也是转移椭圆轨道的近地点地心距 ,V1是地球停泊圆轨道上的速度,VE1是近地点的速度,VE2是远地点的速度,D=384400 km是地月距,可以看作常数。
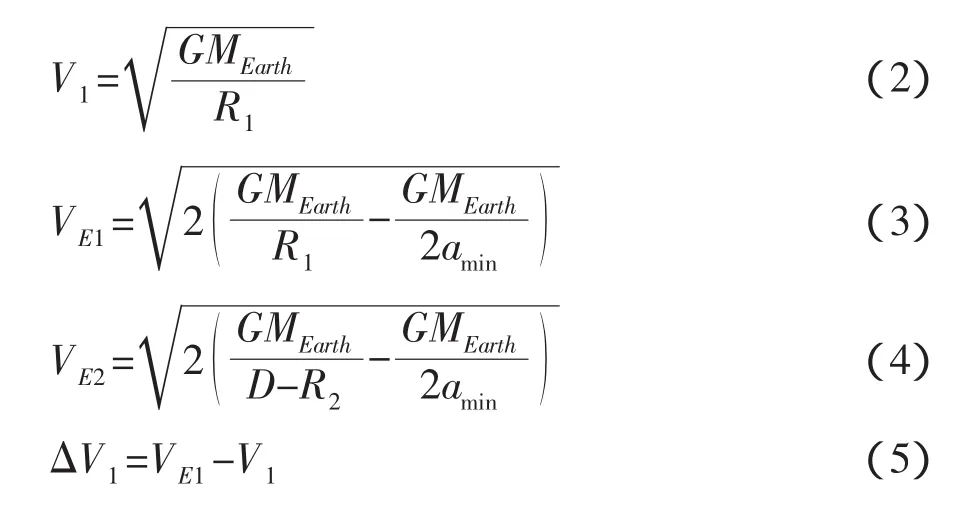
(2)第二步与普通的Hohmann转移不相同,因为第二次脉冲不是为了使航天器进入半径为D-R2的圆轨道而是进入月球停泊轨道,因此在转移轨道的远地点“2”处施加的第二个速度脉冲ΔV2与航天器的运动方向相反,如图7所示。
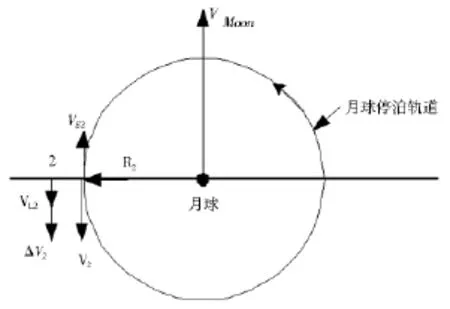
图7 Hohmann最小能量地月转移轨道月球段
这次制动航天器进入半径为R2的绕月圆轨道。VL2是远地点的速度相对月球的速度:
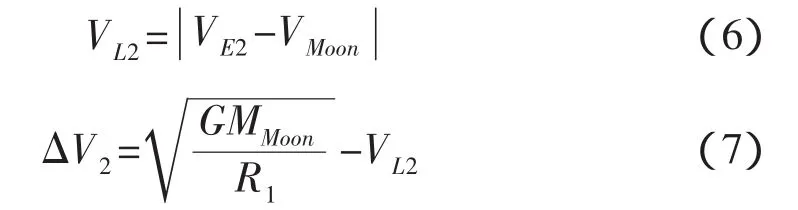
其中VMoon是月球绕地球公转的轨道速度,MMoon为月球质量。
由于Hohmann转移过程是在二体问题的基础上进行的,且将月球绕地球的公转轨道也看作圆,其所给出的转移轨道和所需的速度增量与实际情况相差较大,因此,Hohmann转移常被用于地月转移轨道设计的最初阶段,作为下一阶段设计的初始值。
3.2 拼接圆锥曲线
拼接圆锥曲线方法是地月转移轨道设计中经常采用的方法,计算结果的精度比Hohmann转移高,因此可以为后续的高精度轨道设计提供更好的初值,有利于搜索算法收敛。拼接圆锥曲线法引入了月球影响球的概念,它将地月转移轨道分成两段,如图8所示:地心轨道段与月心轨道段,这两段轨道在影响球边界上经适当拼接后形成满足要求的飞行轨道[19]。
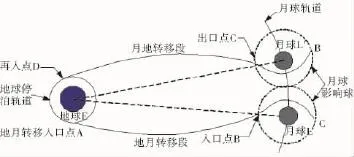
图8 轨道拼接示意图
图中B点为地月转移轨道与月球影响球的交点(即入口点),C点为航天器飞出月球影响球时与影响球的交点(即出口点)。L为入口点时刻月球的位置,L′为出口点时刻的月球位置,E为地球。AB和CD段为地心圆锥曲线,即忽略月球的影响,理论上地心段圆锥可以是椭圆、抛物线或双曲线。但椭圆所需要的速度增量最小。BC段在月球引力场内,此时忽略地球的影响,将航天器轨道看作绕月球的Kepler轨道(一般为双曲线轨道)。
当给定六个独立的轨道参数:地月转移轨道的近地距、加速点航迹角、入口点B的经、纬度、月心轨道倾角以及航天器在入口点处月心速度矢量与位置矢量反方向夹角时,可以利用解析公式求出地心轨道转移初速、加速点地心位置矢量、入口点B的地心位置和速度矢量、入口点B的月心位置和速度矢量。由入口点B的月心位置和速度矢量,可以求得出口点C的月心位置和速度矢量。然后通过坐标转换得到出口点C的地心位置和速度矢量。再由地心位置和速度矢量求出月地转移轨道段在地心坐标系中的倾角和近地距。
拼接圆锥曲线方法也是基于二体问题完成的,它在最初的轨道设计中是一种很好的近似,与精确轨道设计相比,除了对轨道力模型进行了简化(未考虑摄动力的影响)之外,两者在其它方面都是一致的。在双二体假设下得到的轨道,可以作为精确设计的初值,提高设计效率。不过,由于太阳引力场的干扰,以及第一段中月球引力场和第二段中地球引力场的干扰,这种近似在月球影响球部分是有显著误差的[19]。
3.3 高精度轨道设计
前述方法都是解析法,对轨道模型进行了简化,也没有考虑摄动项的影响。事实上,在地月系统的轨道设计中,摄动项的影响是非常大的。高玉东以双二体假设下得到的一条月地转移轨道为标称轨道,分析了摄动因素对轨道计算精度的影响程度,如表1所示[20]。
因此,虽然解析法的计算速度快,但精度不高,都只能作为高精度轨道设计的初值。高精度轨道设计还是需要基于高精度的轨道模型采用数值法积分。在开始轨道设计之前,需要综合考虑轨道设计的各种约束条件,寻求各种约束条件的平衡。
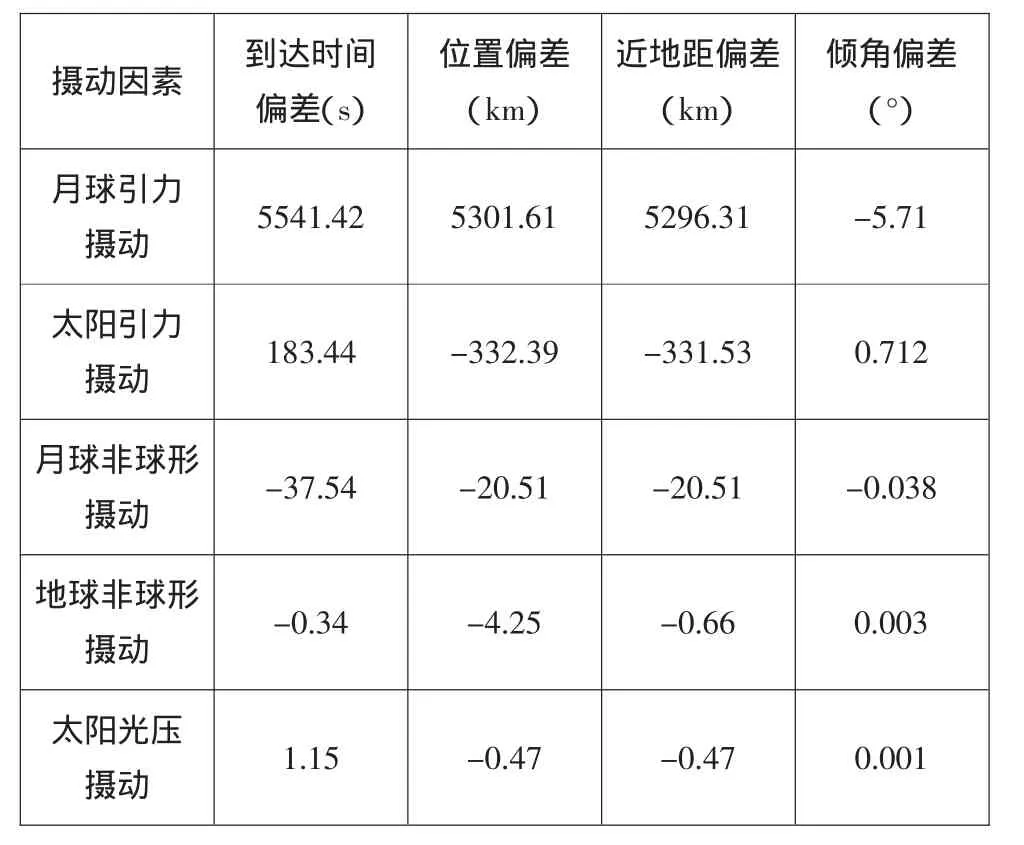
表1 各项摄动因素对月地转移轨道近地点时刻参数的影响
3.3.1 载人登月轨道设计的约束条件
参考Apollo11任务,在正常的载人登月轨道设计中需要考虑的约束条件包括[7]:运载火箭运载能力、发射窗口要求、发射场经纬度及发射方位角限制、入轨精度要求、航天器燃料量和航天器的推力系统和推力大小、月球着陆点的选择、月球着陆时的光照角要求、地球着陆时的光照角要求、测控覆盖范围、航天器轨道寿命或最长运行时间、航天器发热极限、航天器能否过月夜的能力、航天器过载限制、最大再入速度和再入走廊、着陆场选择、落点精度要求和飞行时间等等。如果航天器由使用运载火箭直接送入地月转移轨道,则发射方案和运载火箭决定了转移轨道的近地点高度和转移轨道倾角。
任务中止轨道设计也受到多方面的约束,包括:再入走廊、可使用的速度增量大小、返回时间、着陆区域、发射窗口、返回着陆时刻等[21]。再入走廊约束是任务中止轨道设计的最基本约束,无论以什么方式返回都必须满足。速度增量约束和返回时间约束是最主要的约束。如当飞船的推力系统出现故障时,可利用的速度增量有限,以最小速度增量返回就是最主要的目标。而当飞船上的生保用品不足或设备故障可能危及到航天员生命时,以最少时间返回又成了最重要的要求。这两个约束是相互矛盾的。当用最小速度增量返回时,所耗费的时间必然就长,而考虑最少时间返回时,所需要的速度增量也最大。通常要将最小速度增量和最少时间进行折衷,使任务中止轨道达到最优性能。如果在某个时刻进行任务中止的最小速度增量仍然超过了飞船现存推力系统的能力,那么在这个时刻就不能进行任务中止机动。这样就存在一个任务中止的可行性区间的问题。在可行区间内,可以直接进行任务中止,否则就必须等飞船进入可行区间后才能进行任务中止。
3.3.2 高精度动力学模型
通常情况下,在地月空间内运动的航天器受力包括:地心引力与月心引力、地球与月球非球形摄动、其他天体引力摄动、太阳光压摄动、大气阻力摄动以及地球潮汐摄动等。目前地月间最常用的动力学模型还是根据月球影响球进行分段的受摄二体模型。
根据Laplace的建议,以月球为中心的影响球半径为:
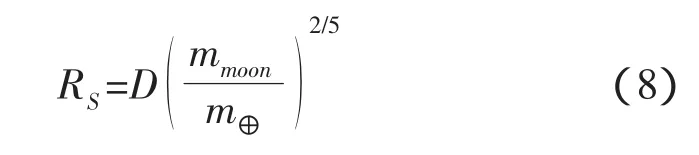
其中D为地月距,mmoon为月球质量,m⊕为地球质量。
分段受摄高精度动力学模型分为地心段和月心段:
地心段考虑地心引力、地球非球形摄动、日月引力摄动、太阳光压摄动与大气阻力摄动,月球和太阳的星历采用DE405,在理想惯性坐标系下的动力学方程如下:

其中,μe、μm和μs分别是地球、月球和太阳的引力常数和→分别为月球、太阳和航天器相对于地心的矢径,和分别表示航天器到月球和太阳的矢径为地球非球形摄动,为太阳光压摄动为大气阻尼摄动,相应的计算公式可参见文献[22]。
月心段(月球影响球内)考虑月心引力、月球非球形摄动、日地引力摄动与太阳光压摄动,动力学方程如下:

3.3.3 轨道优化原则
经典轨道设计的优化条件一般都是燃料最省原则。为了使所需能量最省,即总速度增量的模最小,需要对轨道设计过程进行优化处理。比如在自由返回轨道设计中,可以结合近月距和对月倾角等约束条件,取目标函数为:
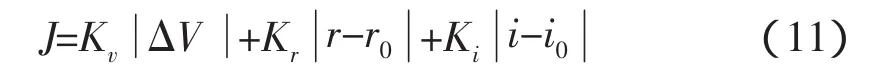
其中,r、r0分别表示实际近月距和要求达到的近月距,i、i0分别表示实际相对月球的轨道倾角和要求达到的轨道倾角。Kv、Kr和Ki为常数系数,分别用于调整三者之间的权重。于是,可以建立满足约束条件的最优化问题,应用最优化方法进行求解,得到满足约束条件的轨道。
一旦航天器发射升空,确保任务成功就是远比节省燃料更重要的问题了,特别是在任务发生故障或进入应急的情况下,因此轨道设计的优化条件也需要进行调整。在故障和应急情况下以燃料最省为原则没有意义。机动后没有使用的燃料最终也会被抛弃或返回地球。所以,在故障和应急情况下,主要是将可用的燃料作为一个限制条件而不是优化条件,对使任务更有风险的其他参数进行优化,比如返回时间,机动次数,或再入速度[23]。总而言之,主要目标是减少机动次数,其次是使飞行时间最短。
3.3.4 载人登月的飞行模式
载人登月的轨道设计还与载人登月的飞行模式紧密相关。优化载人登月的飞行模式,可以合理规划登月模块数量、规模和总体方案,明确火箭运载能力需求、发射次数,降低载人登月工程的研发难度,缩短研制周期,提高载人登月大系统工程的可靠性,节省研制经费。Apollo采用了单次发射(人货混运)+月球轨道交会(Lunar Orbit Rendezvous,LOR)返回登月模式,星座计划选用两次发射(人货分离)地球轨道交会(Earth Orbit Rendezvous,EOR)+LOR 返回登月模式,欧洲提出了四次发射,3次EOR+LOR返回登月模式。由于缺少超重型运载火箭,俄罗斯能源公司载人登月方案采取运载火箭7次发射,EOR(5次),+1次LOR返回登月的飞行模式[24]。盛英华等人基于载人登月飞行模式、飞行模块质量、可靠性和研制难度的分析,初步研究认为两次发射EOR+LOR返回登月模式是我国载人登月工程的较佳路线,但目前运载能力无法满足需求[25]。因此,较好的方案是三次发射(人货分离),两次EOR+LOR返回登月模式。
4 结束语
总的来说,国内关于载人登月轨道设计考虑的约束条件都还比较简单,比如仅考虑了近月点高度和环月轨道倾角,对月面着陆点位置、发射窗口、轨道两端的光照条件和地面测控等约束条件还需要进一步进行研究。
载人登月工程是一项技术含量高、复杂度大的大科学工程,具有极高的风险性。国外载人登月研究和实践积累的成功经验和失败教训,值得我们跟踪和研究,为我国实施载人登月计划提供思路和启发。本文总结了国内外载人登月轨道设计的方法以及相关的研究成果,详细介绍了载人登月自由返回轨道、混合轨道和任务中止轨道等三种类型轨道设计的设计思想、约束条件和优化原则。希望本文的工作能为我国未来的载人登月工程的任务轨道设计以及任务中止轨道设计工作提供参考。 ◇
[1]LIU Xinglong,DUN Guangren.Designs of optimal free-return orbit for moon landing [C].2007 IEEE Intematioual Conference on Robotics and Biomimetics(ROBIO),Sanya,2007:936-940.
[2]白玉铸,陈小前,李京浩.载人登月自由返回轨道与Hybrid轨道设计方法[J].国防科技大学学报,2010,32(2),:33-39.
[3]黄文德,郗晓宁,王威,李静.基于双二体假设的载人登月自由返回轨道特性分析及设计[J].宇航学报,2010,31(5):1297-1303.
[4]黄文德,郗晓宁,王威.基于双二体假设的载人登月混合轨道特性分析及设计[J].国防科技大学学报,2010,32(4),61-67.
[5]黄文德,郗晓宁,王威.基于双二体假设的载人登月中止轨道特性分析[J].宇航学报 2010,31(9):2067-2074.
[6]陈海萍.载人登月任务中止轨道特性分析[D].长沙:国防科技大学,2009.
[7]Ronald L.Berry.Launch Window And Translunar,Lunar Orbit,and Transearth Trajectory Planning and Control for the Apollo 11 Lunar Landing Mission.AIAA No.70-24,AIAA 8th Aerospace Science Meeting,New York,January 19-21,1970.
[8]Adamo D R.Apollo 13 Trajectory Reconstruction via State Transition Matrices [J].Journal of Guidance,Control,and Dynamics.2008,31(6):1772-1781.
[9]Anselmo D R,Baker M K.Translunar and Lunar Orbit Abort Trajectories for Apollo 14.NASA-CR-116280[R],Bellcomm,Inc.,Dec 7,1970.
[10]Richard W O.Apollo by the Numbers:A Statistical Reference[R].NASA SP-2000-4029,2000.
[11]Beksinski E D.Abort Trajectories for Manned Lunar Mission[D].University of Maryland,2007.
[12]R.Biesbroek,G.Janin.Ways To The Moon.ESA bulletin 103,august 2000.
[13]V.Krish,E.A.Belbruno,andW.M.Hollister,An investigation into critical aspects of a new form of low energy lunar transfer,the Belbruno-Millertrajectories.AIAA/AAS Astrodynamics Conference (South Carolina, 1990), American Institute of Aeronautics and Astronautics,Washington,DC,AIAA-1992-4581,1992:435–444.
[14]Koon W.S.,Lo M.W.,Marsden J.E.,et al.Low Energy Transfer to the Moon.Celestial Mechanics and Dynamical Astronomy,Kluwer Academic Publishers,Netherlands,Vol.81,2001:63-73.
[15]E.A.Belbruno and J.Miller.A ballistic lunar capture trajectory for the Japanese spacecraft hiten.Technical Report IOM 312/90.4-1731-EAB,Jet Propulsion Laboratory,Cal.Tech.,1990.
[16] Lo, M.W., Chung, M.J., Lunar Sample Return via the Interplanetary Superhighway.AIAA/AAS Astrodynamics Specialist Conference,Monterey,California,Paper AIAA 2002-4718,August 2002.
[17]T.H.Sweetser.An Estimate of the Global Minimum Needed for Earth-Moon Transfer.in J.K.Soldner, A.K.Misra, 1...1..Sackett,and R.Holdaway (eds.),Spaceflight Mechanics 1991,Volume 75,Part I of Advances in the Astronautical,Sciences,pp.111-120,Univelt,San Diego,1991.
[18]Cristiano Fiorilo De Melo.Othon Cabo winter.Alternative Paths To Earth-Moon Transfer.Mathematical Problems in Engineering.Volume 2006,Article ID 34317,Pages 1~20 DOI 10.1155/MPE/2006/34317.
[19]Roger R.Rate,Donald D ,Mueller,Jerry E.White.Fundamentals of Astrodynamics[M].Dover Publications.Inc,New York ,1971.
[20]高玉东.月球探测器地月空间转移轨道研究[D].长沙:国防科技大学,2008.
[21]陈海萍.载人登月任务中止轨道研究综述[J].太空探索,2006年11期.
[22]刘林.航天器轨道理论[M].北京:国防工业出版社,2000.
[23]Shane B.Robinson and David K.Geller.A Simple Targeting Procedure for Lunar Trans-Earth Injection.AIAA Guidance,Navigation, and Control Conference.August 2009,Chicago,Illinois:10-13.
[24]范嵬娜.国外载人登月飞行模式特点[J].国际太空,2011,4:56-59.
[25]盛英华,张晓东,梁建国,赵金才.载人登月飞行模式研究[J].宇航学报,2009,30(1):1-7.

