变速变桨风力发电系统的鲁棒H2/H∞多目标控制

王晓兰，倪昊

（兰州理工大学 电信学院，甘肃 兰州 730050）

0 引言

风力发电系统是一个复杂的，强非线性的动态系统。风能是一种随机能源，大规模风电场输出功率的不可控性，给并网带来了新的挑战。当风速达到额定风速后，一般通过桨距角的有效控制，使系统的输出功率恒定。这方面的研究在国内外已经广泛开展，并取得了一定的成就［1－4］。文献［1－2］对风力发电系统进行了机理建模，应用H∞控制理论设计了桨距角控制器，仿真表明该控制器能够实现风速变化时发电机转速和输出功率的稳定，但是在控制器的设计中没有考虑系统运行过程中机械载荷。文献［3］采用基于动态逆的非线性内模鲁棒控制方法，进行了桨距角控制律的设计，使得系统在工况点变化时，仍然能够保持稳定的功率输出，但这种方法增加了系统的复杂性。文献［4］基于实际的非线性风机模型设计了一种桨距角鲁棒控制器，对参数化和非参数化的扰动都有较强的鲁棒性，但是在风速扰动较大时，桨距角调节器需要频繁动作来维持风电系统的功率水平，增大了系统的机械载荷。文献［5－7］应用鲁棒多目标控制方法设计了桨距角控制器，仿真结果表明在控制器作用下，系统的输出功率都可以得到有效的控制，但是在控制器的设计中没有考虑变速风力机轴系中的阻尼。文献［8］将风力发电系统转化为两质量模型，应用一种非线性控制方法设计了变速风机的桨距角控制器，然而当模型参数发生变化时，系统的性能变差，鲁棒性降低。因此，在风力发电系统中，在保证输出功率有效控制的基础上，如何兼顾机械载荷的减小，从而延长机组的工作寿命是一个需要进一步研究的问题。

本文对风力发电系统进行了机理建模，根据系统输出功率平滑和减小机械载荷的要求，采用鲁棒多目标控制方法设计控制器，应用H2性能指标保证系统输出功率平滑，应用H∞性能指标使系统的机械载荷最小。通过极点配置，满足系统的动态性能要求。利用LMI方法求解，得到桨距角控制器，仿真结果验证了该控制器的有效性。

1 风力发电系统模型

由于电磁时间常数远远小于机械时间常数，因此在本文的研究中，忽略了发电机电磁响应的动态过程。变速变桨风力发电系统主要由三个子系统组成:空气动力机构，传动机构和发电机。变速变桨风力发电系统的结构如图1所示［1］。

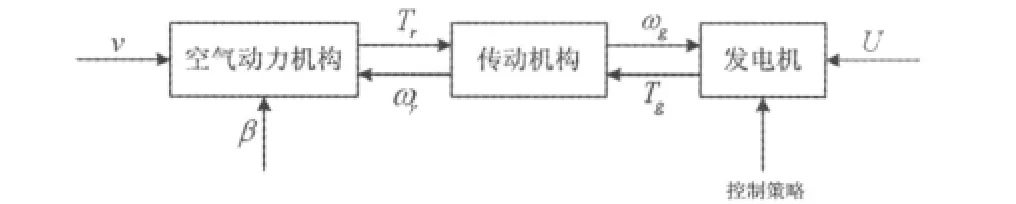
图1 变速变桨风力发电系统结构图

1.1 空气动力系统

空气动力系统用于描述将风能转化为风机功率输出的过程，其能量转换公式为:

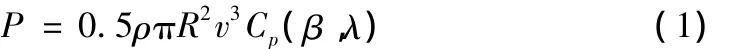
式中:ρ为空气密度，R为风机叶片半径，v为风速，Cp表示风能的转换效率，λ表示叶尖速比，λ=ωr/v，ωr为风机的机械角速度，β表示叶片桨距角，P表示风机吸收风能的功率。

风力机由空气动力中获得的转矩为Ta，其大小表示如下，

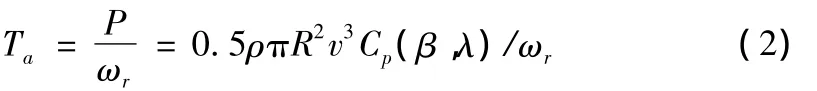
功率系数Cp采用文献［1］中的特性曲线。

1.2 风力机

风力机的动态模型可以表示如下:

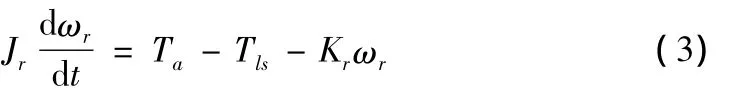
其中:Jr为风轮转动惯量与主传动轴转动惯量之和;Tls为主动轴的扭矩;Kr为阻尼系数。

1.3 传动系统

将传动系统看作两质量模块，假定次传动轴及齿轮系都是刚性的，而所有的柔性都集中在主传动轴上，其柔性用弹簧与阻尼器的并联来表示，则主动轴的扭矩可以表示为:

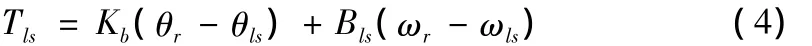
其中:θr为风力机的角位移;θls为低速齿轮的角位移;Kb为主传动轴的弹性系数;Bls为主传动轴的阻尼系数;ωls为主传动轴角速度。

齿轮系的传动比为:

其中，ωg为次传动轴角速度;Ths为次传动轴的扭矩。

1.4 次传动轴与发电机

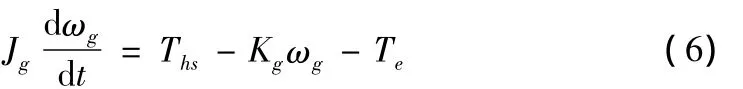
其中:Jg为发电机转动惯量与次传动轴的转动惯量之和;Kg为发电机系统的阻尼系数;Tε为发电机的电磁转矩。

根据式（1）～（6），令 θ=θr－θls，可以得到系统的状态方程模型:

次传动轴上的动态系统可以表示如下:

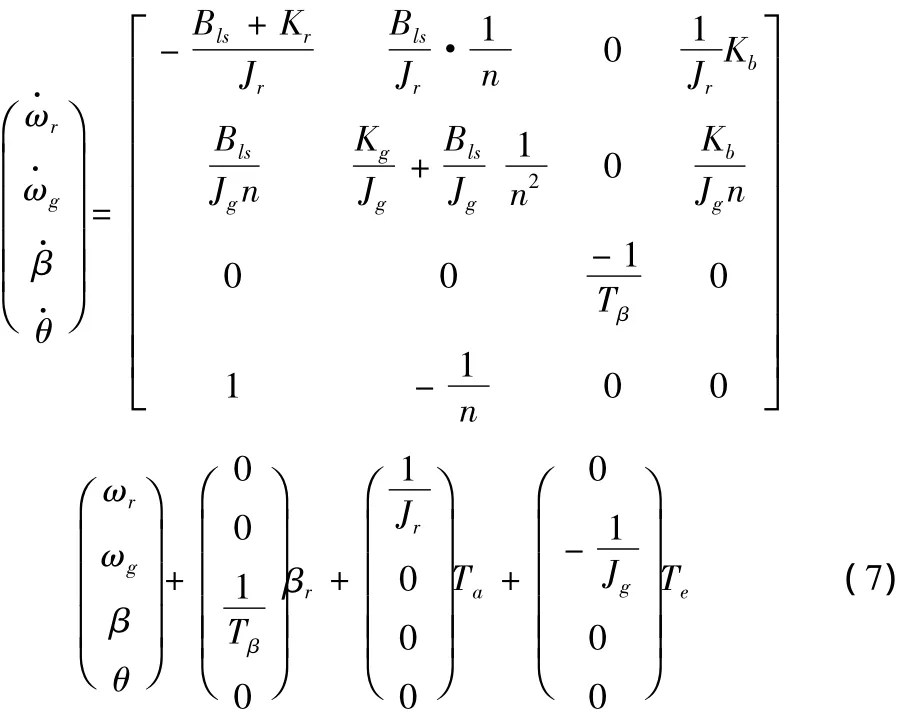
其中，βr是桨距角的参考输入。Ta在（2）式中已定义，其大小与风速v的三次方和风能转换效率Cp的乘积成正比，而Cp是关于桨距角β和叶尖速比λ的非线性函数，因此该模型呈现出强非线性。

风力机工作在额定风速以上时，要求系统输出功率恒定，即稳态运行时风电机组的转速和电磁转矩均维持在额定值。因此我们可以设定电磁转矩为额定值不变，通过调节桨距角来实现发电机的转速调节，从而实现恒功率输出。选取控制输入为桨距角变化量Δβ，把风速变化Δv看作是干扰输入，对以上模型在选定工作点处线性化，可得系统的线性化模型如下:

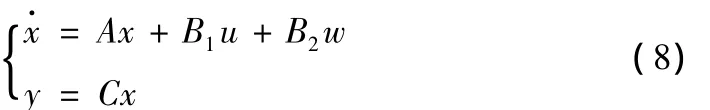
其中，x是工作点处各状态的变化量，即x=Δq，q=［ωrωgβ θ］，u=Δβ，w=Δv，y=Δωg。

2 鲁棒多目标控制器设计

应用H2/H∞和极点配置的多目标控制算法设计控制器，使得系统满足如下要求

（1）减小风速变化对系统输出功率的影响;

（2）减小风力发电系统运行时的机械载荷;

（3）发电机转速保持在恒定值。

第一个控制要求可以由H2准则来满足，相当于在一段时间内使得风速变化对输出功率的影响最小。而减小风力发电系统运行时机械载荷的要求可以通过H∞准则来实现。

2.1 风力发电系统的H2/H∞控制

风力发电系统H2/H∞控制问题如图2［9］，用输出 Δθ表示系统的H∞性能，输出［ΔωrΔβ］表示系统的H2性能，定义性能指标向量如式（9），该性能指标向量第一项Δθ是主传动轴与次传动轴上的扭距差的变化量，第二项［ΔωrΔβ］T是主传动轴的角速度变化量以及桨距角变化量。

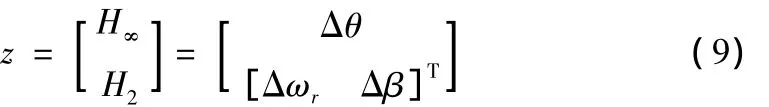
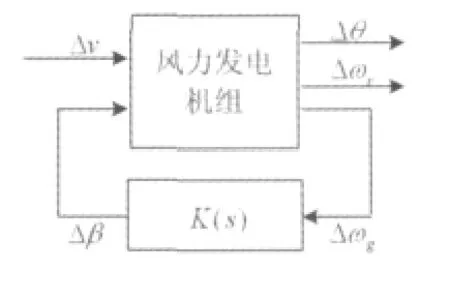
图2 风力发电系统H2/H∞控制问题

控制问题转化为如下的优化问题，即:

其中，T∞是 Δv到 Δθ的传递函数矩阵，T2是 Δv到［ΔωrΔβ］的传递函数矩阵，其定义为:

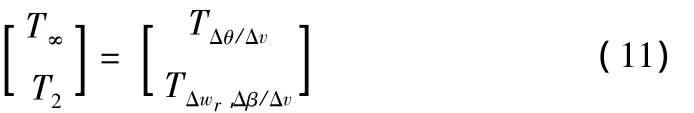
2.2 风力发电系统的极点配置

为了使系统动态性能满足要求，保证最小阻尼比ζ=cosα，如图3。通过极点配置算法使系统的极点处在如图3所示的阴影区域。

2.3 鲁棒多目标控制问题的求解

由式（7）～（9），系统的状态空间模型可以转换为如下形式:

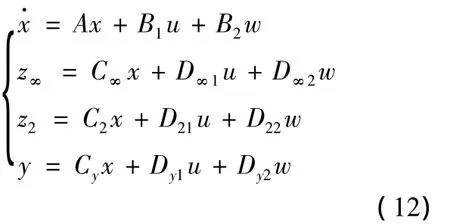
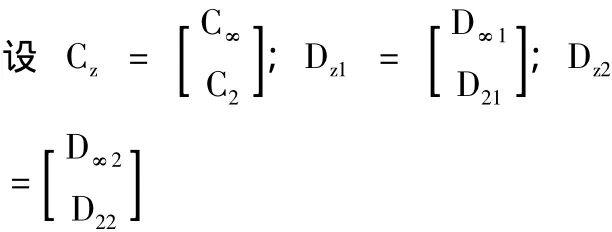
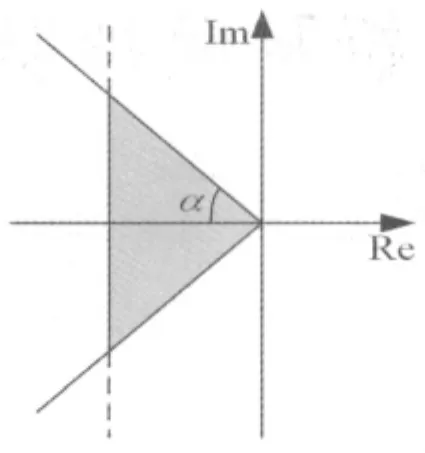
图3 极点配置区域

式（12）转化为:

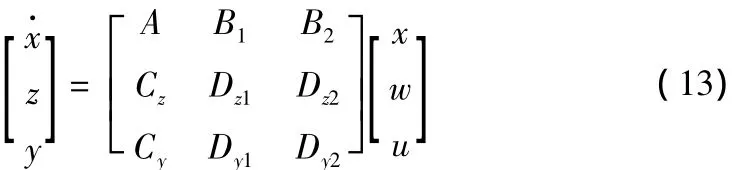
其更一般的形式如下:

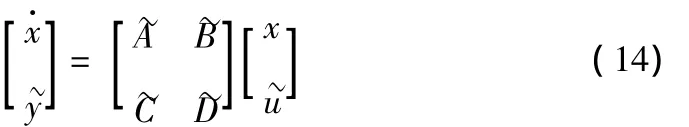
其中:

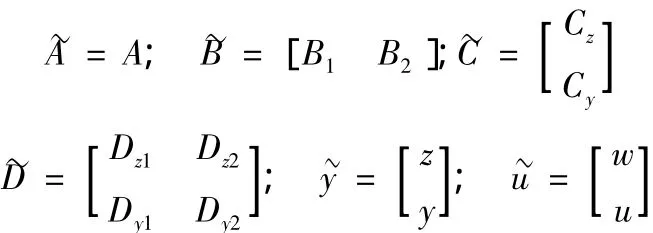
根据式（9）～（12），应用MATLAB的LMI工具箱可以求得该系统的鲁棒控制器。

3 仿真实验

仿真选取水平轴、上风向的三叶片风机，风力发电系统的主要参数如下:额定风速为11.4 m/s，切入风速为3 m/s，切出风速为25 m/s，叶轮半径为63 m，风机额定转速为12.1 r/min，齿轮箱传动比为97，发电机额定转速为1 173.7 r/min，风机转动惯量为1.23 ×107 kg·m2，发电机转动惯量为 534.12 kg·m2。在风速 v=12 m/s处，将系统模型（7）线性化。

当风速发生由12 m/s至 13 m/s的单位阶跃扰动时，开环风力发电系统响应曲线如图4所示。

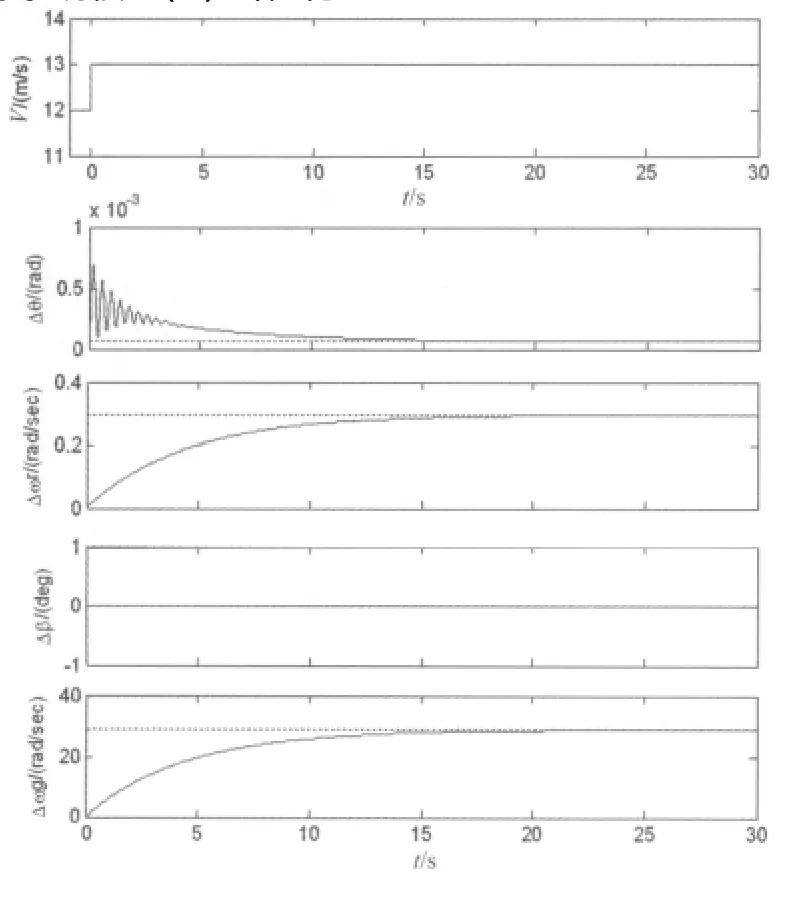
图4 开环风力发电系统对阶跃扰动响应

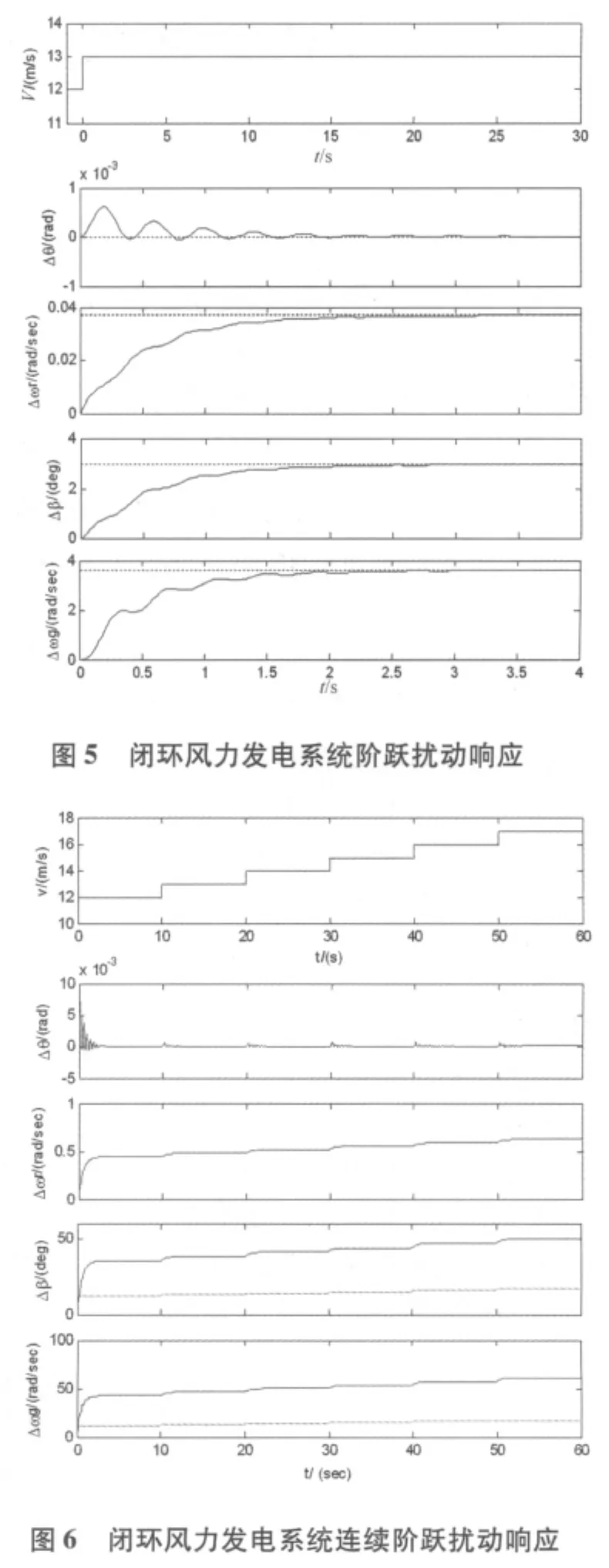
由图4可以看出，在未加控制器时，风力发电系统的主传动轴与次传动轴的扭矩差的变化Δθ较大，波形的振荡明显。图 5是在鲁棒控制器作用下，风力发电系统的对单位阶跃扰动的响应。可以看出风力发电系统的主传动轴与次传动轴的扭矩差变化Δθ有一定的减小，振荡次数减少，系统调整时间由原来的15 s减小到大约3 s。主动轴上的角速度变化 Δωr从 0.3 rad/s减小到0.038 rad/s。可见在控制器作用下，系统的动态性能得到改善，机械载荷得以减小。

当风速发生连续单位阶跃扰动变化时，在鲁棒控制器作用下，风力发电系统的动态响应如图6所示。主动轴角速度变化Δωr和发电机角速度变化Δωg都较小，说明风速变化对系统输出功率的影响较小，同时较小的Δθ保证系统运行过程中较小的机械载荷。

4 结束语

本文采用鲁棒H2/H∞多目标控制方法对额定风速以上的风力发电系统进行了研究。首先建立了风力发电系统模型并在给定的工作点处对其进行线性化得到系统的线性模型，然后综合出鲁棒H2/H∞多目标控制问题，应用MATLAB的LMI工具箱设计得到桨距角控制器。仿真结果表明该控制器能够减小风速变化引起的风电系统运行过程中的机械振荡，在风速突变时，系统能够快速调节桨距角从而保证平滑输出功率，调节过程平缓，有效减小了机械载荷。

［1］张先勇，吴捷，杨金明，等.额定风速以上风力发电机组的恒功率H∞鲁棒控制［J］.控制理论与应用，2008，25（2）:321 －328.

［2］肖劲松，倪维斗，姜桐.偏航时风力机组鲁棒控制器的设计［J］.太阳能学报，1997，18（3）:337 －345.

［3］刘吉宏，吕跃刚，徐大平.风力发电机组桨距角鲁棒控制器的设计与仿真［J］.计算机仿真，2010，27（3）:267 －270.

［4］耿华，杨耕.变速变桨距风电系统的功率水平控制［J］.中国电机工程学报，2008，28（25）:130 －137.

［5］ B.Boukhezzar，L.Lupua，H.Siguerdidjane，M.Hand.Multivariable control strategy for variable speed variable pitch wind turbines［J］.Renewable Energy，2007，32（7）:1273 －1287.

［6］ B.Boukhezzar，H.Siguerdidjane.Robust multi－ objective control of a variable speed wind turbines［D］，SUPELEC，2007.

［7］ Liu Ji-hong，Xu Da － ping.Yang Xi－ yun.Multi－ objective power control of a variable speed wind turbine based on H∞theory［C］.Proceedings of the Seventh InternationalConference on Machine Learning and Cybernetics，Kunming，12 －15 July 2008.

［8］ B.Boukhezzar，H.Siguerdidjane.Nonlinear control of a variable－speed wind turbine using a two － mass model［J］.IEEE Transactions On Energy Conversion，2011，26（1）:149 － 162.

［9］俞立.鲁棒控制（线性矩阵不等式处理方法）［M］.北京:清华大学出版社，2002.