特定输出功率下表皮能量传输系统优化设计

刘超，唐厚君，白亮宇，王伟

（1.电力传输与功率变换控制教育部重点实验室 上海交通大学电子信息与电气工程学院，上海 200240 2.河北省唐山市曹妃甸实业港务有限公司，河北 唐山 063000）

0 引 言

医用植入型设备，包括左心室辅助装置（LVAD）、心脏起搏器、心律转变器和植入式心脏除颤器（ICD），人们用这些植入型设备来从体内控制并治疗疾病［1-2］。但这些体内装置因为能量不足而发生故障。传统的充电方式是将导线刺穿皮肤为设备补充电能，这种方式极有可能导致皮肤感染，同时也会为病人的日常生活带来很大的不便。图1给出了不同植入型医疗设备的电能消耗情况。

表皮能量传输系统（TET）可以通过空间时变的磁场透过皮肤将电能从一次侧能量源传输到二次侧能量接收端。图2给出了一个典型的TET系统的示意图，系统体外部分产生的磁场使得体内部分产生感应电压，并利用这个感应电源来为设备充电。

图1 不同植入型设备电能消耗情况

已经有很多学者对TET系统的优化设计进行了研究分析，也对很多目标函数进行了优化，例如最大传输功率和传输效率。首先，针对最大传输功率的提高，人们提出了几种优化理论。其中WU.H.H提出调节电容值以最大化传输功率，所得到的最大传输功率值可以达到传统方式的三倍。但与此同时，传输效率却发生了大幅的下降［3］，Chwei-Sen Wang使用电感-电容-电感所建立的谐振变化器拓扑结构来最优化传输功率［4］。

其次，对于传输效率的提高，Stanimir Valtchev提出了一种新的理论，来对串联型谐振变化器进行仿真分析，大大提高了松耦合变压器分析的准确性［5］。

如果对TET系统的一二次部分的互联关系进行一个详细的优化设计，很难获得令人满意的效果。为此，第二部分给出了TET系统设计中的互感耦合模型和相关参数。第三部分则根据频率分叉现象和元件耐压耐流等条件，对TET系统最优化模型进行了详细的分析。第四部分通过遗传算法对非线性约束模型进行了最优化分析。

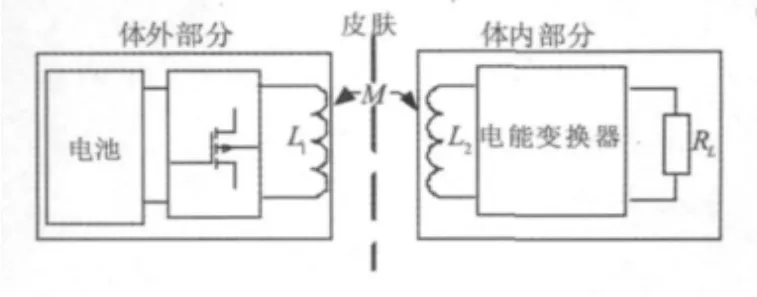
图2 TET系统电路图

1 TET系统的电气模型

TET系统隔着皮肤，通过相互独立的互感线圈对电能进行传输。

图3中，jωMi2是二次电流i2在体外设备中感应出的电压，jωMi1是由一次侧电流i1在体内感应出的电压。M是一二次侧设备的耦合系数，ω是系统运行的角频率。Zr是体内植入端感应到体外设备的阻抗，Zs是体内植入端的独立阻抗。r1和r2分别是一次和二次侧电阻，下表1和2分别代表一次侧和二次侧。对于其他三种拓扑结构：“串-串”，“并-并”“并-串”，其优化模型是相似的。文献［4］给出了其他几种拓扑的分析。

TET系统的电压Ui是一个方波电压，由图3中所示的H桥逆变器提供。

从一次设备传输到二次设备的功率P2可有以下公式计算出：

图3 TET系统互感耦合模型

其中，Zin是从电源端等效得出的负载阻抗幅值。

过低的电能传输效率不仅仅缩短了TET系统的寿命，还会产生严重的发热问题，并带来健康隐患，例如过多热量的产生和扩散会导致机体组织的受损。因此传输效率的提高对实际应用有着非常重要的意义。并且，要实现设备的轻型化，同时将发热降到最低，必须有效降低设备线圈损耗，而降低损耗最有效的方法就是提高效率。

因为TET系统工作频率非常高，在实际应用中不得不考虑肌肤效应的影响。通常情况下，双绞线比实心线的交流阻抗低。不仅仅是肌肤效应，邻近效应也会大大减少。因此选用双绞线绕制一二次线圈。

TET系统的传输效率是成功输送到二次侧设备的电能总量，与从一次侧电源输出的电能总量的比值。其公式可以写为：

理论上，系统应工作在二次侧谐振频率点上：ω＝1／，系统电能传输效率可以转化为：

其中，k＝M／为系统耦合系数。

由公式可知，电能传输效率是线圈电感、耦合系数和线圈阻抗的函数。

2 TET系统优化模型

对于TET系统而言，要想获得很好的电气性能，详细的参数优化是必不可少的。这一部分将给出TET系统的优化模型，包括设计变量、优化目标函数和优化约束条件。其中L1和L2是设计变量，它们会随着优化进程的进行而发生变化。

该模型对系统的最大传输功率和传输效率进行优化。在临床应用中，医用植入型设备的能耗为10～30W［6］，因此在这个功率等级下对系统传输效率进行优化具有更为实际的意义。

约束条件

（1）基于频率分叉现象的不等式约束。在对系统进行优化的过程中，在频率分叉区中运行频率的稳定性始终是不可忽视的［4］，在频率分叉区中，系统工作频率很有可能偏离理想运行点，进入不稳定状态。因此，优化模型必须保证所分析的参数远离频率分叉区域。

对于“串-并”补偿拓扑而言，频率分叉界限为［5］：Q1＞Q2＋1／Q2，其中Q1和Q2是一二次侧的品质因数。频率分叉区域可以用以下公式描述：

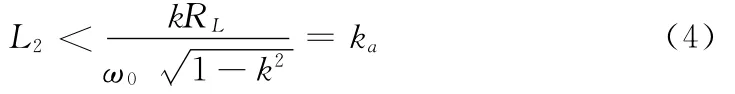
从公式中可以看出，二次侧电感值L2决定了系统是否处于频率分叉区中，而一次侧电感则与该约束条件无关。当二次电感值L2比ka大时，就会避免系统发生频率分叉现象。为了更加直观的给出二次电感值对频率分叉现象的影响，图4给出了负载阻抗角随着二次电感值变化的曲线。ka（点划线）是频率分叉界限曲线，如果L2大于ka，则零相角频率是唯一的，等于二次谐振频率，相反，则会出现频率分叉现象。

（2）基于元件最大耐压耐流的不等式约束。要使整套系统达到预期的性能，每个元件都必须正常工作。系统中元件应工作在最大峰值电压和峰值电流的条件下。

如图3所示，I1（L1，L2），V1（L1，L2），I2（L1，L2）和V2（L1，L2）分别为一次侧电流、一次侧补偿电容电压、二次侧电路和二次侧补偿电容电压值。Istress1，Istress2，Vstress1和Vstress2分别为一次和二次侧线圈耐流和补偿电容耐压值。

图4 不同二次侧电感值下频率分叉现象

3 整合优化

本部分给出了系统的优化过程，计算出最优化条件下的一次二次侧电感值，以满足医疗植入型设备的不同要求。为了获得更实际性地设计模型，优化设计中将引入前几部分所讨论的约束方程。同时引入η（L1，L2）作为优化参数，以同时优化传输效率。据此，可将优化问题归结为以下方程组：

其中，ka是L2取值范围的下限，Pgiven是指定的电能传输功率。

图5给出了遗传算法的流程图，遗传算法是一种随机性的搜索技术，可以全局性地找出最优解。通过遗传算法引入约束性最优化方法。使用轮盘赌方法进行结果筛选，并将最优的结果投入下一轮计算中。

为了更详细地描述上面所讲的最优化问题，现在设置四组Pgiven值，分别为10W，20W，30W，40W，见表1。

图5 遗传算法流程图

表1 不同状态下遗传算法的最优化解

为了验证最优化模型的准确性，将所得结果与 MATLAB／Simulink仿真所得结果进行对比。利用simulink软件包对图2所示TET系统进行仿真，仿真参数为：Vdc＝15V，RL＝20Ω，f＝40kHz。表2给出了系统的最大传输功率和传输效率。

表2 不同状态下遗传算法的最优化解

由表2数据可知，仿真结果符合指定的输出功率要求。因此，在稳态情况下，当一次和二次侧电感设置为最优化值时，系统可以准确的输出指定功率。

由此可知，这种最优化方法可以在不影响系统指定输出功率的前提下，大幅提高能量传输效率。

4 结束语

本文以线圈电感为对象，提出了一种在指定传输功率下对传输效率进行优化的约束性最优化方法。提出了基于频率分叉理论和元件最大耐压、耐流条件的约束方程。利用MATLAB／Simulink建立仿真模型，验证了理论的有效性。同时引入遗传算法进行模型分析，遗传算法在简单的计算性整步、最优解收敛和初始值的选择方面表现出了很大的优势。综上所述，本文所提的优化模型很好的在实现指定电能传输功率的前提下，对系统传输效率进行了优化和提高，大大改善了系统的电气性能，降低损耗，有很大的实用性价值。

［1］HALPERIN D，Kohno T，Heydt-Benjamin，et al.Security and privacy for implantable medical devices［J］.IEEE Pervas.Comput.，2008，7（1）：30-39.

［2］Schuder J C.Powering an artificial heart：birth of the inductively coupled-radio frequency system in［J］.Artif.Organs，2002，26（11）：909-915.

［3］Wu H H，Hu A P，Malpas S C，et al.Determining optimal tuning capacitor values of TET system for achieving maximum power transfer［J］.Electron.Lett，2009，45（9）：448-449.

［4］Chwei-Sen，Wang，Covic G A，Stielau O H.Investigating an LCL load resonant inverter for inductive power transfer applications［J］.IEEE Trans.Power Electron.，2004，19（4）：995-1002.

［5］Valtchev S，Borges B，Brandisky K，et al.Resonant contactless energy transfer with improved efficiency［J］.IEEE Trans.Power Electron.，2009，24（3）：685-699.

［6］Dissanayake T D，Hu A P，Malpas S，et al Experimental study of a TET system for implantable biomedical devices［J］.IEEE Trans.Biomed.Circuits Syst.，2009，3（6）：370-378.