双侧向测井响应的有限元法模拟

王欣，陈浩，王秀明，曲敏

(中国科学院声学研究所，北京100190)

1 引言

油气储层评价中的电法测井，主要是通过对井下电法测井仪器测得的视电阻率资料进行处理，反演出地层的真电阻率或者接近于真实的岩石电阻率，配合声波测井和核物理测井，可以最终评价储层中流体的性质和定量评价孔隙中含油饱和度，它是油气储层测井评价中重要的手段。侧向测井是电法测井中常用的一种。1934年，Schlumberger兄弟首次以“监督电极”的方式提出了侧向测井的思想［1］。随后，Doll在1951年提出并完善了侧向测井的概念，发展了三侧向和七侧向［2］。基于前人工作，Suau等人在1972年提出并发展了双侧向(九侧向)测井技术［3］，如图1所示。为了准确得到地层的真电阻率，就需要高精度、高灵敏度的电法测井仪器，而要设计出这样的电法测井仪器，就要了解双侧向测井仪器对实际测井的视电阻率响应特征。由于该仪器结构较为复杂，即便对最简单的地层模型，其响应也没有解析解。

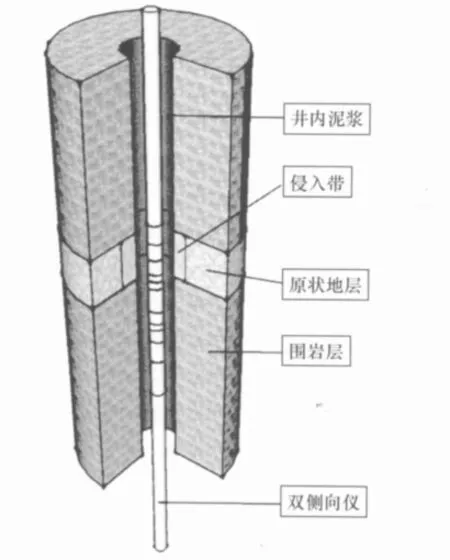
图1 双侧向测井模型

因此只能采用数值的方法来模拟实际的仪器响应，进而优化设计相关电法测井仪器的结构，如仪器的长短、电极系的几何尺寸等等。地层电参数差异较大、侧向测井仪器自身结构复杂的特点，使擅长复杂模型数值计算的有限元方法从一开始就成为人们研究侧向测井问题的最主要手段。但由于有限元在自由剖分网格的同时，会形成一个庞大的稀疏矩阵，计算量非常巨大。为了解决大规模矩阵运算问题，1970年，Irons提出了一种用于有限元分析的波前法(Frontal Solver)［4］。1971 年，Coggon 首次将有限元方法引入电法测井中［5］。1975年，李大潜等人对采用有限元素法进行视电阻率测井数值计算的问题进行了比较系统的考察［6］。1982年，Anderson用有限元法模拟计算了感应测井响应［7］。1986年，张庚骥首次将“波前法”引入电测井问题的有限元模拟中，大大提高了有限元素法在电阻率测井响应数值模拟中的计算效率［8］。1989年，Khokhar利用有限元法对侧向测井在薄地层中的响应进行了模拟计算［9］。1993年，Lovell发展了一种基于频率相关的电位偏微分方程模拟方法［10］。1998年，Chen等人通过有限元的数值模拟方法检验了一种阵列侧向测井模型的分辨率和精度［11］。1999年，Liu等人研究了一种盐水泥浆动态侵入的双侧向测井响应的模型并应用于中国渤海湾油田［12］。2002年，刘振华、胡启利用有限元法对阵列侧向电极系在不同地层模型下的测井响应进行了数值模拟，讨论了井眼效应、侵入特性和层厚影响等问题，对电极系仪器常数的计算也进行了研究［13］，Galli等人介绍了一种由Schlumberger和ENI-Agip共同开发的阵列侧向二维电阻率正反演技术在挪威近海一处碎屑岩储集层的应用情况［14］。2006 年，Michael等人基于 LRI(Localized Rapid Inversion)新方法提出了一种针对阵列侧向测井仪器的实时解释技术［15］。2007年，Cozzolino等人研究了轴对称地层模型中双侧向仪的合成聚焦和模拟［16］，Yang等人用二阶有限元方法解释了中东碳酸盐岩储层的双侧向测井数据［17］，朱军等通过对仪器电极系的改进对高分辨率双侧向测井响应进行了数值模拟分析［18］，范晓敏等对双侧向测井曲线形状的影响因素进行了研究［19］。2008年，仵杰等人利用二维有限元法对阵列侧向测井仪器的响应进行了数值模拟，分析了不同地层模型下目的层厚度和侵入深度变化对测井响应的影响［20］。2009年，范宜仁等利用有限元方法，在二维非均匀介质模型下对阵列侧向测井响应进行了数值模拟，研究了不同层厚、侵入带、井眼条件下阵列侧向测井响应，与双侧向测井响应进行了对比［21］。

本文采用米字型网格，合理分配网格疏密程度和节点编号，在保证精度的前提下提高了程序的运行速度，通过对多种模型参数进行改变，模拟和分析了各种因素对双侧向测井响应的影响，并首次探讨了三种近似处理后的侵入模型下测井响应的特征，为仪器的优化设计及电阻率反演作基础，为测井资料解释方面提供参考和指导。

2 双侧向测井问题的模型建立

双侧向电极系共包括九个电极:中间七个体积较小的环状电极，两端各一个体积较大的柱状电极。如图2所示，A0是主电极，M、M'和N、N'是两对监督电极，A1、A'1是一对屏蔽电极。

图2 电极系模型

当A2、A'2作为一对屏蔽电极时，电极系为深侧向电极系;当A2、A'2作为一对回路电极时，电极系为浅侧向电极系。以主电极为中心，这四对电极对称地排列在两端，每对电极之间用导线连接，因此M和M'电极具有相同的电位，N 和 N'，A1和 A'1，A2和A'2电极也具有相同的特点。所要解决的问题是，在这种双侧向测井仪器结构下，其视电阻率响应是如何受仪器结构、地层参数和井眼参数影响的。数学形式可以归结为:求出一个连续而且适当光滑的位函数U，它满足以下各条件:

(a)在求解区Ω内需要满足式(1):

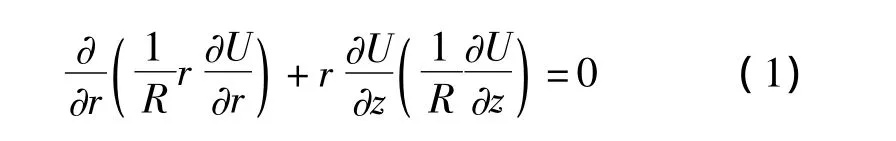
(b)方程采用柱坐标，其中R为介质的电阻率。在恒流电极表面上，需要满足式(2):

其中Rm为泥浆电阻率，IA为恒流电极所供电流，是一已知量，n为边界的外法线。

(c)在绝缘边界，需要满足式(3):

(d)在无穷远边界，需要满足式(4)。

双侧向测井问题的定解形式直接求解起来非常复杂，可转化为泛函极值的形式，其表述为在X中使泛函J(U)取极值(最小值)的函数U。

其中IE和UE为电极的电流和电位。如图3所示，为了保持对称性，采用米字型网格。靠近井眼和原状地层处的网格划分得较密，以保证数值模拟的精确度，围岩及靠近无穷远边界处的网格划分得较稀疏，以提高程序计算效率。

图3 网格剖分

模型的几何尺寸比例尽量保持和实际井下情况一致。编号的合理与否将直接影响程序的运行效率，采用的具体实施过程是:从左至右、自下而上进行编号。把单元电导阵Ge安装到总体电导阵G上。其中，单元电导阵:

其中

{i，j，k}={1，2，3}或{3，1，2}或{2，3，1}。测井时电流调节要保持式(7)成立，

令主电极电流为1，代入式(8)，

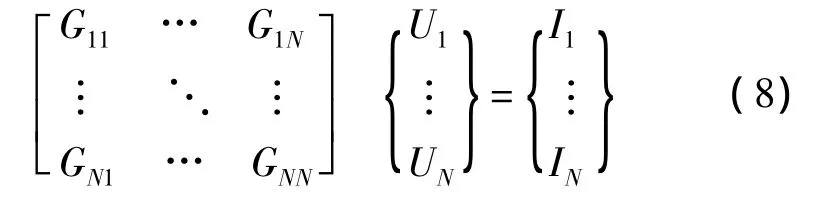
求解式(8)，即可得到求解域的电场分布，求解过程采用的是波前法。

主电极电流为1，当K已知时，将求得的监督电极电位UM代入式(9)，即可得到最终所要求解的视电阻率Ra。因此，在求解视电阻率值时，不必求解出整个电场，只要知道UM即可，这样可以进一步改进线性方程组的求解过程，采用改进后的波前法，编号时将所在节点最后编号，这就可以在边安装边消元的过程完成后，直接得到UM，从而节省大量回代过程，大大提高了程序的计算效率。浅双侧向的情况只要将屏蔽电极A2、A'2改成回流电极即可，具体实施过程这里不再赘述。

3 双侧向测井响应的数值模拟

本文通过正演模拟，研究了多种模型下井眼、侵入带、层厚对双侧向测井响应的影响，探讨了不同侵入模式下的测井响应特征。模型采用的双侧向仪器直径为0.089m，全长为9.36m，电极系尺寸为(单位:m):

计算得到的深侧向仪器常数为0.739，浅侧向仪器常数为1.485。与可查文献中相同模型的K值0.733(深侧向)和 1.505(浅侧向)基本相同［8］，说明程序正确。

(a)井径的影响

如图4a建立模型，取井内泥浆电阻率为1Ω·m，无侵入，原状地层厚度为3m，原状地层电阻率为50Ω·m，围岩电阻率为1Ω·m。井径分别取0.1m、0.2m、0.3m、0.5m，对比深、浅双侧向响应。模拟结果中，目标层浅侧向的响应大于相同条件下深侧向的响应。

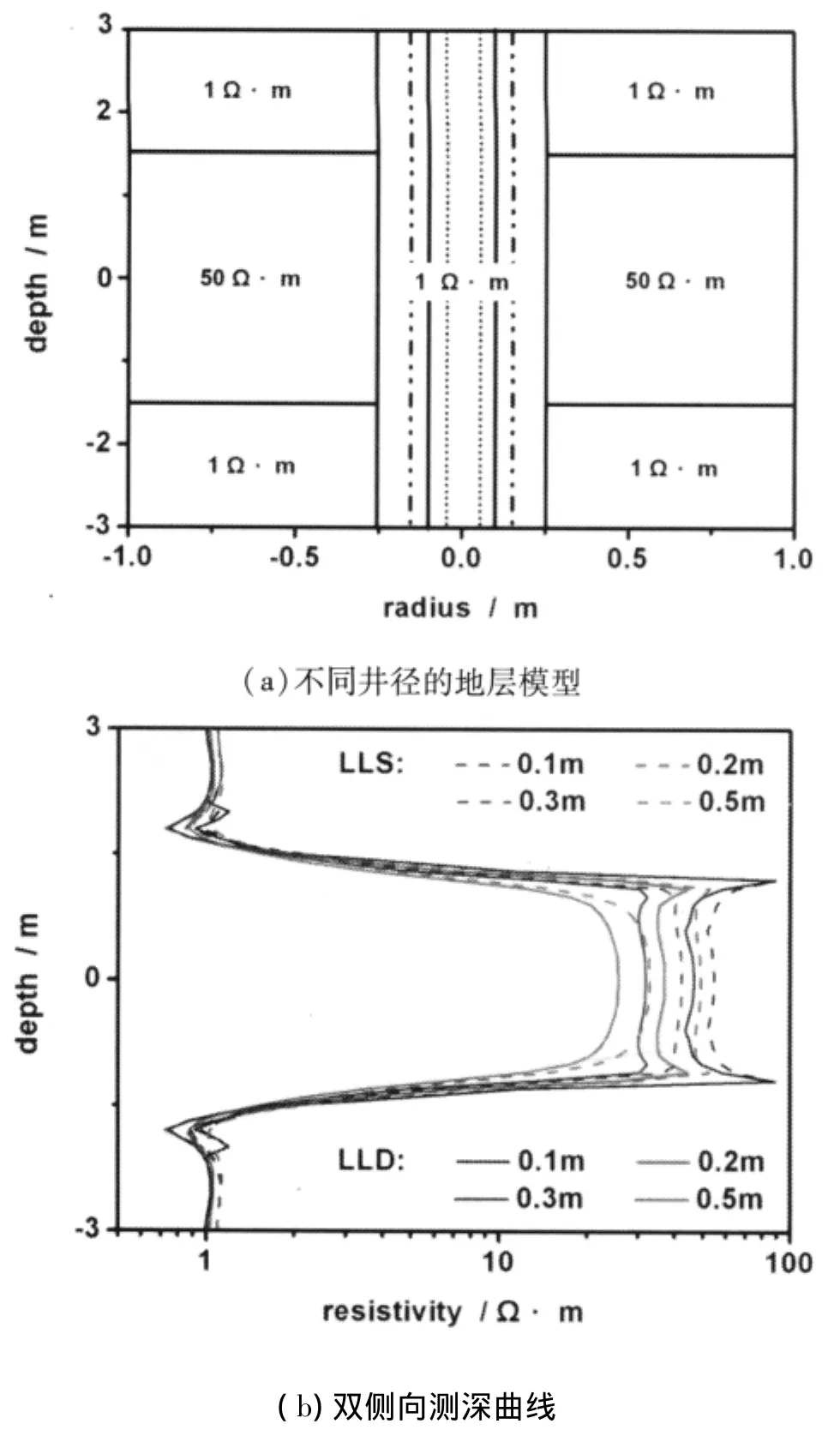
图4 (LLS为浅侧向，LLD为深侧向)

由图4b可知，随着井径的增大，深、浅侧向响应都减小。曲线形状渐趋平缓，双峰现象逐渐消失，低阻地层电阻率模拟值与真实值基本趋于相同。

(b)井内泥浆电阻率的影响

如图5a建立模型，取井径为0.2 m，侵入带厚度为0.3m，侵入带电阻率为2Ω·m，原状地层厚度为3m，原状地层电阻率为50Ω·m，围岩电阻率为1Ω·m。井内泥浆电阻率分别取0.1Ω·m、1Ω·m、10Ω·m，对比深、浅双侧向响应。模拟结果中，目标层浅侧向的响应大于相同条件下深侧向的响应。

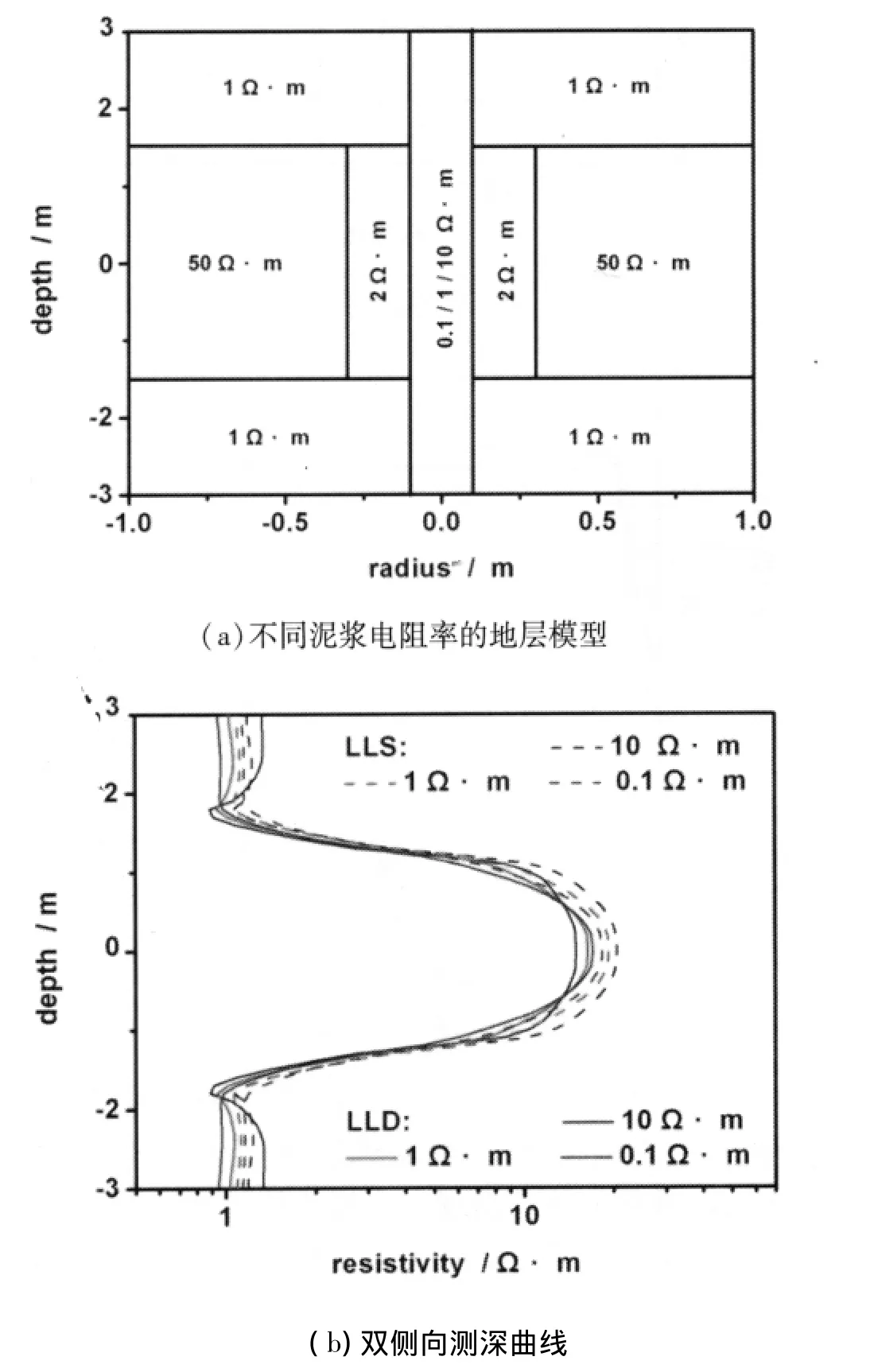
图5 (LLS为浅侧向，LLD为深侧向)

由图5b可知，随着泥浆电阻率的增大，深侧向响应减小，对应的浅侧向响应增大。说明浅侧向受泥浆电阻率的影响较大，变化趋势和泥浆电阻率的变化趋势保持一致。当泥浆电阻率增大时，深侧向受侵入带的影响变大，故其模拟值呈下降趋势。

(c)侵入带厚度的影响

如图6a建立模型，取井径为0.2 m，井内泥浆电阻率为1Ω·m，侵入带电阻率为2Ω·m，原状地层厚度为3m，原状地层电阻率为50Ω·m，围岩电阻率为1Ω·m。侵入带厚度分别取0m、0.1m、0.3m、0.7m、1.1m、1.5m，对比深、浅双侧向响应。

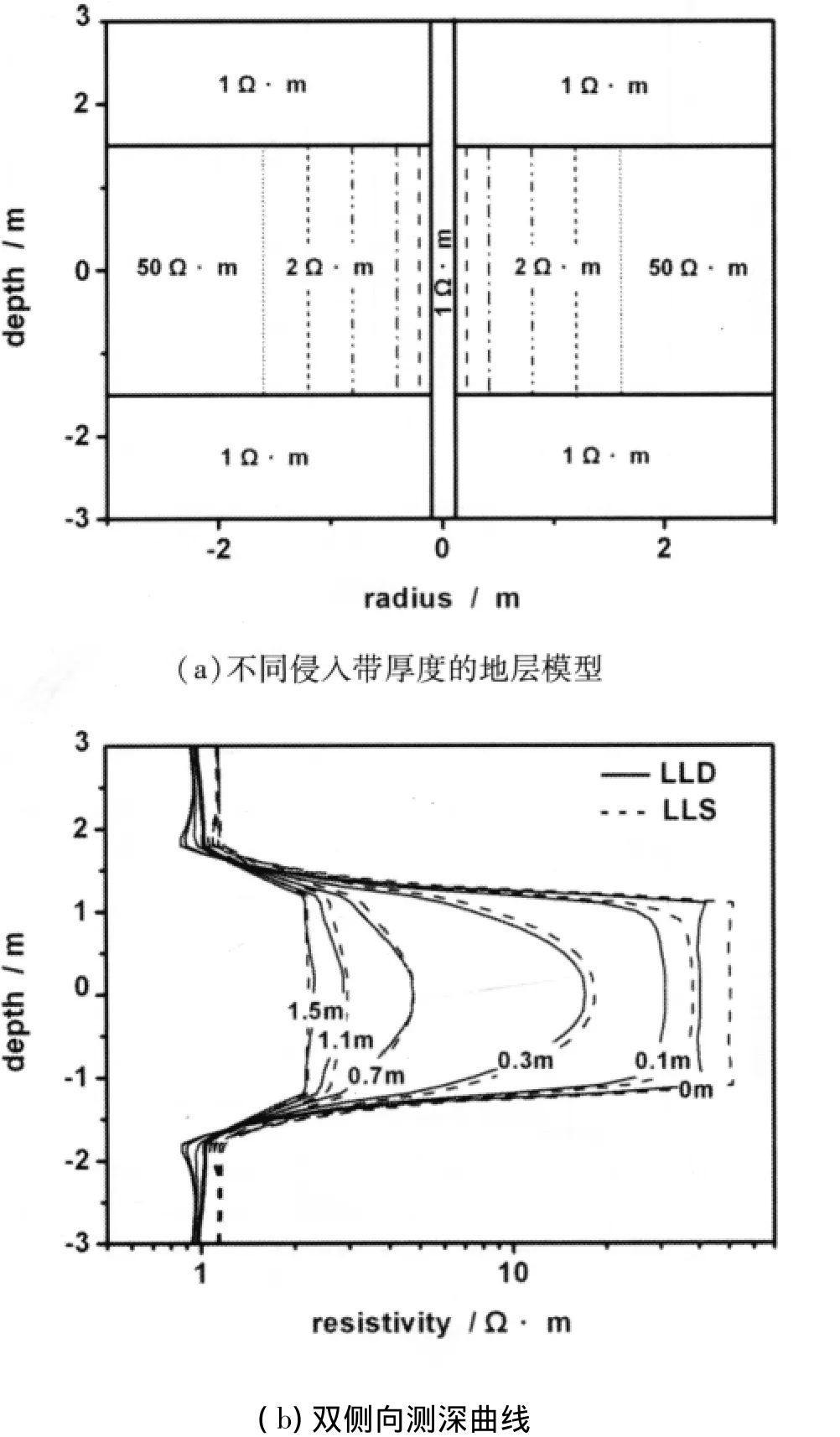
图6(LLS为浅侧向;LLD为深侧向)

由图6b可知，随着侵入带厚度的增大，深、浅侧向响应都减小。当侵入很少时，双峰现象比较明显;随着侵入加深，曲线形状渐趋平缓。当侵入厚度小于1.5m时，浅侧向的响应大于相同条件下深侧向的响应;当侵入厚度大于1.5m时，浅侧向的响应小于相同条件下深侧向的响应。

(d)侵入带电阻率的影响

如图7a建立模型，取井径为0.2 m，井内泥浆电阻率为1Ω·m，侵入带厚度为0.3m，原状地层厚度为3m，原状地层电阻率为50Ω·m，围岩电阻率为1Ω·m。侵入带电阻率分别取1Ω·m、10Ω·m、30Ω·m、50Ω·m，对比深、浅双侧向响应。模拟结果中，目标层浅侧向的响应大于相同条件下深侧向的响应。

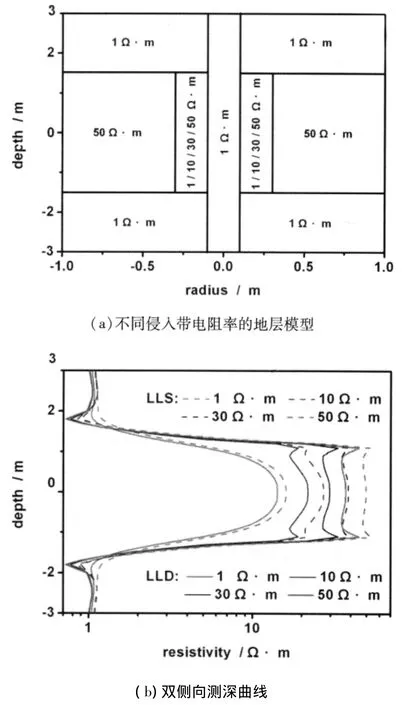
图7(LLS为浅侧向，LLD为深侧向)

由图7b可知，随着侵入带电阻率的增大，深、浅侧向响应都增大，曲线的双峰变得比较明显，在地层交界处出现两个突变，低阻地层出现极小值，高阻地层出现极大值。

(e)层厚影响

如图8a建立模型，取井径为0.2 m，井内泥浆电阻率为1Ω·m，无侵入，原状地层电阻率为50Ω·m。原状地层厚度分别取0m、0.2m、0.4m、0.6m、0.8m、1m、2m、3m、4m、5m、6m、7m、8m、9m，围岩电阻率分别取1Ω·m、3Ω·m、5Ω·m、10Ω·m，对比深、浅双侧向响应。

图8(LLS为浅侧向，LLD为深侧向)

由图8b可知，当围岩电阻率相对原状地层比较低时，其影响很小;当原状地层厚度为0.8m左右时，深、浅侧向响应出现一个极大值;当原状地层厚度小于1m时，深、浅侧向响应都很小;当原状地层厚度大于1m时，深、浅侧向视电阻率值比较能反映原状地层真实电阻率值。

(f)侵入模型的三种近似处理

如图9a建立模型，取井径为0.2 m，井内泥浆电阻率为0.03Ω·m，围岩电阻率为1Ω·m，侵入地层电阻率分布情况如图9b所示。

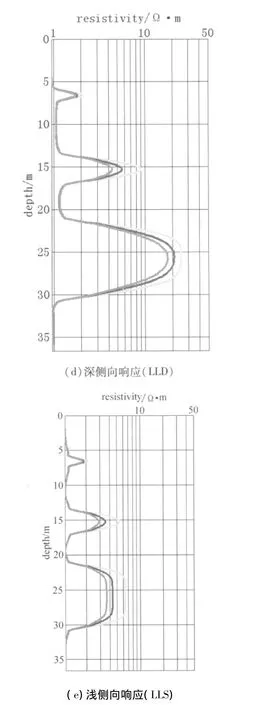
图9

如图9c建立三种侵入模型，对比三种侵入模型下的响应特征可以看出(图9d、图9e)，深侧向测井以终点电阻率为侵入带电阻率更接近于原状地层的真实电阻率，而浅侧向测井以起点电阻率为侵入带电阻率更能反映侵入带的真实电阻率。对比深浅侧向测井响应特征可以看到，浅侧向的纵向分辨率大概为3m左右，而深侧向的纵向分辨率要大于常规测井解释中所认为的3m。如图9a计算7层36m深的地层模型，计算步长为0.2m，共计算181个视电阻率值点，在主频1.81GHz、内存2.00GB的单核台式电脑上的运行耗时大约为4.05s，速度比较快，满足了生产应用中对测井资料精细解释的要求，为电阻率反演工作的有效进行提供了可能。

4 结论

采用米字型网格，对称模型下双侧向测井响应的数值模拟结果也保持对称。模拟7层36m深的地层模型，计算步长为0.2m，共计算181个视电阻率值点，较不分开设置纵向围岩截断边界和纵向侵入带截断边界，分开设置纵向围岩截断边界和纵向侵入带截断边界，模拟速度提高了10倍以上。

随着井径的增大，曲线形状渐趋平缓，深、浅侧向响应都减小。随着泥浆电阻率的增大，深侧向响应减小，对应的浅侧向响应增大。随着侵入带厚度的增大，深、浅侧向响应都减小。当侵入厚度小于1.5m时，浅侧向的响应大于相同条件下深侧向的响应;当侵入厚度大于1.5m时，浅侧向的响应小于相同条件下深侧向的响应。随着侵入带电阻率的增大，深、浅侧向响应都增大。当围岩电阻率相对原状地层比较低时，其影响很小;当原状地层厚度为0.8m左右时，深、浅侧向响应出现一个极大值;当原状地层厚度小于1m时，深、浅侧向响应都很小;当原状地层厚度大于1m时，深、浅侧向视电阻率值比较能反映原状地层真实电阻率值。

深侧向测井以终点电阻率为侵入带电阻率时，计算得到的视电阻率更接近原状地层的真实电阻率;浅侧向测井以起点电阻率为侵入带电阻率时，计算得到的视电阻率更能反映侵入带的真实电阻率。浅侧向的纵向分辨率大概为3m左右，深侧向的纵向分辨率要大于常规测井解释中所认为的3m。

［1］ Schlumberger C，Schlumberger M，Leonardon E G.Electrical coring:a method of determining bottom-hole data by electrical measurements［J］. Petroleum Transactions，AIME，1934(110):237-272.

［2］ Doll H G.The Laterolog:A New Resistivity Logging Method With Electrodes Using An Automatic Focusing System［J］.Petroleum Transactions，AIME，1951(192):305-316.

［3］ Suau J，Grimaldi P，Poupon A，Souhaite P.The Dual Laterolog-Rxo Tool［J］.Fall Meeting of the Society of Petroleum Engineers of AIME，1972:1-44.

［4］ Irons B M.A Frontal Solution Scheme for Finite Element Analysis.Numer［J］.Meth Eng，1970(2):5-32.

［5］ Coggon J H.Electromagnetic and electrical modeling by the finite element method［J］.J Geophysics，1971，36(1):132-155.

［6］ 李大潜，郑宋穆，谭永基.有限元素法在电法测井中的应用［M］.北京:石油工业出版社，1980.

［7］ Anderson B，Chang S K.Synthetic induction logs by the finite element method［J］.23th Ann，The Log Analyst，1982:17-26.

［8］ 张庚骥.电法测井(下)［M］.北京:石油工业出版社，1986.

［9］ Khokhar R W，Johnson WM J.A deep laterolog for ultrathin formation evaluation［J］.30th Ann，Society of Professional Well Log Analysts Logging Symposium，1989:1-10.

［10］ Lovell JR.Finite element method in resistivity logging［D］.Delft:Delft University of Technology，1993.

［11］ Chen Y H，Chew W C，Zhang G J.A novel array laterolog method［J］.39th Ann，The Log Analyst，1998:22-33.

［12］ Liu Z H，Oyang J，Zhang JH.Dynamic duallaterolog responses:model and field applications in the Bohai Gulf of China［J］.J Petroleum Science and Engineering，1999，23(1):1-11.

［13］ 刘振华，胡启.阵列侧向测井响应的计算及其特征［J］.西安石油学院学报(自然科学版)，2002，17(1):53-57.

［14］ Galli M T，Gonfalini M，Mele M.Resistivity Modeling of Array Laterolog Tools:An Application in an Offshore Norway Clastic Reservoir［J］.SPE Annual Technical Conference and Exhibition，2002.

［15］ Frenkel M A.Real-Time Interpretation Technology for New Multi-Laterolog Array Logging Tool［J］.SPE Russian Oil and Gas Technical Conference and Exhibition，2006.

［16］ Cozzolino K，Silva J C.Synthetic focusing and simulation of dual laterolog tool inaxisymmetric subsurface models［J］.J Applied Geophysics，2007，61(2):102-110.

［17］ Yang W，Carlos T V，Ridvan A.Interpretation of frequency-dependent dual-laterolog measurements acquiredin middle-east carbonate reservoirs using second-order finite element method［J］.SPWLA 48th Annual Logging Symposium，2007，1-13.

［18］ 朱军，冯琳伟.高分辨率双侧向测井响应数值模拟分析［J］.石油地球物理勘探，2007，42(4):457-462.

［19］ 范晓敏.双侧向测井曲线形状与地层侵入关系研究［J］.地球物理学进展，2007，22(1):142-146.

［20］ 仵杰，谢尉尉，解茜草.阵列侧向测井仪器的正演响应分析［J］.西安石油大学学报(自然科学版)，2008，23(1):73-80.

［21］ 范宜仁，蒋建亮，邓少贵.高分辨率阵列侧向测井响应数值模拟［J］.测井技术，2009，33(4):333-336.