模拟摩擦接触问题的新型无网格数值方法

马文涛 ，师俊平，李 宁

（1. 西安理工大学 土木建筑工程学院，西安 710048；2. 宁夏大学 数学计算机学院，银川 750021）

1 引 言

接触摩擦问题广泛存在于机械、航空航天、土木、水利等工程领域，并且随着对工程结构分析精细程度日益提高的要求，对该问题的准确描述和求解成为难以回避的问题。由于接触边界及其接触状态（分离、黏合、滑移）在计算前均未知，再加之当接触发生后，需要计算摩擦力，接触问题本质上是复杂的非线性问题，所以接触摩擦问题的求解也被认为是固体力学中极具挑战性的问题之一。目前，有限元是求解接触问题最主要的数值方法，常用算法包括拉氏乘子法、惩罚函数法、数学规划法、互补法等。这些方法都需要引入层状单元或节理单元模拟不连续面的局部接触特性。但当接触面移动时（如裂纹扩展），不得不更新界面单元，网格也随之需要重新划分，工作相当繁琐。无网格法是近年来发展速度较快的新型数值方法，它只需要问题域及其边界上的离散节点信息，没有网格依赖性，非常适合求解流-固耦合、高速碰撞、裂纹扩展、局部化等大变形问题，受到计算力学界和工程界的极大关注[1]。Belytschko等[2]采用罚函数法施加接触条件，基于无网格Galerkin法（EFGM）模拟了裂纹在压荷载作用下的扩展问题。庞作会等[3]将Goodman单元引入EFGM模拟岩体不连续面。李卧东等[4]基于EFGM，在接触面上引入罚参数，通过迭代计算，模拟了弹性体与刚体间的接触行为。卢波等[5]指出，无网格法中使用 Goodman单元存在位移模式与假定位移模式不相协调的问题，通过将节理单元的刚度矩阵累加到系统总体刚度矩阵来解决。以上这些方法在计算过程中，均需使用可视准则。该准则认为，问题边界及任何内部不连续面都是不透明的。也就是说，当节点影响域遇到这些边界和不连续面时都将被截断，那些处于不连续线另一侧的节点将会从影响域中删除，导致系统方程的稀疏度大大降低，必须使用更大的影响域尺度来处理。

本文基于单位分解思想，在EFGM的位移模式中增加阶跃函数项和裂尖奇异项，构造无网格不连续位移场函数。然后参考文献[6－7]的作法，将接触摩擦条件转化为包含惩罚因子的线性互补形式，建立求解摩擦接触问题的不连续无网格线性互补模型，利用已经成熟的Lemke算法求解。该模型无需引入可视准则且不需要迭代计算，大大提高了求解效率。

2 无网格不连续位移模式

标准EFGM的位移场近似函数可表示为

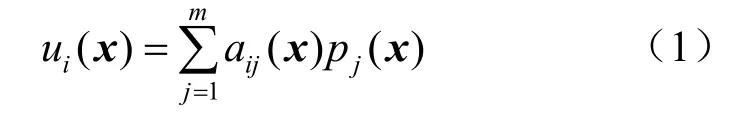
式中：pj为单项式基函数；m为pj的阶次；aij为待定参数，由离散L2范数取极小值的条件确定，具体形式为

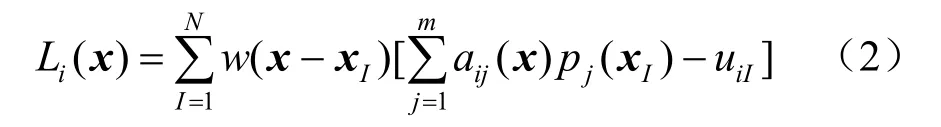
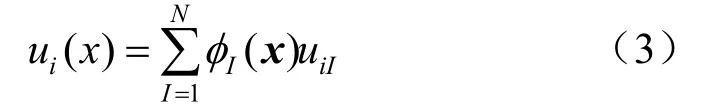
式中：φI(x)为EFGM的形函数，具有高阶连续性、单位分解性等。在处理诸如裂纹等不连续问题时，需考虑由不连续面或线引起的不连续性，因此，必须对式（3）的位移模式进行修改。根据文献[8－9]的结论：若形函数满足单位分解特性，可根据特定问题解的先验知识对近似函数进行扩展。因此，考虑线弹性断裂力学Westergaard解，对EFGM近似函数进行扩展，得到不连续近似函数，具体形式为

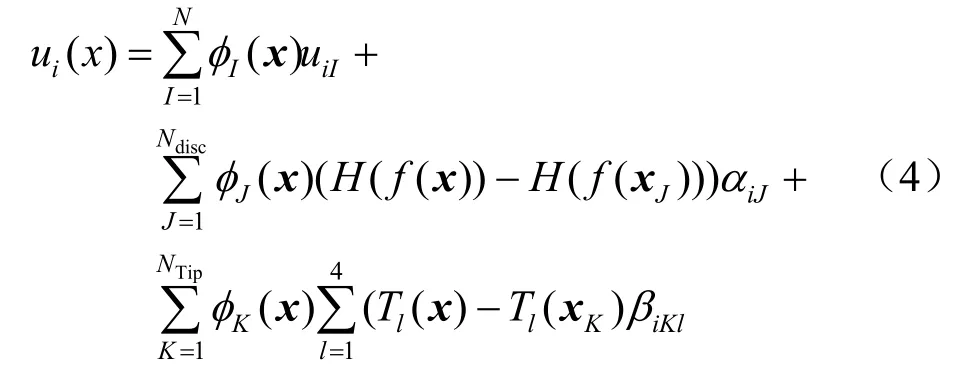
式（4）中第1项是标准EFGM近似函数；第2项反映沿接触面两侧的不连续；第3项则反映接触面端部奇异性。Ndisc为阶跃扩展节点集合，由其影响域被接触面切割的节点组成；NTip为裂尖扩展节点集合，由裂尖的影响域内包含的节点组成；αiJ、βiKl为附加自由度；f(x)为水平集函数，可以隐式表达不连续面，具体形式为

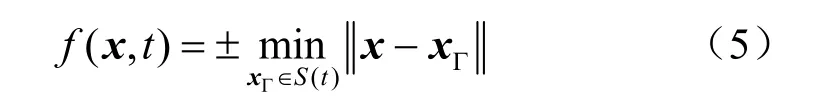
S(t)⊂R2为不连续界面，当节点位于界面上方时取正号，下方时取负号。H(x)为Heaviside阶跃函数，具体形式为

Tl为裂尖扩展函数，表达式为

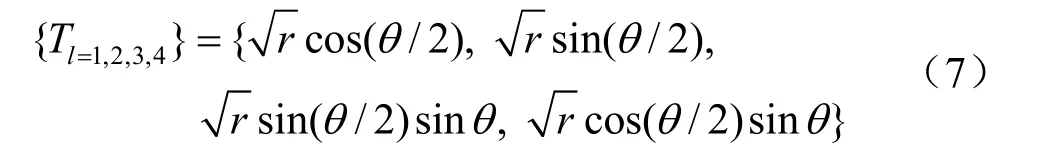
其中：r为节点x到裂尖xTip的距离，

由式（4）可知，计算点的影响域不受结构内部细节的影响，不连续界面引起的位移不连续性由附加自由度确定，无需使用可使准则。

3 接触面方程

为简单起见，考虑二维小变形情况下的面-面接触。设ΩA，ΩB为两个物体组成的接触体系，潜在接触边界为Γc。接触面上对应点的位移定义为和法向和切向接触应力分别定义为pn，pτ。则接触位移用相对位移描述

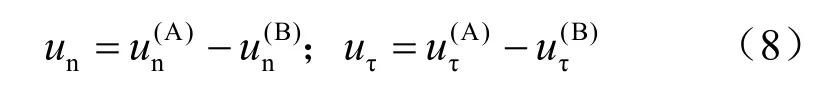
通常，接触力和接触位移应当满足如下两个定律：

（1）法向接触定律

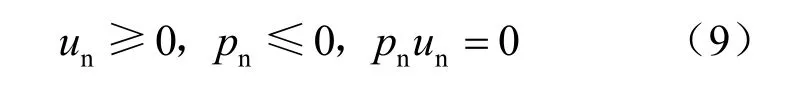
式（9）中3式的意义依次为非穿透条件、法向不受拉条件和互补条件。

（2）切向Coulomb 摩擦定律

式中：μ为摩擦系数；c为黏聚力。参照理想刚塑性体单向应力-应变关系的表述，式（9）、（10）可统一表述为

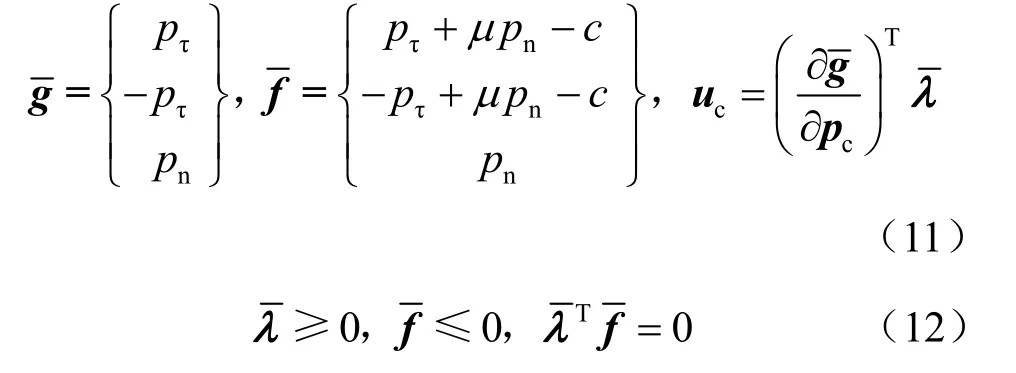
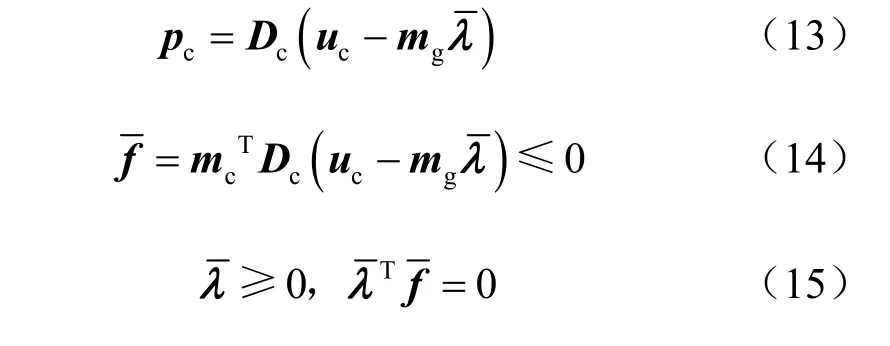
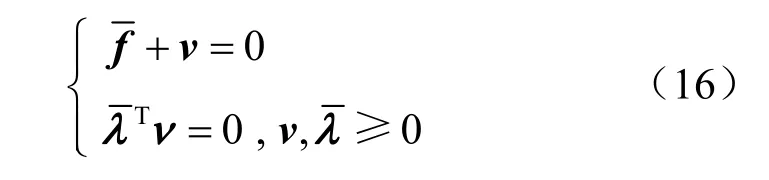
考虑接触面条件，标准EFGM的虚功方程修改为

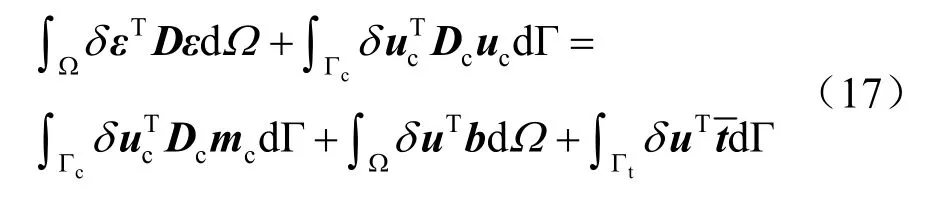
4 离散控制方程

式（17）含有接触面上的积分，因此，必须对接触面进行离散。将接触面划分为有限个区段。每个区段两侧布设相同数目的高斯点，组成接触点对。对于某一接触点对，由式(4)可求得其相对位移为

式中：Bstd由式（3）的形函数导数组成；Benr由扩展部分组成，当 xI∈NDsic时，ΨI(x)为阶跃扩展函数 H(f (x ))-H(f (xJ))；当 xI∈NTip，ΨI(x)分别为裂尖扩展函数为节点位移列向量集合，包括节点常规自由度和附加自由度；

将式（18）代入式（16）的互补条件，可得

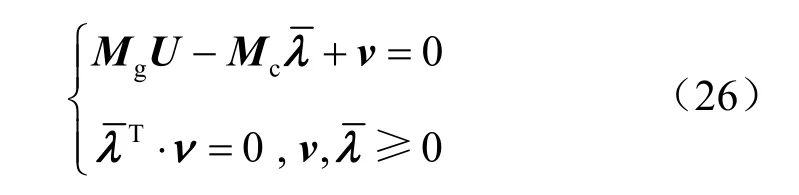
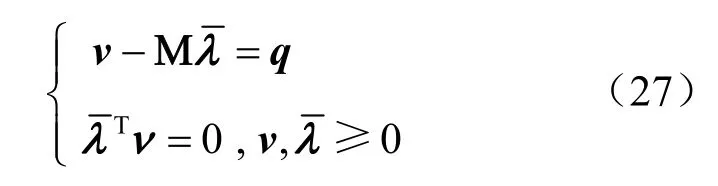
5 数值算例

5.1 含节理平板

如图1所示，宽为1 m、高为3 m的平板，中间含有一条贯通节理，底部固定，上部受均布压力σ和切向力τ的作用。平板材料参数弹性模量为E =2 kPa，泊松比为v = 0.3，节理面摩擦系数为μ = 0.3，凝聚力为c = 0。将整个计算区域划分为21×31个背景积分网格，网格角点为节点，采用4×4高斯积分。将节理面划分为20个区段，每个区段采用4个高斯积分点。首先计算σ = 50 N/m，τ = 0时的情况。当惩罚因子En= Eτ的取值依次选取为E～1012E，计算的法向接触应力值与精确解（σ = 50 N/m）均吻合得很好，最大相对误差仅为0.77%（En= Eτ= E时）；图2给出了沿节理面上的法向接触和切向接触应力分布（En= Eτ= 109E时）。可以看出，本文计算的切向接触应力远小于法向接触应力，其分布反对称于节理面。然后计算σ = 50 N/m，τ = 5的情况。图3为沿节理面上的法向接触和切向接触应力分布。可以看出，切向接触应力为抛物线型分布，法向接触应力为线性分布。以上两种情况的计算结果与文献[7]十分接近。

5.2 受压裂纹应力强度因子

如图4所示，裂纹试样尺寸为50 mm×50 mm，裂纹半长为a = 5 mm，裂纹中心位于试样中心。材料参数取为E = 5 GPa，泊松比v = 0.35，摩擦系数μ = 0，抗拉强度为σt= 3 MPa。试样顶部和底部施加均匀的单轴压缩荷载σ = 1 kPa。节点离散见图4。在裂纹面光滑情况下，该问题的应力强度因子的理论解[10]为

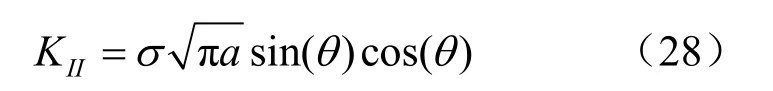
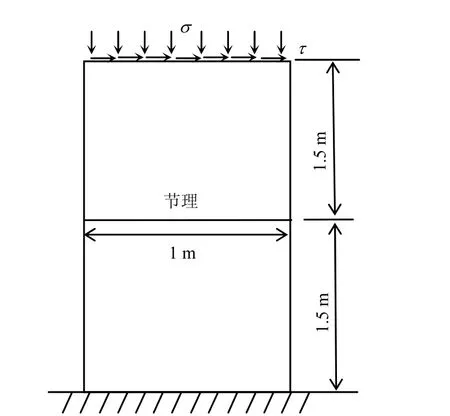
图1 含节理方板Fig.1 A rectangular plate with a joint

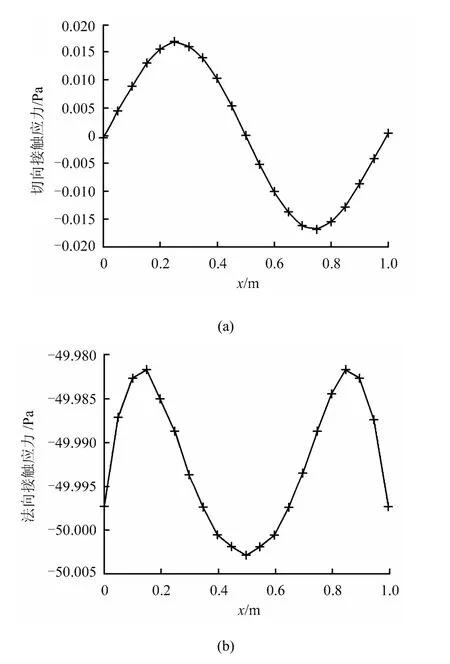
图2 σ =50 N/m，τ = 0时节理面接触应力Fig.2 Contact stresses on the joint face for σ = 50 N/m, τ=0

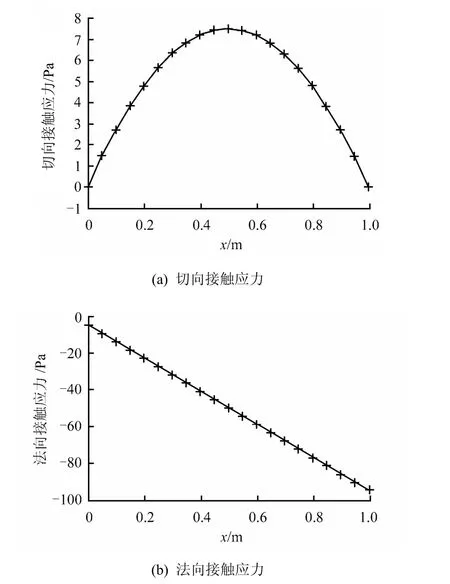
图3 σ =50 N/m，τ = 5 N/m时节理面接触应力Fig.3 Contact stresses on the joint face for σ =50 N/m, τ = 5 N/m

图4 受压裂纹试样Fig.4 Compression-load crack specimen

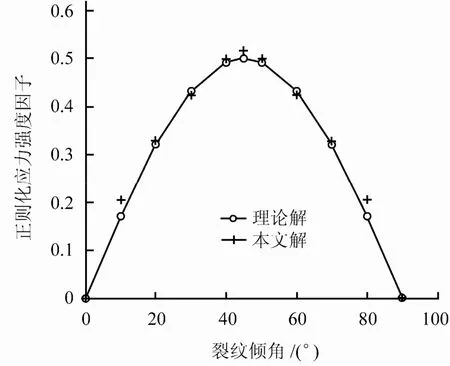
图5 应力强度因子计算结果Fig.5 Computational results of stress intensity factors

5.3 弹性地基中的桩基抗拔问题

本算例分析桩与桩侧土的接触。考虑对称性，选取一半区域计算，计算模型见图6。土为黏性土，其参数为Es= 20 MPa，v = 0.25，ρ = 2 g/cm3。混凝土桩的材料参数为 Ec= 2×104MPa，v = 0.3，ρ=2.5 g/cm3。桩土接触面间满足Mohr-Coulomb定律，凝聚力c = 0.05 Pa，摩擦系数μ = 0.58。底部边界固定，两个侧边施加水平位移约束，桩顶部施加P =5×102kN/m的拉力作用。

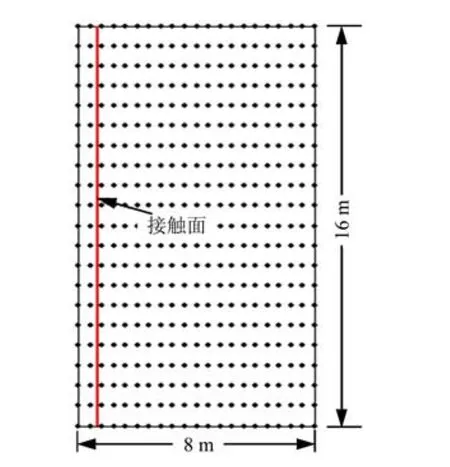
图6 节点离散Fig.6 Node discreteness

图7为本文方法和有限元中使用接触单元[11]计算得到的接触面切向应力分布图。可以看出，与文献[11]相比，本文方法能更好地体现桩基与地基土之间的滑动摩擦将自上而下地扩展的性质。

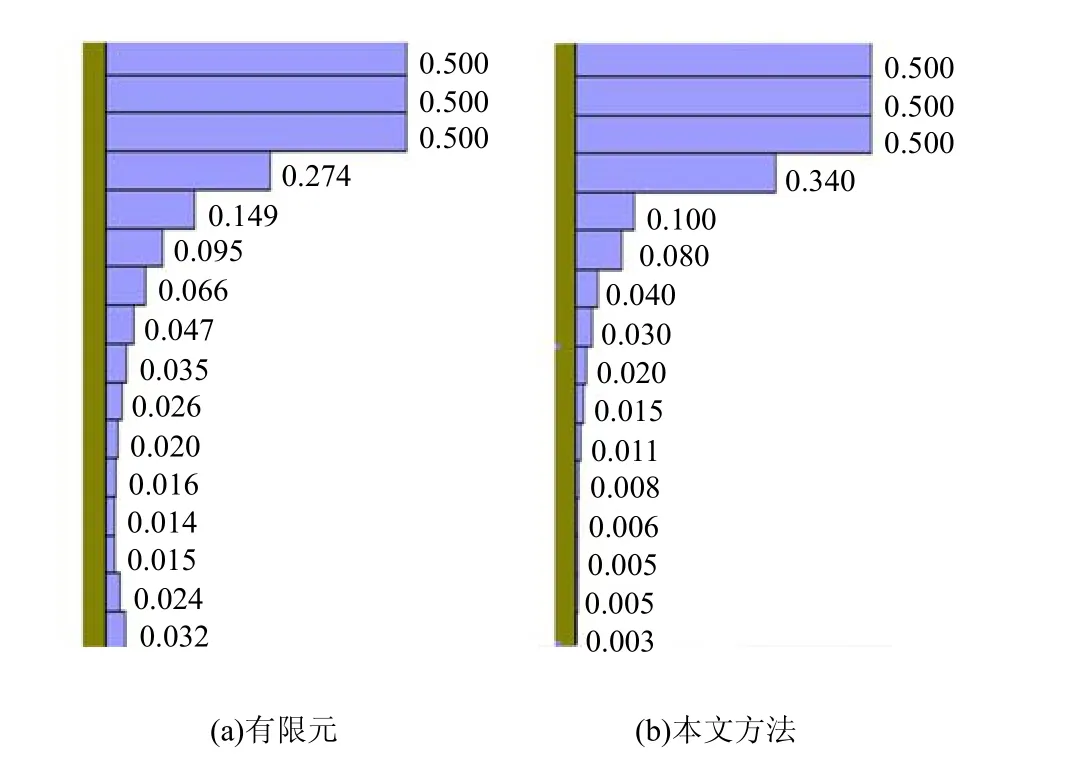
图7 接触面上的剪应力分布Fig.7 Shear stress distributions along contact surface

6 结 论

本文首先利用标准的无网格Galerkin法的单位分解性质，通过在位移模式中嵌入不连续项表达由接触面引起的位移不连续和接触面端点的应力奇异，构造了不连续无网格位移场函数。然后结合摩擦接触定律的线性互补描述，给出一种新型的求解摩擦接触问题的无网格线性互补方法。几个数值算例验证了本文方法的可行性和有效性。岩石、混凝土等准脆性材料的破坏形式大多属于压剪性裂纹开裂破坏。这类破坏形式涉及接触非线性和裂纹断裂扩展两方面结合的问题，十分复杂，本文为无网格方法分析压剪性裂纹扩展问题提供了有力的支持，具有良好的应用前景。

[1]张雄, 刘岩, 马上. 无网格法的理论及应用[J]. 力学进展, 2009, 39(1): 1－36.ZHANG Xiong, LIU Yan, MA Shang. Meshfree methods and their applications[J]. Advances in Mechanics, 2009,39(1): 1－36.

[2]BELYTSCHKO T, FLEMING M. Smoothing, enrichment and contact in the element-free Galerkin method[J].Computers and Structures, 1999, 71: 173－195.

[3]庞作会, 葛修润, 王水林. 无网格伽辽金法(EFGM)模拟岩体不连续面[J]. 工程地质学报, 2000, 8(3):364－368.PANG Zuo-hui, GE Xiu-run, WANG Shui-lin. Simulation discontinuity with element-free Galerkin method(EFGM)[J]. Journal of Engineering Geology, 2000, 8(3):364－368.

[4]李卧东, 陈胜宏. 接触摩擦问题的数值模拟[J]. 岩土力学, 2003, 24(3): 385－388.LI Wo-dong, CHEN Shen-hong. Numerical modeling for frictional contact problems[J]. Rock and Soil Mechanics,2003, 24(3): 385－388.

[5]卢波, 丁秀丽, 邬爱清. 无网格法对岩体不连续面的模拟[J]. 岩石力学与工程学报, 2008, 27(10): 2108－2116.LU Bo, DING Xiu-li, WU Ai-qing. Modeling of rock discontinuity with meshless method[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(10):2108－2116.

[6]朱昌铭. 基于虚功原理的弹性接触问题的线性互补方法[J]. 力学学报, 1995, 27(2): 189－197.ZHU Chang-ming. A linear complementarity method for elastic contact problems based on the principle of virtual work[J]. Acta Mechanica Sinica, 1995, 27(2): 189－197.

[7]余天堂. 摩擦接触裂纹问题的扩展有限元法[J]. 工程力学, 2010, 27(4): 84－89.YU Tian-tang. An extended finite element method for modeling crack problems with frictional contact[J].Engineering Mechanics, 2010, 27(4): 84－89.

[8]BABUSKA T, MELENK J M. The partition of unity method[J]. International Journal for Numerical Method in Engineering, 1997, 40: 727－758.

[9]VENTURA A, XU J X, BELYTSCHKO T. A vector level set method and new discontinuity approximations for crack growth by EFG[J]. International Journal for Numerical Methods in Engineering, 2002, 54: 923－944.

[10]李世愚, 和泰名, 尹祥础. 岩石断裂力学导论[M]. 合肥: 中国科学技术大学出版社, 2010.

[11]LEI X. Contact friction analysis with a simple interface element[J]. Computer Methods in Applied Mechanics and Engineering, 2001, 190: 1955－1965.