应力腐蚀和压力溶解作用下双重孔隙岩体中THMM耦合过程的有限元分析

张玉军，杨朝帅

（1. 中国科学院武汉岩土力学研究所 岩土力学与工程国家重点实验室，武汉 430071；2. 中铁隧道集团有限公司 技术中心，河南 洛阳 471009）

1 引 言

当具有流体通道的孔隙和裂隙的双重岩体位于地下数千米的深度时，若在此处进行矿物和能源的回采、高放废物及CO2的隔离等人工活动，则环境应力和温度条件的改变可能影响这些通道的渗透特性。其综合效应对裂隙而言分别称之为应力腐蚀[1－4]和压力溶解[5－8]，前者引起支撑糙度的破裂（或压碎）、后者导致接触糙度溶解，从而使得裂隙产生闭合和其渗透性的退化。

这里的应力腐蚀，是指作用在裂隙支撑糙度上的压缩荷载引起局部拉应力时，将出现“次临界”或“准静态”的破裂,形成随时间发展的渐进破坏，特别是有水存在时由化学反应促使次临界裂纹的生长。而压力溶解则包括了3个连续的过程：首先在承受应力的接触糙度处矿物溶解；之后溶质沿着水膜扩散；最终在孔隙壁处溶质沉淀下来。

Dove[9]曾在较宽广的温度和 pH值范围内进行室内试验，以此严格地考察石英的溶解动力学，并得到了因化学溶解引起的I型裂纹扩展速率经验表达式。Yasuhara等[10]基于试验数据,考察一个含有单条天然裂隙的均密石英岩样中的裂隙开度的演化，由此提出描述该现象的应力腐蚀和压力溶解模型。Taron等[11]将压力溶解、热-水-应力收缩与膨胀、矿物沉淀与溶解对裂隙开度张开与闭合的复杂影响进行数学简化，建立了一种新的热-水-应力-化学双重介质模型，并以此结合TOUGHREACT和FLAC3D分析了天然裂隙岩体的渗透率变化机制。笔者等也曾对其所建立的双重孔隙—裂隙介质热—水—应力耦合有限元程序作了改进，即引入Ki-Bok Min等[12]提出的简化压力溶解模型，对裂隙开度进行适时修正，建立裂隙的渗透系数随压力溶解的演化模式，并以一个假定的位于非饱和地层中的高放废物地质处置库为算例，针对3种裂隙开度的工况开展了数值模拟[13]。然而这其中并没有考虑溶质浓度场。众所周知，高放废物地质处置中核素可能的泄漏与扩散是非常重要的研究内容[14]，故基于上述工作，完善已有的计算模型和有限元程序，进行热-水-应力-迁移耦合分析势在必行。

为此笔者首先在文献[13]的控制方程中引入Yasuhara的应力腐蚀和压力溶解模型，再加进溶质浓度场，即对于孔隙-裂隙双重介质，认为应力场和温度场是单一的，但存在着孔隙水压力和裂隙水压力、孔隙浓度和裂隙浓度，从而可模拟相应的热-水-应力-迁移耦合过程。然后针对一个假定位于非饱和双重孔隙-裂隙介质中的高放废物地质处置库，拟定2种工况：（1）裂隙开度随应力腐蚀和压力溶解而变化（基岩的孔隙率亦是应力的函数）；（2）裂隙开度和基岩的孔隙率均为常数，在一定的初始温度、孔隙水压力、岩体应力和核素释放强度条件下，进行有限元分析，考察了处置库近场的温度、孔隙水压力、水流速、饱和度、核素浓度和应力的分布与变化，得出了若干有意义的认识。

2 裂隙渗透特性的修正

2.1 应力腐蚀对裂隙开度的影响

如图1所示，假定脆性材料的裂隙中粗糙面接触是Hertzian接触，则在这种接触的内部或外部可能因拉应力σt产生圆形裂纹，此被称为应力腐蚀。Dove[9]对石英材料定义其中I型裂纹的扩展速率为

式中：r为沿由σt产生的I型裂纹长轴方向的距离，假定裂纹的初始长度及r都是足够小的；μ为材料的泊松比；σt为由σa引起的拉应力，其在裂隙的接触边缘达到最大值；σa为作用在裂隙接触面积上的真实压应力；为裂隙的名义面积（可取单位值）；Rc是裂隙的接触面积，并且

Rc由下式求算：

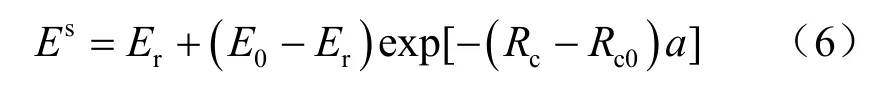
式中：E、Er和E0依次为裂隙力学开度的平均值、残余值和初始值；Rc0为裂隙接触面积的初始值；a为经验常数。

从而裂隙力学开度因应力腐蚀的演化律为

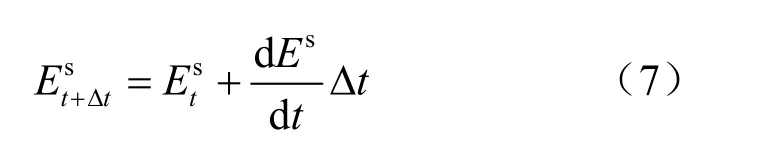
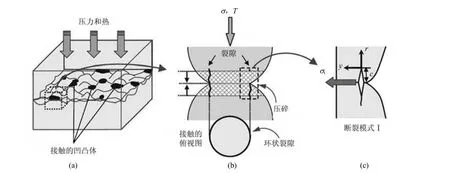
图1 微裂纹传播引起的裂隙压缩[10]Fig.1 Schematic of fracture compaction induced by miscrocrack propagation[10]

2.2 压力溶解对裂隙开度的影响

Yasuhara等[10]定义了物质的溶解速率为

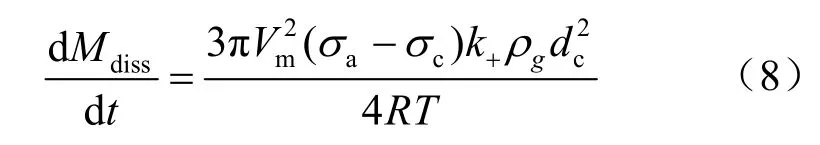
式中：d Mdiss/dt为从裂隙界面上进入溶液中的溶解质量速率；Vm为固体的摩尔体积；σc为临界应力，当时体系达到平衡、反应停止；k+为固体的溶解速率常数；ρg为固体的密度；dc为粗糙面接触的直径。

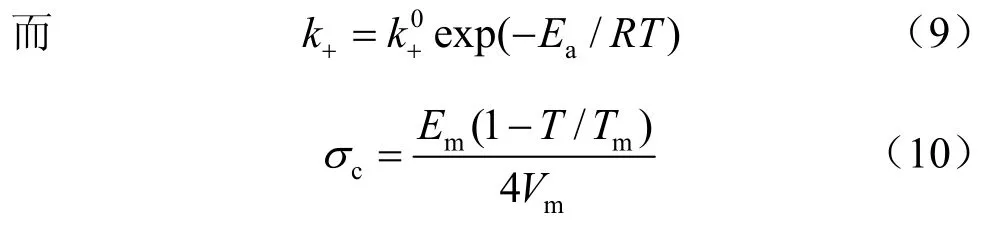
则裂隙力学开度的压力溶解闭合速率为

从而裂隙力学开度因压力溶解的演化律亦为

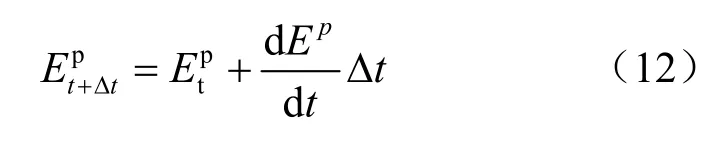
2.3 裂隙渗透系数

设岩体中裂隙的间距为s，而单条裂隙开度为

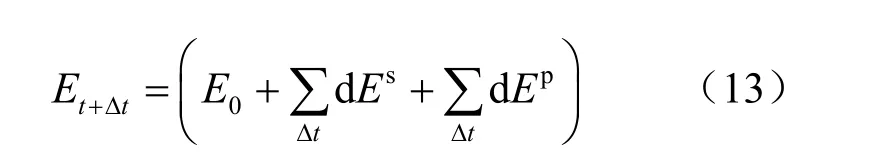
故单条裂隙的水力开度为[15]

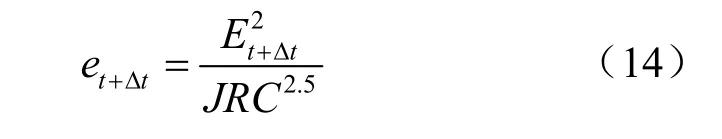
式中：JRC为裂隙粗糙度系数。

从而，等效后裂隙岩体的渗透系数为

式中：g为重力加速度（ 9.81 m/s2）；ν为运动黏度（对于20℃的纯水其值为 1.0× 10-6m2/s ）。

2.4 应力对基岩渗透系数的影响

而对于基岩的孔隙率和渗透系数，当岩体中的应力发生改变时，可根据Davis等[16]提出经验公式进行如下修正

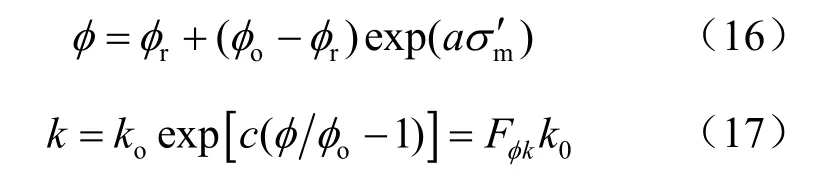
式中：φo、ko分别为0应力状态的基岩孔隙率和渗透系数；φr为高应力状态下的基岩残余孔隙率；σm′为平均有效应力；a、c分别是由试验确定的参数；Fφk为孔隙渗透系数的修正因子。

3 渗透-迁移方程引入

笔者对于参考文献[17]中渗透-迁移方程进行了改进,其新意在于增加了孔隙岩体和裂隙介质之间因浓度差产生的溶质交换，其形式如下：

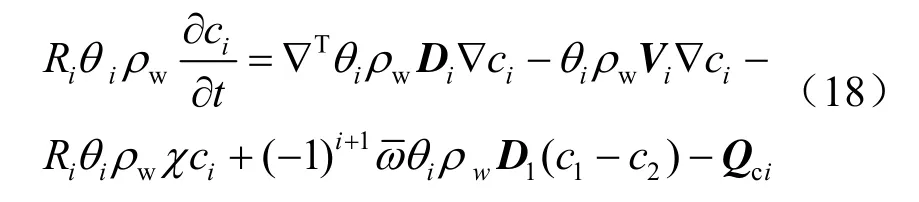
而扩散张量可表示为

式中：αiT为横向弥散度；αiL为纵向弥散度；为表观流速的绝对值；αim为分子扩散系数；τi为曲折率；δαβ为克罗内克符号。

笔者将Yasuhara的应力腐蚀和压力溶解模型以及式（18）引入已有的双重孔隙-裂隙岩体热-水-应力耦合控制方程[13]中,其有限元算法可见文献[18]。

4 算 例

如图2所示，在地下深处埋入一个圆柱状核废料玻璃固化体，其周围是非饱和的双重孔隙-裂隙石英岩体。将该模型近似简化为平面应变问 题。取计算域尺寸水平向为4 m，垂直向为8 m，有800个单元，861个节点。从固化体边缘向右的点号依次为 432、433、434、435、436。其边界条件为：顶面位移自由，其上作用有分布荷载σv= 26.7 MPa；左、右侧面的水平方向位移约束；底面的垂直方向位移约束；所有边界的孔隙水压力为 -4.59 MPa、裂隙水压力-0.46 MPa及温度20 °C固定。岩体中发育有水平及垂直两组裂隙，热-水-应力耦合的环境对裂隙的开度要产生应力腐蚀和压力溶解作用。有关的计算参数见表1～3（表3中除Rc0、和JRC外，其余参数取自文献[10]）。初始状态时，岩体的温度均为20 °C。核废物以1 000 W的不变功率释放热量，时间经历了4 a。

孔隙介质和裂隙介质的水分特性曲线符合 Van Genuchten模型，即

式中：对于孔隙介质，α = 3.86× 10-6m-1，n=1.41；对于裂隙介质，α = 5.26× 10-4m-1，n=2.55；m=1-1/n；ψ为水势；sws为最大饱和度，其值为1.0；swr为最小饱和度，对孔隙介质和裂隙介质其值各取0.19和0.01。

比渗透率与饱和度的关系为

取孔隙介质及裂隙介质的温度梯度水分扩散系数相同，即 Dt= 2.5× 10-10m2/s ℃

贮存罐为孔隙岩体中的源项，某种放射性核素的释放强度为 Qc=1.44× 10-10mol⋅kg/m3⋅s-1。设与核素的渗透迁移有关且在计算中不变的参数为：孔隙曲折率τ1、τ2分别为0.4、0.8，纵向弥散度α1L、α2L分别为1.0 m和2.0 m，横向弥散度αiT=αiL/10，分子扩散系数α1m、α2m分别为 1.0×10-9m2/s和2.0×10-9m2/s，分配系数Kd1、Kd2分别为8.0 ml/g和 5.3 ml/g，干密度ρd1、ρd2分别为 2.3 g/m3和2.1 g/m3，参数为100.0 m-2，放射性核素的衰减常数χ= ln2/Thalf，其中Thalf为半衰期，取为1 000 a。

针对前述的2种裂隙开度变化工况，计算了岩体中的温度、位移、孔隙水压力、核素浓度和应力等的变化及分布情况，其主要结果及分析如下。

图2 计算模型Fig.2 Computation model

工况1和工况2两种条件下计算域中的温度变化基本相同。以工况1为例，432、433、434、435各点处的温度随时间的变化曲线见图3。由图看到，在开始的约0.1 a内缓冲层的温度快速上升，之后增加减缓，到计算终了时432、433、434、435各点的温度依次为 77.8 °C、62.0 °C、52.5 °C 和 45.7 °C。

图3 工况1温度-时间曲线Fig.3 Temperatures versus time at some nodes for case 1

图4、5分别为玻璃固化体右缘中点的水平和垂直裂隙开度因应力腐蚀、压力溶解产生的闭合速率随时间的变化。从中看到，两种因素产生的闭合速率均先随时间增加，到达峰值再衰减，之后逐渐趋于不变，并且应力腐蚀引起的闭合速率要比压力溶解引起的闭合速率高 6个数量级，这与文献[10]中呈现的规律类似；同时水平裂隙开度比垂直裂隙开度闭合速率大，这是由于岩体中垂直应力大于水平应力的缘故。

图4 玻璃固化体右缘中点因应力腐蚀引起的-时间曲线Fig.4 caused by stress corrosion versus time at middle point of right margin of vitrified waste

图5 玻璃固化体右缘中点因压力溶解引起的-时间曲线Fig.5 caused by pressure solution versus time at middle point of right margin of vitrified waste

图6、7分别表现了该中点处水平和垂直裂隙开度、粗糙面接触率随时间的演化，前者由初始开度下降而趋于残余开度，后者由初始接触率上升而趋于其名义接触率（单位值），并且对应于水平裂隙的值的变化明显要快。

图6 玻璃固化体右缘中点裂隙开度-时间曲线Fig.6 Fracture apertures versus time at middle point of right margin of vitrified waste

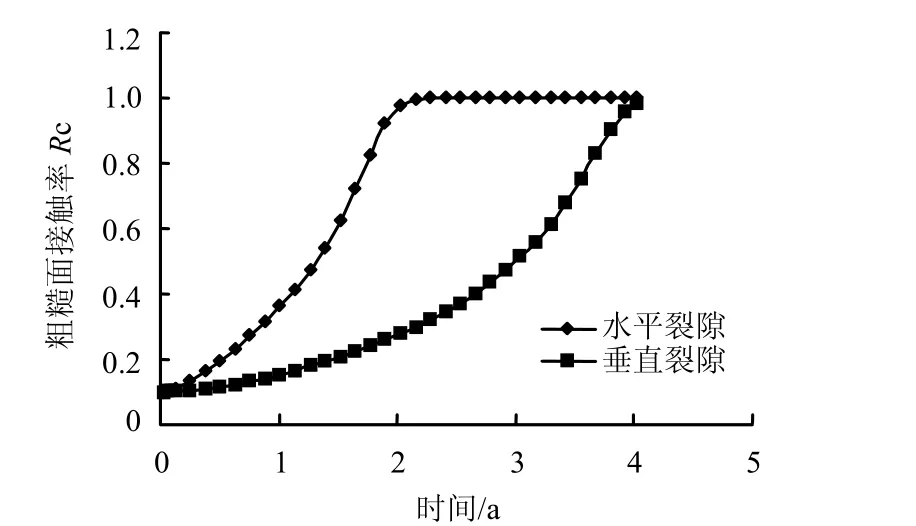
图7 玻璃固化体右缘中点粗糙面接触率-时间曲线Fig.7 Contact-area ratios versus time at middle point of right margin of vitrified waste

从图8看到，在该中点处水平裂纹上的应力强度因子比垂直裂纹上的应力强度因子大得多，且二者均随时间减小。

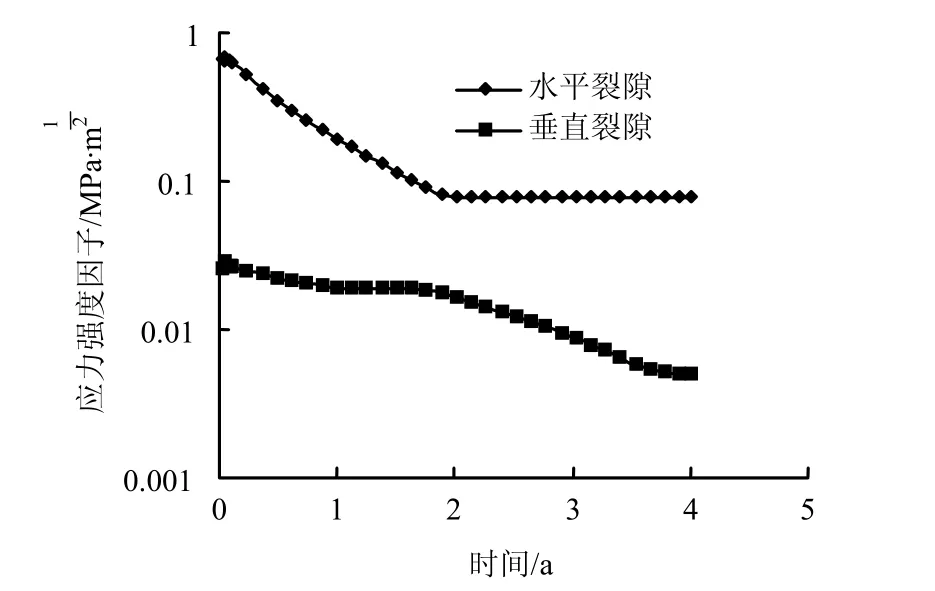
图8 玻璃固化体右缘中点应力强度因子-时间曲线Fig.8 Stress intensity factors versus time at middle point of right margin of vitrified waste

而图9显示了该中点处水平和垂直裂隙的临界应力相同，且其在开始阶段快速下降，之后逐渐趋于常数。产生上述现象的原因正是由温度、应力与化学的综合作用。

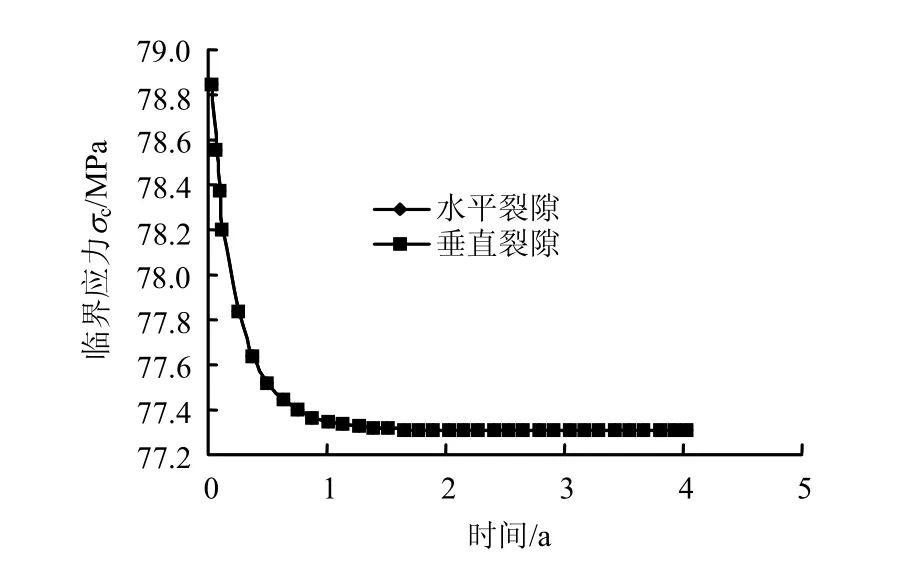
图9 玻璃固化体右缘中点临界应力-时间曲线Fig.9 Critical stresses versus time at middle point of right margin of vitrified waste

图10、11为工况1、2中432、433、434、435各点处的孔（裂）隙水压力随时间的变化曲线。比较后看到，由于工况1考虑了应力腐蚀和压力溶解对裂隙开度的减小作用及孔隙的渗透系数随应力的变化，而工况2的裂隙开度及孔隙的渗透系数保持为常数，故工况1的负孔（裂）隙水压力上升较高，特别是在应力腐蚀和压力溶解效应最强烈的 432点，该处的负裂隙水压力达到很大的值。在4 a时432点的负孔（裂）隙水压力分别为工况1：-12.25、-7.95 MPa；工况 2：-6.03、-0.66 MPa。

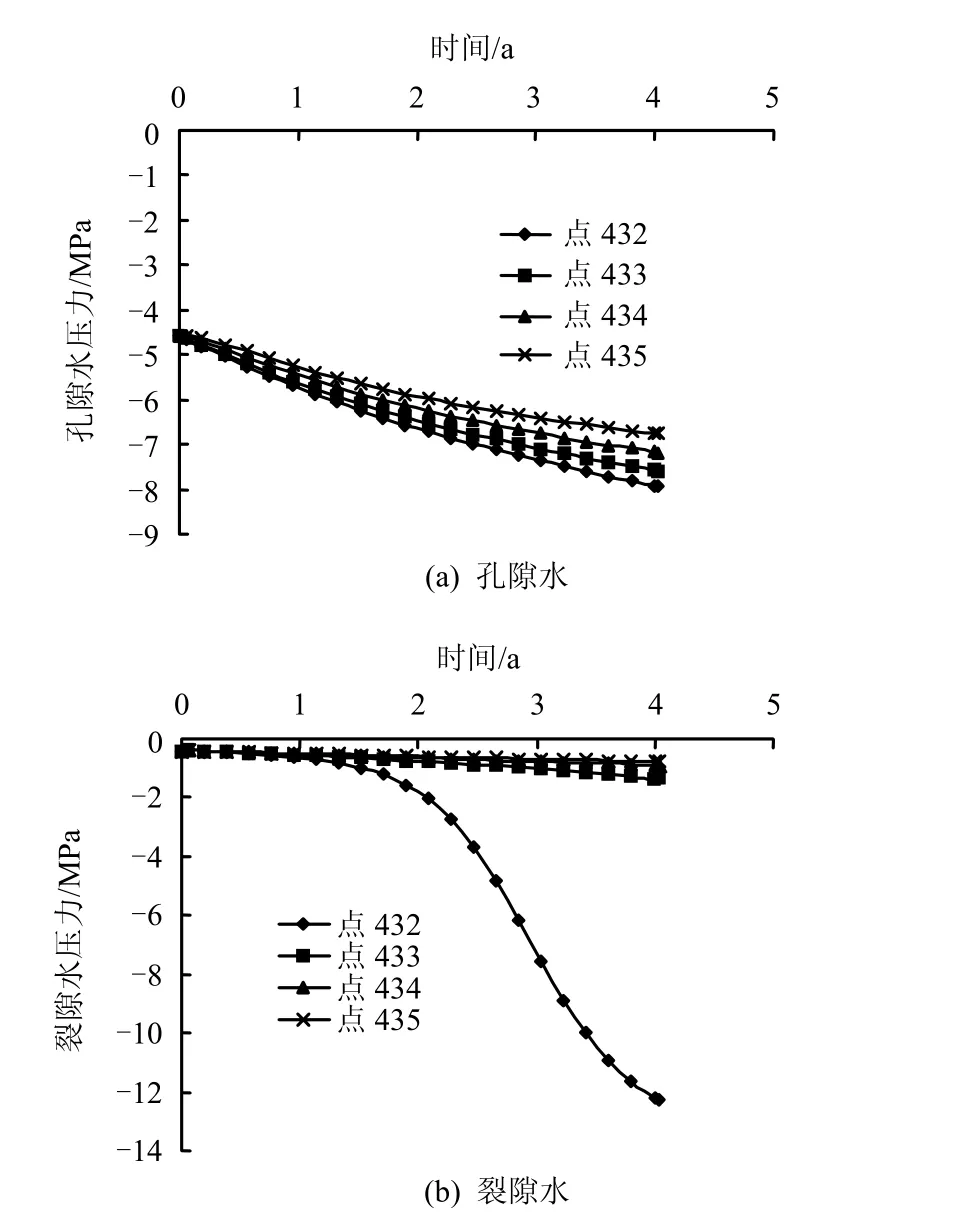
图10 工况1孔(裂)隙水压力-时间曲线Fig.10 Pore and fracture water pressures versus time at some nodes for case 1

图11 工况2孔(裂)隙水压力-时间曲线Fig.11 Pore and fracture water pressures versus time at some nodes for case 2

图12、13是工况1、2在4 a时贮存罐周围2 m×2 m范围内孔（裂）隙水压力等值线的分布。从中看到，由于工况1受到应力腐蚀和压力溶解的影响，与工况2相比，其中的裂隙水压力在贮存罐周围呈现明显的增高区域。

图14为两种工况在4 a时计算域中的孔隙水流速和裂隙水流速矢量分布。可以看到，由于工况 1考虑了应力腐蚀和压力溶解效应，与工况2相比，其中的裂隙水流速矢量有显著的不同，特别是在贮存罐附近。以432点为例，孔隙水流速和裂隙水流速分别为工况1： 3.40 × 10-8、1 .52× 10-8m/s ；工况2： 2.32× 10-8， 2.77× 10-8m/s 。

图15、16是2种工况中432、433、434、435各点处的孔隙核素浓度和裂隙核素浓度随时间的变化曲线。比较后可知，由于工况1中考虑了应力腐蚀和压力溶解对裂隙开度的减小作用、平均有效应力对孔隙率的压缩功能，使得裂隙和孔隙的渗透系数降低，而工况2中的裂隙开度、孔隙率及其渗透系数均为常数，故工况1的裂隙和孔隙中核素聚集程度较高，到4 a时2种工况中432、433、434、435各点的核素浓度分别为孔隙岩体：20.18/6.82、15.42/3.60、12.06/2.55、9.36/1.76；裂隙介质：0.86/18.44、8.39/6.82、6.28/5.54、5.00/4.63（“/”的上、下分别是工况1、2的数据，其单位是 10-3mol/m3）。

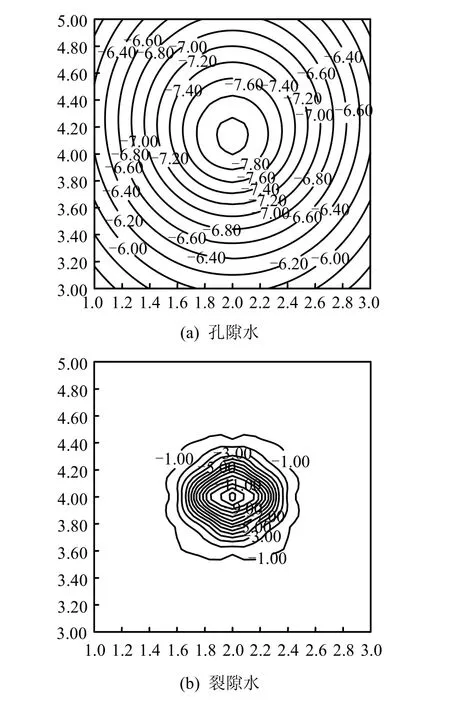
图12 工况1中4 a时2 m×2 m区域中的孔(裂)隙水压力等值线(MPa)Fig.12 Contours of pore and fracture pressures in a 2 m×2 m area at 4 years for case 1 (MPa)

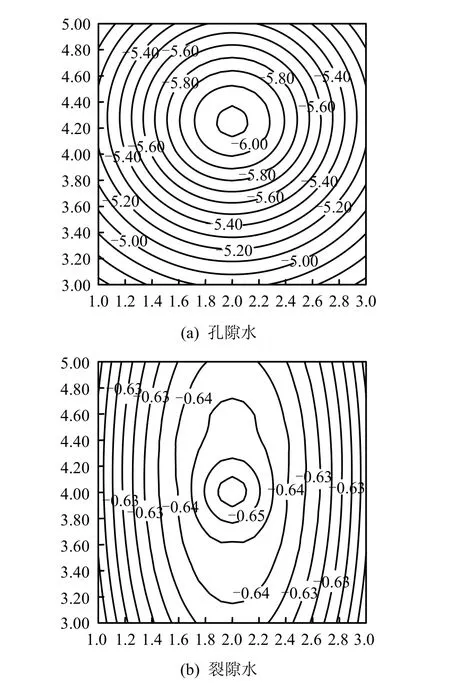
图13 工况2中4 a时2 m×2 m区域中的孔(裂)隙水压力等值线(MPa)Fig.13 Contours of pore and fracture pressures in a 2 m×2 m area at 4 years for case 2 (MPa)

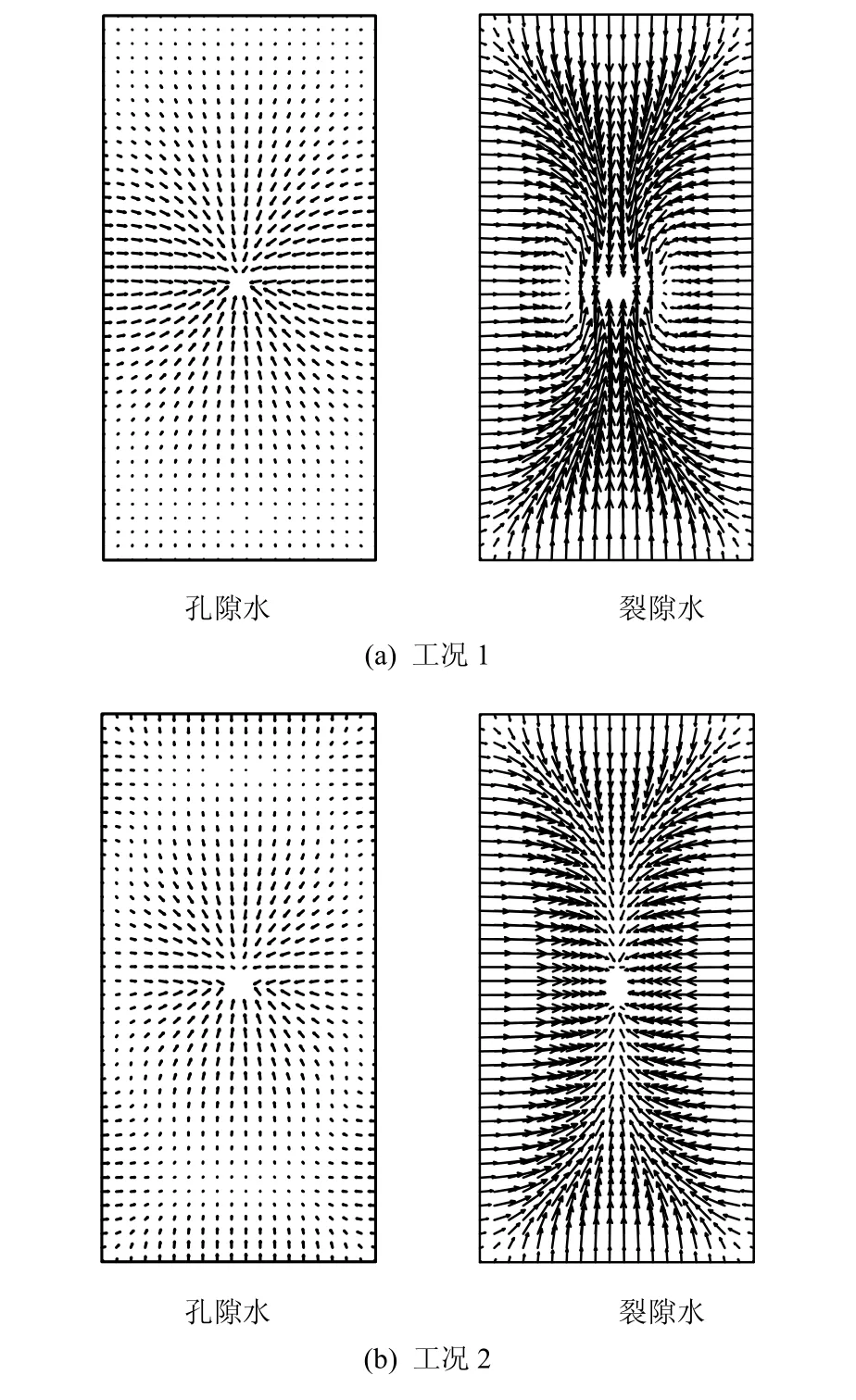
图14 4 a时计算域中的孔(裂)隙水流速矢量Fig.14 Flow vectors of pore and fracture water in calculation domain at 4 years

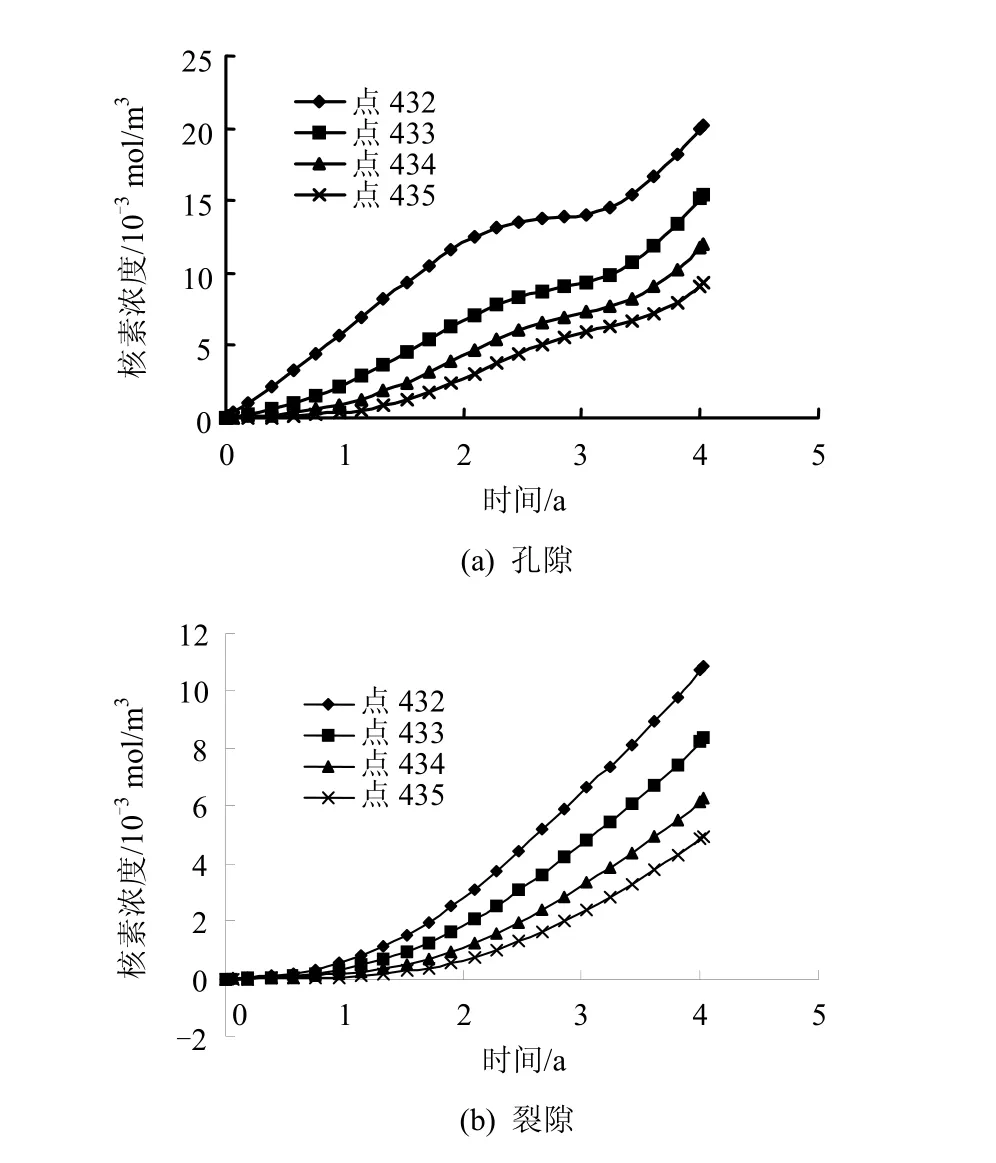
图15 工况1中4 a 时岩体中核素浓度-时间曲线Fig.15 Nuclide concentrations versus time at some nodes for case 1

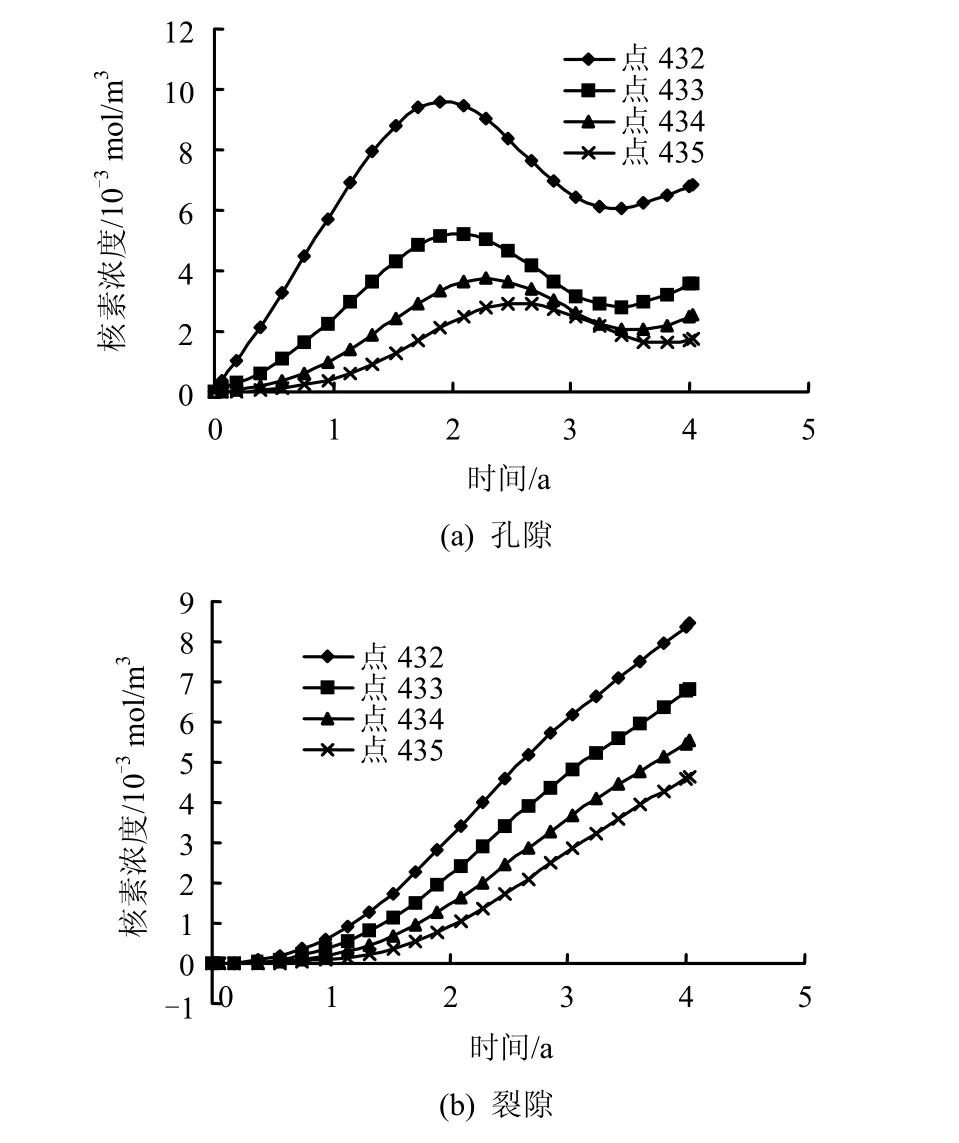
图16 工况2中4 a时岩体中核素浓度-时间曲线Fig.16 Nuclide concentrations versus time at some nodes for case 2

图17、18是2种工况4 a时贮存罐周围2 m×2 m范围内的核素浓度和裂隙核素浓度等值线分布。

图17 工况1中4 a时2 m×2 m区域中核素浓度等值线(10-3 mol/m3)Fig.17 Contours of nuclide concentration in a 2 m×2 m area at 4 years for case 1 (10-3 mol/m3)

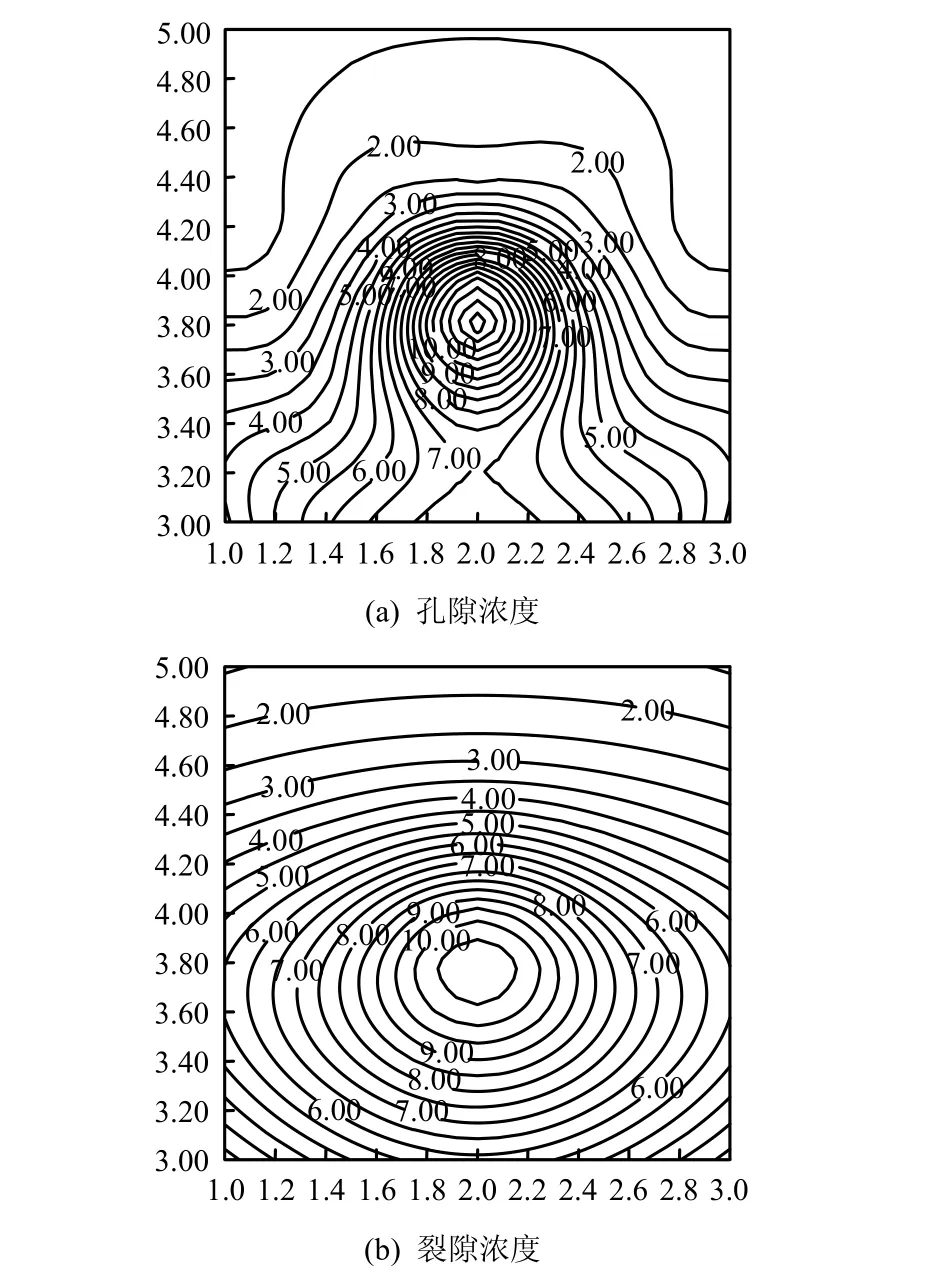
图18 工况2中4 a时2 m×2 m区域中核素浓度等值线(10-3 mol/m3)Fig.18 Contours of nuclide concentration in a 2m×2m area at 4 years for case 2 (10-3 mol/m3)

由于不考虑负的孔（裂）隙水压力对应力平衡的影响[19]，两种工况的计算域中应力量值及分布差别很小，这里以工况1为例给出4 a时计算域中的正应力等值线，见图19。从中看到，由于玻璃固化体的存在及放热效应，使得计算域中的应力场不同于仅由岩体自重产生的应力场（后者的应力等值线为水平线）。到4 a时玻璃固化体右缘中点的水平应力和垂直应力分别为-0.124 MPa和-26.75 MPa。

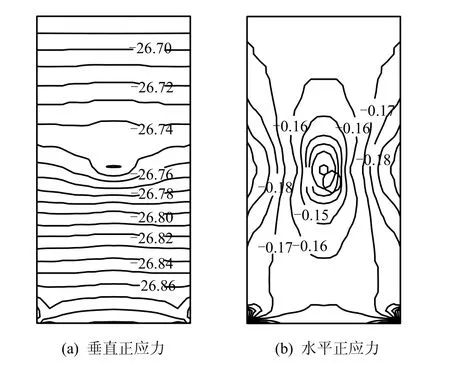
图19 4 a时工况1计算域中正应力等值线(MPa)Fig.19 Normal stress contours in calculation domain at 4 years for case 1 (MPa)

表1 主要计算参数Table 1 Main computational parameters

表2 裂隙组的计算参数Table 2 Parameters for fracture sets used in calculation

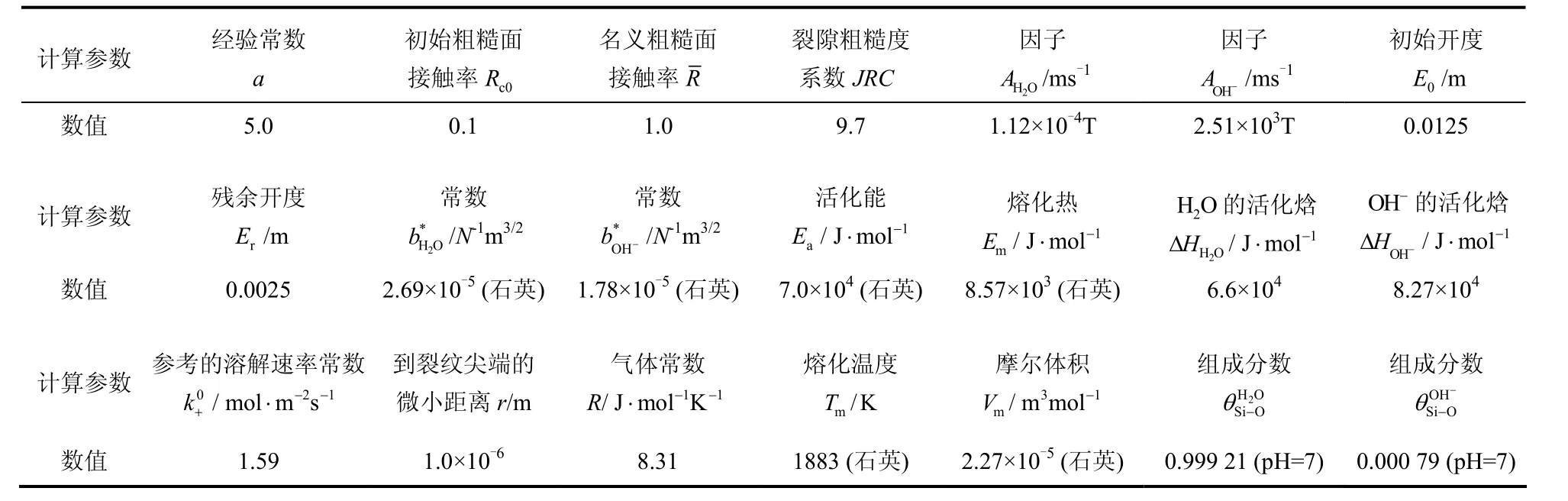
表3 应力腐蚀和压力溶解的计算参数Table 3 Parameters for stress corrosion and pressure solution

5 结 论

针对已建立的双重孔隙-裂隙介质热-水-应力耦合控制方程，在应用了Yasuhara等提出的裂隙开度的应力腐蚀和压力溶解算式的基础上，引入溶质浓度场，发展为相应的热-水-应力-迁移耦合模型。以一个假定的位于非饱和双重孔隙-裂隙岩体中的高放废物地质处置库的核素泄漏为算例，就主要考虑裂隙开度是否随应力腐蚀和压力溶解而变化（同时基岩的孔隙率也作为是否是应力函数的处理）的2种工况，通过热-水-应力-迁移耦合的二维有限元模拟，考察了岩体中的温度、裂隙开度的闭合速率、闭合量、孔隙水压力、地下水流速、核素浓度和正应力的变化、分布情况。计算结果表明：工况1、2中的温度状态差别不大,计算终了（4 a）时，近场的温度可达到 30.0 °C～80.0 °C；应力腐蚀引起的闭合速率要高于压力溶解引起的闭合速率6个数量级，且两种因素产生的闭合速率随时间先增加后减小，并趋于稳定；随着时间的推移裂隙开度由初始值下降并趋于残余值，而粗糙面接触率亦由初始值上升并趋于其名义值；作用在裂纹上的应力强度因子及临界应力均随时间减小，并趋于常数；当考虑应力腐蚀和压力溶解时，与不计该作用时相比，近场的负裂隙水压力上升很高，且其流速矢量场有显著的不同；由于工况1中应力腐蚀、压力溶解和平均有效应力使得裂隙和孔隙的渗透系数降低，而工况 2中的裂隙及孔隙的渗透系数均为常数，故前者的裂隙和孔隙中核素浓度较后者为高；但2种工况的岩体中的应力量值及分布基本相同。

[1]ATKINSON K. A fracture mechanics study of subcritical tensile cracking of quartz in wet environments[J]. Pure and Appl. Phys., 1979, 117: 1011－1024.

[2]DOVE M. The dissolution kinetics of quartz in sodium chloride solutions at 25° to 300°C[J]. Am. J. Sci., 1994,294: 665－712.

[3]CHESTER S, LENZ C, CHESTER M, et al. Mechanisms of compaction of quartz sand at diagenetic conditions[J].Earth Planet Sci. Lett., 2004, 220(3－4): 435－451.

[4]NARA Y, KANEKO K. Study of subcritical crack growth in andesite using the double torsion test[J]. Int. J. Rock.Mech. Min. Sci., 2005,42(4): 521－530.

[5]ROBIN F. Pressure solution at grain to grain contacts[J].Geochim. Cosmochim. Acta, 1978, 42: 1383－1389.

[6]DEWERS T, HAJASH A. Rate laws for water-assisted compaction and stress-induced water-rock interaction in sandstones[J]. J. Geophys. Res., 1995, 100: 13093－13112.

[7]REVIL A. Pervasive pressure-solution transfer: A poro-visco-plastic model[J]. Geophys. Res. Let., 1999,26: 255－258.

[8]YASUHARA H, ELSWORTH D, POLAK A. Evolution of permeability in a natural fracture: Significant role of pressure solution[J]. J. Geophys. Res., 2004, 109(B3):B03204. doi: 10.1029/2003JB002663.

[9]DOVE M. Geochemical controls on the kinetics of quartz fracture at subcritical tensile stresses[J]. J. Geophys. Res.,1995, 100(B11): 22349–22359.

[10]YASUHARA H, ELSWORTH D. Compaction of a rock fracture moderated by competing roles of stress corrosion and pressure solution[J]. Pure. Appl. Geophys., 2008,165: 1289－1306.

[11]TARON J, ELSWORTH D. Thermal-hydrologicmechanical-chemical processes in the evolution of engineered geothermal reservoirs[J]. Int. J. Rock. Mech.Min. Sci., International Journal of Rock Mechanics and Mining Sciences, 2009, 01: j.ijrmms. doi: 07. 1016/200901.

[12]MIN K B, RUTQVIST J, ELSWORTH D. Chemical and mechanically mediated influences on the transport and mechanical characteristics of rock fractures[J].International Journal of Rock Mechanics and Mining Sciences, 2009, 02: j.ijrmms. doi: 10. 1016/200804002.

[13]张玉军, 张维庆. 裂隙开度的压力溶解对双重孔隙介质热-水-应力耦合影响的有限元分析[J]. 岩土力学,2010, 31(41): 1269－1275.ZHANG Yu-jun, ZHANG Wei-qing. Finite element analysis of influence of pressure solution of fracture aperture on T-H-M coupling in dual-porosity medium[J].Rock and Soil Mechanics, 2010, 31(41): 1269－1275.

[14]SONNENTHAL E, ITO A, SPYCHER N, et al.Approaches to modeling coupled thermal, hydrological,and chemical porcesses in the drift scale heater test at Yucca Mountain[J]. International Journal of Rock Mechanics and Mining Sciences, 2005. 42(5/6), 698－719.

[15]OLSSON R, BARTON N. An improved model for hydromechanical coupling during shearing of rock joints[J]. International Journal of Rock Mechanics and Mining Sciences, 2001, 38(3): 317－329.

[16]DAVIS J, DAVIS D. Stress-dependent permeability:Characterization and modeling[R]. [S.l.]: Society of Petroleum Engineers, 1999.

[17]NISHIGAKI M. Density dependent transport analysis saturated-unsaturated porous media—3 dimensional eulerian lagrangian method[R]. [S.l.]: Okayama University, 2001.

[18]张玉军, 张维庆. 双重孔隙介质 THMM 耦合模型及其有限元分析[J]. 力学学报, 2010, 42(4): 660－669.ZHANG Yu-jun, ZHANG Wei-qing. Coupled thermohydro-mechanical-migratory model and FEM analyses for dual-porosity medium[J]. Chinese Journal of Theoretical and Applied Mechanics, 2010, 42(4): 660－669.

[19]CHIJIMATSU M, KURIKAMI H, ITO A, et al.Implication of THM coupling on the near-field of a nuclear waste repository in a homogeneous rock mass[M].[S.l.]: [s.n.], 2002.