鱼雷射击随机误差分析的几个问题

李长文, 任行者, 王 鹏



鱼雷射击随机误差分析的几个问题

李长文, 任行者, 王 鹏

(海军潜艇学院科研部软件中心, 山东青岛, 266071)

借助直航鱼雷直进射击的描述, 研究了射击命中问题的随机误差及其相关性的概念, 指出了基于目标运动要素观测值或真值计算成功概率的不同。就客观概率情形, 基于误差向量函数的1阶近似或2阶近似研究了计算概率的解析方法, 以及关于正态随机向量的一般二次函数分布的均值、方差和特征函数计算公式的一个定理, 给出了2阶近似情形计算概率的解析方法, 数值实验发现, 就直航鱼雷直进射击成功的客观概率而言, 两种方法均有较高精度, 且1阶近似方法优于2阶近似方法。

直航鱼雷; 随机误差; 客观概率; 解析方法

0 引言

直航、声自导、尾流自导鱼雷射击的目的通常是为了满足无误差假设下的命中或自导发现目标的条件, 当目标运动要素观测值相对实际值或鱼雷运动参数实际值相对设定值有观测误差时, 在假设这些误差为随机误差的条件下, 将面对一系列问题, 以往的研究一般关注命中或发现概率的计算, 对误差的选取及假设有一定随意性, 且不区分基于观测值与真值所计算概率的不同, 计算的方法一般以仿真为主, 有些解析方法精度不足, 未见关于用解析方法进行较精确的快速计算的相关研究。事实上, 鱼雷射击的随机误差分析将涉及随机误差源、误差的相关性、命中或自导发现目标的主观或客观概率、计算概率的仿真与解析方法等几个问题, 本文试图对这些问题进行系统讨论, 为简单起见, 以直航鱼雷直进射击为例, 这些论述同样适用于声自导或尾流自导鱼雷转角射击, 只是其数学描述相对复杂, 本文只为说明一些概念与方法, 实际应用时还有待于做进一步深入研究。

1 直进射击的随机误差源

假设潜艇用直航鱼雷以直进射击方式攻击等速直航目标, 目标位置点与瞄准点相同, 位于长度L的目标舰船的中点处, 目标运动要素观测值以当前时刻相对态势 (,,)或绝对态势 (,,,) 描述, 其中为目标距离,为目标速率,为目标舷角,为目标航向,为目标方位, 下面的计算公式中用标准单位。

无误差条件下鱼雷发射后以设定速率V匀速直线运动, 且鱼雷与目标的运动可以看成同一水平面上的运动, 攻击决策者以发射鱼雷时刻的运动要素观测值(,,)及V计算射击参数直进射击的提前角

= arcsin(sin) (1)

式中,=/V为目标速率与鱼雷速率之比, 不考虑误差的作用, 以提前角发射的鱼雷将与瞄准点相遇, 这个提前角存在的条件为 (< 1)或(= 1, ||

1, ||≤arcsin(1/)], 其中最后一个条件对应两个提前角, 上述公式计算的是使鱼雷与目标相遇时间较小的一个。另一个提前角为p–arcsin(sin), 在鱼雷速度实际上大于目标速度的条件下, 可不考虑上述计算提前角的定义域, 以下只讨论这一情形, 即假设< 1。

设目标运动要素有观测误差, 观测值(,,,)与其对应的真值(,,,)之差为(D,D,D,D), 即=+D,=+D,=+D,=+D, 则目标舷角观测值为=(+p–), 真值为=(+p–),()表示将变为(–p,p)上与终边相同角的函数, 假设误差不改变目标舷别, 则目标舷角观测误差为

D=–=D–D(2)

可见目标舷角误差是方位误差及航向误差的函数, 计算概率时不便将其作为一个独立误差项。

因为目标运动要素观测值一般由目标运动要素解算过程给出, 对于纯方位情形当前时刻的目标运动要素由初始时刻的目标运动要素、解算时间、观测站在解算过程中的机动状态决定, 发射鱼雷时刻目标运动要素观测误差向量(D,D,D)或(D,D,D,D)的统计规律可以用重复试验的方式进行研究, 这个统计规律可以用(D,D,D,D)的联合概率分布表示。数值实验发现, 纯方位方法给出的目标运动要素观测误差各分量D,D,D,D不是相互独立的, 因此, 在研究鱼雷攻击成功概率这类问题时, 忽略目标运动要素解算过程, 而从直接假设目标运动要素观测误差为相互独立的零均值正态随机误差开始, 这一做法与实际不符。后面还将说明, 即使接受发射鱼雷时刻目标运动要素观测误差为相互独立的这一前提, 以(D,D,D)而不是以(D,D,D,D)表达这些误差是不合理的。

设鱼雷实际速率为V, 实际速率相对设定速率的误差记为DV=V–V,DV的统计规律可以用给定设定值V条件下的重复试验进行研究, 研究结果是客观的, 假设为DV~(0,),为已知常数。

鱼雷计划航向设定的基准为发射鱼雷时刻观测的目标方位线, 这个航向为C=+, 鱼雷按计划航向发射后, 其运动过程除速率误差外, 还有鱼雷航向误差, 设为DC,DC作为实际航向与设定航向之差, 其统计规律可以用重复试验的方法进行研究, 研究的结果是客观的, 假设为DC~(0,),为已知常数。

鱼雷实际航向为C=++DC, 鱼雷实际航向相对发射鱼雷时刻目标实际方位的角=C–=–DC+D, 实际提前角误差

D=–=D–DC(3)

从式(2)、式(3)可以看出,D与D关于D正相关。虽然可以用(,,) 表示发射鱼雷时刻的相对态势, 但以往只用(D,D,D) 表示发射态势的观测误差, 进而假设提前角误差就是鱼雷航向误差DC, 且与这些误差相互独立, 与实际不符。正是出于这一考虑, 目标运动要素误差应以(D,D,D,D)表示, 直航鱼雷直进射击的随机误差源可选为 (D,D,D,D,DV,DC)。

2 鱼雷命中目标的条件及概率

以发射鱼雷时刻目标实际位置点为坐标原点, 目标运动方向为轴正方向,轴向右旋转90°的方向为轴正方向建立一个直角坐标系, 以发射鱼雷时刻为0时刻,时刻鱼雷位置点对应的复数记为(), 则

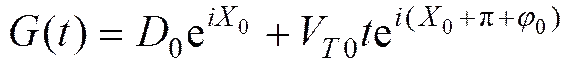
不考虑航程的限制, 令() 的虚部为0, 可得鱼雷到达目标航线的时刻, 进一步计算这一时刻目标到鱼雷的有向线段的数量

x=(5)

鱼雷命中目标的条件

Con =xÎ[ –L/ 2,L/ 2 ] (6)

Con 取值1 (表示命中)或0(表示不命中)。

对于决策现场之外能控制(,,)以及V取值的人, (,,)和V可以看成是已知的, 假设鱼雷攻击的决策者总是在一定时间利用目标运动要素观测值计算射击参数并发射鱼雷, 则x可表示为(,,,V,D,D,D,DV,DC)的函数, 其中(D,D,D,DV,DC) 为统计规律已知的随机误差向量, 因此Con为统计规律确定的0~1两点分布的随机变量, 这时可以用=con表达攻击成功的可能性, 即成功的概率, 其作用为在观测到攻击结果之前, 对攻击成功的可能性预先进行的度量。这个概率可以用给定(,,,V)条件下的重复试验进行验证, 是客观的, 可以用于特定假设条件下作战效能的评估, 但不能直接用于攻击决策的支持。计算客观概率时, 观测值是目标运动要素真值及随机误差的函数, 因为射击参数是观测值及设定值的函数, 所以仿真计算时需重复计算。

鱼雷攻击的现场决策者, 一般不知(,,)而只知(,,) 及V, 这时只能将x表示为(,,,V,,,,D,D,D,DV,DC)的函数, 其中(D,DV,DC)为统计规律已知的随机误差向量, (,,)是客观存在但未知的常数, 关键是(,,)的取值是判定Con所必需的, 这时Con是一个含有随机成分的不确定问题。

以往的做法是, 利用=–D,=–D,=– (D–D), 而(D,D,D,D,DV,DC)的统计规律是已知的, 则认为,,是统计规律已知的随机变量, 并且在仿真计算时用相应分布的伪随机应变数代替这些随机误差, 而用观测值与这些伪随机数之差(对于零均值正态情形, 之和亦无所谓)表示真值, 就可以计算所谓的概率。这一做法的不当之处为关于目标运动要素误差的统计规律, 以目标速率误差为例, 当说D=–~(0,)这类结论时, 其实质是固定, 进行相同条件下的重复试验, 则观测值表现出以为均值的正态分布统计规律。这一实质不能改写为当已知一次观测值时, 真值是一个随机变量, 且服从以这个观测值为均值的正态分布, 均方差为。究其原因, 首先, 将真值作为一个随机变量只是一种观点, 并不符合实际; 其次, 即使认为真值是随机变量, 由于观测值的不可控制性, 几乎不可能进行相同观测值条件下关于真值的重复试验, 即几乎总是面对只有一个样本的问题, 想象的~(,) 是无法验证的。

就这类现象, 针对目标速率真值未知而又需要的问题, 统计学上的Bayes 学派所采取的是如下一系列观点和做法: 1) 将其当作不确定性问题, 无论其是否具有严格意义下的统计规律, 主观上通过假设真值为随机变量描述这个不确定性; 2) (,)是一个2D随机向量,(,)将被看成是关于的条件分布; 3) (,)的联合分布是未知的, 然而关于目标速率真值总应有些先验知识, 只要用概率分布密度函数表达这些知识, 就可以给出(,) 的联合分布密度; 4) 利用的一次观测结果所得到的知识, 可以更新对的认识, 即给出关于的后验分布密度; 5) 所谓基于观测值的射击成功概率, 是利用真值关于观测值后验分布对应的这个主观上假想的统计规律计算的。这样计算的概率含有主观成分, 可称为主观概率, 主观概率不能用重复试验的方法验证, 不能用于作战能力的评估, 可以用于决策者信念的支持, 依靠主观概率进行决策的正确性十分依赖于先验知识的精确性。

可以证明, 若用“目标速率真值取任何实数的可能性相同”描述先验知识, 即关于无任何先验知识且忘记了其不可能取负数, 则关于的后验分布为(,), 类似的结论对于关于,关于的后验分布同样成立, 即以往计算的概率是关于目标运动要素真值无任何先验知识的主观概率, 只有鱼雷运动误差的统计规律是客观的, 这时对于给定的目标运动要素观测值, 只需计算一次射击参数, 因而相对简单。

3 概率计算

主观概率和客观概率的计算方法相同, 所不同的只是模型及误差的概率分布, 其中客观概率

=(xÎ(–L/ 2,L/ 2) ) (7)

式中,x,需要表示为

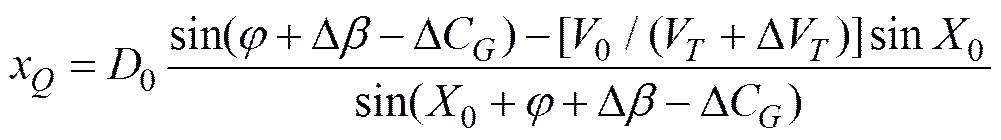
(9)

对于给定的,,,V, 令

= – 0.5L/,= 0.5L/(10)

=(, …,) (11)

其中

(, …,) = (D,D,DC,D,DV) (12)

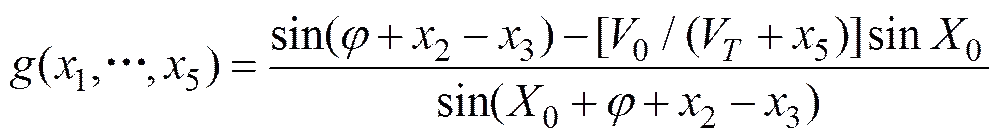
(14)

则上述概率可以表述为一般形式

=(Î[,] ) (15)

假设(D,D,DC,D,DV) 服从零均值正态分布, 即 (, …,)~(0,), 前面已经说明D,D,D应有一定相关性,不一定是对角矩阵, 若不考虑这些相关性, 则可以假设= diag(,,,,)。

计算概率的方法之一是蒙特卡洛法, 即仿真方法, 仿真方法计算的概率能客观地反映实际情况, 因而可以作为实际应用的参考, 以及作为对其他方法评价的标准, 这是仿真方法的主要优点。然而仿真方法计算的概率有一些不足, 主要表现为计算速度相对不足, 如为了得到一个数量级的计算精度, 可能需要成百倍地增加同一真值条件下的仿真次数, 另外, 同一条件下的不同次仿真结果一般总有波动, 用仿真方法计算的等概率线一般不光滑, 不能满足基于等概率线的其他问题的算法需要。为寻求快速准确地计算, 可以考虑解析方法, 设想的方法有

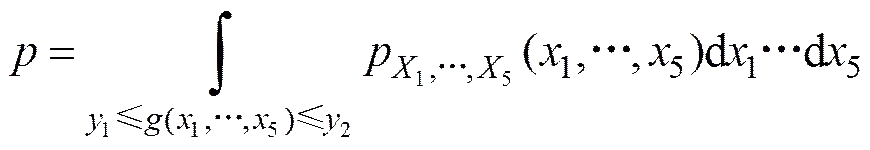
=(17)

这是一个1重积分, 用数值方法可以实现快速准确的计算。然而p()的解析公式一般很难给出, 因此, 可以考虑能用解决析公式表示的近似概率分布密度函数, 即若»p(), 则

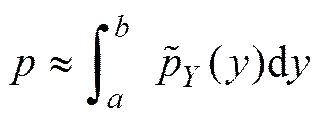
因为, …,为以0为均值的正态随机误差, 为得到=(, …,) 的近似概率分布函数, 可以考虑关于, …,的1阶近似

»=(0) +Ñ(0) (, …,)(19)

其中0 = 0表示1´5零向量,Ñ(0)表示()在0点的梯度行向量

Ñ(0) = (¶/¶, …,¶/¶)(20)

则的一个近似分布为(,), 其中

=(0) = 0 (21)

=Ñ(0)Ñ(0)(22)

对应的计算概率公式

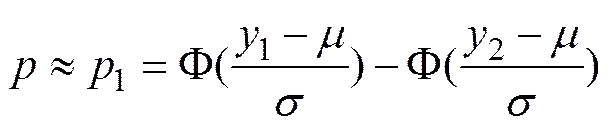
以下称之为1阶近似解析公式, 这个公式的计算速度不成问题。

当用上述公式计算的概率不满足精度要求时, 可以尝试关于, …,的2阶近似

»=+(, …,) (0.5)(, …)(24)

= (¶/¶x¶x)|(25)

其中,表示函数()在0点的Hessian 矩阵。

是一个关于正态随机向量的二次函数, 其对应近似分布密度还未见有现成的公式, 为此, 下面将其抽象为一个一般问题进行研究。

4 正态随机向量一般二次函数的分布

设~(,),= (, …,),为阶正定矩阵,为实常数,= (, …,)为实常数向量,为实对称矩阵, 记

=++(26)

则为正态随机向量的一般二次函数, 其分布由,,,,唯一确定, 下面的定理描述了这个分布的性质。

定理关于=++, 成立公式

=+++a(27)

Var=++b+ 2(++a) (28)

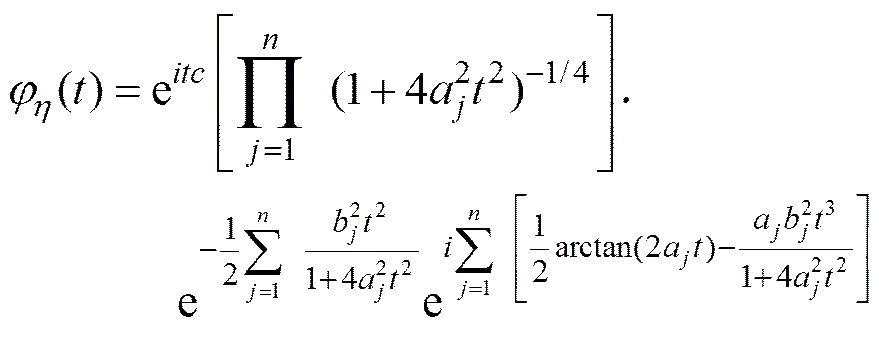
其中,, Var,()依次表示随机变量的均值、方差、特征函数。公式中的为满足=的可逆矩阵, 可取为的Cholesky分解,,,a为的特征值,为满足()= diag(,,a)的正交矩阵,,,b,的计算公式为

(,,b) = (+ 2)(30)

=++(31)

这个定理的证明此处略, 利用特征函数与分布函数的关系

可得

(33)

其中

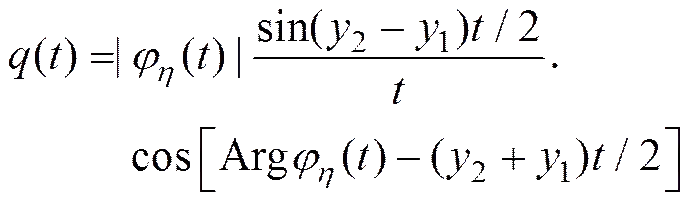
(35)

(36)

的取值可以结合关于|()|的估计给出, 一个简单的估计为

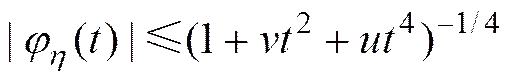
=(38)

计算程序取= 10, 这一方法可解决正态随机误差向量(各分量不一定相互独立、均值不必为0)函数的2阶近似对应的概率计算问题。

就直航鱼雷直进射击命中的客观概率而言,= 0,= diag(,,,,),= g(0) = 0,=Ñ(0),= 0.5, 以上述定理所述方法确定,,, 则

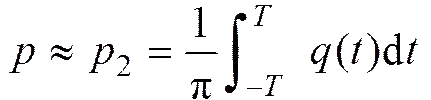
称这一公式为2阶近似解析公式, 被积函数()为以的变量的只与(,,,,)有关的函数, 可以用标准的数值积分方法计算。

5 仿真试验及对解析公式的评价

对于参数= 25 cab,= 25 kn,V= 50 kn,L= 150 m,= 2°,= 0.5°,= arctan(1/100) / 3,= 2 kn,= 1 kn, 取相同态势的仿真次数 N = 10,= 10 ~ 170°对应的不同态势下1阶近似解析公式、2阶近似解析公式计算的概率,与用仿真方法计算的概率满足|–­ | < 1/1000, |–­ | < 1/1000, 考虑到仿真方法计算概率的波动性, 10次仿真方法计算概率只能保证小数点后3位的精度, 因此, 上述解析方法的精度应远小于1/1000。就直航鱼雷直进射击命中概率的计算而言, 试验发现, 1阶近似解析公式比2阶近似解析公式相对精确, 且计算速度快, 因此可选用公式= 2[0.5L/()] – 1计算直航鱼雷直进射击的命中概率。同时这也说明, 在随机误差分析中, 用1阶近似确定正态随机误差函数的近似分布是一种可行的方法。

6 结束语

本文以直航鱼雷直进射击为例讨论了以往鱼雷射击随机误差分析不太关注的几个问题。主要结论及问题有, 目标运动要素误差应以目标的距离、速率、航向、方位误差表示, 只用目标的距离、速率、舷角误差表示将导致鱼雷实际航向相对计划航向的误差与舷角误差的相关性被忽略; 基于目标运动要素真值已知计算的概率是客观的, 对于现场鱼雷攻击决策者, 虽然鱼雷运动误差的统计规律可以看成已知的, 基于观测值计算的概率必含有主观成份, 与所使用的目标运动要素真值的先验知识有关且不能用重复试验的方法验证, 且不能用于作战效能评价, 只能用于决策信念的支持; 若关于目标运动要素无任何先验知识, 则主观概率的计算比较简单; 将鱼雷命中或自导发现目标的条件表示为随机误差向量函数对应的随机变量属于特定的区间, 利用函数的1阶、2阶Taylor近似公式可以给出的近似分布, 然后可用一重积分对应的解析公式近似计算概率, 其中在误差向量为正态分布的条件下, 1阶近似对应的计算公式可用标准正态分布表示, 2阶近似对应的计算公式利用了专门为此研究的一个定理, 若要求解析公式计算的概率与仿真方法计算的概率之差小于1/1000, 通常1阶近似解析公式就可满足要求, 这已为直进射击及其他射击方式的计算应用所证实, 就直航鱼雷直进射击而言, 1阶近似优于2阶近似; 不考虑解算过程导致的目标运动要素观测误差的联合分布, 随便假设目标运动要素各观测误差项相互独立的做法与实际不符, 有关数值试验也使用了这一假设, 因此这些方法和结论的可用性、系统性还有待进一步研究。

[1] 《现代数学手册》编纂委员会. 现代数学手册(随机数学卷) [M]. 武汉: 华中科技大学出版社, 2000.

[2] 主观概率.百度百科[EB/OL]. [2012-07-01]. http://baike.baidu. com/view/703605.htm.

[3] Jeffrey R. Subjective Probability[M]. United Kingdom: The Press Syndicate of the University of Cambridge, 2002.

[4] 于寅. 高等工程数学[M]. 武汉: 华中科技大学出版社, 2001.

[5] 周概容. 概率论与数理统计[M]. 北京: 高等教育出版社, 1984.

(责任编辑: 许 妍)

Discussion about Random Error Analysis of Torpedo Shooting

LI Chang-wen, REN Xing-zhe, WANG Peng

(Software Center of Science and Research Department, Navy Submarine Academy, Qingdao 266071, China)

Through the description of straightforward shooting of a straight running torpedo, the random error and some concepts of hitting problem are studied, and the difference between success probabilities based on true value and observed value of target movement element is pointed out. For objective probability, two analytic methods of computing probability are proposed based on the first order or second order approximation of the function of random error vector. According to a theorem about the formulas to compute the mean value, variance and eigenfunction of a common second order function of normal distributed random vector, an analytic method with the second order approximation is given. Results show that the two analytic methods have high precision, and the first order approximation method is better than the second order one in the case of computing the objective hitting probability of torpedo straightforward shooting.

straight running torpedo; random error; objective probability; analytic method

TJ630; E920.2

A

1673-1948(2012)06-0443-06

2012-05-01;

2012-07-05.

李长文(1962-), 男, 硕士, 副教授, 研究方向为随机过程、运筹学.