激光刻痕聚丙烯塑料失效破坏的参数识别*
王喜军,宗 智,聂 春,藤井睦雄
(1.大连理工大学运载工程与力学学部工业装备结构分析国家重点实验室,辽宁 大连 116024;2.大连理工大学运载工程与力学学部船舶工程学院,辽宁 大连 116024;3.帝恩(上海)软件科技有限公司,上海 200336;4.日本大协西川集团,日本 广岛 731-4311)
激光刻痕是通过激光加工手段去除部分材料形成的撕裂线,使材料的破坏裂痕沿指定的方式延展。这个方法最早用于包装工业,目前已经在各个工业领域广泛应用。在汽车仪表板设计中,将气囊的弹出通道覆于装饰性表皮之下,并且在仪表板背面布设撕裂线以确保安全可靠打开[1-3]。设置撕裂线是为了降低气囊弹出时破坏位置的结构强度,使气囊及时有效地展开,最大程度降低人员伤亡及财产损失;同时,由于撕裂线隐藏于仪表板下表面,与外界隔离,可避免磨损。
目前大部分车型都是通过激光设备在仪表板上加工撕裂线。激光加工出来的撕裂线由一排整齐的孔穴组成。在加工时仪表板并未完全被激光穿透,从而形成连续的锯齿形截面结构,如图1所示[4]。孔穴使仪表板结构强度沿着撕裂线弱化,当气囊展开时,仪表板也将同时沿着撕裂线翻转。
在塑料材料冲击性能研究方面,卢子兴等[5-6]、谢若泽等[7]对聚氨酯泡沫塑料压缩及剪切力学性能进行了实验分析;C.Ruff等[4]应用梁单元模型和替换材料计算了仪表板撕裂线的破坏。然而,撕裂线在加工过程中只是去除部分材料,并未使材料性质发生变化,同时塑料失效参数很难通过实验手段获得。因此,对撕裂线模型的建立及计算需要做进一步研究。本文中,就图2所示的撕裂线进行实验研究。得出不同工况下撕裂线失效的最大冲击载荷,并应用有限元计算软件LS-DYNA进行数值模拟。通过参数识别得出撕裂线位置的失效应变,为气囊展开冲击仪表板的数值模拟提供数据;同时应用极差分析方法得出聚丙烯(PP)材料的撕裂线布设直径和冲击速度变化对最大失效冲击载荷的影响。

图1 仪表板撕裂线截面图Fig.1 Section of instrument panel tear-line
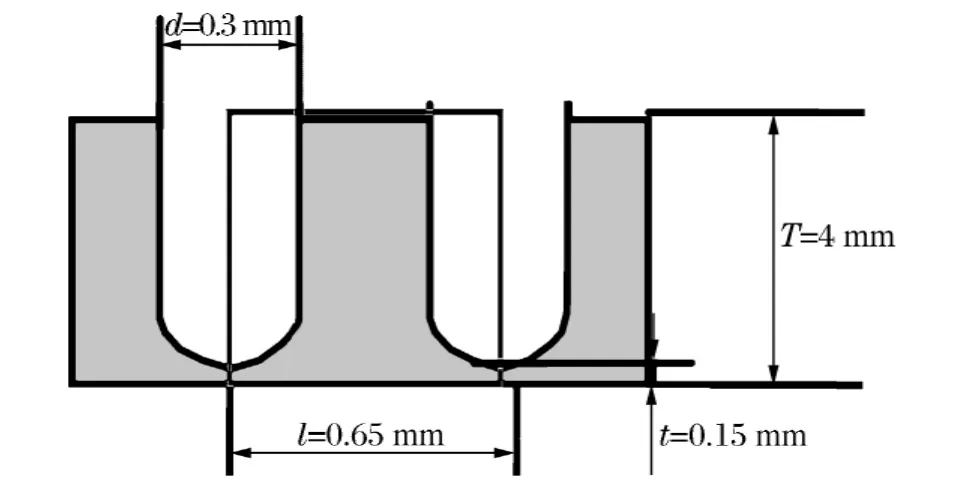
图2 仪表板撕裂线截面尺寸Fig.2 Section sizes of instrument panel tear-line
1 实 验
1.1 拉伸实验
塑料材料的力学特性会随应变率的变化而变化,因此,聚丙烯(PP)材料的拉伸实验在不同的速度下进行,拉伸速度分别为0.002、0.5、1、5和10mm/s。由实验数据得出这种PP塑料弹性模量为1.3GPa,泊松比为0.4,对应的真应力应变曲线见图3。
1.2 冲击实验
试件是一组140mm×140mm的方形PP塑料板,塑料板的中心位置用激光设备布设直径分别为30、50和70mm的撕裂线。试件的四周被夹持在两层钢板中间,钢板中心处设置比撕裂线直径大10mm的圆孔。
实验时,试件固定在冲击车床的一端,可动台车由另一端分别以10、15和20km/h的初始速度对试件进行冲击。可动台车的总质量为10.5kg,上方装有测量冲击过程中加速度变化的加速度计。图4为冲击实验设备图。通过采集加速度变化情况,可以得出撕裂线在破断失效过程中冲击载荷随时间变化的曲线。
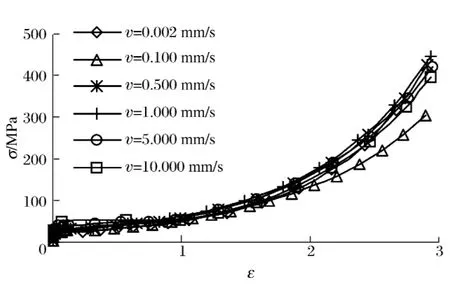
图3 PP塑料不同拉伸速度下的应力应变曲线Fig.3 Stress-strain curves of PP plastic at different tensiling velocity

图4 冲击实验装置图Fig.4 Apparatus of impacting experiment
2 有限元模型
2.1 撕裂线模型简化
由于仪表板上激光设备所加工的撕裂线尺寸较小,无法通过有限元方法直接建模。因此,在建立有限元模型时需要将撕裂线进行等效,使有限元模型撕裂线位置的截面积与试件相应位置截面积保持一致。另外,在撕裂线的位置通过定义单元节点的厚度形成厚度渐变的单元,这样就形成了孔穴的形状,与激光所加工的孔穴相似,如图5所示。
2.2 材料模型
有限元模型中,可动台车的冲击柱体用一个半球壳模拟;半球壳和固定试件的两层钢板在冲击过程中变形很小且对冲击实验的影响较小,可设为刚性材料;PP材料采用LS-DYNA中改进的分段塑性模型,材料特性由拉伸实验中测定的不同应变率下的应力应变曲线描述;同时,在材料描述上引入了另外两个失效准则,单元的塑性减薄和平面最大主应变,来描述撕裂线位置的失效行为[8]。
2.3 边界条件及初始条件
图6为实验的有限元模型,其中半球为冲击台车的前端圆柱形头部的简化模型;在冲击半球球心的位置设置质量单元,保证冲击半球的质量与可动台车的质量相等;在指定方向设置半球运动的初始速度;PP试件部分参照冲击实验装置,对相应位置的节点进行约束。
此外,模型中涉及到两部分的接触,冲击半球体与PP试件间的接触以及PP试件与上下钢板之间的接触。这两部分的接触均采用罚函数算法[9]计算。
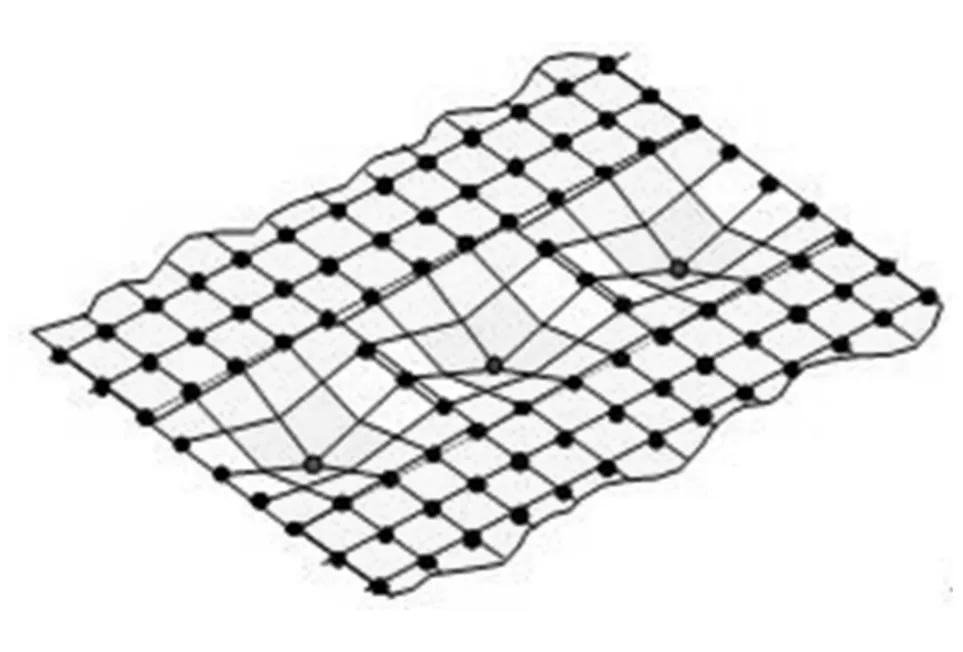
图5 撕裂线有限元模型示意图Fig.5 FEM model sketch of tear-line
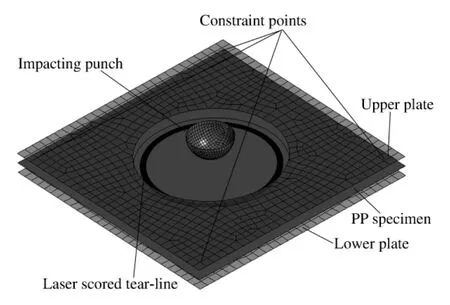
图6 冲击实验有限元模型Fig.6 FEM model of impacting experiment
3 失效参数的识别
参数识别是一种通过已知系统或物理过程中测量数据构建动态模型的数学方法。本文中应用了响应平面方法对材料参数进行优化,并将相对实验结果的误差最小化。在参数识别过程中涉及到两个主要方程,一是将均方差作为最小化目标,二是应用Min-Max方程最小化最大残差[10]。在计算过程中将残差合并到均方差范数方程中,可得
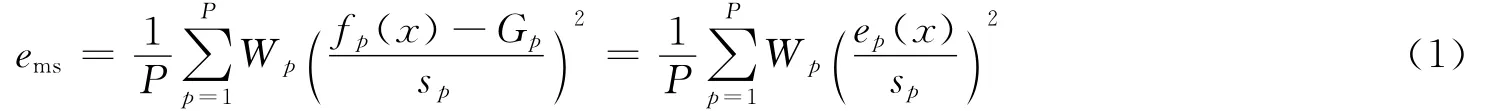
式中:ems为均方差范数,P为选区回归点的数目,Wp为加权量,sp为残差放大系数,fp(x)为计算值,Gp为实验测试值。根据式(1),参数识别的优化问题即转化为最小化残差的计算,得

在优化的过程中,将单次的冲击实验峰值作为测试点,材料模型中的失效应变作为变量,计算结果中球体与塑料板的接触力作为响应值,计算结果与实验数据的均方差作为优化目标。图7(a)~(b)为材料模型中厚度、平面方向的失效应变εf,t、εf,p与迭代次数n的关系。在优化计算过程中变量的上下边界随着变量的取值不同而发生变化,迭代结束时变量逐渐收敛,得到εf,t=0.072,εf,t=0.362。图7(c)为优化的均方差曲线,它随着迭代次数的增加趋于稳定,稳定值为0.007。
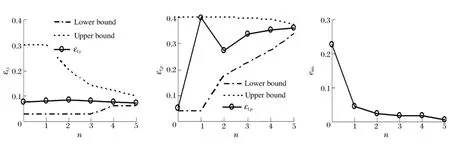
图7 迭代收敛过程Fig.7 The iterative convergence processes
4 结果分析
4.1 计算结果与实验结果的对比
冲击实验记录了整个过程中可动台车的加速度变化情况,根据台车质量可以计算得出冲击载荷的作用信息。图8为冲击载荷的有限元计算结果和对应的实验数据,其中每种情况进行了3次重复实验。实验中,在PP试件的撕裂线断裂以后,可动台车的不稳定振动导致数据也有所波动;而数值模拟中,在撕裂线破断后,冲击半球的加速度直接下降至零。这使计算曲线和实验曲线在撕裂线失效后存在差异。由图8可见,计算所得的曲线趋势与实验曲线一致,撕裂线失效时最大冲击载荷及失效时间也一致。
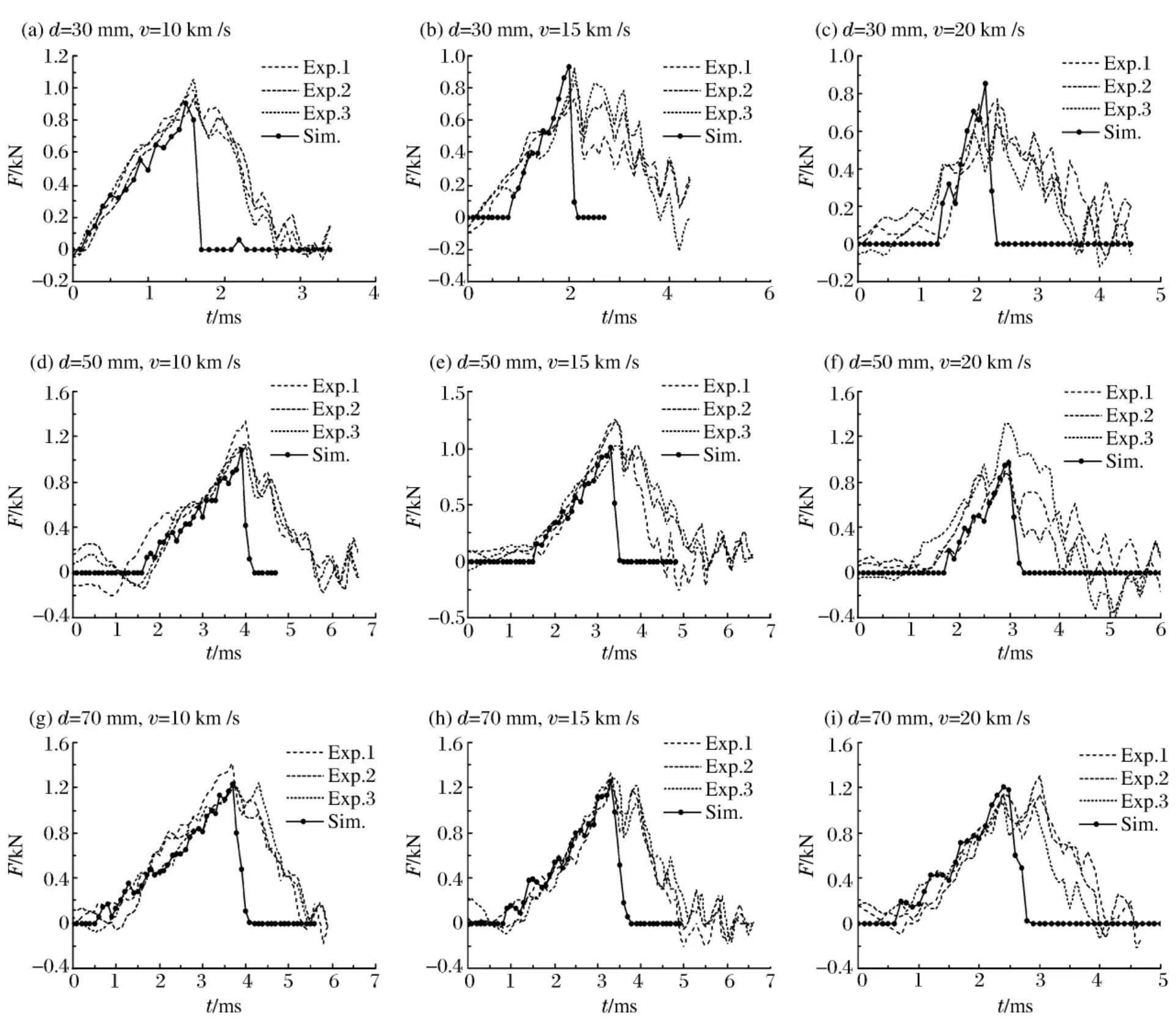
图8 冲击载荷曲线Fig.8 Impact load curves
4.2 极差分析
实验中涉及两个因素,一是撕裂线尺寸,二是可动台车冲击速度,这两个因素都各自包含三个水平。这里,通过极差分析[11-12]得出每个因素对撕裂线所能承受最大冲击载荷的影响。表1中列出了不同工况下所对应的最大冲击载荷,其中实验最大冲击载荷为三次实验最大冲击载荷的平均值。表2为极差分析表,其中∑Fm是某一因素下所有水平指标之和,¯Fm分别是同一因素下各指标的平均值,极差RFm是最大值与最小值的差,差值越大说明该因素对指标的影响越明显。从极差分析的结果可以看出,撕裂线直径对失效最大冲击载荷影响较大,而冲击速度对失效最大冲击载荷的影响不十分明显。

表1 最大冲击载荷Table1 The max impacting load
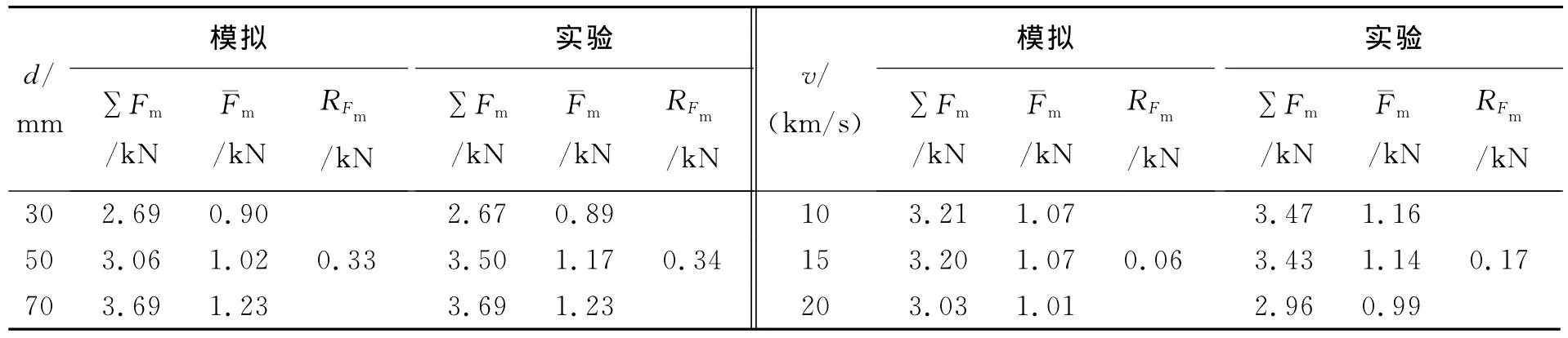
表2 极差分析Table2 Range analysis
5 结 论
对带撕裂线PP材料的最大冲击失效载荷分别进行了实验和数值计算研究,得出了可以信赖的数值计算数据,计算结果表明,有限元数值计算结果与实验数据吻合较好。从数值结果与实验的对比分析中,可以得出以下结论:
(1)LS-DYNA中改进的分段塑性模型在描述PP塑料失效行为时与实验数据吻合较好。结合实验数据对失效应变进行系统识别,确定εf,t=0.072,εf,t=0.362。计算所得PP塑料撕裂线失效的趋势与实验相符,最大冲击失效载荷及失效时间与实验数据一致。
(2)在PP塑料撕裂线简化上采用等效截面法,同时结合变节点厚度单元的使用,保证了模型与试件最大程度的物理相似。结果表明,这种简化模型能够有效地解决此类带撕裂线材料强度计算问题。
(3)带撕裂线的PP塑料最大冲击失效载荷随撕裂线直径增大而增大,随冲击速度增大而减小。
[1]Timothy L F.Vehicle instrument panel with seamless airbag cover:United States of America,EP0898524B1[P].1998.
[2]Skelly J M,Bondar R C,Hornburg F J.Method of processing a laser scored instrument panel with an invisible seam airbag opening:United States of America,US006657158B1[P].2003.
[3]Hayashi S.Airbag cover,instrument panel,airbag device and airbag casing:Japan,US007556285B1[P].2009.
[4]Ruff C,Eichberger A,Jost T.Simulation of an airbag deployment in out-of-position situation[Z].LS-DYNA Anwenderforum,2006.
[5]卢子兴,田常津,韩铭宝,等.聚氨酯泡沫塑料冲击力学性能的实验研究[J].高分子材料科学与工程,1995,11(6):76-81.LU Zi-xing,TIAN Chang-jin,HAN Ming-bao,et al.Experimental investigation of the impact mechanical properties of polyurethane rigid(PUR)foam plastics[J].Polymeric Materials Science and Engineering,1995,11(6):76-81.
[6]卢子兴,田常津,韩铭宝,等.聚氨酯泡沫塑料在应力波加载下的压缩力学性能研究[J].爆炸与冲击,1995,15(4):382-388.LU Zi-xing,TIAN Chang-jin,HAN Ming-bao,et al.Investigation of the mechanical properties of compression on polyurethane rigid(PUB)foam plastics under stress wave loading[J].Explosion and Shock Waves,1995,15(4):382-388.
[7]谢若泽,卢子兴,田常津,等.聚氨酯泡沫塑料动态剪切力学行为的研究[J].爆炸与冲击,1999,19(4):315-321.XIE Ruo-ze,LU Zi-xing,TIAN Chang-jin,et al.Studies of dynamic shear mechanical properties of PUR foamed plastics[J].Explosion and Shock Waves,1999,19(4):315-321.
[8]Hallquist J O.LS-DYNA keywords user’s manual[Z].USA:Livermore Software Technology Corporation,2006.
[9]Hallquist J O.LS-DYNA theory manual[Z].USA:Livermore Software Technology Corporation,2006.
[10]Nielen S,Willem R,Trent E,et al.LS-OPT user manual[Z].USA:Livermore software Technology Corporation,2007.
[11]Telford J K.A brief introduction to design of experiments[J].Johns Hopkins APL Technical Digest,2007,27(3):224-232.
[12]Wu C F J,Hamada M J.Experiments:Planning,Analysis,and Parameter Design Optimization[M].United States of America:Wiley-Interscience,2000.

