5-维欧氏空间球面曲线的一个几何性质

薛艳日方，冯艳丽，李玲玲

(信阳师范学院数学与信息科学学院，河南信阳 464000)

5-维欧氏空间球面曲线的一个几何性质

薛艳日方，冯艳丽，李玲玲

(信阳师范学院数学与信息科学学院，河南信阳 464000)

利用Frenet公式讨论了5-维欧氏空间中球面曲线的几何特征，给出了判定一条空间曲线是球面曲线的一个充分必要条件.

Frenet公式；5-维欧氏空间；球面曲线

0 引 言

Frenet公式，是微分几何空间曲线理论的基本公式，在经典微分几何中占有十分重要的地位，可以由它导出曲线的诸多重要性质与定理[1-5].目前，学者已在3-维欧氏空间Frenet标架和Frenet公式的基础上，根据曲线基本向量的微商与基本向量之间的特定关系，构造出了4-维欧氏空间中沿空间曲线的Frenet标架.在此基础上，本研究把它推广到5-维欧氏空间情形，并利用推广后的Frenet公式讨论了5-维欧氏空间中球面曲线的一些几何特征，得到判定空间曲线是球面曲线的一个充分必要条件，并给出了相应证明.

1 基本概述

在4-维欧氏空间中，光滑曲线Γ:r=r(s)的基本向量α、β、γ、μ关于弧长s的微商可以用α、β、γ、μ的线性组合来表示，即，

其中，k1(s)、k2(s)、k3(s)分别为曲线Γ的第一曲率、第二曲率与第三曲率，s为弧长参数，由此有，

引理1 4-维欧氏空间中光滑曲线Γ:r=r(s)落在一个球面上的充要条件为，

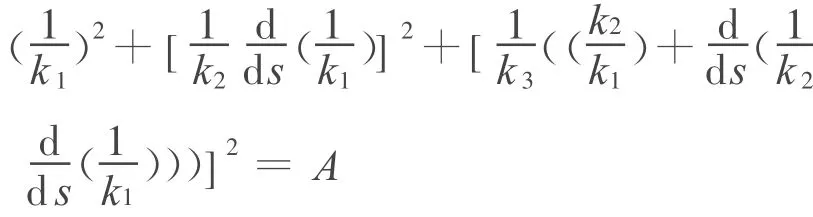
其中，A为常数，s为曲线Γ的弧长参数.

下面考虑5-维欧氏空间球面曲线的情形.设曲线Γ:r=r(s)是R5中的光滑曲线，其第一曲率、第二曲率、第三曲率与第四曲率分别为k1(s)、k2(s)、k3(s)、k4(s)，且 k1(s)、k2(s)、k3(s)、k4(s)都不为非零常数，其中，k1(s)、k2(s)、k3(s)、k4(s)分别简记为 k1、k2、k3、k4.则其基本向量α、β、γ、μ、ω关于弧长 s的微商可以用α、β、γ、μ、ω的线性组合来表示，则5-维 Frenet标架:{r(s):α，β，γ，μ，ω}可以定义如下，

这组公式的特点是，基本向量α、β、γ、μ、ω关于弧长s的微商可以用α、β、γ、μ、ω的线性组合来表示，其系数组成了反对称的方阵，

2 主要结果与证明

定理1 5-维欧氏空间中曲线Γ:r=r(s)落在一个球面上的充要条件为，

其中，A为常数，s为曲线Γ的弧长参数.

证明

1)必要性.

设球面方程为，

其中，s为弧长参数，R0为球面半径，上式两端关于s求导得，

又因为球面上的任意一向量都可由基本向量线性表示，所以，可以设不全为零的系数λ(s)、m(s)、h(s)、p(s)、q(s)使得，

对式(1)两端关于s求导得，

由此得到如下方程组，

式(1)两边同时点乘向量α，可以得到，

故，解此方程组可得如下等式，

将式(2)带入式(1)得，

对上式两边取模得，

恒成立.

2)充分性.

由题设，

其中，A为常数，对上式两端关于s求导可得，

上式两边同时乘以k4，可得，

将式(4)带入式(3)得，

应用5-维Frenet标架可定义r0如下，

对上式两端求导可得，

所以，曲线，r=r(s)落在一个球面上.

命题得证.

注:本研究所用方法可以推广到更高维的欧氏空间Rn(n≥6)中，进而可以得到Rn中的球面曲线的几何特征，并能得到类似的充分必要条件.

:

[1]梅向明，黄敬之.微分几何[M].北京:高等教育出版社，2008.

[2]梅向明，王汇淳.微分几何学习指导与习题选择[M].北京:高等教育出版社，2004.

[3]陈维桓.微分几何[M].北京:北京大学出版社，2006.

[4]吴大任.微分几何讲义[M].北京:高等教育出版社，1959.

[5]Carmo M P.曲张与曲面的微分几何[M].北京:机械工业出版社，2006.

One Geometrical Property of Spherical Curve in 5-dimensional Euclidean Space

XUE Yanfang，FENGYanli，LI Lingling

(College of Mathematics and Information Science，Xinyang Normal University，Xinyang 464000，China)

Abstract:Frenet formula was used to discuss the geometrical properties of spherical curve in 5-dimensional Euclidean space.Necessary and sufficient condition wasgiven to determine that one space cure is spherical curve.

Key words:Frenet formula；5-dimensional Euclidean space；spherical curve

O186.11

A

1004-5422(2012)04-0327-04

2012-07-20.

河南省教育厅自然科学基础研究(2011A110015)资助项目.

薛艳日方(1979—)，女，硕士，讲师，从事微分几何与非线性分析研究.