基于结构模型的磁性基底反演

于会臻，刘 展

（中国石油大学 地球资源与信息学院，山东青岛 266555）

基于结构模型的磁性基底反演

于会臻，刘 展

（中国石油大学 地球资源与信息学院，山东青岛 266555）

常规磁性基底反演方法往往忽略基底磁性变化采用常磁化强度模型，这里分析了其中的局限性，提出了先构建相关搜索重磁三维定量反演技术的变磁化强度模型，然后通过Parker界面反演算法进行基底反演。其中，对反演磁化强度所需磁异常分离采用了小波变换方法，并分析了该方法的关键技术和措施。通过利用该方法对某工区进行了实际资料处理后，得到较好效果。

磁性基底；变磁化强度；Parker；相关系数；多尺度分析

0 前言

由于古中生代及第三纪沉积岩层和第四纪疏松沉积为无磁性、或者弱磁性的，所以磁性基底作为磁性地层的上界面时，通常为前寒武纪的结晶基底，由岩浆岩或变质岩组成。在一般情况下认为，居里等温面为磁性地层的底界面。研究磁性基底界面无论对于研究盆地的形成与演化，还是对于研究矿藏的分布（如油气形成、运移、赋存等），都有极其重要的理论和实际价值［1］。目前，磁性界面反演方法主要有切线法、人机交互解释法、Parker迭代反演算法、欧拉算法、模型反演法、频谱分析法、样条函数法［2］。在实际应用中，主要采用的是切线法和人机交互解释法。常规反演方法通常采用简单的常磁化强度模型进行处理，但由于磁性基底相关异常是由基底界面起伏和基底磁性变化共同引起的，因此，往往出现反演结果与实际情况相悖的现象。针对该问题，作者在本文提出了先构建变磁化强度模型，再进行Parker磁性界面反演算法［6］的新磁性基底反演方法。

1 方法原理

Parker算法是七十年代R.L.Parker提出的一种界面重磁正反演公式，由于它能计算物性横向变化的连续界面，速度快，所以很快得到了广泛的应用。其基本原理为：

设地下界面S上部磁化强度J1为零、下部磁化强度J2不为零，平均深度为H，其在海拔水平面上的观测磁异常为式（1）。

式中 m表示分步积分的项数；n是指数项展开成级数的项数；Ml成为磁化强度函数。

ζn－m－l为界面函数，F［Mlζn－m－l］为界面函数的频谱，则界面的反演迭代公式见式（2）及式（3）。

式中 ω为径向圆频率，第（j－1）次得近似值，右端的为第i次的近似值，一般先给定△h初值，代入公式右端，求出△h，经反变换得到△h1；然后作为△h的下一次迭代的初始值，如此这样反复直到结果满足给定精度［2］。

针对算法中高频因子eωh影响迭代收敛性的问题，前人做出了有效的解决方案［6］，其算法虽然对磁化强度Ml对进行了假设，但用一个通用公式很难描述实际情况的磁化强度的分布。事实上，不仅仅是Parker界面反演算法，目前磁性基底反演中都或多或少地存在缺乏磁化强度约束问题，通常采用均一值视磁化强度模型（即设磁性基底的地层磁性参数为一常数），很少对基底磁性变化进行讨论［2］。

按均一值视磁化强度模型做界面正演（见图1）可知，忽略基底磁性变化，会使得对观测磁异常的处理全部假设为完全由磁性界面的构造引起。图1中的磁性基底浅会产生磁异常高值，磁性基底深会出现磁异常低值。因此，不合理的磁化强度模型假设得到的磁性基底反演结果，可能会在某些区域呈构造反转（见图1）。为解决该问题，作者将利用相关搜索重磁三维定量反演方法，构建一个接近实际情况的磁化强度模型，以便在Parker基底界面反演方法中增加有效的基底磁性约束。

图1 构造反转示意图Fig.1 Tectonic reversal

1.1 视磁化强度模型的构建

1.1.1 视磁化强度反演方法原理

与界面反演一样，磁化强度反演也存在严重的多解性问题，从公式（1）中可以看出，它们两者其实互为约束，即在求解过程中存在着互相制约的矛盾关系。同时，由两者产生的磁异常是无法由观测异常中准确分离的。因此，需要构建的磁化强度模型不可能是一个精确的模型，其目标应是找到由已知地质资料及观测数据所反映磁性基底磁性宏观分布，采用的方法为概率成像与位场约束扩展结合的方法。

在作者提出以下模型构建方法之前，首先假设已得到了磁化强度所引起的基底相关磁性磁异常磁异常的分离方法，将在1.2节中进行详细讨论。

由本节开头所得结论，磁化强度模型构建的目标是一种基底磁性的宏观反映，因此对物性单元的剖分也应体现这一点。将磁性基底界面与居里面之间地层剖分成若干个规则直立六面体形体单元（见下页图2），六面体高度的不同反映了地层的起伏，反演所得六面体磁化强度值主要反映了基底磁性横向的宏观变化，该处磁化强度定量反演方法采用了文献［3］提出的，以单相关系数为基础构制目标函数的多维黄金分割法。其关键技术是引入了多元线性回归分析中的相关系数R，具体表达式见参考文献［3］。R的物理意义是模型理论场与观测场之间的误差方差与观测场本身方差的逼近程度其目的是求取模型与观测数据的拟合组成的目标函数的极小来获得物性值的解。R的取值为0～1越接近“1”说明观测场与核函数的相关性越好；反之则越差。使得R最接近“1”的物性模型，就是反演最优解。算法在解的逼近问题上采用了n维黄金分割最优化方法，反演速度较快。但该算法如大多数磁化强度反演算法一样，对已知钻井信息的利用率较低且反演采取由浅到深的顺序易产生上层剖分网格占据大部份异常值的“上漂”现象。

为得到更合理的反演结果，作者提出了双重约束机制。该机制的提出鉴于以下假设：①由于剖分网格与观测场之间有一定的映射关系，找到这种关系即可确定任一剖分网格对于整个场的贡献大小按照贡献值大小进行反演，可使存在场源体可能性大的区域先分配场值从而避免“上漂”；②由于地质体赋存空间内磁化强度值必然存在着一定的连续性且能体现在所引起的磁场相关性特征中，以往简单的钻井点约束可利用该特征对附近剖分网格进行磁化强度约束空间的扩展。根据以上假设，约束分为磁化强度概率成像约束和基于钻井的位场特征约束。

图2 磁性基底剖分图Fig.2 Magnetic basement dissection figure

（1）视磁化强度相关概率成像约束。利用概率成像方法［4］，通过位场数据与场源体核函数相关获得场源体成像范围进行约束信息提取。当观测面为水平面时，位于地下q（xq，yq，zq）点磁体元在XYZ三个方向分量的概率函数为：

其意义是，通过计算场源体与实测磁异常的核函数与实测磁异常，在一定窗口范围内的归一化互相关得到观测场，是由任一剖分单元产生的概率，并利用该值搜索场源体磁化强度分布。由于ηq为一互相关结果，其绝对值不大于“1”。该值越大，表明q点越可能存在异常源；反之，表明存在场源体的可能性越小。利用磁异常垂直分量，可计算出，取其中绝对值最大者的数值和符号作为q点场源发生的概率。ηq值为正说明存在的异常源与扫描函数中的场源极性相同，为负值表明极性相反。

当得到概率值后，选取0～1间的阈值对其进行二值化。经多次试验证明，阈值选0.5～0.8之间比较合适。将概率值小于阈值的赋“0”，大于阈值的赋“1”，之后选取一定的搜素半径对二值化结果进行八方位领域搜索，将在搜索半径内相邻都为“1”的剖分单元组成一个闭合空间，便可找出场源体磁化强度的成像范围。利用该成像范围既可以概率值的大小确定上述多维黄金搜索算法中的搜索顺序，又可为后续磁场特征约束扩展方法做准备。

（2）基于钻井的位场特征约束。一般的反演方法仅局限于沿井筒进行线约束，即只对井筒穿过的单元进行约束。针对该问题，作者借助场源体分布与磁异常有较强的相关性，将钻筒约束扩展为体约束（见图3）。

图3 钻井约束扩展示意图Fig.3 Quantitative constraint expansion

任一场源点（ξ，γ，ζ）在计算点（x，y，z）处的磁异常写成如下形式（仅考虑垂直磁化的情况）：

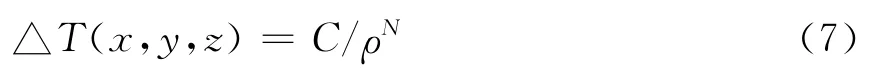
其中 △T为或磁力异常；C是不依赖于xyz的常数；ρ为测点和场源点的距离；ρ＝［（ξ－x）2＋（γy）2＋（ζ－z）2］1/2。

当场源与观测面足够远或场源足够小时，近似为点源，N＝2。对式（8）分别对x、y、z求导，得：

表1（见后面）是通过模型试验研究得到的磁异常△T的半极值、水平一阶导数△Tx的正负极值、垂向导数△Tz和△Tzz的零值水平区间距L与场源体横向分布L0的之间的关系。

由下页表1可知，L/L0的比值越接近“1”，说明对异常体水平边界刻画越准确。因此在同一埋深时，利用磁异常的垂向一次导数零值范围圈定场源体横向赋存空间最准确。按该结论便可对钻井附近的剖分网格磁化强度值约束区间进一步扩展，视位场特征边界范围内的剖分网格为磁化强度值接近的场源体。

1.1.2 磁性基底磁性磁异常分离与基底反演

针对磁性基底反演可将实测总异常划分为：

（1）基底上部地层引起的磁异常。该异常趋势变化主要是由浅部地层的强磁性体（如侵入性火成岩）引起的，由磁异常正演公式知，其离观测面距离相对较近，因此通常具有频率高、变化剧烈的特点。而且其中相当一部份强磁性体分布与断裂有较好的相关性。

（2）基底界面与居里等温面之间地层引起的磁性基底相关磁异常。该异常中包含了磁性基底起伏与基底磁性变化共同的影响。不同磁性的变质岩作用不同：副变质岩磁性较弱，正变质岩磁性较强。大部份区域地层磁性相对较弱，其引起的磁异常可看作是一种构造异常，反映的是基底起伏的贡献，为区域异常。而各种强磁性变质岩的横向分布变化所引起的磁异常，更多地反映了基底磁性分布情况，为局部异常场。因此，磁性基底相关异常可表达为弱磁性区域异常f0（M0）、中等磁性异常f1（M1）和强磁性异常f2（M2）三部份。其中M0、M1、M2分别代表弱磁性、中等磁性、强磁性区域。同时从实际勘探情况来看，基底起伏通常比较平缓，f0（M0）频率相对较低，而f1（M1）和f2（M2）频率相对较高。要对基底磁性进行宏观描述，其实就是寻找与中、强磁性异常特征。

上述的讨论可按如下步骤对观测异常进行分离。首先消除火成岩等浅部地层磁性体的影响，得到磁性基底相关磁异常，该异常是基底界面反演所对应的磁异常。圈定火成岩的方法为利用重力数据垂向二次导数处理、地震资料划分工区内主要断裂构造，并借助航磁垂向一次导数精确圈定出火成岩位置。之后，利用多次滑动趋势分析选取合适的半径逐步从实测异常中消除火成岩的干扰。

其次，从磁性基底相关磁异常中分离f0（M0）与f1（M1）、f2（M2），该异常分离得到的是磁化强度反演对应的磁异常。作者提出了小波变换的互相关系数方法，小波分离的关键在于小波函数的选取与分解阶次的确定。磁性基底相关磁异常的n阶尺度小波逼近反映的是具有低频特征的区域磁异常随着尺度的增大，小波逼近对应的频率信息也逐渐降低。与之对应的磁性基底相关磁异常与小波逼近的差值为剩余磁异常，反映的是浅层高频信息。由本节开始的定性分析讨论可预测，当小波分解尺度到某一阶数n后，小波逼近对应的低频信息将对应仅由弱磁性地质体及界面引起，而且，由于小波具有时～频定位特点，小波逼近系数（an＋i（i＝1，2…，m））分布不会再随尺度继续增大出现明显变化。因此，可采用相邻尺度下的磁性基底相关磁异常小波逼近系数的互相关系数来判断分解尺度。随着分解阶数的增加，an＋i（i＝1，2，…，m）相邻互相关系数越来越接近“1”；尺度an之前的an－1次小波重构函数所反映的是基底中、强磁性区域所引起的磁异常，因此在两个尺度的小波系数分布之间，必然存在较小的相关性且呈震荡起伏。在互相关系数呈渐进增大时，前an－1尺度下的小波重构函数就可以作为基底磁性相关异常。需要注意的是，在计算互相关系数前，需要对小波逼近系数进行归一化处理。在互相关系数突变点不明显时，可以通过功率谱分析的方法，确定其各阶所反映场源的平均深度。利用Bowin的公式，计算相应深度的大地水准面异常与小波分解的细节结果对比，从地球物理意义方面，可增加最高阶次分解结果的合理性［14］。

2 模型试验

测网为20 000m×20 000m，点距、线距都为500m，参数如下页表2所示。模型1～3为三处浅层火成岩磁化强度值，模型4～10为磁性基底部份强磁化强度值。磁性基底平均磁化强度为50× 10－1A/m，试验中设实际磁性基底为深度5km的平界面，居里等温面为深度20km的平界面。对视测磁异常进行3km趋势化分析，剥离掉火成岩引起的磁异常，则磁性基底相关区域磁异常如下页图4所示。作者对该结果选用了“Bior3.5”小波进行16阶的离散小波变换，得到小波系数的互相关系数如下页图5所示，可知尺度8的重构函数为基底磁性相关磁异常。概率成像阈值选为0.5，进行重磁三维定量反演得到视磁化强度模型（见下页图4（b））。最后利用图4（b）的磁异常和基底及居里等温面的初始模型进行Parker磁性界面反演算法，得到磁性基底界面如图6（b）（见后面）。

表1 异常特征值水平范围L与异常体宽度2a的关系Tab.1 Abnormal eigenvalue level Land abnormal body width 2arelationship

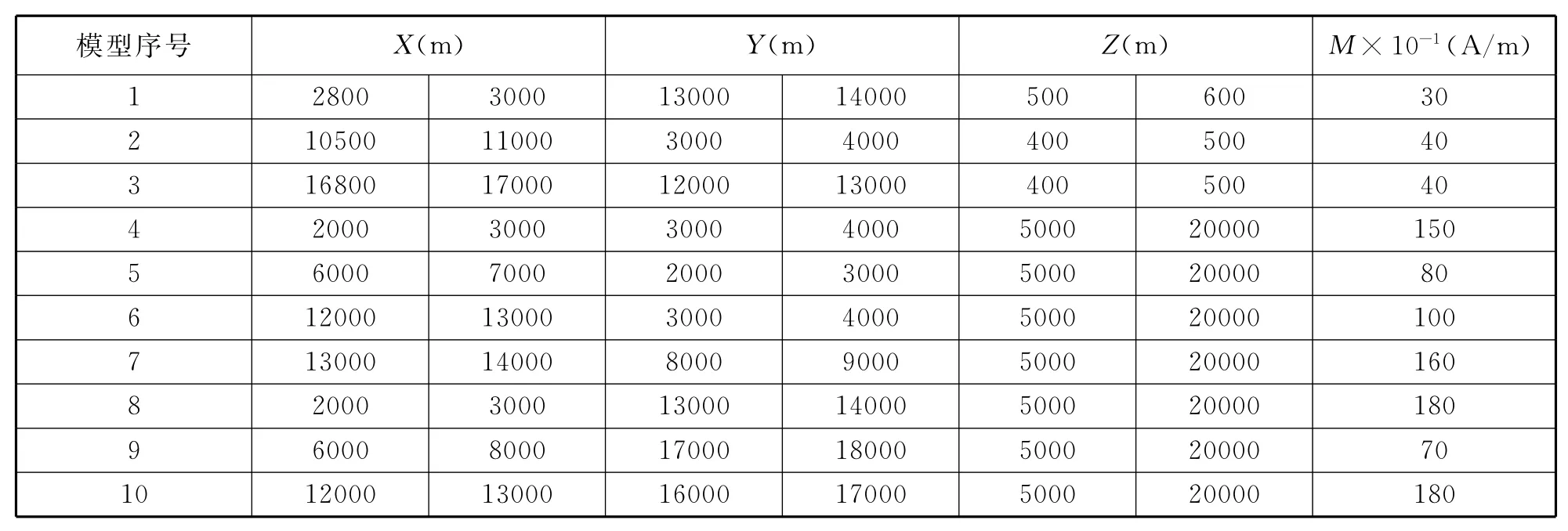
表2 模型参数Tab.2 Model parameters

图4 模型磁异常处理Fig.4 Models of magnetic anomaly processing

结果分析可知：①下页图6（a）为利用均一化磁化强度模型的磁性基底反演结果，反响基底反演结果起伏较大，深度分布在5 000m±230m左右，且走势与观测磁异常变化相近；②利用本文中的方法构建的基底磁化强度模型，与初始模型比较吻合，所得基底界面深度（见下页的图6（b））分布在5 000m ±20m。采用本文的方法可较好地降低出现构造反转的可能性，增加了反演结果的合理性。

3 野外资料处理

表3 钻井深度Tab.3 Drilling depth

通过对中国辽东湾某工区进行磁性基底反演验证了方法的适用性。该区磁测资料已进行化极和曲化平处理。该区域七口钻井集中于工区中南部，深度达2km左右（如表3所示），同时结合该工区构造，经分析知磁性基底界面为西低东高，西部深处可达为5km左右，居里面深度在20km左右，对其中间地层进行网格剖分可知，X、Y剖分间隔为500m，Z方向不剖分。

作者首先利用重磁资料对工区内断裂分布进行划分，同时由化极磁异常的垂向一次导数进一步确定火成岩位置，选用5km半径趋势化分析得到去除火成岩后的磁性基底相关磁异常（见下页图7）；接着，选用“Bior3.5”小波对磁性基底相关磁异常进行16阶的离散小波变换，则由小波变换尺度9的重构函数得到基底磁性相关磁异常。由已知的地质资料可粗略确定每个剖分单元的视磁化强度值的上限和下限，视磁化强度相关概率成像约束中阈值选0.7，经反演得到视磁化强度分布；最后，借助得到的磁化强度模型，利用Parker算法进行磁性基底深度界面，反演结果如上页图8所示。由此可见，工区内磁性基底呈东西成带、南北分块的特征，并且南低北高、西低东高，对比已知井资料可知误差在100m～200m之间，结合已知地质认识，反演结果趋势及深度比较合理。

4 结束语

作者在本文对磁性基底反演采用了一种新的思路和尝试，在研究Parker界面反演算法的基础上，提出了基于单相关系数多维黄金分割搜索方法的磁场概率成像及位场特征值约束机制的磁化强度模型构建方法。其中，反演过程中的磁异常分离利用了小波不同尺度变换之间的互相关关系，对模型及实际的工区的处理得到了较好的效果。

由于位场反演本身存在的严重多解性问题，还有许多处理步骤需要进一步研究，构建更加符合磁异常特征的小波基函数，将会对异常的提取具有更强的物理意义和更好的实际效果。磁化强度模型构建所采用的概率成像扫描函数，可以采用导数方程，这样更有利于对磁性体边界的确定，钻井约束扩展方程的进一步修改也将会提高约束精度。

［1］ 刘光鼎，郝天珧，刘伊克.重磁研究对认识盆地的意义［J］.地球物理学进展，1996，11（2）：1.

［2］ 赵百民，郝天珧.反演磁性地质界面的意义与方法［J］.地球物理学进展，2006，21（2）：353.

［3］ 刘展，班丽，魏巍，等.济阳坳陷花沟地区火成岩重磁成像解释方法［J］.中国石油大学学报，2007，31（1）：30.

［4］ RAFFAELE ALAIA，DOMENICO PATELLA，PAOLO MAURIELLO.Imaging multipole gravity anomaly sources by 3Dprobalility tomography［J］Journal of Geophysics and Engineering，2009，3（6）299.

［5］ 班丽.相关约束重磁三维定量反演方法研究［D］.东营：中国石油大学，2009.

［6］ 相鹏，刘展.双界面模式Parker算法磁性界面正反演方法［J］.中国石油大学学报：自然科学版，2009，33（1）：37.

［7］ 汪炳柱，徐世浙，刘保华，等.多次插值切割法分场的一个实例［J］.石油地球物理勘探，1997，32（3）：229.

［8］ 段木春，徐世浙，阎汉杰，等.划分磁异常场的插值切割法在研究火成岩体分布中的应用［J］.石油地球物理勘探，1998，33（1）：125.

［9］ MARK E.ANDER，STEPHEN P.Huestisl.Gravity ideal bodies［J］.Geophysics.1987（52）：1265.

［10］孙鲁平.基于密度成像的综合速度建模方法研究［D］.东营：中国石油大学，2007.

［11］PAOLO MAURIELLO，DOMENICO PATELLA Localization of maximum－depth gravity anomaly sources by a distribution of equivalent point masse［J］.Geophysics，2001，66（5）：1431.

［12］姚长利，郝天珧，管志宁，等.重磁反演约束条件及三维物性反演技术策略［J］.物探与化探，2002，26（4）253.

［13］段木春，范典高.利用插值切割法研究磁性基底局部起伏特征［J］.石油物探，1999，38（4）：89.

［14］刁博，王家林，程顺友.重力异常小波多分辨分析分解阶次的确定［J］.中国地质大学学报，2007，32（4）564.

［15］于德武.用等效磁源法进行磁异常转换［J］.物探化探计算技术，2004，26（2）：133.

［16］吴文鹂，管志宁，高艳芳，等.重磁异常数据三维人机联作模拟［J］.物探化探计算技术，2005，27（3）：227.

［17］梅岩辉.均质多面体重磁异常正演计算表达式的一致性［J］.物探化探计算技术，2007，29（1）：33.

book=107,ebook=107

1001—1749（2012）03—0295—08

P 631.4

A

10.3969/j.issn.1001－1749.2012.03.10

于会臻（1981－），男，汉族，山东桓台人博士，研究方向为地球探测与信息技术。

国家重大专项（2008ZX05020－006）

2011－07－31改回日期：2012－03－20