航天器椭圆轨道自主交会的鲁棒滑模控制

卢 山，夏永江

（1.上海航天控制工程研究所，上海 200233；2.上海航天技术研究院，上海 201109）

0 引言

!随着载人航天技术逐步成熟和空间站发展的需要，空间交会对接技术的作用将越来越重要。自20世纪60年代以来，世界上已进行了100多次空间交会对接活动。从技术发展角度看，交会对接技术将逐步向自主交会对接（AR＆D）方向发展［1－2］。一方面，对一些载人交会对接难度大、成本高的任务，利用自主交会技术可有效节约成本，降低任务风险，提高任务的可行性；另一方面，对有人参与的交会活动，利用自主交会技术可减轻航天员的压力，并通过手动与自动方式的组合，提高任务的可靠性。

早期的交会对接控制多采用C－W脉冲制导，包括R－bar、V－bar、最优二脉冲、多脉冲制导等［3－5］。但上述各种交会控制均为开环，制导精度较低，不适于航天器的自主交会。对此，对人工势函数法、模糊控制法、滑移算法等多种基于C－W方程的闭环控制方法进行了研究［6－8］。但基于C－W方程的开环控制和上述闭环控制方法均仅适于圆轨道，这源于相对动力学方程（即C－W方程）的局限性。

因椭圆轨道的相对运动方程存在时变参数，需依据航天器自身的轨道信息计算获得，故针对运行于椭圆轨道上的目标星进行自主交会须实时获得绝对轨道的信息。但在某些特殊条件下，如两星飞行轨迹超出地面测控站的监测范围，或在火星等行星附近进行自主交会，地面站无法实时传送定轨信息，或针对失效的航天器进行自主交会，两星无法建立通信联系等时，主动星就无法获得时变参数的大小，因此需设计不依赖这些参数的自主交会控制律。目前，针对目标航天器运行于椭圆轨道，且缺少绝对轨道信息的自主交会对接研究较少。文献［9］利用全系数自适应控制方法设计了相应的控制律，实现了仅依靠相对状态信息的自主交会，但需设计多个增益因子，增加了控制律设计的复杂性。

为此，本文根据目标航天器运行于椭圆轨道的两星相对运动方程，在仅依赖相对运动信息的条件下，对用不确定系统的鲁棒滑模控制方法设计自主交会控制律，以实现参数未知时的自主交会进行了研究。

1 椭圆轨道相对运动方程

设空间交会中，两星的相对位置关系如图1所示。图中：T，A分别为目标航天器和追踪航天器。定义轨道坐标系So：原点为目标航天器质心；z轴沿径向指向地球；x轴垂直于z轴且沿速度方向；y轴与x、z轴构成右手坐标系。

图1 相对位置矢量Fig.1 Relative position vector

两星的相对运动方程的矢量形式为

式中：rT，rA分别为目标航天器和追踪航天器相对地球的位置矢量；Δr为追踪航天器相对目标的位置矢量；μ为地球引力常数；u为追踪航天器的控制加速度；t为时间。

将式（1）在目标航天器的轨道坐标系中展开，可得完整的两星相对动力学方程为

若目标航天器运行于圆轨道，且两星相对距离与目标航天器至地球距离之比为小量，则式（2）中为常值，方程右边只保留一阶小量，可简化为线性常系数相对运动方程，即C－W方程［10］。若目标航天器运行于椭圆轨道，则均为时变量，式（2）保留一阶小量可得椭圆轨道的相对运动方程（Lawden方程）

根据式（3）的相对运动方程设计自主交会的控制律，必然要求获知目标航天器轨道参数，但此3个量均为时变，如无法实时获得，就需设计不依赖其的自主交会控制律。

2 不确定系统鲁棒滑模控制

将式（3）中的时变参数视为不确定量，构成一不确定相对运动系统，则可用不确定系统的鲁棒滑模控制理论实现参数未知时的自主交会。

首先将Lawden方程写成状态方程形式

式中：

整理式（4）可得

式中：η＝DX；ΔA＝BD。此处：

变结构滑模控制对系统的参数和干扰不确定性具有较强的鲁棒性，其设计一般分为两个独立步骤：

a）选择理想滑动模态超平面（滑动面）；

b）设计某种控制律将系统的状态驱动至滑动面上，并将该状态保持在滑动面上，使之渐近趋向系统的平衡点［1、11］。

本文选择的系统滑动平面为

式中：P为正定对称矩阵，是代数Riccati方程的解，且有

此处：α为大于0的常数；Q为正定对角阵，均可由设计者选择。

根据变结构滑模控制的定义和设计步骤，系统状态的运动由两部分构成：第一部分是在变结构控制律作用下，将系统状态由状态空间中的某点驱动至滑动面S（X，t）＝0上（滑动模态的可达性）；第二部分是系统在滑动面附近，并沿S（X，t）＝0的滑模运动（滑动模态运动的稳定性）。系统的动态品质取决于上述两部分。为改善系统的动态品质，对第一部分可设计某种控制律使系统状态以有限的速度趋向滑动面。

2.1 到达运动控制律

对式（6）求导，并代入式（5）可得

令到达运动控制律为

将式（8）代入式（7）可得

其中，可先取

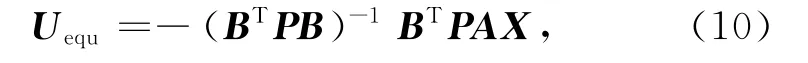
则有

选择非线性状态反馈控制

式中：ε为设计者选择的趋近速率，且ε＞0；

此处：k＝max‖D（t）‖。

这样，采用式（10）、（12）之和构成的控制律以及式（6）的滑动面，系统的滑动模态为趋近可达。

证明：令Lyapunov函数V＝STS，则有

组合式（12）可得

综合式（13）和式（14）右端的最后两项，可得

将式（15）、（16）代入式（14），有

根据文献［12］的Barbalat引理可知

因此，滑动模态是渐近可达。

2.2 滑动面稳定性

考察系统在滑动面S＝BTPX＝0上的稳定性。取Lyapunov函数V＝XTPX，则求导后可得

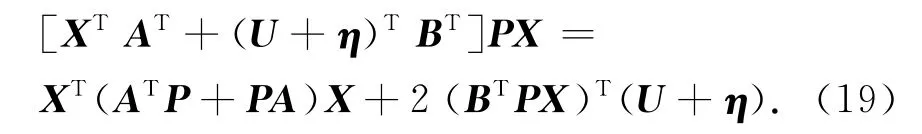
在滑动面上，有S＝BTPX＝0，则对任意常数α＞0，有

将式（7）代入式（20），可得

式中：λmin为Q的最小特征值。由此可知：系统在滑动面上具有渐近稳定的滑动运动。

3 仿真

取航天器初始轨道要素见表1，初始时刻追踪星在x轴上落后目标星1km，要求最终的相对位置为Xf＝［－10 0 0］Tm，相对速度为＝［000］Tm／s。表1中：a，e，i，Ω，ω分别为卫星轨道半长轴、偏心率、倾角、升交点赤经和近地点幅角。两种不同情况的到达运动和滑动面参数见表2。

表1 两星初始轨道要素Tab.1 Initial orbit elements of two spacecrafts

表2 两组仿真参数Tab.2 Two groups of simulation parameters

采用第一组参数时相对位置和相对速度分别如图2、3所示。由图可知：在此条件下可实现航天器的自主交会，交会所用时间为2.5×104s。主动航天器的三轴加速度如图4所示。由图可知：其最大值为10－4m／s2量级。整个交会过程共需速度增量为4.58m／s。

采用第二组参数时相对位置和相对速度分别如图5、6所示。由图可知：在此条件下自主交会所需时间较短，约5 300s，且因控制律参数的改变，增大了追踪航天器的控制加速度（其量级为10－2m／s2），较第一组参数的最大加速度提高了2个量级，故其相对位置的变化速度也变快，自主交会共需速度增量35.29m／s，明显大于第一种情况。

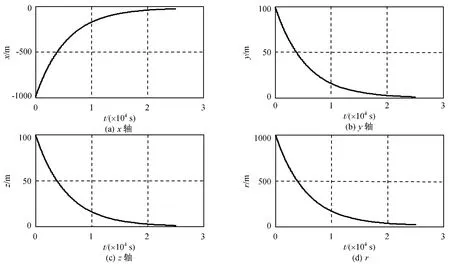
图2 情况1的相对位置变化Fig.2 Relative position in case 1

图3 情况1的相对速度Fig.3 Relative velocity in case 1

图4 情况1的追踪星控制加速度Fig.4 Control acceleration of the chase in case 1

图5 情况2的相对位置Fig.5 Relative position in case 2

比较两组不同参数结果可知：控制律参数选择决定了自主交会所需时间，以及在交会期间所需最大加速度和总速度增量。若追踪航天器为小卫星，并选择小推力发动机作为推力器，则可选择交会时间较长的参数，这样既能保证推力输出要求符合实际推力器的工作能力，又可减少交会所消耗的燃料。若常规航天器和推力器，则可选择交会时间较短的参数，提高任务的快速性，但交会消耗的燃料会相应有所增加。

4 结束语

针对缺少绝对轨道信息情况时的椭圆轨道下自主交会任务，本文采用不确定系统的鲁棒滑模控制设计了自主交会的控制律。仿真结果表明：所设计的控制律能有效实现预期的交会目标，可用于完成在无法实时定轨时的椭圆轨道自主交会任务。

图6 情况2的追踪星控制加速度Fig.6 Control acceleration of the chase in case 2

［1］POLITES M E.An assessment of the technology of automated rendezvous and capture in space［R］.NASA TP－1998－208528，1998.

［2］ZIMPFER D，KACHMAR P，TUOHY S.Autonomous rendezvous，capture and in－space assembly：past，present and future［R］.AIAA 2005－2523.

［3］YAMANAK K，YOKOTA K，YAMADA K，etal.Guidance and navigation system design of R－bar approach for rendezvous and docking［R］.AIAA 98－1299.

［4］PRUSSING J E.Optimal four－impulse fixed－time rendezvous in the vicinity of a circular orbit［J］.AIAA Journal，1969，7（5）：928－935.

［5］PRUSSING J E.Optimal two and three－impulse fixed－time rendezvous in the vicinity of a circular orbit［J］.AIAA Journal，1970，8（7）：1221－1228.

［6］LOPEZ I，MCINNES C R.Autonomous rendezvous using artificial potential function guidance［J］.Journal of Guidance，Control，and Dynamics，1995，18（2）：231－241.

［7］BENNIS R J，CHU Q P，MULDER J A.Adptive fuzzy control for rendezvous and docking by reinforcement learning［R］.AIAA 2001－4354，2001.

［8］刘鲁华，汤国建，余梦伦.圆轨道近程自主交会轨道设计［J］.宇航学报，2007，28（3）：653－658.

［9］王 颖，吴宏鑫.基于椭圆轨道的空间交会停靠全系数自适应控制方法研究［J］.宇航学报，2001，22（5）：15－19.

［10］CLOHESSY W H，WILTSHIRE R S.Terminal guidance system for satellite rendezvous［J］.Journal of the Aerospace Science，1960，27（9）：653－658.

［11］杨盐生，贾欣乐.不确定系统的鲁棒控制及其应用［M］.大连：大连海事大学出版社，2003.

［12］SLOTINE J－J E，LI W P.Applied nonlinear control［M］.New Jersey：Prentice Hall International Inc，1991.