基于容差模型的发动机悬置系统稳健优化设计
王歆侃
(1.合肥工业大学 噪声振动工程研究所,合肥 230009;2.安徽省汽车NVH与可靠性重点实验室,合肥 230009)
人们对汽车乘坐的舒适度要求越来越高,发动机是汽车主要的振源,其振动经悬置系统传递给车架或车身,因而发动机悬置系统的参数设计对汽车整车减振来说非常重要。对于发动机悬置系统的优化设计,可以从不同角度提出目标函数和约束条件,并建立不同的数学模型。常见的目标函数主要有:发动机悬置系统六自由度完全解耦或是部分解耦,移频使系统固有频率处在合理的区间,系统的支反力(矩)最小或是传递率最小。考虑到研究的车型上的悬置位置和安装角度已经确定,因而以悬置的刚度为设计变量,主要从移频且使悬置系统部分解耦来进行多目标参数优化设计。悬置厂商提供的悬置垫,悬置刚度参数一般都有很大的可变性,主要来源于悬置材料的变化和悬置几何形状的变化。另外在悬置与支架等的装配过程中,往往会产生预应力以及悬置形状的扭曲,也将造成悬置刚度值的变化[1]。传统的确定性解耦优化方法往往忽略了悬置刚度值的可变性,忽略了刚度偏差对悬置系统解耦的影响,使实际的工况下解耦效果很不理想。基于对悬置参数不确定因素影响的考虑,应该选择一种方法一方面寻求目标函数的最优值,另一方面应该考虑设计变量的误差等不确定因素,这就需要我们在优化设计中结合稳健设计的思想,即稳健优化设计。本文将稳健优化设计应用于发动机悬置系统的解耦优化中,充分考虑了各种干扰和设计变量的变差情况,不仅保证设计结果的合理性,同时也保证设计结果对悬置参数的不敏感性。同时利用Monte Carlo方法对结果进行分析验证,对悬置刚度对系统性能的影响程度进行研究。
1 稳健优化设计模型
传统确定性优化模型为:
式中:x,xL,xu分别为设计变量及其上下界; f (x)为目标函数;gi(x)(j=1,2,L,m)为 m 个约束函数。
稳健优化设计中,不仅考虑目标函数均值μf变化,而且要考虑目标函数的标准差σf的变化。均值μf和标准差σf的计算,可以通过泰勒级数展开来近似。考虑变量相互独立,则目标函数的均值和标准差分别为:
对于约束函数,由于变量变化因而引起约束的变化,于是原问题的约束变为:
同时为了表示设计变量偏离的可行性,相应的设计变量的边界变为:
(2)、(3)式中 n 为任意常数,当 n=3,x随机变差时,其设计的可行率可达到,能满足实际要求。
综上,稳健优化模型为[3]:
2 发动机悬置系统优化模型
2.1 悬置系统理论模型
发动机悬置系统可简化模型为:通过三个或四个三维的粘—弹性元件悬置支承在车架上,具有六个自由度。图1为四点悬置布置模型。发动机总成的坐标系原点选在总成质心处,平行于曲轴中心线为X轴,指向发动机前端,Z轴平行于气缸中心线,指向发动机缸盖,Y轴按正交坐标系的右手定则确定。θx、θy、θz分别为绕 X 轴、Y 轴和 Z 轴的转角。
利用拉格朗日方程可推导出系统振动微分方程为:
式中:[M ] 为系统的质量矩阵, [K ]为系统的刚度矩阵,[C ]为系统的阻尼矩阵,{q }=[x,y,z,θx,θy,θz]T为六个广义坐标列向量, {F(t) }= [ fx,fy,fz,fθx,fθy,fθz]T为系统所受激励向量。
对系统进行固有频率和固有振型的计算,只需考虑无阻尼自由振动情况,系统微分方程为[M ][K ]{q}={0 }, 可计算得到悬置系统的六阶固有频率 ωj(j=1,2,L,6)和固有振型[φ ]。
2.2 能量法解耦
发动机悬置系统六自由度振动耦合往往导致发动机振幅加大,振动频带过宽。由此需要对其进行解耦设计。从能量的角度去评价悬置系统的耦合程度[4,5],由振动微分方程得到的系统的固有频率和固有振型。当系统以第j阶模态振动时,定义能量分布矩阵为:
式中:φ(k,j),φ(l,j)分别为第 j阶振型的第 k 个和第l个元素;M(k,l)为系统质量矩阵的第k行、第l列元素;ωj是第j阶固有频率。
当系统以第j阶模态振动时,第k个广义坐标分配的能量占系统总能量的百分比:
当其值为100%,则系统作第j阶模态振动时能量全部集中在k个广义坐标上,此时,该阶模态振动完全解耦。
2.3 悬置系统稳健优化模型
设计变量:发动机悬置系统特性与发动机及其变速箱等的质量,转动惯量,悬置的安装位置、安装角度及其悬置主刚度值等因素有关。但是考虑到发动机和变速箱的本身的特性不能改变,同时悬置的安装位置和角度已经确定,故而以悬置的主刚度值K1、K2、L、Ks(i=1,2,L,s)为设计变量,其中 s 为悬置主刚度个数。
优化目标:
式中:Eθx、Ez分别为侧倾自由度上能量百分比和垂向自由度上能量百分比;w1、w2分别为侧倾自由度上能量百分比和垂向自由度上能量百分比的加权因子。
约束条件:(1)悬置位移不能过大,过大的位移既容易使悬置剪切破坏,又使使用寿命降低,因而悬置主刚度不能过小,即(i=1,2,L,s);(2)悬置系统的最大固有频率必须小于发动机自身激励频率1/的,才能起到隔振效果 。最小激励频率为怠速下的着火脉冲f=N·n/30C(N为汽缸数,n为曲柄转速(r/min),C为冲程数),使有更好的隔振效果,则取悬置系统最大固有频率为fmax≤N·n/30C。另外还需要避开车身的扭转振动频率、车身垂直跳动频率、路面激励频率等,综上取悬置系统固有频率范围为5≤f≤N·n/30。即:
综上,由式(2)~(5)将以上模型转化为稳健优化模型:
式中:n取为3。
2.4 最优化方法
考虑到该优化模型为两目标优化问题,需要使用多目标优化算法。同时该模型设计变量多,优化目标与设计变量之间的函数关系复杂,存在许多局部最优解,需要选用合适的最优化算法。遗传算法隐含着并行性,能够同时搜索到多个局部最优解,利于找到全局最优解。而如果将多目标问题通过加权组合法等转化为单目标问题,则无法发挥遗传算法的优势。将Pareto最优解方法和遗传算法结合构成多目标优化设计的Pareto遗传算法[6],能计算得到多目标优化问题的Pareto最优解集。此时从得到的最优解集中,根据具体的设计要求,选出最符合要求的解作为最终的设计结果。因而选择Pareto遗传算法来进行发动机悬置系统稳健设计。
3 优化实例
对于某具体的车型,该发动机为六缸四冲程的发动机,悬置系统为四点平置,左右对称布置。其怠速为n=800 r/min,则其点火脉冲频率为f=N·n/30C=40 Hz,则该悬置系统的固有频率要满足fmax≤N·n/3=28.3 Hz。悬置系统的质量参数、定位参数及其刚度参数分别如表1~3所示,优化前系统的固有频率及能量分布如表4所示。

表1 悬置系统质量参数 kg·m2
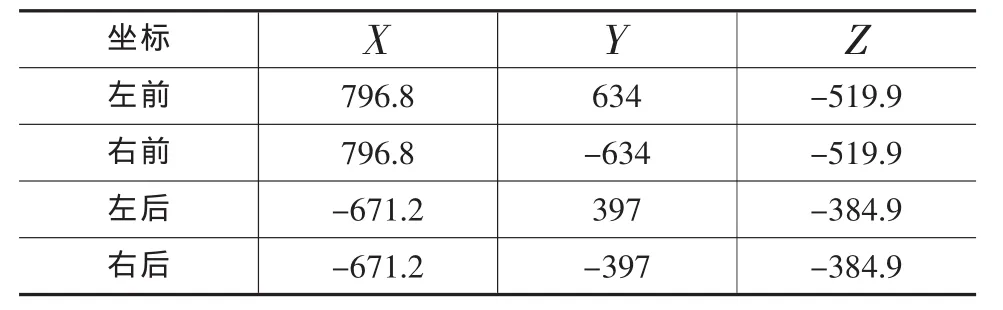
表2 悬置定位参数 mm

表3 优化前各悬置刚度值 N/mm

表4 优化前系统固有频率与能量分布 Hz
由表4可以看出,部分频率分布间隔过小,最高固有频率过大,且各转动轴方向的解耦度较低,其中侧倾方向的解耦度只有78.53%,耦合较严重,需要改进。
采用Monte Carlo法分析悬置刚度对振动耦合能量分布的影响。假定刚度值按正态分布,变化范围±10%,以4个悬置的刚度作为自变量对原系统进行鲁棒性分析,经过1 000次随机试验分析,得到垂直和侧倾方向解耦度的Monte Carlo图,如图2和图3所示。
可以看出,垂直方向的解耦度分布较合理,最低与最高解耦度差值为 4.19%,标准差为0.6%,而侧倾方向的解耦度分布不甚合理,最低与最高解耦度差值为 15.25%,标准差为 2.39%,稳健性较差。
利用稳健优化设计模型,采用Pareto遗传算法,对动力总成悬置系统的刚度参数进行优化,优化后各悬置刚度值如表5所示,系统各阶固有频率与能量分布如表6所示。
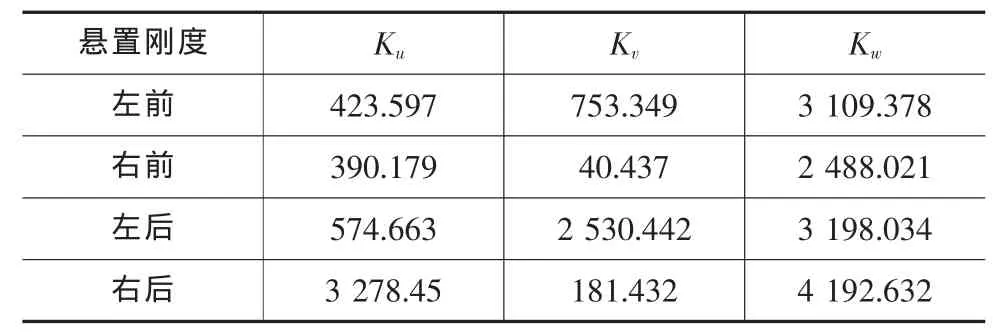
表5 优化后各悬置刚度值 N/mm
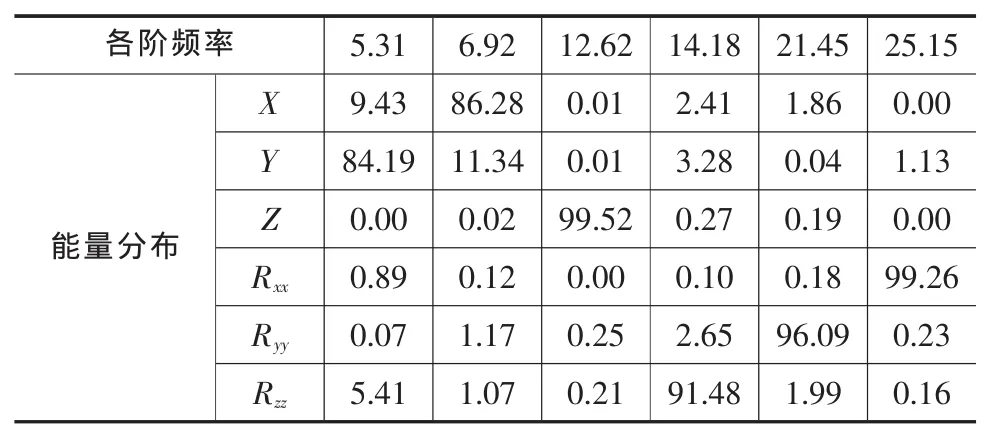
表6 优化后系统固有频率与能量分布 Hz
可以看出,与优化前相比,系统的各阶固有频率分布更加合理,最高频率有了较大的降低,各平动方向的解耦度有所降低,但各转动方向解耦度有了较大的提高,其中主要的侧倾方向由原来的78.53%提高到99.26%,系统的振动解耦有了较大的改善。
用同样的参数和方法对优化后的结果进行Monte Carlo分析,结果如图4和图5所示。
可以看出,优化后的垂向解耦度分布仍较合理,而侧倾方向的解耦度分布,最低与最高差值只有5.65%,标准差为0.6%,稳健性有了较大的提升。
4 总结
悬置刚度值的变差在实际中不可避免,悬置刚度值容差的减小意味着制造成本的提高。在不增加成本的前提下,需要有更好的方法对发动机悬置系统进行优化设计。本文在考虑悬置刚度变差的情况下,从解耦的角度,进行发动机悬置系统稳健优化设计。并且对结果进行Monte Carlo法分析,来决定优化结果在实际中的可行性。由文中的实例分析可得,稳健优化设计的结果比较满意。
[1] M Qatu,M Siraft and F Johns.Rostness of powertrain mount system for noise,vibration and harshness idle[J].Automobile Engineering,2002.
[2] 陈立周.稳健设计[M] .北京:机械工业出版社,2000.
[3]徐石安.汽车发动机弹性支承隔振的解耦方法[J].汽车工程,1995,17 (4):198-204.
[4]王景蓉,陈无畏.轿车动力总成NVH性能分析及悬置优化[J].汽车科技,2008,4:26-30.
[5]夏露,高正红,苏伟.Pareto遗传算法在气动外形优化中的应用[J].空气动力学学报,2007,25(2):194-198.

