基于小波域多尺度Retinex的复杂光照的人脸识别

高 涛

（长安大学信息工程学院，陕西西安 710072）

目前，对光照变化的人脸识别中，通常有以下几种处理光照变化的方法:基于传统的图像预处理方法，如直方图均衡、Gamma变换等;抽取具有光照稳健性的特征点方法［1］，对图像进行浮雕化处理（embossing）［2］和采用边缘图表示方法等;基于光照模型，比较典型的如光照锥（Illumination Cone）［3］、熵图像（Quotient Image）［4］、球谐函数（Spherical Harmonic）［5］等模型;基于人类感知模型，较为典型的是Retinex算法［6］，该算法利用了人的视网膜、大脑皮层构造亮度和颜色的感知模型，对光照变化图像的补偿有明显效果，但是图像的对比度和亮度的乘积较小。本文从人脸识别系统实用性角度考虑，借鉴Retinex理论的研究成果，提出了一种基于小波域多尺度Retinex模型（DWT－MSR）。该方法在二维小波变换后的小波域中，将其低频小波系数变换到对数空间，使用三种不同的高斯滤波系数和对数空间中的小波系数进行卷积操作，将三种标准偏差尺度下得到的结果进行加权平均，采用均值方差归一化的方法，对输出图像进行灰度值线性拉伸;小波域中其他三种高频系数保持不变，然后再将变换后的低频系数和高频系数作小波反变换，得到的新图像则为小波域多尺度Retinex模型的处理结果，最后使用定点独立分量分析和神经网络进行分类识别。从实验结果来看，在提高光照变化稳健性方面，该方法优于SSR、MSR以及直方图均衡、Log等传统图像处理方法。

1 DWT－MSR 介绍

1.1 Retinex

Retinex理论［7－9］于1963 年由 E.Land 提出，该理论是一种感知亮度和色度的计算理论，主要论述了人眼是如何获取外界图像的。E.Land基于Retinex模型，定义理想的图像 f（x，y） 为

式中:i（x，y）表示图像中的亮度，r（x，y）表示图像的反射函数。

E.Land引入了Center/Surround模型，后面的研究者在此基础上进行大量的研究，其中以Jobson的单尺度Retinex（Single－Scale Retinex，SSR）算法比较著名，算法的表达如下

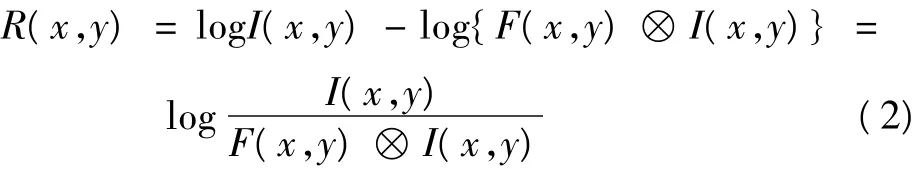
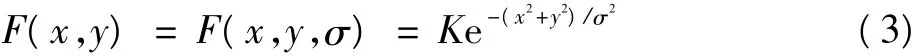
K值由下式来确定

式中:σ是计算的标准方差，σ的大小会对图像的效果有一定影响，直接关系到图像中能够保留多少细节信息，当选择比较小的σ时，虽然能够压缩动态范围，但是色感度较差;当选取较大的标准偏差时，色感一致性较好，但是动态范围的压缩就较差。通常都是在动态范围压缩和色感一致性之间寻找平衡点。但是单一尺度无法在图像动态范围和图像色感一致性之间做到很好的平衡，实际需要在这两方面都能取得完成好的性能，所以在此基础上改进单尺度Retinex（SSR）算法为多尺度Retinex（MSR）算法。

1.2 MSR

MSR的算法可以使用下式描述

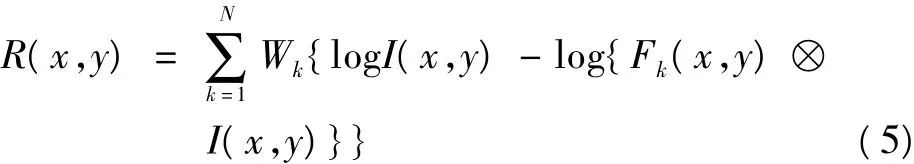
式中:Fk（x，y）表示由标准差σk决定的与（x，y）坐标点像素有关的一个环境函数，Wk表示与Fk（x，y）相对应的加权系数。多尺度Retinex变换能够较好地压缩图像的动态范围，同时能够保证图像的色感一致性。但是在选用σk仍然会将图像的部分高频细节信息给平均模糊掉，所以笔者提出了DWT－MSR算法，它不仅能够实现成图像的动态范围压缩和保证图像的色感一致性，并且能够保留图像的高频细节信息。

1.3 DWT－MSR

设输入图像为f0（x，y），其二维小波变换为

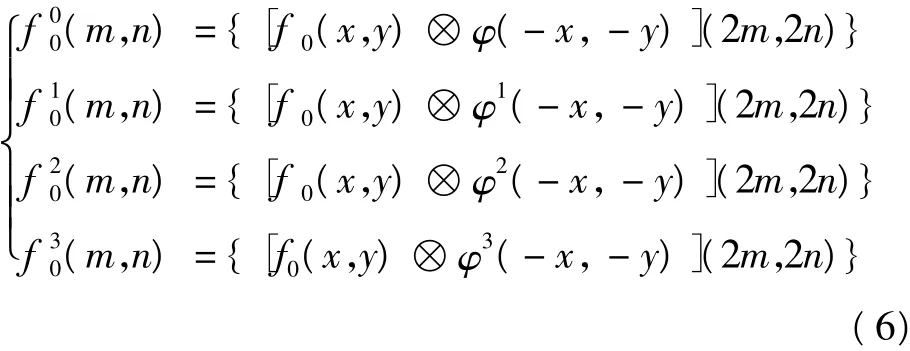
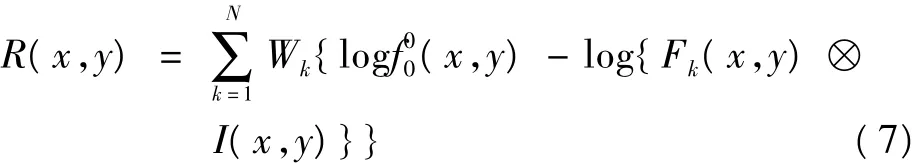
实验表明，对于大多数图像而言，选取大、中、小等3个尺度就可以满足动态范围压缩和色感一致性的要求，即N=3，然后加权系数并取其平均值。最终得到的R（x，y）会出现负值，即超出了显示的范围，使用Gain/Offset方法进行修正，如式（8）和式（9）所示

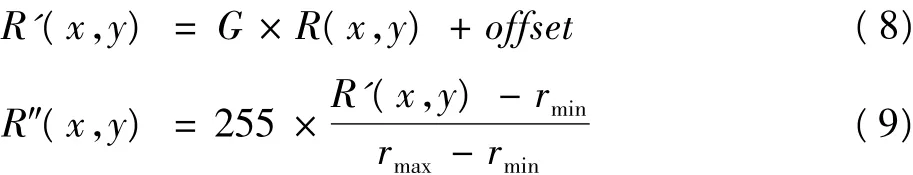
其中，R'（x，y）和R″（x，y）分别表示图像小波系数的变换输出值和修正后用来显示的灰度值，针对增益系数G和偏移量offset做了大量实验，结果表明这2个值可以取相对稳定的值，其中G取值为3，offset取值为50，rmin和rmax为修正后图像系数中的最小值和最大值。最终对修正后的低频系数和小波变换后的3组高频系数作二维小波逆变换，最终逆变换的结果为DWT－MSR的变换结果，整个过程如图1所示。实验表明，二维小波变换在分解层数上，单层分解和多层分解的识别率差距很小，平均识别率差值不大于1%，多层小波变换中计算量比单层大很多，所以本文算法中采用单层小波变换。

图2为SSR，MSR，DWT－MSR算法对一幅光照不均匀图像的作用效果，从视觉角度来讲，MSR的效果优于

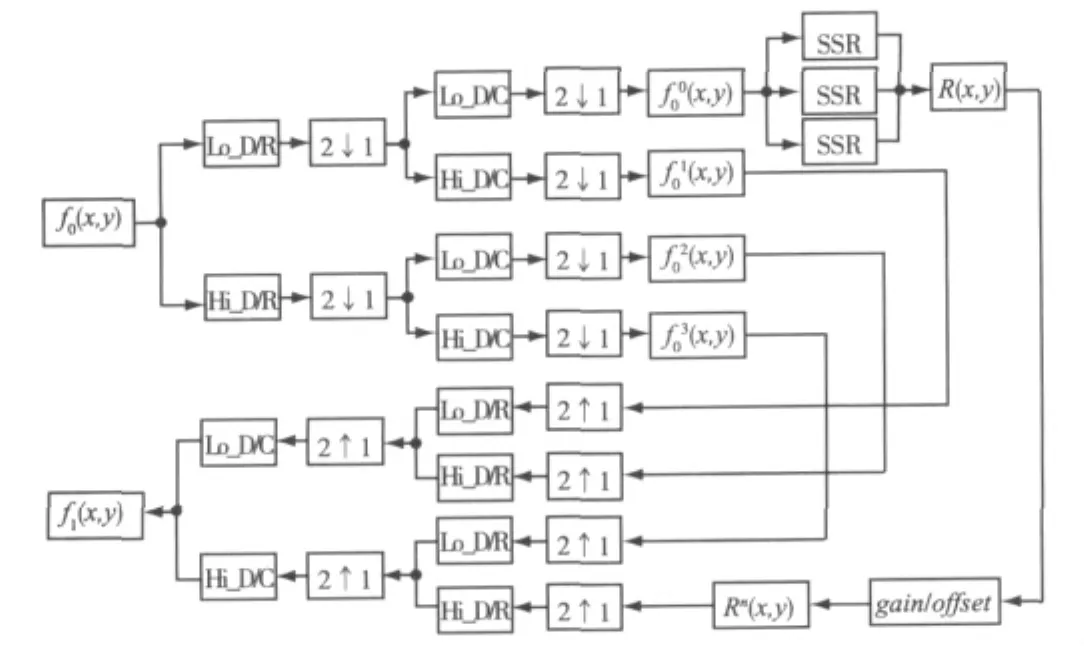
图1 DWT－MSR框图

SSR，DWT－MSR的效果优于MSR，这和上面的论述是相吻合的。

2 特征提取与分类识别

FPICA在进行信号降维时，同时考虑了信号的二阶和高阶统计特性，人脸的特征描述方面，许多比较重要的细节信息隐藏在的高阶统计量中，所以本文使用独立分量分析的方法，ICA的结构图如图3所示。

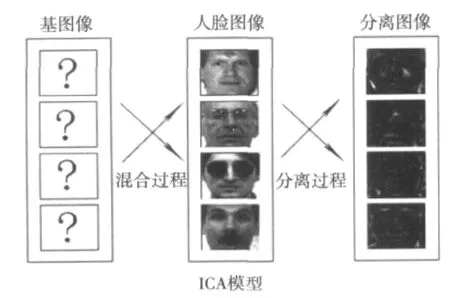
图3 ICA结构模型

设人脸库矩阵X=（x1，x2，…，xL）T为L个随机的观测量，每一个量都是由P（P≤L）个独立分量以进行线性组合，公式为

式中:A 为 L × P 的满秩矩阵，S=（s1，s2，…，sP）T，其中si是一个独立分量，它满足均值为零，方差为1的非高斯分布。通过迭代计算出A时，则有S=A－1X=WX，其中W=A－1。ICA的最终目标就是根据观测矩阵X，计算出独立分量S和混合矩阵A。

本文采用根据负熵判别准则分离独立分量的算法FastICA。算法可分两步实现:首先白化处理观测信号X为，有

白化过程可由PCA实现，再进行独立分量提取。

3 实验结果与分析

为了验证算法的有效性，在YaleB人脸数据库上测试该模型，取YaleB数据库中的10个人，每人45张照片，其部分图像如图4所示。按照光源与照相机间角度增加的顺序排列这些图像并将其分成2个子集，第1个是训练集，包含每个人的9幅图像，第2个是测试集，包含每人剩下的35幅图像。在每个测试过程中，共选取10余组人脸的训练样本。

图4 YaleB库部分图像

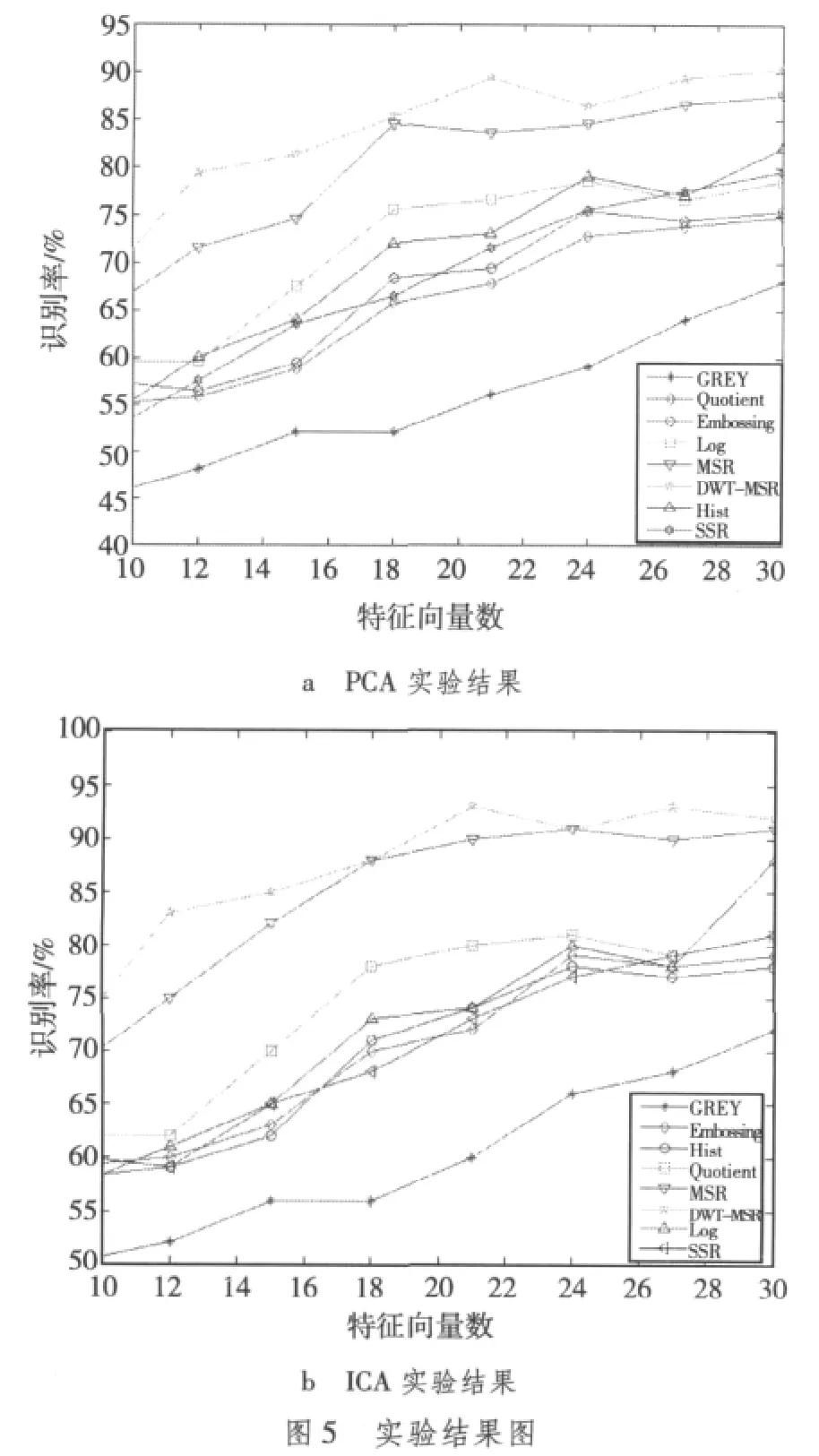
为了证明算法的有效性，对本文算法DWT－MSR与基于传统的图像预处理方法（直方图均衡（Hist）、Log算子）、抽取具有光照稳健性的特征点方法（Embossing）、基于光照模型（Quotient Image）方法、基于人类感知模型（SSR，MSR）等算法进行比较。特征提取使用 ICA和PCA等经典算法来实验。结果如图5所示，在相同的特征提取算法和分类器的情况下，DWT－MSR的方法明显优于其他的算法。这是由于DWT－MSR算法在考虑到图像均衡阴影部分的同时保留了图像的高频信息，变换后的图像不仅降低了光线的干扰，同时恢复了图像部分高频细节信息。独立分量同时考虑到信号的二阶统计特性和高阶统计特性，所以它的识别率明显高于PCA。基于神经网络的方法识别率明显高于传统的方法，而当数据量急剧增大时，神经网络算法尤其体现出了它对大样本分类的优势。

4 结论

笔者提出了一种基于小波域多尺度Retinex模型（DWT－MSR）。算法在二维小波变换域中，对低频图像作多尺度Retinex变换，保留图像的高频细节信息，最后再经过小波逆变换。通过实验证明，在提高光照变化稳健性方面，该算法优于SSR、MSR、直方图均衡以及Log等传统图像处理方法。由于ICA不仅考虑了信号的二阶统计特性，还考虑了高阶统计特性，所以性能优于PCA，当独立分量个数递增时，识别率得到了明显的提升。

：

［1］ADINI Y，MOSES Y，ULLMAN S.Face recognition:the problem of compensating for changes in illumination direction ［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，1997，19（7）:721－732.

［2］KOUZANI A Z，HE F，SAMMUT K.Towards invariant face recognition［J］.Information Sciences，2000，123（122）:75－101.

［3］GEORGHIADES A S，BELHUMEUR P N，KRIEGMAN D J.From few to many illumination cone models for face recognition under variable lighting and pose［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2001，23（6）:643－660.

［4］SHASHUA A，RAVIV T R.The quotient image:class－based reentering and recognition with varying illuminations［J］.IEEE Trans.Pattern A-nalysis and Machine Intelligence，2001，23（2）:129－139.

［5］BASRI R，JACOBS D W.Reflectance and linear subspaces［J］.IEEE Transaction on Pattern Analysis and Machine Intelligence，2003，25（2）:218－233.

［6］RAHMAN Zia－ur.Investigating the relationship between image enhancement and image compression in the context of the multi－scale Retinex［J］.Journal of Visual Communication and Image Representation，2011，22（3）:237－250.

［7］NAIK G R.An overview of independent component analysis and its applications［J］.Informatica（Ljubljana），2011，35（1）:63－81.

［8］WANG Ronggui.Image enhancement in the compressed domain based on Retinex theory［J］.Computer Research and Development，2011，48（2）:259－270.

［9］WANG Jinhua.Retinex－based color correction for displaying high dynamic range images［C］//2010 IEEE 10th International Conference on Signal Processing.［S.l.］:IEEE Press，2010:1021－1024.