永磁同步发电机与Boost斩波型变换器非线性速度控制
耿 强 夏长亮, 王志强 史婷娜
(1. 天津工业大学电工电能新技术天津市重点实验室 天津 300387 2. 天津大学电气与自动化工程学院 天津 300072)
1 引言
近年来随着风力发电技术的快速发展,风能在能源中所占的比重也迅速上升。1996年~2006年的十年间,全球风电装机容量年平均增速为 28.6%,截止到 2007年末,全球风电装机总容量已接近94000MW[1]。直驱式永磁风力发电系统具有噪声小、可靠性高和维护成本低等优点;同时,系统采用全功率变换器与电网连接,低电压穿越能力较强,由于上述特点使其在近年来受到了广泛关注[2]。
直驱式永磁风力发电系统中一种常见的拓扑结构如图 1所示[3],其电机侧变换器由二极管整流桥和 Boost斩波电路组成,为叙述方便,文中将此结构称为Boost斩波型变换器。

图1 Boost斩波型直驱式永磁风电系统拓扑结构图Fig.1 Topology of the direct driven PMSG-based wind energy conversion system with boost-chopper converter
图1中,uA、uB、uC分别为发电机定子端电压;uo为二极管整流桥输出电压;iL为电感电流;udc为直流侧电压;L为Boost电路升压电感;S1为Boost电路功率器件;C为直流侧电容。
与三相桥式全控变换器相比,Boost斩波型变换器成本较低,结构较为简单,系统可靠性较高,并能在一定风速范围内实现最大风能捕获,很多学者已经对此类变换器进行了研究[4-6]。
永磁同步发电机、二极管整流桥和 Boost斩波电路均具有较强的非线性,目前的控制策略多为普通的比例积分(Proportional-Integral,PI)控制[4-7]。普通PI控制器具有设计简单和适用性好等特点,但其是基于目标误差的控制器,仅考虑了系统在某一运行状态附近的稳态模型,忽略了其瞬态特性,因而具有动态响应较慢的缺点;且非线性系统的 PI参数难于整定,很多参数通过经验和试算得到,这给实际应用带来了一定难度。
反馈线性化是一种较为常见的非线性控制方法,其核心思想是通过状态反馈和非线性变换将非线性系统代数地转换为全部或部分的线性系统,从而可以应用比较成熟的线性系统控制方法。由于在转换过程中并没有采用线性逼近的方法,即没有忽略高阶非线性项,因此该方法精确度较高。反馈线性化已广泛应用于电力电子[8-11]、电机控制[12-14]和分布式发电[15]等多个领域。
在现有的基础上,以表贴式永磁同步发电机(Surface Permanent Magnet Synchronous Generator,SPMSG)为研究对象,首先根据二极管整流桥的换相点,将发电机每个电气周期分为6个区间,在每个区间内对发电机和 Boost斩波电路进行整体非线性建模;然后分区间利用输入-输出反馈线性化方法将非线性系统转换为线性系统;最后根据线性最优控制原理对变换后的线性系统设计转速控制器,使系统具有良好的动态和稳态性能。
2 系统数学模型
2.1 SPMSG数学模型
SPMSG等效电路及空间矢量图如图2所示,图中,eA、eB、eC分别为发电机定子相反电动势;iA、iB、iC分别为发电机定子相电流;Ls为发电机定子等效相电感;Rs为发电机定子等效相电阻;ψPM为发电机转子磁链;ωe和θe分别为发电机转子电气角速度和电气角位置;A、B、C为三相静止坐标系,其方向为发电机定子绕组空间轴线方向;d、q为空间旋转坐标系,以角速度ωe逆时针旋转;ψPM与 d轴重合。

图2 SPMSG等效电路和空间矢量图Fig.2 The equivalent circuit and space vector diagram of SPMSG
由图2可得

由图2b中空间矢量定向方式,可得

式中id,iq——发电机定子d、q轴电流。
由发电机转矩方程和运动方程可得

式中pn——发电机极对数;
Tm——发电机输入机械转矩;
J——发电机转动惯量;
F——发电机摩擦系数。
2.2 Boost斩波电路数学模型
在系统正常运行范围内,通过配置合适的升压电感参数,可以使 Boost斩波电路工作在连续电流模式。设功率器件的开关信号为S(t),其占空比为d,由文献[16]可以建立 Boost斩波电路状态空间平均模型

2.3 单区间发电机与Boost斩波型变换器非线性整体建模
在发电机每个电气周期内,二极管整流桥具有6个换相点。忽略换相续流过程,将A相和B相同时导通且电流由A相流向B相的区间称为AB区间,则每个电气周期可依次分为 AB、AC、BC、BA、CA和CB共6个区间,每个区间内的电压及电流关系见表1。

表1 不同区间内电压电流关系Tab.1 The relationship between voltages and currents in different intervals
以AB区间为例,由式(1)、式(4)和表1整理可得


由式(2)、式(3)和表1整理可得
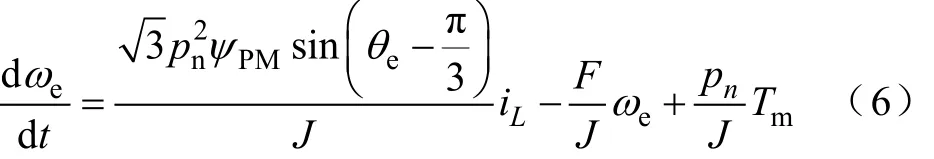
3 非线性速度控制器设计
3.1 单区间仿射非线性系统标准型
实际系统中,系统采样频率为发电机电气频率100倍以上,因此可将发电机电气角位置看作缓慢变化的常量。以AB区间为例,将发电机电气角速度和电感电流看作状态变量,以占空比为输入变量,以发电机电气角速度为输出变量,作如下变量替换

由式(5)~式(7)整理可得二阶单输入单输出仿射非线性标准型

式中

其中

当区间不同时,非线性系统(8)中参数a2和a4会产生周期性的变化,其数值见表2。
3.2 单区间输入-输出反馈线性化
以AB区间为例,采用输入-输出反馈线性化方法对系统(8)进行非线性变换。若系统能够输入-输出反馈线性化,则需满足如下条件[17]:


表2 a2和a4随区间变化数值表Tab.2 Values of variable a2 and a4 changing with intervals
对系统(8)构造向量场adfg,可得二阶方阵

由式(2),式(8)和表1可得

由于假设系统工作在连续电流模式,因此iL不等于 0;iq为定子电流中的转矩分量,在系统正常运行范围内也不等于0,由式(10)可知a4不等于0。由此可知方阵(9)对角线元素不为 0,则方阵的秩等于2,矢量场g和adfg线性无关,满足能控性条件;系统是二阶非线性系统,矢量场集合{g}满足对合性条件,因此系统可以输入-输出反馈线性化。
对输出函数h(x)进行高阶李导数递推运算可得

由上式可知系统相对阶为 2,等于系统阶数,因此原非线性系统可完全输入-输出反馈线性化。
取非线性变换


设α(x)和β(x)为中间变量,令其为
令线性系统输入变量为

经式(12)~式(14)变换,原非线性系统可转换为Brunovsky标准型

式中

由上式可知,变换后的线性系统完全能控且完全能观。
3.3 单区间线性最优控制器设计
以AB区间为例,可将系统(15)的控制问题等效为线性二次型最优跟踪器问题[18]。风力发电机一般以发电机转速作为控制目标,风电系统根据风速和输出功率等条件可得出发电机参考转速ωref,设e为转速误差,则有

可选取系统性能泛函为

式中,q2为待定系数,其计算方法参见文献[19]。
系统(15)为线性定常系统,其Riccati方程为

式中,P为对称矩阵,且由上式可解得

设λ为二阶矢量,应满足

由上式可得

输入变量v应满足

将式(19)和式(21)代入式(22)可得

将上式代入式(14)即可求得非线性系统输入变量u。
3.4 占空比限幅
实际系统中,开关信号占空比具有一定范围,设其上、下限分别为dmax和dmin,应满足

占空比上、下限的取值受功率器件最高开关频率、风电系统调速范围和系统最大开关损耗等因素的限制,对不同系统,其取值也不相同。
设d1为占空比计算的中间变量,当控制器根据式(14)计算出的u超出限幅值时,应按下式对其进行限幅

为保证系统稳定,电流iL应大于0且小于额定电流。当系统检测到iL小于电流下限imin时,为尽快增加电流应使占空比为dmax;当iL大于电流上限imax时,为尽快减小电流应使占空比为dmin。综上所述,开关信号占空比应为

在本节中非线性系统线性化及控制器设计均以AB区间为例。由表2可知,在不同区间内,式(8)中的参数a2和a4的数值会产生周期性的变化,但非线性系统方程形式、线性化过程与最优转速控制器的设计方法均相同。在不同区间切换过程中最优控制器参数q2和输入变量u的计算公式不变,只需重新计算a2和a4即可,在整体上简化了控制器的设计。
系统变换过程中涉及参数较多,当电机和外围电路选定后,其中大部分参数就已经确定,为提高运算速度,可将这部分参数预先计算后存储在微控制器内存中,系统变换时直接调用即可。
控制器结构图如图3所示。

图3 控制器结构图Fig.3 Controller diagram
表贴式永磁同步发电机定子绕组多为三相星接形式,因此采集A、B两相电流后经计算即可得到C相电流。控制器首先通过三相电流的数值及方向判断发电机的运行区间;然后根据风速等外界条件计算发电机输入机械转矩Tm,通过位置传感器计算发电机转子电气角位置θe和电气角速度ωe,通过A-D模块采集直流侧电压udc和直流侧电感电流iL;得到以上信息后,计算非线性系统状态变量x1、x2及参数a1~a7,并根据式(12)和式(13)对系统进行线性化;由转速误差计算线性系统输入v,并将其变换至非线性系统输入u,最后经限幅后得到实际占空比d,用以控制功率器件。
4 仿真与实验结果分析
将非线性控制策略和普通 PI控制策略进行了对比仿真与实验研究,仿真与实验系统参数见表3。

表3 仿真与实验系统参数Tab.3 Simulation and experiment parameters

(续)
4.1 仿真结果分析
图4为发电机不同出力情况下的系统速度响应仿真曲线。发电机开始低速运行,在3s时参考机械转速和输入机械转矩同时发生阶跃变化,条件1中ωm_ref和Tm为 130r/min和 70N·m;条件 2中ωm_ref和Tm为200r/min和120N·m;条件 3中ωm_ref和Tm为 280r/min和170N·m。

图4 动态性能对比仿真波形Fig.4 Simulation waveforms of dynamic performance
由图4可以看出,不同条件下两种控制器作用下的系统稳态运行平稳,稳态性能基本一致。PI控制器以稳态模型为基础,其动态响应速度较慢,并且随着发电机出力的增加,响应时间明显增加。非线性控制器以动态模型为基础,相同条件下,其响应速度较PI控制器有了明显的改善;此外,由于反馈线性化方法是基于模型的控制方法,随着发电机出力的增加,其控制率的计算值也随之改变,动态性能没有明显的下降,在发电机正常运行范围内保持了良好的动态特性。
4.2 稳态性能实验结果分析
为进一步研究系统特性,搭建了一套 3kVA的实验系统,该系统由一台变频器控制一台异步电机作为原动机,原动机与一台永磁同步发电机通过联轴器相连。变频器经通讯接口将原动机输出转矩信息传给Boost斩波电路微控制器,微控制器为TI公司的 TMS320F28335,内部工作频率设定为150MHz。占空比d上、下限分别设定为0.9和0.1;iL上、下限分别设定为15A和0.5A。
图5和图6是输入机械转矩为80N·m、参考机械转速分别为150r/min和250r/min时,系统稳态对比实验波形。图中,ωm为发电机机械转速,Te和Teavg分别为发电机电磁转矩及其平均值,iL和iLavg分别为电感电流及其平均值。

图5 参考机械转速150r/min稳态性能对比实验波形Fig.5 Experimental waveforms of steady-state performance when the reference mechanical speed is set to be 150r/min
由图5可以看出,稳态时两种控制器作用下的系统均能较好地跟踪参考机械转速。由于二极管整流桥的非线性特性,Te和iL均存在有规律的波动,波动频率为发电机电气频率的6倍。PI控制器作用下的Te和iL波动形状接近二极管自然换相波形,且不同转速下的波动幅度基本一致;非线性控制器由于采用了分区间控制方法,系统低速时换相续流时间相对较长,系统模型误差相对较大,因此iL波动幅度略大,但不同转速下的平均值基本相等。由图5还可看出,虽然Te存在波动,但其平均值较为平稳且Teavg与输入机械转矩基本相等,使系统能够保持稳定运行。

图6 参考机械转速250r/min稳态性能对比实验波形Fig.6 Experimental waveforms of steady-state performance when the reference mechanical speed is set to be 250r/min
由稳态性能对比实验结果可知,由于PI控制器以系统稳态数学模型为基础,因此在正常运行范围内可保持较好的稳态性能。两种控制器作用下的系统均可在正常运行范围内保持稳定,稳态转速平稳,稳态性能基本一致。
4.3 动态性能实验结果分析
图7是输入机械转矩保持不变,参考机械转速改变时,系统动态性能对比实验波形。在整个调速过程中,系统始终保持80N·m输入机械转矩不变,参考机械转速开始为 200r/min,然后向上阶跃至250r/min,2s后向下阶跃至150r/min。

图7 参考机械转速变化时动态性能对比实验波形Fig.7 Experimental waveforms of dynamic performance when the reference mechanical speed is changed
由图7可以看出,非线性控制器作用下的系统动态性能有较为明显的改善,机械转速阶跃响应较为迅速,响应时间较短,且超调较小。当参考机械转速向上跃变时,Te和iL迅速降低,使发电机转速能迅速提高;在参考机械转速向下跃变时,Te和iL迅速提高,使发电机转速能迅速降低;由于对iL进行了限幅,因此其被限制在正常运行范围内,以保证系统能稳定运行。
图8是参考机械转速保持不变,输入机械转矩改变时,系统动态性能对比实验波形。系统参考机械转速保持 200r/min不变,输入机械转矩开始为70N·m,然后向上阶跃至 100N·m,2s后向下阶跃至40N·m。
由图8可以看出,在转矩改变的时刻,由于非线性控制器作用下的Te和iL响应较为迅速,其转速波动较小。在三种情况切换过程中,非线性控制器作用下的系统可以较好地跟踪参考转速。非线性控制器由于采用了分区间控制方法,在电磁转矩较大时电流值相对较大,系统模型误差相对较大,因此iL波动幅度略大,并导致了Te波动幅度也略大,但Te平均值与输入机械转矩基本相等,使系统能够稳定运行。

图8 输入机械转矩变化时动态性能对比实验波形Fig.8 Experimental waveforms of dynamic performance when the input mechanical torque is changed
由以上分析可知,由于非线性控制器以动态模型为基础,因此在正常运行范围内,对参考转速和输入转矩阶跃响应较为迅速,可以稳定运行,动态性能改善较为明显。
5 结论
针对由表贴式永磁同步发电机、二极管整流桥和 Boost斩波电路组成的强非线性系统,分区间建立了整体非线性数学模型,并在单区间内采用输入-输出反馈线性化方法将非线性系统转换为线性系统,在此基础上设计了转速线性最优控制器。该设计方法的数学转换过程较为简单,虽然涉及较多参数,但大部分参数可以预先计算;线性最优控制器的设计理论较为成熟,系统参数整定方法较为简单,且不同区间内控制器的参数相同。经实验验证,该方法作用下的系统稳态时能较好地跟踪参考转速;动态性能提高较为明显,阶跃响应迅速,超调较小,可在正常运行范围内稳定工作,在一定程度上克服了普通PI控制器的不足。该方法对直驱式永磁同步风电系统中 Boost斩波型变换器控制策略的设计具有一定的参考价值。
[1]Xia Changliang, Song Zhanfeng. Wind energy in China: current scenario and future perspectives[J].Renewable and Sustainable Energy Reviews, 2009,13(8): 1966-1974.
[2]Zhang S, Tseng King Jet, Vilathgamuwa D M, et al.Design of a robust grid interface system for PMSG-based wind turbine generators[J]. IEEE Transactions on Industrial Electronics, 2011, 58(1):316-328.
[3]胡书举, 李建林, 许洪华. 永磁直驱风电系统变流器拓扑分析[J]. 电力自动化设备, 2008, 28(4):77-81.
Hu Shuju, Li Jianlin, Xu Honghua. Analysis of converter configuration for direct-drive wind power system with PMSG[J]. Electric Power Automation Equipment, 2008, 28(4): 77-81.
[4]Knight A M, Peters G E. Simple wind energy controller for an expanded operating range[J]. IEEE Transactions on Energy Conversion, 2005, 20(2):459-466.
[5]Amei K, Takayasu Y, Ohji T, et al. A maximum power control of wind generator system using a permanent magnet synchronous generator and a boost chopper circuit[C]. Power Conversion Conference,2002: 1447-1452.
[6]李建林, 高志刚, 赵斌, 等. 直驱型风电系统大容量 Boost PFC拓扑及控制方法[J]. 电工技术学报,2008, 23(1): 104-109.
Li Jianlin, Gao Zhigang, Zhao Bin, et al. Application of single-switch three-phase boost PFC in direct-drive wind power generation system[J]. Transactions of China Electrotechnical Society, 2008, 23(1): 104-109.
[7]Haque M E, Negnevitsky M, Muttaqi K M. A novel control strategy for a variable-speed wind turbine with a permanent-magnet synchronous generator[J].IEEE Transactions on Industry Applications, 2010,46(1): 331-339.
[8]邓卫华, 张波, 丘东元, 等. 电流连续型Boost变换器状态反馈精确线性化与非线性 PID控制研究[J].中国电机工程学报, 2004, 24(8): 45-50.
Deng Weihua, Zhang Bo, Qiu Dongyuan, et al. The research of state variable feedback linearization method on the CCM boost converter and nonlinear PID control law[J]. Proceedings of the CSEE, 2004,24(8): 45-50.
[9]严干贵, 李军徽, 蒋桂强, 等. 背靠背电压源型变流器的非线性解耦矢量控制[J]. 电工技术学报,2010, 25(5): 129-135.
Yan Gangui, Li Junhui, Jiang Guiqiang, et al.Nonlinear decoupled-vector control of back-to-back voltage source converter[J]. Transactions of China Electrotechnical Society, 2010, 25(5): 129-135.
[10]帅定新, 谢运祥, 王晓刚, 等. Boost变换器非线性电流控制方法[J]. 中国电机工程学报, 2009, 29(15):15-21.
Shuai Dingxin, Xie Yunxiang, Wang Xiaogang, et al.Nonlinear current control method for boost converter[J]. Proceedings of the CSEE, 2009, 29(15):15-21.
[11]Kim D E, Lee D C. Feedback linearization control of three-phase UPS inverter systems[J]. IEEE Transactions on Industrial Electronics, 2010, 57(3):963-968.
[12]宋文超, 林飞, 张春朋. 基于定子磁链模型的异步电动机反馈线性化控制[J]. 电工技术学报, 2003,18(4): 85-88.
Song Wenchao, Lin Fei, Zhang Chunpeng. Direct feedback linearization control of induction motors based on stator flux model[J]. Transactions of China Electrotechnical Society, 2003, 18(4): 85-88.
[13]张纯明, 郭庆鼎. 基于反馈线性化的交流直线永磁同步伺服电动机速度跟踪控制[J]. 电工技术学报,2003, 18(3): 5-9.
Zhang Chunming, Guo Qingding. Feedback linearization based control of speed tracking for AC linear permanent magnet synchronous servo motor[J].Transactions of China Electrotechnical Society, 2003,18(3): 5-9.
[14]Liutanakul P, Pierfederici S, Meibody Tabar F.Application of SMC with I/O feedback linearization to the control of the cascade controlled-rectifier/inverter-motor drive system with small DC-link capacitor[J]. IEEE Transactions on Power Electronics,2008, 23(5): 2489-2499.
[15]Matas J, Castilla M, Guerrero J M, et al. Feedback linearization of direct-drive synchronous wind-turbines via a sliding mode approach[J]. IEEE Transactions on Power Electronics, 2008, 23(3):1093-1103.
[16]Middlebrook R D, Cuk S. A general unified approach to modeling switching-converter power stages[J].International Journal of Electronics, 1977, 42(6):521-550.
[17]Slotine J J E, Li W. Applied nonlinear control[M].New Jersey: Prentice-Hall, 1991.
[18]刘豹. 现代控制理论[M]. 2版.北京: 机械工业出版社, 2000.
[19]卢强, 孙元章. 电力系统非线性控制[M]. 北京: 科学出版社, 1993.

