用于提高级联型电源系统稳定性的自适应有源电容变换器

张 欣 阮新波,2

（1. 南京航空航天大学航空电源航空科技重点实验室 南京 210016 2. 华中科技大学电气与电子工程学院 武汉 430074）

1 引言

随着电力电子技术在工农业生产、国防、环保等领域的应用范围日益扩大，人们要求电力电子产品成本低，研发周期短，能够满足快速变化的市场和客户需求。然而，目前电力电子产品的开发大多是根据客户的不同用途和要求进行特殊设计的，即所谓客户定制。该方式往往开发周期长、成本高，在开发过程中进行了大量的重复性劳动，劳动效率低，因此限制了电力电子产品生产成本的进一步降低和可靠性的进一步提高。国际电力电子学界普遍认为，解决上述问题的方法之一是电力电子系统集成[1-3]。

电力电子系统集成可以分为三个层次。第一层次是分立的元器件级集成，包括有源器件集成和无源元件集成；第二层次是模块级集成，它是将各种集成好的有源器件或无源元件集成起来，构成通用性较强的标准化变换器模块；第三层次是系统级集成，是将各种标准化变换器模块集成为满足不同需求的各种电力电子系统。

级联型系统是系统级集成中，标准化变换器模块的一种经典组合方式[4]。如图 1所示，电源到负载之间引入了多级功率变换，定义前级变换器为源变换器，后级变换器为负载变换器。该结构的优点在于：①由于引入了中间直流母线，负载变换器可以尽可能放置在负载附近，负载电压调节精度高，动态响应速度快；②直流母线电压可以适当提高，以减小由于线路阻抗引起的分布损耗，提升系统总的变换效率；③级联结构也适用于输入电压宽范围的场合。级联型系统的问题在于尽管源变换器和负载变换器单独工作是稳定的，但两者组成系统时可能不稳定[5]。因此，级联型系统的稳定性一直是人们研究的热点之一。

图1 级联型电源系统Fig.1 Cascaded power supply system

1976年，Middlebrook教授证明了源变换器输出阻抗和负载变换器输入阻抗之比可以等效为级联型系统的环路增益来判断系统的稳定性，由此提出，如果源变换器输出阻抗的模在全频率范围内小于负载变换器输入阻抗的模，则两者级联后可以确保系统稳定[5]，这就是著名的 Middlebrook判据。Middlebrook判据的条件非常严格，根据这个判据会导致整个系统的设计过于保守。为了解决这一问题，1995年，Wildrick提出了禁止区域的概念，指出只要确保源变换器输出阻抗和负载变换器输入阻抗之比的幅相曲线不包围s平面的（-1，j0）点，级联型系统就能够稳定[6]。文献[7-10]在文献[6]的基础上，对于多模块系统，给出了每个负载模块输入阻抗的设计标准，使得整个系统的设计简化到每个负载模块的独立设计上。

其实，Middlebrook判据和禁止区域的概念在本质上是一致的，即：系统的阻抗比必须满足奈奎斯特判据，才可以保证级联型系统的稳定。因此，可以直接将阻抗比是否满足奈奎斯特判据作为系统稳定的唯一标准。

基于 Middlebrook判据和禁止区域的概念，人们提出了许多解决级联型系统的稳定性问题的方法。

文献[11-13]分析了电路参数及控制方法与输入输出阻抗之间的关系，简单明了地阐述了变换器的阻抗特性，为变换器的稳定性设计提供了理论和数学依据。

文献[14]提出了在中间直流母线上串入解耦滤波器的方法。该滤波器的输入阻抗高于源变换器的输出阻抗，而其输出阻抗则低于负载变换器的输入阻抗。从而保证系统稳定。该方案只需检测前后级变换器的阻抗特性，而不需要了解电路的内部结构，因此通用性强。可是该方法存在以下不足：①滤波器的输入输出阻抗很难满足要求；②滤波器所需电容容量较大[15]，一般采用电解电容，因此降低了系统的使用寿命和功率密度；③滤波器串接于主功率回路，带来了额外的损耗。

文献[16-17]从控制上解决了稳定性问题，克服了解耦滤波器的不足，该方案从控制上减小源变换器的输出阻抗的幅值，避免和负载变换器输入阻抗交接，保证系统稳定，但需要采样源变换器的电感电流，因此通用性不强。另外，该方案会使源变换器的带宽降低，降低了源变换器的动态特性[17]。

本文提出一种解决级联型系统不稳定问题的通用解决方案，它在中间直流母线上并联一个等效为可变滤波电容的自适应稳定模块，即有源电容变换器，从而有效解决了系统的不稳定问题。该方案克服了解耦滤波器的不足，同时具有通用性。

本文首先分析级联型系统不稳定问题的原因，然后以此为基础提出有源电容变换器的概念。接着详细分析有源电容变换器的工作原理和设计准则，该变换器结构和控制不随系统电路的改变而改变，具有通用性，它不但从本质上解决了系统的稳定性问题，还可以根据系统的不稳定程度，合理有效的调节等效电容大小，降低自身损耗，具有自适应功能。最后以一个120W的级联型系统为例，给出了有源电容变换器的设计过程，并进行了实验验证。

2 有源电容变换器

2.1 级联型系统的稳定性

如图1所示，对源变换器而言，当采用电压型控制时，其闭环输出阻抗表达式为[18]

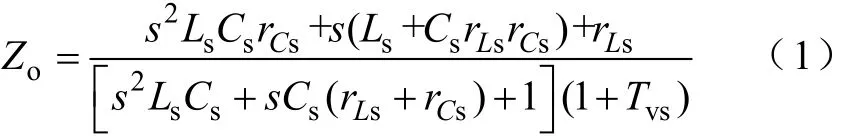
式中，对于Buck、Boost和Buck-Boost变换器，Ls和Cs分别为其电感和电容，rLs和rCs分别为电感和电容的寄生电阻，Tvs为源变换器电压环路增益。

从式（1）可以得到，源变换器的闭环输出阻抗在电压环路增益的截止频率fcs处有峰值

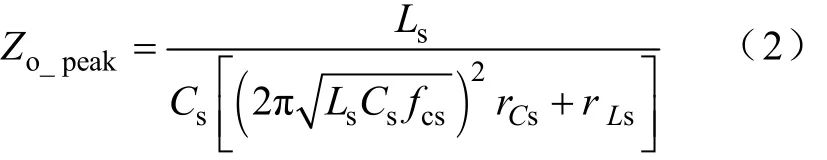
对于负载变换器而言，其输入阻抗的表达式为[5]

式中，对于 Buck、Boost和 Buck-Boost变换器，L和C分别为其电感和电容，rL和rC分别为电感和电容的寄生电阻，M为变换器的电压传输比，对于Buck、Boost和Buck-Boost变换器，M分别等于D、1/（1-D）和D/（1-D），RLd为负载电阻，Tv为负载变换器电压环路增益。

在电压环路增益截止频率fc_load内，v1T≫ ，由式（3）可得式（4），此时，输入阻抗呈现负阻特性。

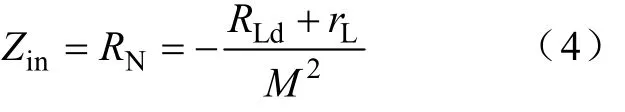
级联型系统源变换器输出阻抗和负载变换器输入阻抗之比的函数表达式为

则Tm的幅值和相角的表达式分别为

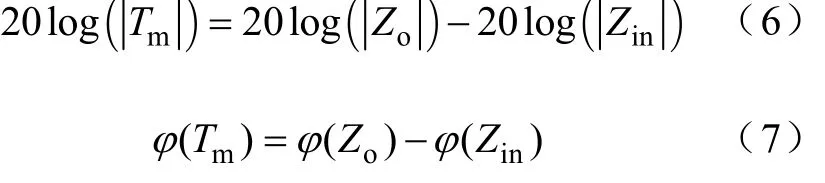
当Zo的幅值小于Zin的幅值时，系统是稳定的。当Zo和Zin幅值交接时，有两种情况，如图2所示：①阻抗交接频率低于fc_load或在fc_load附近；②阻抗交接频率高于fc_load[19]。

对于第一种情况，由于Zin的负阻特性，φ（Tm）的相位裕度小于0，系统不稳定。对于第二种情况，在任何条件下，φ（Tm）的相位裕度都大于0，系统稳定。因此，级联型系统不稳定问题的原因为：源变换器输出阻抗的峰值在负载变换器电压环路增益的截止频率内或附近和负载变换器的输入阻抗交接，此时系统相位裕度小于0，导致系统不稳定。

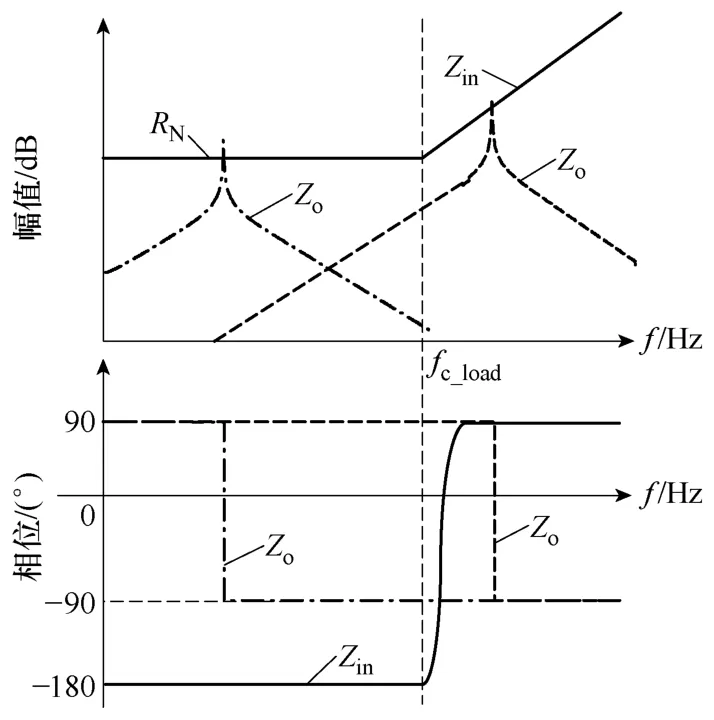
图2 系统不稳定时的阻抗示意图Fig.2 Characteristics of Zo and Zin for Instability system

2.2 有源电容变换器

由式（2）可得，源变换器输出阻抗的峰值与其输出电容大小成反比，因此增加源变换器的输出电容可以减小其输出阻抗峰值，避免和负载变换器输入阻抗交接，从而保证系统稳定。

保证系统稳定所需电容的容值较大，一般是在直流母线上并电解电容，如图3所示。但是电解电容的引入从可靠性角度考虑，降低了系统的使用寿命；从系统集成的角度考虑，属于第一层次分立元件的集成，不满足系统集成的要求。

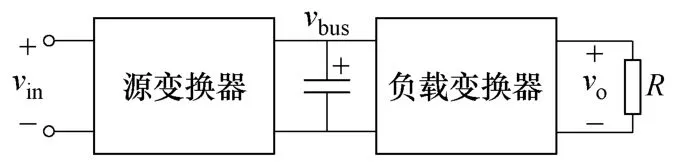
图3 采用电解电容保证级联型系统稳定Fig.3 Cascaded system with electrolytic capacitor

本文利用文献[20]的概念，提出了有源电容变换器的概念，即通过一个不含电解电容的变换器，实时为系统提供保持稳定所需的等效电容电流。该变换器并联在直流母线上，如图4所示。图5给出了有源电容变换器的主电路结构图，其本质为一个Buck/Boost双向变换器，由开关管Qa1和Qa2、电感La和电容Ca组成。

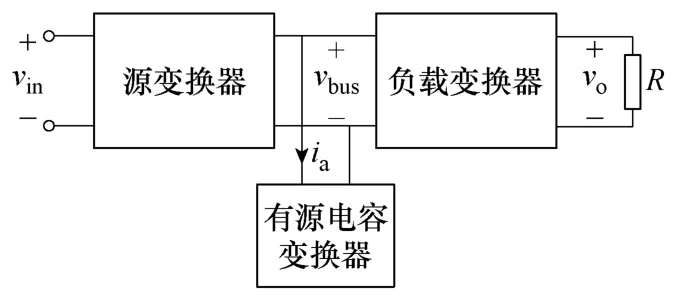
图4 采用有源电容变换器的级联型系统Fig.4 Cascaded system with active capacitor converter

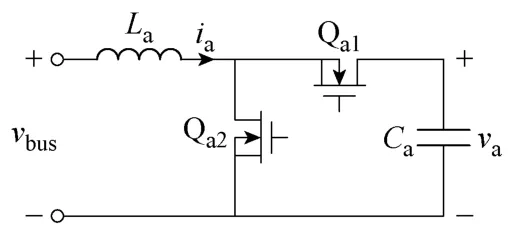
图5 有源电容变换器主电路Fig.5 Main circuit of active capacitor converter

有源电容变换器的控制框图如图6所示，工作原理如下：首先通过检测vbus，根据系统的振荡程度，给出变换器需要向母线注入的等效电容电流大小，作为ia的基准，确保变换器的自适应电容特性（该部分电路在3.2节有详细讨论）。同时，检测变换器Ca电压的大小，通过调节器G1（s）保证va稳定，确保变换器正常工作。

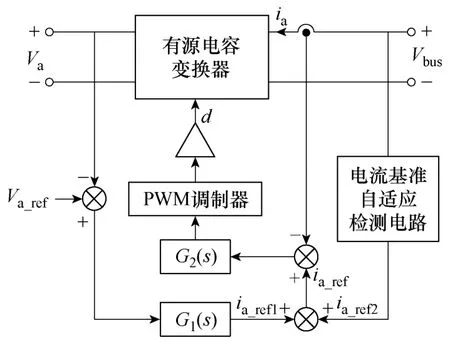
图6 有源电容变换器控制框图Fig.6 Control strategy of active capacitor converter

下面具体介绍有源电容变换器的参数设计和控制实现。

3 有源电容变换器的设计

3.1 主电路及其参数确定

有源电容变换器的功能是在直流母线上增加调节系统稳定的等效电容，首先确定该电容的大小，为了便于说明，等效电容用Ce表示。

如图2所示，当源变换器的输出阻抗峰值小于负载变换器输入阻抗时，系统稳定。根据文献[21]可知，考虑到实际电路参数变化给阻抗带来的影响，在源变换器输出阻抗和负载变换器输入阻抗之间引入6dB的稳定裕度，即

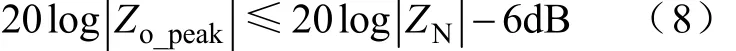
结合式（2）和式（3）可得，系统满足式（8）所需的母线电容表达式为

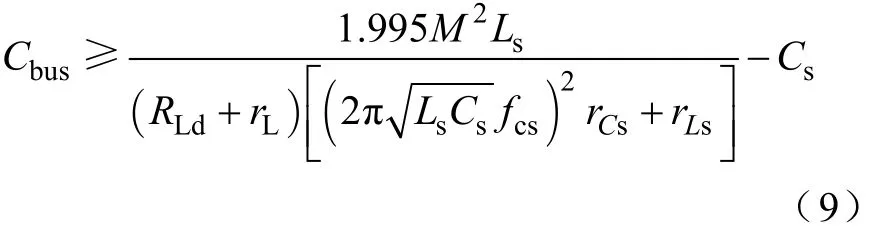
对于有源电容变换器而言，其等效电容越大，变换器所要提供的无功功率越多，损耗和成本也相应增加，因此可选取Ce=Cbus_min。

如图4所示，定义直流母线电压vbus为

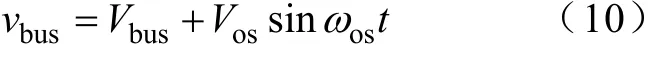
式中，Vbus和Vos分别为直流母线电压的直流分量和交流分量,一般要求Vos≤1%Vbus[22]；ωos为系统的振荡角频率，ωos=2πfos=2πfcs[5]。

根据式（10），可得有源电容变换器端口电流ia为

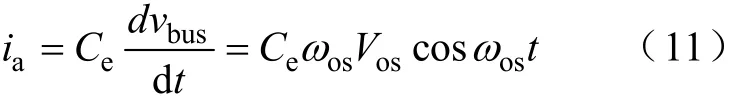
由式（10）和式（11）可以推出有源电容变换器的瞬时功率pa为

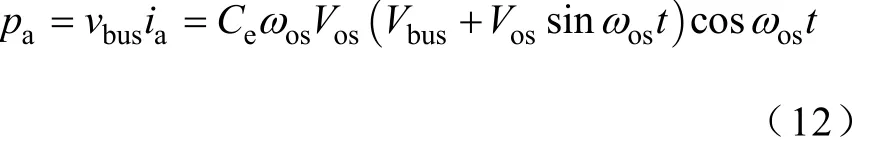
考虑到，系统稳态工作时，Vos和Vbus相比可以忽略，因此，图7给出了有源电容变换器工作时的输出端口电压，电流和功率波形。

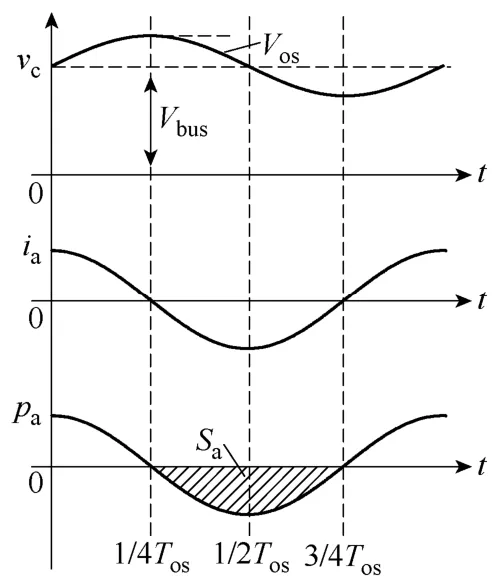
图7 有源电容变换器端口电压电流和功率示意图Fig.7 Voltage, current and power pulsation waveforms of active capacitor converter

因此，有源电容变换器半个周期内提供的能量为

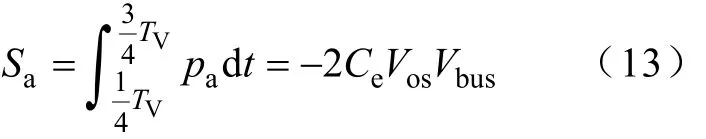
3.1.1 开关管的选择

图5所示，当Qa1导通，Qa2关断时，ia在Δt时间内的增加量为

当Qa1关断，Qa2导通时，ia在Δt时间内的减少量为

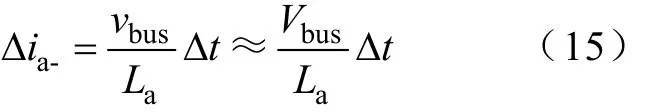
因此，Ca电压va影响ia的变化率，va越大，ia变化越快，电感电流的跟踪效果越好。但是va增加会导致 Qa1和 Qa2的电压应力增加，因此可选择Va=2Vbus，这样ia相同时间内的电流变化量相等，既保证了电感电流的跟踪效果，又考虑了开关管的电压应力。

开关管 Qa1和 Qa2的电压应力为Va，电流应力为ia的幅值，如式（16）所示。

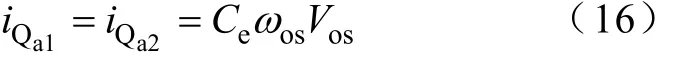
因为Ce和负载的大小成正比。所以，满载时，有Qa1和Qa2的最大电流应力

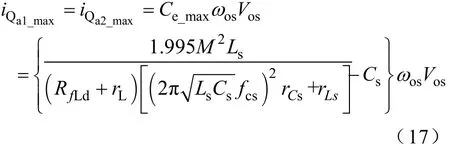
式中，RfLd为满载时的负载电阻。

结合Va和式（17）可选择合适的开关管。

3.1.2Ca的确定

有源电容变换器中Ca提供能量的表达式为

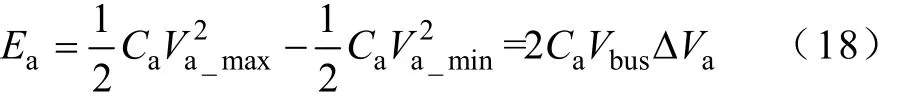
式中，ΔVa为va的脉动值，取va的10%

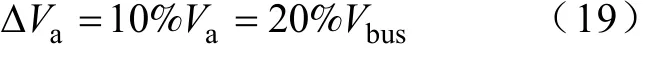
Ca按照系统满载时设计，结合式（13）、式（18）和式（19）可得Ca表达式为

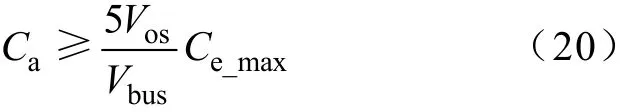
实际电路中希望避免使用电解电容，以保证系统的使用寿命，从而选取Ca=Ca_min，Ca采用薄膜电容。

3.1.3 开关频率fs和La的确定

ia对基准的跟踪效果决定了有源电容变换器的性能好坏。而这与有源电容变换器的开关频率及La大小密切相关。

ia是一个频率为fos的交流电流。为了保证良好的跟踪效果，有源电容变换器的开关频率至少大于基准电流频率的十倍，即

为了保证电流的跟踪效果，本文定义电感电流一个周期内允许的最大脉动不超过基准电流峰值的20%。从而可得La的表达式为

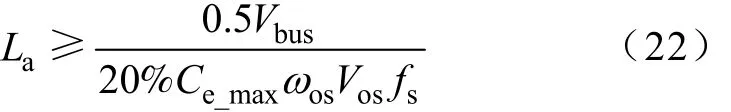
考虑到La越大，ia变化率越小，因此La取其最小值。

3.2 自适应控制电路实现

2.2节简要的讨论了有源电容变换器的工作原理。该电路控制的难点在于，ia的基准电流和系统负载成正比（由式（9）和式（11）可知）。为此本文对有源电容变换器提出了自适应控制策略。图 8给出了其自适应实现电路。下面讨论其工作原理。

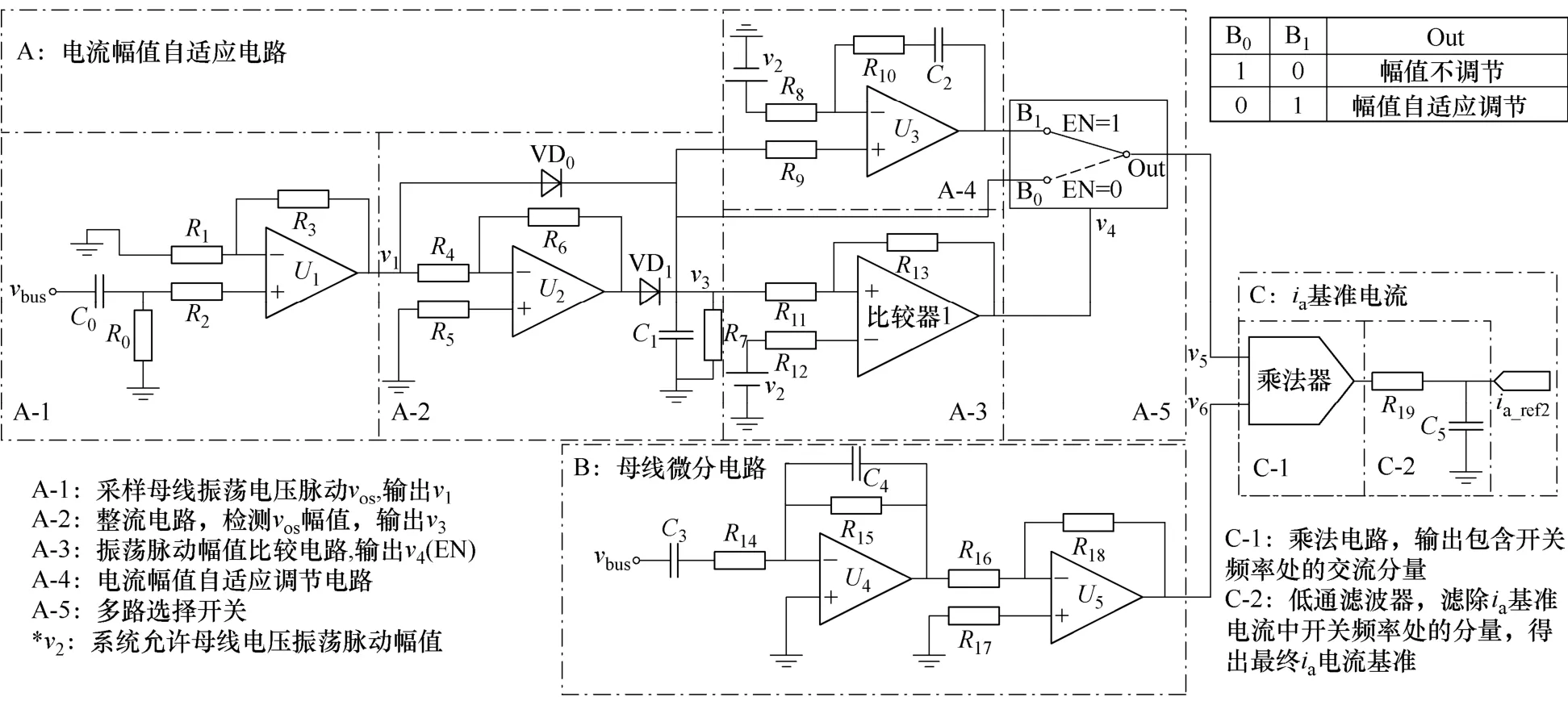
图8 自适应电路图Fig.8 Circuit for adaptive control

图8电路主要由三个部分组成，A电路决定了ia基准电流幅值；B电路决定了ia基准电流的特性；C电路决定了最终的ia基准电流基准。

A电路目的是根据系统振荡情况，自动调节ia电流幅值大小，保证系统稳定的同时，减少自身的导通损耗，实现自适应功能。

它首先检测vbus，通过高通滤波器C0和R0，滤除直流分量，采得vbus振荡频率处的交流分量vos（v1）。接着通过整流电路将vos整成直流脉动量，经过C1，R7得到vos的交流幅值v3。定义系统允许的交流幅值为v2，当v3＜v2时，选通开关的使能信号 EN=0，Bo导通，ia不参与调节，v3保持不变；当v3＞v2时，选通开关的使能信号EN=1，B1导通，ia参与调节，原理如下。负载重时，vos大，v3增加，A-4电路电流幅值自适应调节电路输出上升，ia_ref2的幅值v5增加，有源电容变换等效的电容容量增加，系统稳定；负载轻时，vos小，v3减小，A-4电路电流幅值自适应调节电路输出下降，ia_ref2的幅值v5减小，有源电容变换等效的电容容量减小，保证系统稳定的同时减小ia电流大小，减小有源电容变换器损耗。ia的幅值自适应调节。

B电路为实用微分电路[23]，对vbus微分，保证了ia为电容电流特性，输出为v6。

C电路先经过一个乘法电路，乘法器输入为v5和v6，乘法器输出既包括了系统振荡频率处的交流量，即有源电容变换器的等效电容电流，还包含了系统变换器开关频率处的交流量。最后通过低通滤波器C5和R19，滤除其中开关频率处的交流量。该输出即是式（11）所示的ia基准电流。

4 设计实例

在上述分析的基础上，以源变换器（50 kHz）和负载变换器（100 kHz）都是Buck变换器的120W级联型系统为例（图8），设计有源电容变换器，如图9所示。表给出了其具体电路参数。

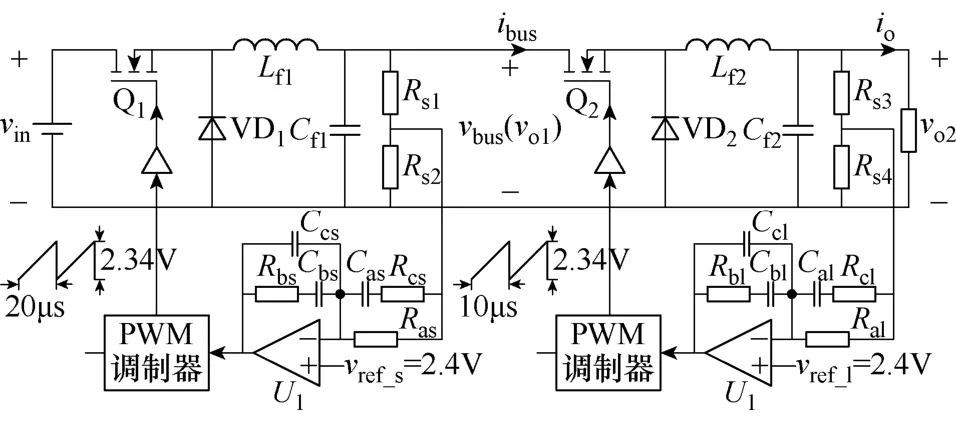
图9 级联型系统Fig.9 Cascaded system

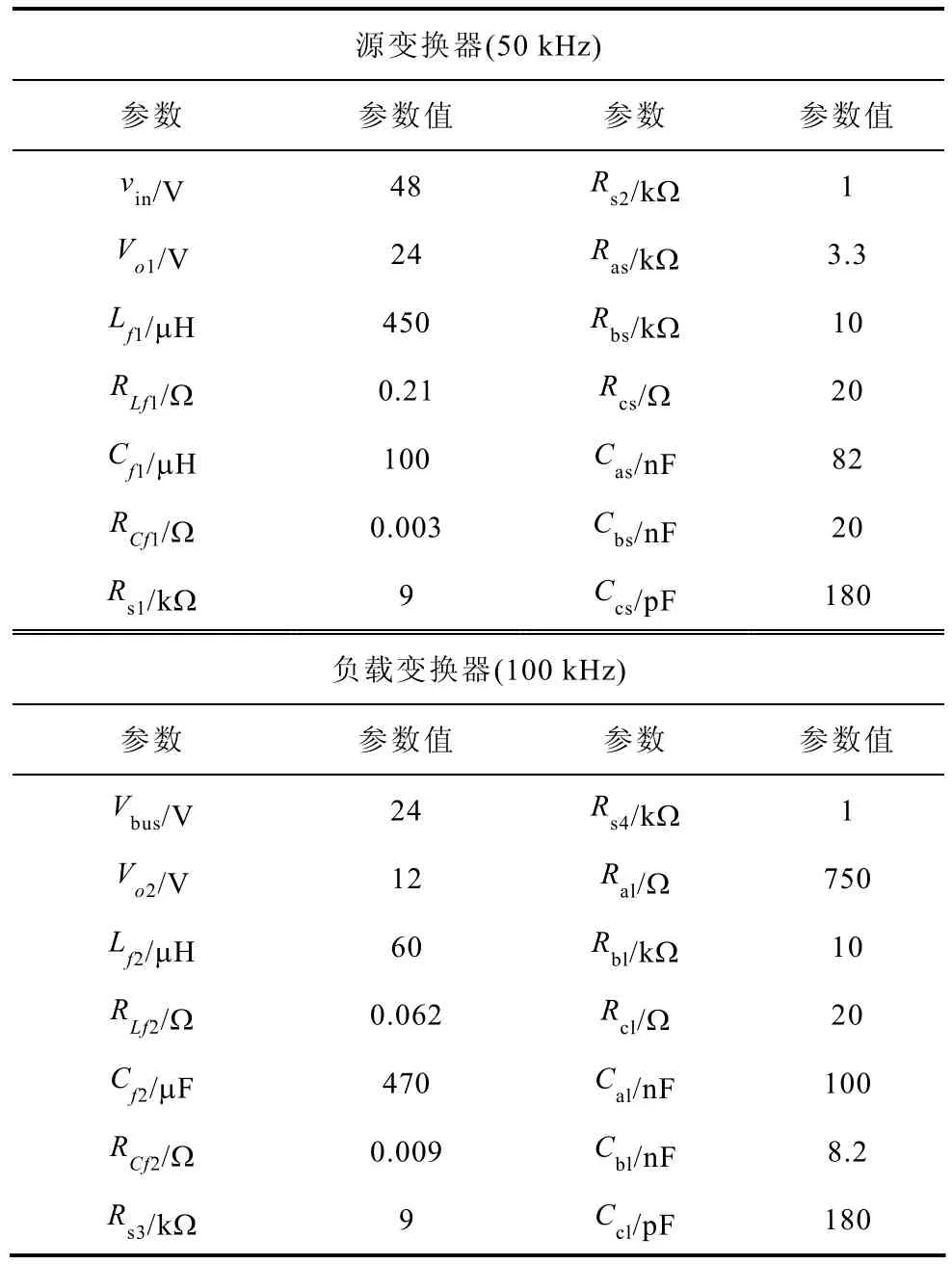
表 源变换器与负载变换器主电路参数和控制电路参数Tab. Parameters of source converter and load converter’s circuits

图10 给出了不同负载时系统阻抗伯德图：满载和半载时，源变换器输出阻抗和负载变换器输入阻抗交接，交接频率在900Hz左右，因此满载和半载时，系统级联会出现900Hz振荡；轻载（1/4载）时，源变换器输出阻抗和负载变换器输入阻抗不交接，系统稳定。

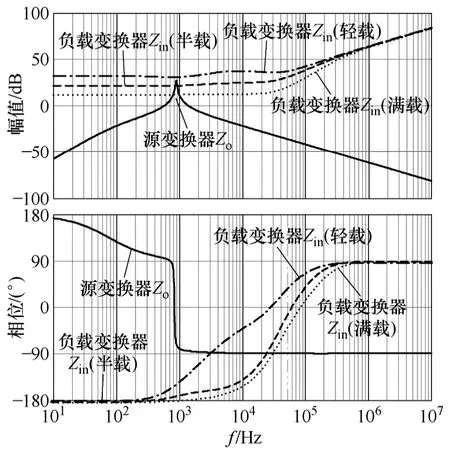
图10 系统不同负载时，Zo和Zin的幅相特性Fig.10 Zo and Zin for Fig 11’s system at different load

由式（9）可得，负载不同，所需要的等效电容大小也不同。由3.1节的分析可知，满载时所需等效电容最大。根据表和式（9），可得120W时等效电容大小为Ce_max=2057μF，这里取Ce_max=2200μF。

由式（11），图9和表得，ia=2.98cos（5652t），电流幅值为3A。由3.1节的分析和表得，va=48V。因此，Qa1和Qa2的电压电流应力分别为：48V和3A。为了降低导通损耗，选取IXYS公司的IXKP20 N60C5M（7A/600V）。

由式（20）可得Ca取110μF。可用100V/110μF薄膜电容[24]。

考虑电感的跟踪效果和体积，由式（21）和式（22）可得，开关频率取50 kHz，La取900μH。

5 实验验证

图11给出了源变换器和负载变换器满载单独工作时的实验波形，可见，两者单独工作时稳定。

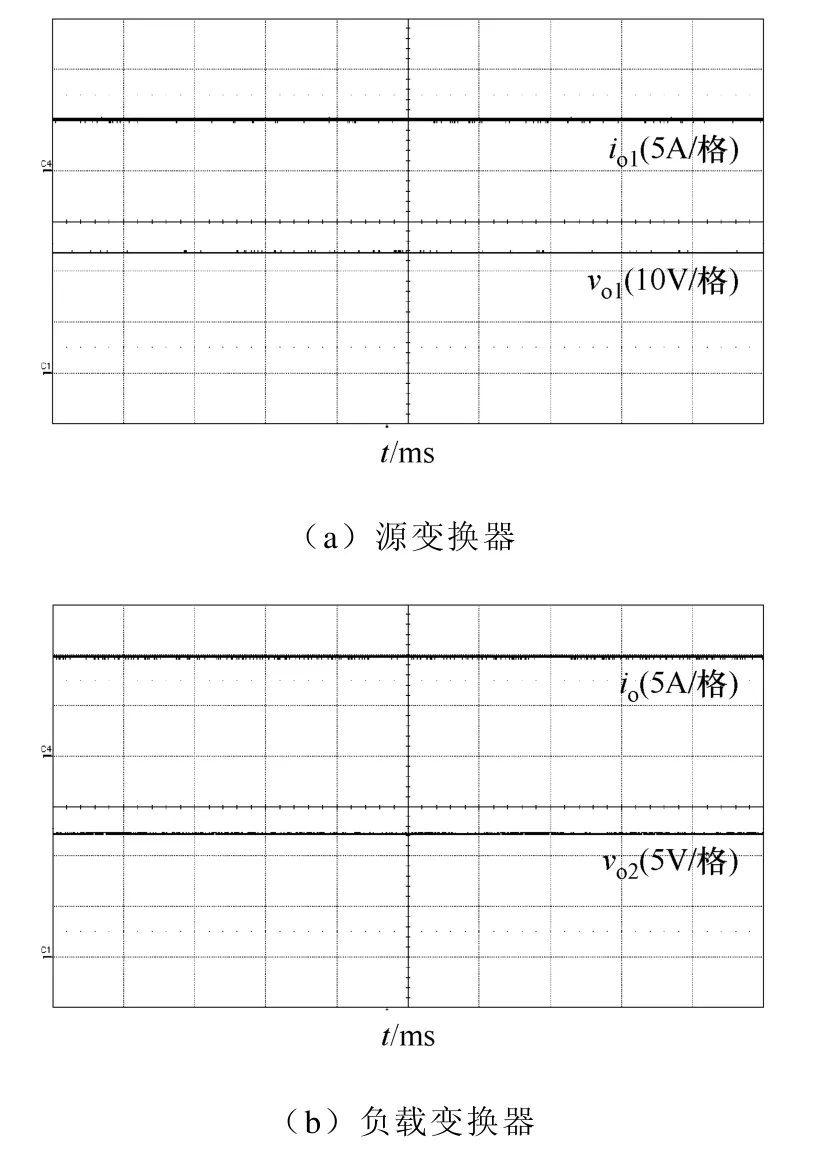
图11 源变换器和负载变换器独立工作实验波形Fig.11 Experimental waveforms of source and load converter when they work independently

图 12～图 14分别给出了不同负载条件下，系统增加有源电容变换器前后的实验波形，图中从上到下依次为负载电流io，母线电压vbus，系统输出电压 vo2。

图12给出了满载时，加有源电容变换器前后系统的中间母线电压和输出电压的交流分量波形。从图12a可以看出，加有源电容变换器之前，中间母线电压和输出电压存在振荡现象，振荡频率约为900Hz，在阻抗交接频率范围以内，因此该振荡是系统阻抗不匹配引起的。从图12b可以看出，加有源电容变换器之后，中间母线电压和输出电压均没有振荡，说明有源电容变换器有效解决了系统满载时的稳定性问题。

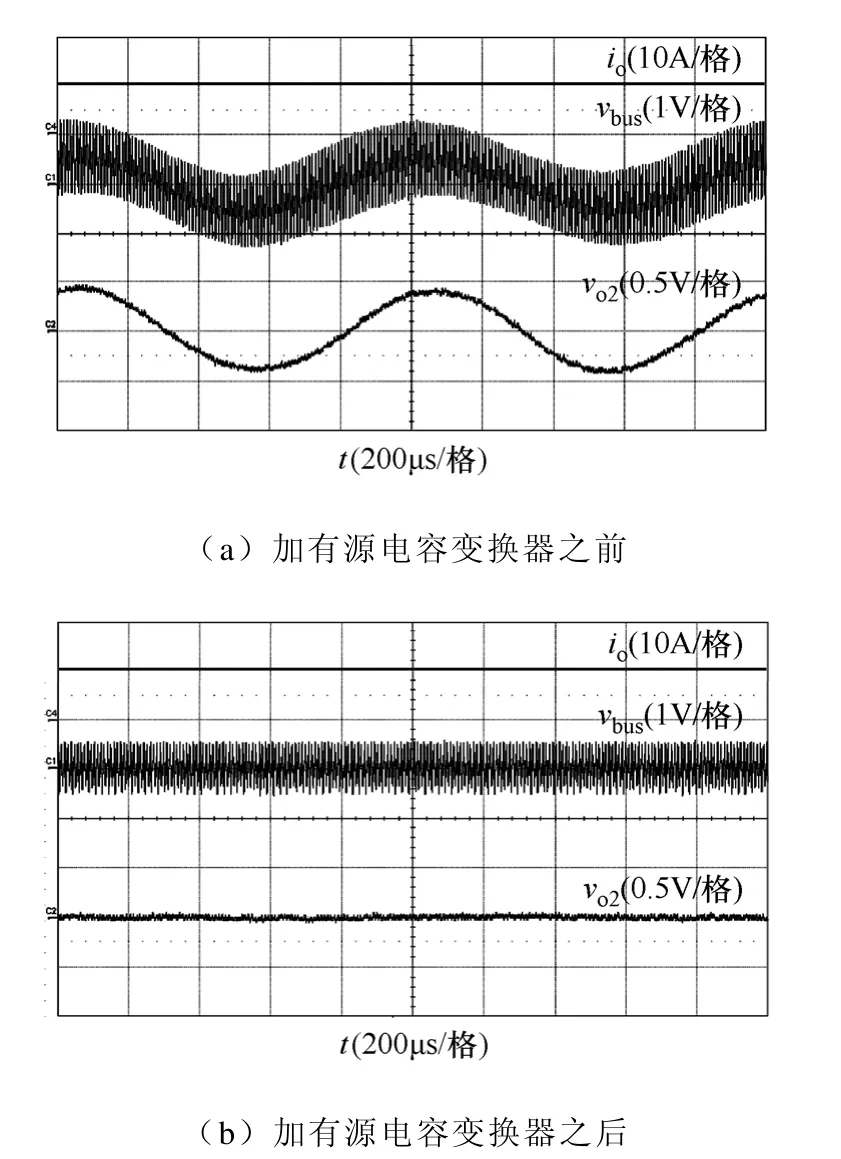
图12 加有源电容变换器前后满载时的实验波形Fib.12 Experimental waveforms of cascaded system at full load

图13给出了半载时，加有源电容变换器前后的中间母线电压和输出电压的交流分量波形。从图13a可以看出，加有源电容变换器之前，中间母线电压和输出电压存在振荡现象，该振荡频率约为900Hz，振荡程度比满载时要小。从图 13b可以看出，加有源电容变换器之后，中间母线电压和输出电压均没有振荡，说明有源电容变换器有效解决了系统半载时的稳定性问题。

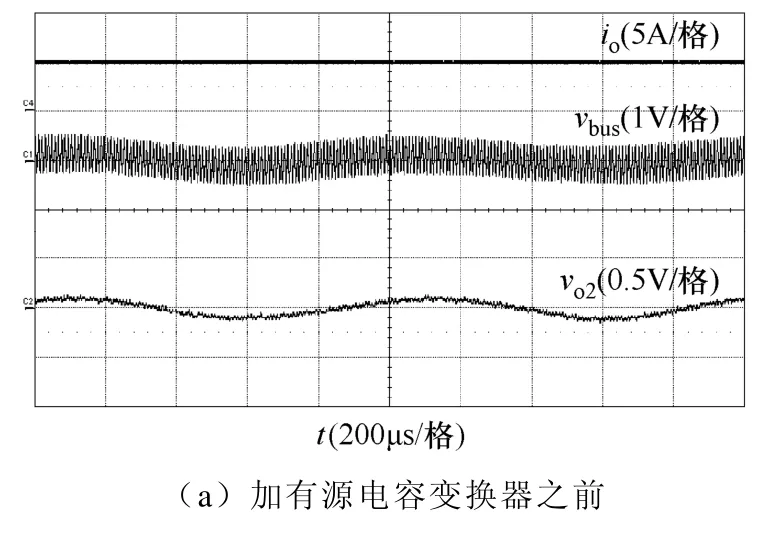
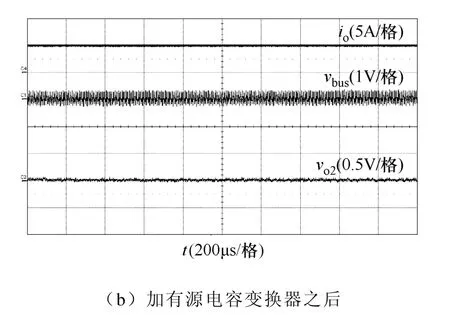
图13 加有源电容变换器前后半载时的实验波形Fig13. Experimental waveforms of cascaded system a half load

图14给出了轻载（1/4载）时，加有源电容变换器前后的中间母线电压和输出电压的交流分量波形。从图14a可以看出，加有源电容变换器之前，系统稳定，这和图9的分析一致；从图14b可以看出，加有源电容变换器之后，系统仍然稳定。

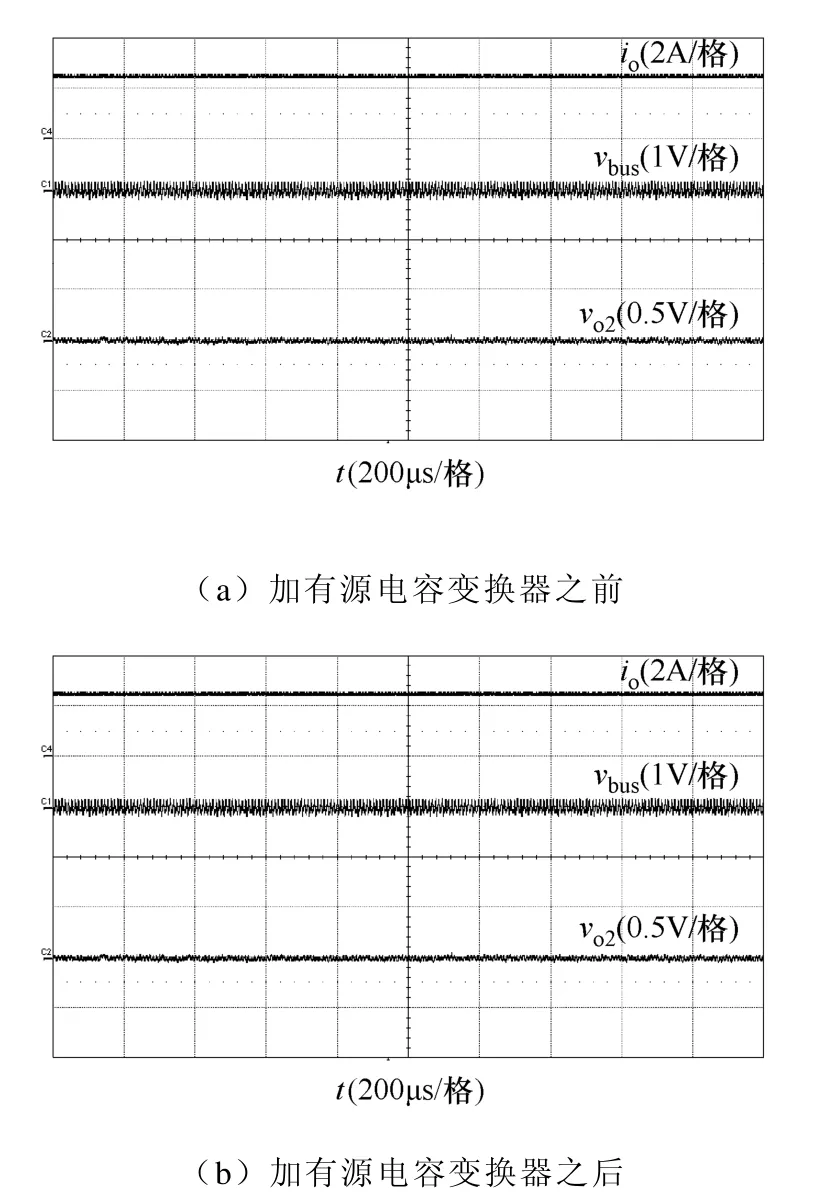
图14 加有源电容变换器前后轻载(1/4载)时的实验波形Fib.14 Experimental waveforms of cascaded system at light load

图 15给出了有源电容变换器不同负载时，Ca电压波形va，La基准电流和实际电流波形，说明有源电容变换器工作正常。不同负载条件下，有源电容变换器辅助电感电流不同，这和式（11）的分析相一致。

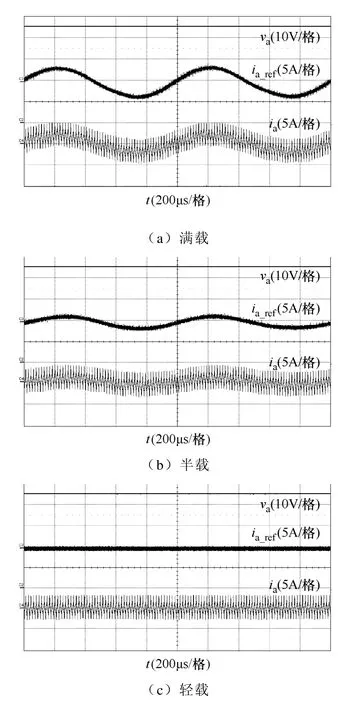
图15 有源电容变换器ia_ref，ia和va波形Fig.15 Waveforms of ia_ref，ia and va of active capacitor converter

图 16给出系统负载在半载和满载之间跳变时负载电流、有源电容变换器电感基准电流及电感电流波形。图16说明有源电容变换器可以随着负载变化，自适应的调节电感电流大小，并且可以正常稳定工作。

图16 半载-满载-半载时，io，ia_ref和ia实验波形Fig.16 Waveforms of ia_ref，ia and va of active capacitor converter when the load step between full load and 50% full-load

上述实验和理论分析一致，证明本文所提有源电容变换器不但可以有效地解决系统不稳定问题，还具有自适应性。

6 结论

本文从系统的角度分析了级联型系统不稳定问题的原因：源变换器输出阻抗的峰值在负载变换器电压环路增益的截止频率以内或附近和负载变换器的输入阻抗交接，引起系统相位裕度小于 0，导致不稳。针对这个问题，本文提出了有源电容变换器，既等效地增加了源变换器的输出电容大小，避免了源变换器输出阻抗和负载变换器输入阻抗的交接，还没有引入电解电容，不影响系统的使用寿命。本文详细的介绍了有源电容变换器的电路拓扑，给出了变换器主电路参数的设计准则，同时针对不同负载条件下所需等效电容值不同的特点，提出了有源电容变换器的自适应控制策略。最后以一个120W，48V-24V-12V的级联型不稳定系统为例，设计了有源电容变换器，并进行了实验验证，实验结果表明，有源电容变换器不但可以解决系统的稳定性问题，还具有良好的自适应特性，在级联型供电系统中具有良好的实用价值和应用前景。

[1]钱照明, 张军明, 谢小高, 等. 电力电子系统集成研究进展与现状. 电工技术学报, 2006, 21(3): 1-14.

Qian Zhaoming, Zhang Junming, Xie Xiaogao, et al.Progress in Power Eleetronic System Integration[J].Transactions of China Electrotechrical Society, 2006,21(3): 1-14.

[2]Van Wyk J D, Lee F C. Power electronics technology-Status and future[C]. Proceedings of the IEEE Industry Applications Conference, 1999, 61-70.

[3]Blaabjerg F, Consoli A, Ferreira J A, et al. The future of electronic power processing and conversion[J].IEEE Transactions on Power Electronics, 2005, 20(3):715-720.

[4]Luo S. A review of distributed power systems part I:DC distributed power system[J]. Proceedings of the IEEE Aerospace and Electronic Systems Magazine,2005, 20(8): 5-16.

[5]Middlebrook R D. Input filter considerations in design and application of switching regulators[C].Proceedings of the IEEE Industry Applications Conference, 1979: 366-382.

[6]Wildrick C M, Lee F C, Cho B H, et al. A method of defining the load impedance specification for a stable distributed power system[J]. IEEE Transactions.Power Electronics, 1995, 10(3): 280-285.

[7]Feng X, Ye Z, Xing K, et al. Individual load impedance specification for a stable dc distributed power system[C]. Proceedings of the IEEE Applied Power Electronics Conference, 1999: 923-929.

[8]Feng X, Ye Z, Xing K, et al. Impedance specification and impedance improvement for dc distributed power system[C]. Proceedings of the IEEE Power Electronics Specialist Conference, 1999: 889-894.

[9]Feng X, Liu J, Lee F C. impedance specifications for stable dc distributed power system[J]. IEEE Transactions on. Power Electronics, 2002, 17(2): 157-162.

[10]Chen Y, Feng X, Lee F C. System stability analysis based on three-dimension forbidden region[C].Proceedings of the IEEE Industry Applications Conference, 1999: 1-4.

[11]Abe S, Hirokawa M, Zaitsu T, et al. Optimal bus capacitance design for system stability in onboard distributed power architecture[C]. Proceedings of the International Symposium on Power Electronics,Eleetrical Drives, Automation and Motion, 2008:393-399.

[12]Abe S, Hirokawa M, Zaitsu T, et al. Stability comparison of voltage mode and peak current mode control for bus converter in on-board distributed power system[C]. Proceedings of the International Telecommunications Energy Conference, 2006: 1-5.

[13]Wu Tao, Ruan Xinbo. Characterization of input/output impedance specifications for dc distributed power system[C]. Proceedings of the International Telecommunications Energy Conference,2006: 982-987.

[14]Choi B, Cho B H. Intermediate line filter design to meet both impedance compatibility and EMI specifications[J]. IEEE Transactions on. Power Electronics, 1995, 10(5): 583-589.

[15]R. Erickson. Optimal single-resistor damping of input filter[C], Proceedings of the IEEE Applied Power Electronics Conference, 1999: 1073-1097.

[16]Karppanen M, Hankaniemi M, Suntio T. Dynamical characterization of peak-current-mode- controlled buck converter With output-current feedforward[J].IEEE Transactions on Power Electronics, 2007, 22(2):451.

[17]Rahimi A M. Emadi A. Active damping in dc/dc power electronic converters: a novel method to overcome the problems of constant power loads[J].IEEE Transactions on Industrial Electronics, 2009,56(5): 1428-1439.

[18]Abe S, Hirokawa M, Zaitsu T, et al. Stability.design consideration for on-board distributed power system consisting of full-regulated bus converter and POLs[C]. Proceedings of the IEEE Power Electronics Specialist Conference, 2006: 2669-2673.

[19]Abe S, Hirokawa M, Zaitsu T, et al. Stability.design consideration of full-regulated bus converter for system stability of on-board distributed power system[C]. Proceedings of the International Symposium on Power Electronics, Eleetrical Drives,Automation and Motion, 2006: 11-15.

[20]Shinjo, F, Wada, K, Shimizu T A Single-phase grid-connected inverter with a power decoupling function[C]. Proceedings of the IEEE Power Electronics Specialist Conference, 2007: 1245-1249.

[21]Wildrick C M. Stability of distributed power supply system[D], Blacksburg: Virginia Polytechnic.Institute. State University, 1993.

[22]阮新波, 严仰光, 脉宽调制DC/DC全桥变换器的软开关技术[M], 科学出版社, 1999.

[23]康华光. 电子技术基础(模拟部分)[M]. 北京: 高等教育出版社, 2005.

[24]http://www.esmchina.com/ART_8800060235_1500_2 701_3606_0_91464a8d.HTM.